CS 473 Algorithms I Lecture X 1 Properties

CS 473 -Algorithms I Lecture X 1 Properties of Ranks CS 473 Lecture X 1

Analysis Of Union By Rank With Path Compression When we use both union-by-rank and path-compression the worst case running time is O(mα(m, n)) where α(m, n) is the very slowly growing inverse of the Ackerman’s function. In any conceivable application of disjoint-set data structure α(m, n) ≤ 4. Thus, we can view the running time as linear as in practical situations. CS 473 Lecture X 2

Analysis Of Union By Rank With Path Compression We shall examine the function α to see just how it slowly grows. Then, rather than presenting the very complex proof of O(mα(m, n)) we shall offer a simpler proof of a slightly weaker upper bound O(mlg*n) on the running time. We will prove an O(mlg*n) bound on the running time of the disjoint set operations with union-by-rank & path-compression in order to prove this bound. In order to prove this bound: We first prove some simple properties of ranks. CS 473 Lecture X 3

Properties of Ranks LEMMA 1: For all nodes x (a) rank[x] ≤ rank[p[x]] If x ≠ p[x] then rank[x] ≤ rank[p[x]] (b) rank[x] is initially 0 Increases through time until x ≠ p[x], then, it does not change value (c) rank[p[x]] is a monotonically increasing function of time CS 473 Lecture X 4

Properties of Ranks Proof of (b) and (c) is trivial After a MAKE-SET(x) operation x is a root node & rank[x] = 0 • Rank of only root nodes may increase during a LINK operation • A non-root node may never become a root node Q. E. D Proof of (a) is by induction on the number of LINK & FIND-SET operations. CS 473 Lecture X 5

Inductive Proof Of Lemma 1 BASIS: True before the first LINK & FIND-SET operations since rank[x] = rank[p[x]] = 0 for all x’s INDUCTIVE STEP: Assume that the lemma holds before performing the operation LINK(x, y). • Let rank denote the rank just before the LINK operation. • Let rank' denote the rank just after the LINK operation. CS 473 Lecture X 6

Inductive Proof Of Lemma 1 CASE: rank[x] ≠ rank[y] • Assume without loss of generality that rank[x] < rank[y] • Node y becomes the root of the tree formed by the link • No rank change occurs rank'[x] = rank[x] rank'[y] = rank[y] • Only the parent of x changes from p[x] = x to p[x] = y but rank'[x] < rank'[y = p[x]] due to case assumption CS 473 Lecture X 7

Inductive Proof Of Lemma 1 CASE: rank[x] = rank[y] • Node y becomes the root of the new tree • Only the rank of node y changes as rank'[y] = rank[y] + 1 • Only the parent of x changes from p[x] = x to p[y] = y rank'[y] = rank[y] + 1 = rank[x] + 1 = rank'[x] + 1 so rank'[y = p[x]] > rank'[x] CS 473 Lecture X 8

Proving the Time Bound We will use the aggregate method of amortized analysis to prove the O(mlg*n) time bound. We will assume that we invoke the LINK operations rather than the UNION operation i. e. assume that appropriate FIND-SET operations are performed. The following lemma shows that, even if we count the extra FIND-SET operations the asymptotic running time remains unchanged. CS 473 Lecture X 9

Proving the Time Bound LEMMA: Suppose we convert a sequence S' of m' MAKE-SET, UNION and FIND-SET operations into a sequence S of m MAKE-SET, LINK and FIND-SET operations by turning each UNION into two FIND-SET operations followed by a LINK. If sequence S runs in O(mlg*n) time, then, sequence S' runs in O(m'lg*n) time. CS 473 Lecture X 10

Proving the Time Bound PROOF: We have m' ≤ m ≤ 3 m' since each union operation in S' is converted to 3 operations in sequence S. Since m = O(m') O(mlg*n) for the converted sequence S implies O(m'lg*n) for the original sequence S' of m' operations. CS 473 Lecture X 11

Proving the Time Bound THEOREM: A sequence of m MAKE-SET, LINK and FIND-SET operations, n of which are MAKE-SET operations, can be performed on a disjoint-set with union-by-rank and path-compression in worst case time O(mlg*n). PROOF: • We assess charges corresponding to the actual cost of each set operation then, compute the total number of charges assessed. • Once the entire sequence of operations has been performed, this total gives the actual cost of all the set operations. CS 473 Lecture X 12

Proving the Time Bound • The charges assessed to MAKE-SET and LINK operations are simpler one charge per operation. • Since these operations each take O(1) actual time, the charges assessed are equal to the actual costs. Before discussing charges assessed to the FIND-SET operations we partition node ranks into blocks by putting rank r into block lg*r for r = 0, 1, …, . Recall that CS 473 is the maximum rank. Lecture X 13

Proving the Time Bound The blocks are numbered as Bj for j = 0, 1, 2, …, jmax where jmax = lg*(lg n) = lg*n – 1 For notational convenience, we define for integers j ≥ -1 CS 473 Lecture X 14

Proving the Time Bound Then, for j = 0, 1, …, (lg*n – 1) the j-th block Bj consists of the set of ranks {B(j-1) + 1, B(j-1) + 2, …, B(j)} Note that two ranks r 1 & r 2 belong to the same block iff lg*r 1 = lg*r 2 Note that B(j) = 2 B(j-1) for j ≥ 0 CS 473 Lecture X 15

Proving the Time Bound Examples to the block concept Let n = 64 K = 216 = rmax = = = 16 ; r = {0, 1, 2, 3, …, 16} jmax = lg*n - 1 = lg - 1 = (3 + 1) - 1 = 3 ; j = {0, 1, 2, 3} B 0 = {B(-1)+1, …, B(0)} = { , …, 1} = {0, 1} B 1 = {B(0)+1, …, B(1)} = {1+1, …, 2} = {2} B 2 = {B(1)+1, …, B(2)} = {2+1, …, 22} = {3, 4} B 3 = {B(2)+1, …, B(3)} = {22+1, …, } = {5, …, 16} = {5, 6, 7, 8, …, 16} CS 473 Lecture X 16

Proving the Time Bound Examples to the block concept Let n = 264 K = rmax = = = 64 K = 216; r = {0, 1, 2, 3, …, 65536} jmax = lg*n - 1 = lg - 1 = (4 + 1) - 1 = 4 ; j = {0, 1, 2, 3, 4} B 0 = {0, 1} B 1 = {2} B 2 = {3, 4} B 3 = {5, 6, 7, 8, …, 16} B 4 = {17, 18, 19, 20, 21, …, 65536} CS 473 Lecture X 17

Proving the Time Bound We use two types of charges for a find-set operation: Block Charges and Path Charges Consider the FIND-SET(x 0) operation Assume that find path where xl is the root of the tree containing node x 0 p[xi] = xi+1 for i = 0, 1, 2, 3, …l-1 We assess one block charge to the last node with rank in block j on the find path to the child of the root, i. e. CS 473 Lecture X 18

Proving the Time Bound Because ranks strictly increase along any find path we effectively assess block charge to each node where p[xi] = xl (xi is the root or its child) lg*(rank[xi]) < lg*(rank[xi+1]) We assess one path charge to each node on the find path for which we do not assess a block charge. CS 473 Lecture X 19

Proving the Time Bound FACT: Once a node other than the root or its child is assessed block charges, it will never again be assessed path charges. PROOF: Each time path compression occurs, the rank of a node for xi which p[xi] ≠ xl remains the same but, a new parent of xi has a rank > rank of its old parent. The difference between the ranks of xi & its parent is a monotonically increasing function of time. CS 473 Lecture X 20

Proving the Time Bound Once xi & p[xi] have ranks in different blocks they will always have ranks in different blocks. So, xi will never again be assessed a path charge. Since we charge once for each node visited in each FIND-SET total number of charges assessed = total number of nodes visited in all FIND-SET operations. Thus, total number of charges represents actual cost of all FIND-SETs we wish to show that this total is O(mlg*n) CS 473 Lecture X 21

Proving the Time Bound on the number of block charges At most one block charge assessed for each block number on the FP plus one block charge for the child of the root. Since block numbers change from 0 to lg*n – 1 at most lg*n+1 block charges assessed for each FIND-SET Thus, at most m(lg*n + 1) block charges assessed over all FIND-SET operations. CS 473 Lecture X 22

Proving the Time Bound on the number of path charges If a node xi is assessed a path charge, then p[xi] ≠ xl so that xi will be assigned a new parent during path compression. Moreover, xi’s new parent has a higher rank than its old parent. Suppose that, node x’s rank is in block j. CS 473 Lecture X 23

Proving the Time Bound How many times can xi be assigned a new parent and thus assessed a path charge before xi is assigned a parent whose rank is in a different block after which xi will never again be assessed a path charge. This number of times is maximized if xi has the lowest rank in its block, namely B(j-1) + 1 and its parents’ rank successively on values B(j-1) + 2, B(j-1) + 3, …, B(j) We conclude that a vertex can be assessed at most B(j) – B(j – 1) – 1 path charges while its rank is in block j. CS 473 Lecture X 24

Proving the Time Bound on the number of path charges…continued Hence, we should bound the number of nodes N(j) whose ranks are in block j. By Lemma 4: For j = 0; CS 473 Lecture X 25

Proving the Time Bound For j ≥ 1; N(j) ≤ = = = Thus, CS 473 ≤ = = for all integers j ≥ 0. Lecture X 26

Proving the Time Bound on the number of path charges…continued We can bound the total number of path charges P(n) by summing over all blocks the product of • The maximum number of nodes with ranks in the block, and • The maximum number of path charges per node in that block CS 473 Lecture X 27

Proving the Time Bound P(n) ≤ = = Thus, the total number of charges incurred by FIND-SET operations is O(m(lg*n + 1) + nlg*n) = O(mlg*n) since m ≥ n Since there are O(n) MAKE-SET & LINK operations with one charge each, the total time is O(mlg*n). CS 473 Lecture X 28

Properties of Ranks Define size(x) to be the number of nodes in the tree rooted at x, including node x itself LEMMA 2: For all tree roots x size(x) 2 rank[x] PROOF: By induction on the number of LINK operations NOTE: FIND-SET operations change neither the rank not the size of a tree CS 473 Lecture X 29

Properties of Ranks BASIS: True for the first link since size(x)=1 & rank[x]=0 initially INDUCTION: Assume that lemma holds before performing LINK(x, y) Let: • rank & size denote the rank & size just before the LINK operation • rank' & size' denote the rank & size just after the LINK operation CS 473 Lecture X 30

Properties of Ranks CASE: rank[x] rank[y] rank'[x] rank[x] & rank'[y] rank[y] Assume without loss of generality that: rank[x] < rank[y] Node y becomes the root of the tree formed by the LINK operation CS 473 Lecture X 31

Properties of Ranks size'(y) case size(x) + size(y) 2 rank[x] + 2 rank[y] DUE TO INDUCTION 2 rank[y] 2 rank'[y] since rank'[y] rank[y] in this No ranks or size changes for any nodes other than y. CS 473 Lecture X 32

Properties of Ranks CASE: rank[x] rank[y] node y becomes the root of the new tree size'(y) CS 473 size(x) + size(y) 2 rank[x] + 2 rank[y]+1 2 rank'[y] Lecture X 33

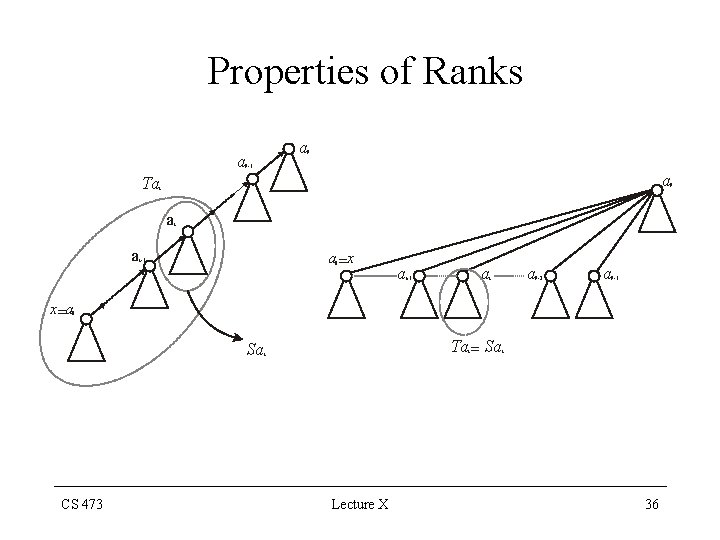
Properties of Ranks INDUCTIVE STEP: Assume that the lemma holds before performing the operation FIND-SET(x) Let rank denote the rank just before the FIND-SET operation and rank' denote the rank just after the FIND-SET operation Consider the find-path of node x: FPx {a 0=x, a 1, a 2, . . . , aq} CS 473 Lecture X 34

Properties of Ranks WHERE: ai for i 1, 2, . . . , q are the ancestors of node x a 0 a 1 p[a 0 x], a 2 p[a 1], . . . , ai p[ai-1] . . . aq p[aq-1] and aq is the root of the tree containing node x Only the parents of node x and in FPx change as p[x] aq and p[di] aq for i 1, 2, . . q-1 CS 473 Lecture X 35

Properties of Ranks a 9 -1 a Ta 9 i a a i a =x i-1 0 a a a i-1 9 -2 i a 9 -1 x =a 0 Ta = Sa Sa i i CS 473 Lecture X i 36

Properties of Ranks Due to induction; rank[a 0=x] < rank[a 1] < … < rank[aq-2] < rank[aq-1] < rank[aq] However, FIND-SET operation does not make any rank update. Therefore rank'[y] = rank[y] for any node rank'[x] < rank'[aq=p[x]] rank'[a 1] < rank'[aq=p[a 1]. . . rank'[aq-2] < rank'[aq=p[aq-2]] CS 473 Lecture X 37

Properties of Ranks Analysis of FIND-SET(x) operations…continued Let denote the tree rooted at ai just before the FIND-SET, and denote the tree rooted at ai just before the FIND-SET Tree rooted at nodes a 2, a 3, …, aq-1, aq change after FIND-SET, i. e. = for i = 2, 3, 4, …, q Hence, height of these nodes may change after FIND-SET. In fact, their height may decrease after a FIND-SET. CS 473 Lecture X 38

Properties of Ranks Since, FIND-SET operation does not update rank values; (old) rank values are still upper bounds on the heights of trees rooted at these nodes after FIND-SET. In fact, only the rank value of the root node aq is important since rank value only of this node may be checked during a future LINK operation. Hence, a tree with greater height may be linked to a tree with smaller height during a LINK operation. However, the important point is the following fact. CS 473 Lecture X 39

Properties of Ranks FACT: If size(aq) ≥ 2 rank[aq] before FIND-SET(x) operation then size'(aq) ≥ 2 rank'[aq] after FIND-SET(x) operation where aq is the root of tree containing node x PROOF: Trivial since FIND-SET operation does not change the size and the rank of the tree. CS 473 Lecture X 40

Properties of Ranks Consider the Following Sequence MAKE-SET(x 1). . . MAKE-SET(x 8) UNION(x 2, x 1) UNION(x 4, x 3) UNION(x 6, x 5) UNION(x 8, x 7) CS 473 rank=1 1 x x x 5 x 7 x 2 x 4 x 6 x 8 1 3 rank[x 1]=rank[x ]=1 2 Lecture X 41

Properties of Ranks Consider the Following Sequence x 1 UNION(x 3, x 1) UNION(x 7, x 5) rank[x 1]=rank[x 5]=2 x 3 x 7 x 4 CS 473 x 5 x 6 x 8 Lecture X 42

Properties of Ranks Consider the Following Sequence 1 UNION(x 8, x 4) 5 x 5 ← FIND-SET(x 8) x 1 ← FIND-SET(x 4) 4 3 2 8 7 6 1 LINK(x 5, x 1) 5 8 CS 473 7 4 3 2 6 Lecture X 43

Properties of Ranks Consider the last UNION operation UNION(x 8, x 4) size(x 1) = 4; rank(x 1) = 2; size(x 5) = 4; 23 = 8 rank(x 5) = 2; size'(x 1) = 8 height(x 1) = 2; height(x 5) = 2; height'(x 1) = 2 rank'(x 1) = 3 Hence, rank'[x 1] is a loose upper bound on the height of . However, rank'[x 1] is a tight lower bound on the log of size of . CS 473 44 Lecture X

Properties of Ranks LEMMA 3: For any integer r ≥ 0 there at most n/2 r nodes of rank r PROOF: Trivial for r = 0; there at most n/20 = n nodes of rank 0 • Fix a particular value of r > 0 • Suppose that when we assign a rank r to a node x we attach a label x to all nodes in the tree rooted at x • Lemma 2 assures that at least 2 r nodes are labeled each time since size(x) ≥ 2 r for a node x with rank r. • Note that, a new rank > 0 is assigned to a node CS 473 Lecture X 45

Properties of Ranks • Only we link two trees of equal rank during a UNION rank[x]=r-1 y rank[y]=r-1 rank[y]=r x Tx Ty size[y] ≥ 2 r-1 x y size[x] nodes are labeled with x size[x] = size[Tx] ≥ 2 r CS 473 Lecture X 46

Properties of Ranks Consider the nodes in Tx Whenever their roots change due to a LINK during a future UNION Lemma 1 ensures that the rank of the new root > r. • Thus, each node is labeled at most once when its root is first assigned the rank r. • Since there are n nodes there at most n labeled nodes with at least 2 r labels assigned for each node of rank r. • If there were more than n/2 r nodes of rank r then more than 2 r∙n/2 r = n nodes would be labeled. CONTRADICTION CS 473 Lecture X 47

Properties of Ranks COROLLARY: Every node has rank at most PROOF: If we let max. rank r > lg n due to Lemma 3, there at most n / 2 r nodes of rank r. However in this case n/2 r < n/2 lg n = 1 Hence, the number of nodes of rank r > lg n is < 1 Q. E. D. CS 473 Lecture X 48