CS 473 Algorithms I Lecture Network Flows Finding

CS 473 -Algorithms I Lecture ? Network Flows Finding Max Flow 1

FORD-FULKERSON METHOD / ALGORITHM • iterative algorithm: start with initial flow f =[0] with |f| = 0 – at each iteration, increase | f | by finding an augmenting path – repeat this process until no augmenting path can be found – by max-flow min-cut thm: upon termination this process yields a max flow FORD-FULKERSON-METHOD(G, s, t) initialize flow f to 0 while an augmenting path p do augment flow f along path p return f CS 473 Lecture ? 2

FORD-FULKERSON METHOD / ALGORITHM • basic Ford-Fulkerson Algorithm: data structures – note (u, v) Ef only if (u, v) E or (v, u) E – maintain an adj-list representation of directed graph G' = (V', E'), where • E' = {(u, v): (u, v) E or (v, u) E}, i. e. , – for each v Adj[u] in G' maintain the record v f(u, v) cf (u, v) – note: G' used to represent both G and Gf , i. e. , for any edge (u, v) E' • c[u, v] > 0 (u, v) E and cf [u, v] > 0 (u, v) Ef CS 473 Lecture ? 3

FORD-FULKERSON METHOD / ALGORITHM FORD-FULKERSON (G', s, t) for each edge (u, v) E' do f [u, v] ← 0 cf [u, v] ← 0 Gf ← COMPUTE-GF(G', f) while an s t path p in Gf do cf (p) ← min {cf [u, v]: (u, v) p} for each edge (u, v) p do f [u, v] ← f [u, v] + cf (p) CANCEL(G', u, v) Gf ← COMPUTE-GF(G', f) CS 473 COMPUTE-GF (G', f) for each edge (u, v) E' do if c[u, v] – f [u, v] > 0 then cf [u, v] ← c[u, v] – f[u, v] else cf [u, v] ← 0 return G' CANCEL (G', u, v) min ← {f [u, v], f [v, u]} f [u, v] ← f [u, v] – min f [v, u] ← f [v, u] – min Lecture ? 4

FORD-FULKERSON ALGORITHM • augmenting path in Gf is chosen arbitrarily • performance if capacities are integers: O(E |f*|) – while-loop: time to find s t path in Gf = O(E') = O(E) – # of while-loop iterations: ≤ |f*|, where f* = max flow • so, running time is good if capacities are integers and |f*| is small CS 473 Lecture ? 5

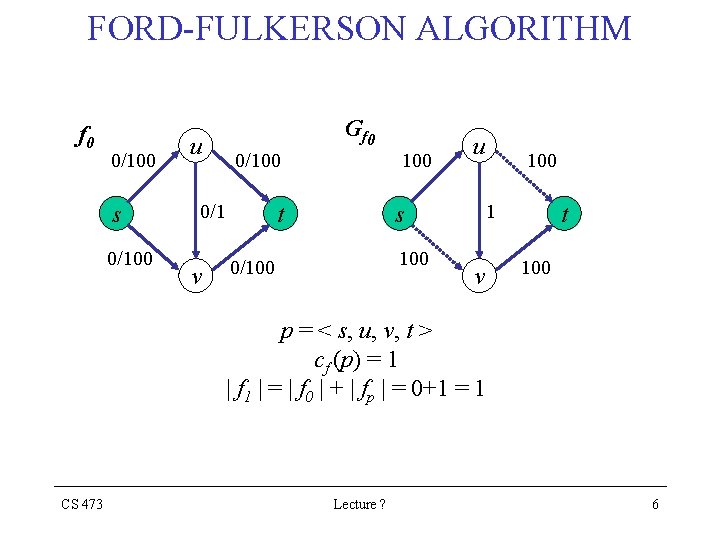
FORD-FULKERSON ALGORITHM f 0 0/100 s 0/100 u G f 0 0/100 0/1 v 100 t u 1 s 100 0/100 v t 100 p = < s, u, v, t > cf (p) = 1 | f 1 | = | f 0 | + | fp | = 0+1 = 1 CS 473 Lecture ? 6

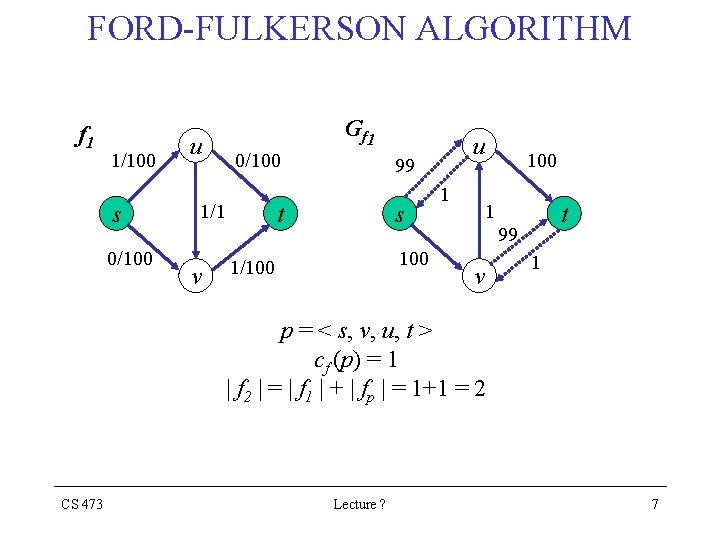
FORD-FULKERSON ALGORITHM f 1 1/100 s 0/100 u G f 1 0/100 1/1 v u 99 t s 100 1/100 1 t 99 v 1 p = < s, v, u, t > cf (p) = 1 | f 2 | = | f 1 | + | fp | = 1+1 = 2 CS 473 Lecture ? 7

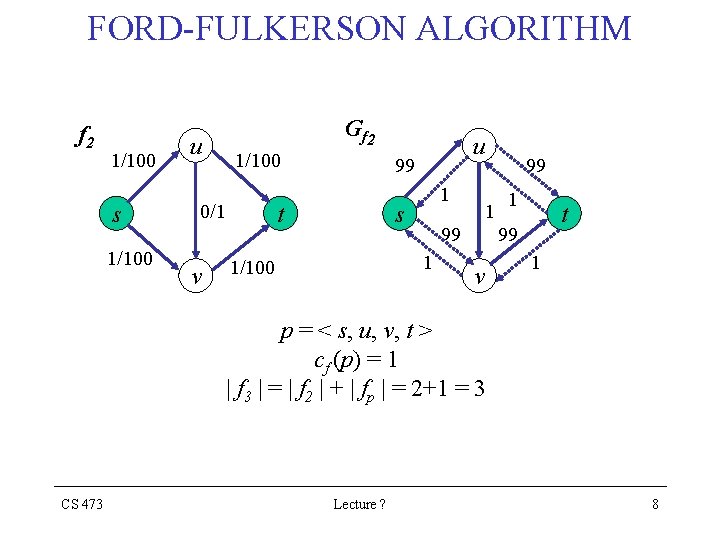
FORD-FULKERSON ALGORITHM f 2 1/100 s 1/100 u G f 2 1/100 0/1 v u 99 t 1 s 1 99 1 1/100 99 1 t 99 v 1 p = < s, u, v, t > cf (p) = 1 | f 3 | = | f 2 | + | fp | = 2+1 = 3 CS 473 Lecture ? 8

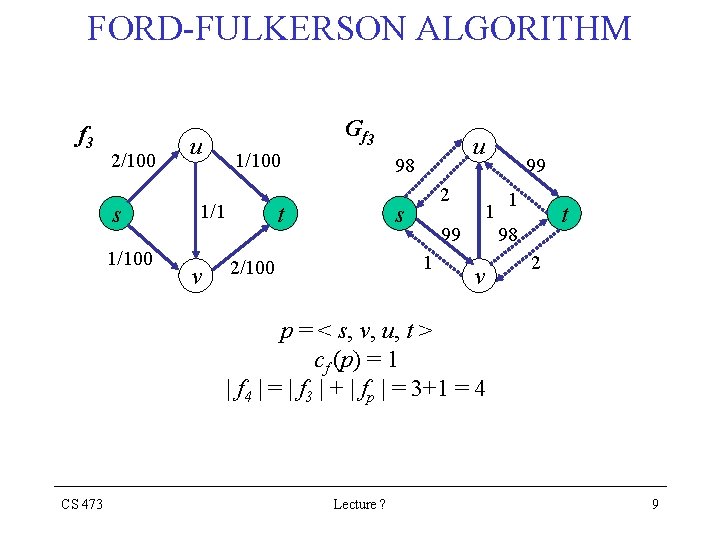
FORD-FULKERSON ALGORITHM f 3 2/100 s 1/100 u G f 3 1/100 1/1 v u 98 t 2 s 1 99 1 2/100 99 1 t 98 v 2 p = < s, v, u, t > cf (p) = 1 | f 4 | = | f 3 | + | fp | = 3+1 = 4 CS 473 Lecture ? 9

FORD-FULKERSON ALGORITHM • choose p = < s, u, v, t > in odd iterations • choose p = < s, v, u, t > in even iterations – 200 augmentations to reach |f*| = 200 • might never terminate for non-integer capacities • efficient algorithms: – augment along max-capacity path in Gf: not mentioned in textbook – augment along breadth-first path in Gf: Edmonds-Karp algorithm O(VE 2) CS 473 Lecture ? 10

EDMONDS-KARP ALGORITHM • def: δf (s, v) = shortest path distance from s to v in Gf – unit edge weights in Gf δf (s, v) = breadth-first distance from s to v in Gf • L 7: v V – {s, t}; δ (s, v) in Gf’s increases monotonically with each augmentation • proof: suppose – (i) a flow f on G induces Gf – (ii) fp along an augmenting path in Gf produces f’ = f + fp on G – (iii) f’ on G induces Gf’ • notation: δ(s, v) = δf (s, v) and δ’(s, v) = δf’ (s, v) CS 473 Lecture ? 11

ANALYSIS OF EDMONDS-KARP ALGORITHM • want to prove: δ' (s, v) ≥ δ(s, v) v V – {s, t} • for contradiction: assume δ'(s, v) < δ(s, v) for some v • without loss of generality: assume δ' (s, v) is minimal over all such vertices – i. e. , δ' (s, v) < δ' (s, u) u V – {s, t} δ' (s, u) < δ(s, u) – thus δ' (s, u) < δ' (s, v) δ' (s, u) ≥ δ(s, u) (1) CS 473 Lecture ? 12

ANALYSIS OF EDMONDS-KARP ALGORITHM • consider a shortest s v path p': s u → v in Gf’ Øδ'(s, u) = δ'(s, v) – 1 by “subpath is also a shortest path” δ' (s, u) < δ' (s, v) by (1), δ' (s, u) ≥ δ(s, u) (2) Øconsider this edge (u, v) Ef ': question: was (u, v) Ef ? ØYES: i. e. , (u, v) Ef ' and (u, v) Ef ; note f(u, v) < c(u, v) • δ(s, v) ≤ δ(s, u) + 1 by triangle inequality ≤ δ' (s, u) + 1 by (2) = δ' (s, v) ≥ δ(s, v) contradiction CS 473 Lecture ? 13

ANALYSIS OF EDMONDS-KARP ALGORITHM • NO: i. e. , (u, v) Ef ' but (u, v) Ef ; note f(u, v)=c(u, v) – fp pushes flow back along edge (u, v) (v, u) p in Gf – i. e. , augmenting path p is of the form p = s v → u t – note: p is a breadth-first path from s to t (Edmond-Karp algorithm) – δ(s, v) = δ(s, u) – 1 by “subpath is also a shortest path” ≤ δ' (s, u) – 1 by (2) = (δ' (s, v) – 1 by “subpath is also a shortest path” = δ' (s, v) – 2 < δ'(s, v)Lecture ≥ δ(s, v) contradiction 14 CS 473 ?

ANALYSIS OF EDMONDS-KARP ALGORITHM • what is the bound on the total # of augmentations? • def: an edge (u, v) in Gf is critical on an augmenting path p in Gf if cf (u, v) = cf (p) • at least one edge on an augmenting path must be critical • a critical edge disappears from Gf after the augmentation – f '(u, v) = (f+fp)(u, v) = f (u, v) + fp(u, v) = f (u, v) + (c(u, v) – f (u, v)) = c(u, v) cf ' (u, v) = c'(u, v) – f '(u, v) = c(u, v) – c(u, v) = 0 CS 473 Lecture ? 15

ANALYSIS OF EDMONDS-KARP ALGORITHM • Thm: number of flow augmentations is O(EV) • proof: find a bound on the number of times an edge (u, v) becomes critical – let (u, v) becomes critical the first time along path = s u → v t in Gf p • δ(s, v) = δ(s, u) + 1 (1), since p is a shortest path – then (u, v) disappears from the residual network – (u, v) can reappear an another augmenting path • only after net flow from u to v is decreased – this only happens if (v, u) appears on an augmenting path CS 473 Lecture ? 16

ANALYSIS OF EDMONDS-KARP ALGORITHM • assume this event occurs along a path p' = s u → v t in Gf ' later – δ'(s, u) = δ'(s, v) + 1 since p' = s u → v ≥ δ(s, v) + 1 by L 7 = (δ(s, u) + 1 since p' = s u → v = δ(s, u) + 2 δ' (s, u) ≥ δ(s, u) + 2 t is a shortest path • i. e. , δ(s, u) increase by ≥ 2 each time (u, v) becomes critical, except the first time • thus each edge (u, v) can become critical at most O(V) times, since – 1 ≤ δ(s, u) ≤ | V | - 2 and δ(s, u) never decreases by L 7 • (E) edges in Gf’s # of flow augmentations = O(VE) • running time of Edmonds-Karp algorithm: |E|× O(VE) = O(E 2 V) – finding an augmenting path in a Gf = breadth-first search = O(E) CS 473 Lecture ? 17

MAXIMUM BIPARTITE MATCHING PROBLEM • many combinatorial optimization problems can be reduced to a max-flow problem • maximum bipartite matching problem is a typical example CS 473 Lecture ? 18

MAXIMUM BIPARTITE MATCHING PROBLEM • given an undirected graph G = (V, E) • def: a matching is a subset of edges M E such that v V, at most one edge of M is incident to v • def: a vertex v V is matched by a matching M if some edge M is incident to v, otherwise v is unmatched • def: a maximum matching M* is a matching M of maximum cardinality, i. e. , |M*| ≥ |M| for any matching M • def: G=(V, E) is a bipartite graph if V=L R where L∩R= such that E={(u, v): u L and v R} CS 473 Lecture ? 19

MAXIMUM BIPARTITE MATCHING PROBLEM • applications: job task assignment problem – Assigning a set L of tasks to a set R of machines – (u, v) E task u L can be performed on a machine v R – a max matching provides work for as many machines as possible CS 473 Lecture ? 20

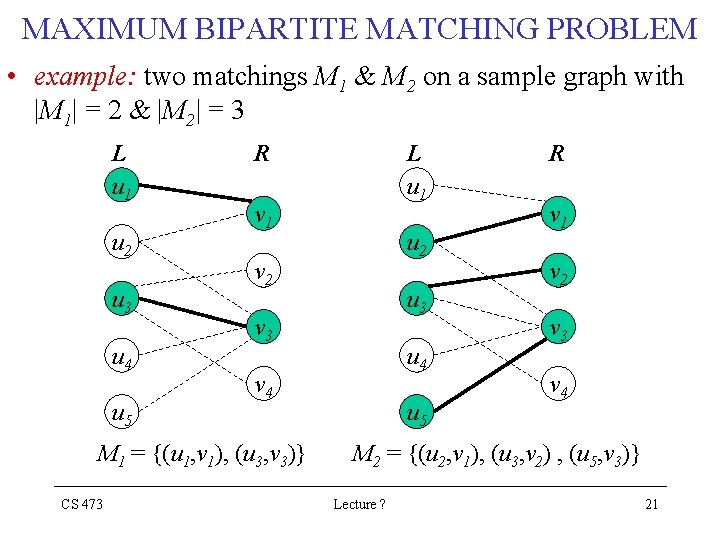
MAXIMUM BIPARTITE MATCHING PROBLEM • example: two matchings M 1 & M 2 on a sample graph with |M 1| = 2 & |M 2| = 3 L u 1 u 2 u 3 u 4 u 5 R v 1 u 2 v 2 u 3 v 3 u 4 v 4 M 1 = {(u 1, v 1), (u 3, v 3)} CS 473 L u 1 u 5 R v 1 v 2 v 3 v 4 M 2 = {(u 2, v 1), (u 3, v 2) , (u 5, v 3)} Lecture ? 21

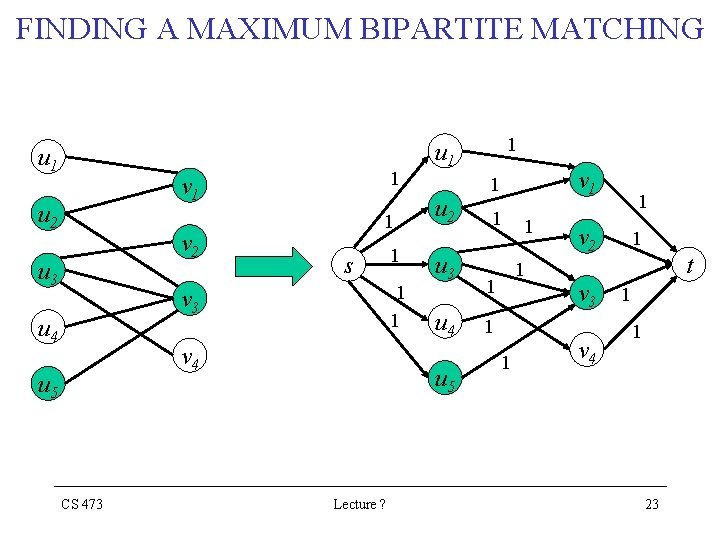
FINDING A MAXIMUM BIPARTITE MATCHING • idea: construct a flow network in which flows correspond to matchings • define the corresponding flow network G'=(V', E') for the bipartite graph as – V' = V {s} {t} s, t V – E' = {(s, u): u L} {(u, v): u L, v R, (u, v) E} {(v, t): v R} – assign unit capacity to each edge of E' CS 473 Lecture ? 22

FINDING A MAXIMUM BIPARTITE MATCHING u 1 1 v 1 u 2 v 2 u 3 1 s 1 1 v 3 u 4 v 4 u 5 CS 473 1 v 1 1 u 2 u 3 u 4 u 5 Lecture ? 1 u 1 1 1 1 v 2 v 3 v 4 1 t 1 1 23

FINDING A MAXIMUM BIPARTITE MATCHING • def: a flow f on a flow network is integer-valued if f(u, v) is integer u, v V • L 8: (a) IF M is a matching in G, THEN an integer-valued f on G' with | f | = |M| (b) IF f is an integer-valued f on G', THEN a matching M in G with | M | = | f | CS 473 Lecture ? 24

FINDING A MAXIMUM BIPARTITE MATCHING • proof L 8 (a): let M be a matching in G – define the corresponding flow f on G' as • u, v M; f(s, u)=f(u, v)=f(v, t) = 1 & f(u, v) = 0 for all other edges • first show that f is a flow on G': – 1 unit of flow passes thru the path s → u → v → t for each u, v M • these paths are disjoint s t paths, i. e. , no common intermediate vertices – f is a flow on G' satisfying capacity constraint, skew symmetry & flow conservation • because f can be obtained by flow augmentation along these s t disjoint paths CS 473 Lecture ? 25

FINDING A MAXIMUM BIPARTITE MATCHING • second show that | f | = |M|: – net flow accross the cut ({s} L, R {t}) = | f | by L 3 – | f | = f (s L, R t) = f (s, R t) + f (L, R) + f (L, t) = 0 + f (L, R) + 0; f (s, R t) = f (L, t) since no such edges = f (L, R) = |M| since f(u, v) = 1 u L, v R & (u, v) M CS 473 Lecture ? 26

FINDING A MAXIMUM BIPARTITE MATCHING • proof L 8 (b): let f be a integer-valued flow in G' – define M={(u, v): u L, v R, and f (u, v) > 0} • first show that M is a matching in G: i. e. , all edges in M are vertex disjoint – let pe(u) / pl(u) = positive net flow entering / leaving vertex u, u V – each u L has exactly one incoming edge (s, u) with c(s, u)=1 pe(u) ≤ 1 u L CS 473 Lecture ? 27

FINDING A MAXIMUM BIPARTITE MATCHING – since f is integer-valued; u L, pe(u) = 1 pl(u) = 1 due to flow conservation u L, pe(u)=1 exactly one vertex v R f(u, v) = 1 to make pl(u) = 1 – thus, at most one edge leaving each vertex u L carries positive flow = 1 – a symmetric argument holds for each vertex v R – therefore, M is a matching CS 473 Lecture ? 28

FINDING A MAXIMUM BIPARTITE MATCHING • second show that |M| = | f |: – |M| = f (L, R) by above def for M since f (u, v) is either 0 or 1 = f (L, V' – s – L – t) f (L, V') = 0 = f (L, V') – f (L, s) – f (L, L) – f (L, t) due to flow cons. f (L, t) = 0 since no = 0 – f (L, s) – 0 edges from L to t = – f (L, s) = f (s, L) = | f | due to skew symmetry & then def. CS 473 Lecture ? 29

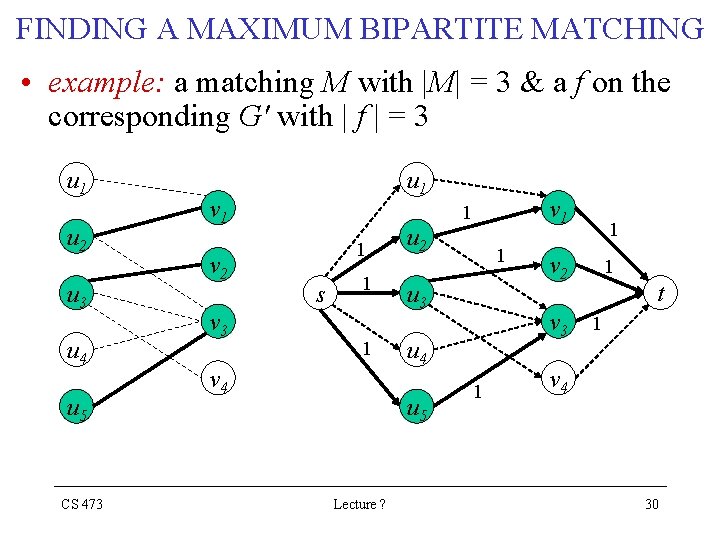
FINDING A MAXIMUM BIPARTITE MATCHING • example: a matching M with |M| = 3 & a f on the corresponding G' with | f | = 3 u 1 u 2 u 3 u 4 u 5 CS 473 u 1 v 2 v 3 v 1 1 1 s 1 1 v 4 u 2 u 3 v 2 v 3 u 4 u 5 Lecture ? 1 1 t 1 v 4 30