Complexity Theory Lecture 7 Lecturer Moni Naor Recap

Complexity Theory Lecture 7 Lecturer: Moni Naor

Recap Last week: • Non-Uniform Complexity Classes • Polynomial Time Hierarchy – – BPP in hierarchy If NP µ P/Poly the hierarchy collapses – Approxiamte Counting in the hierarchy This Week: – – Randomized Reductions #P Completeness of Permanent

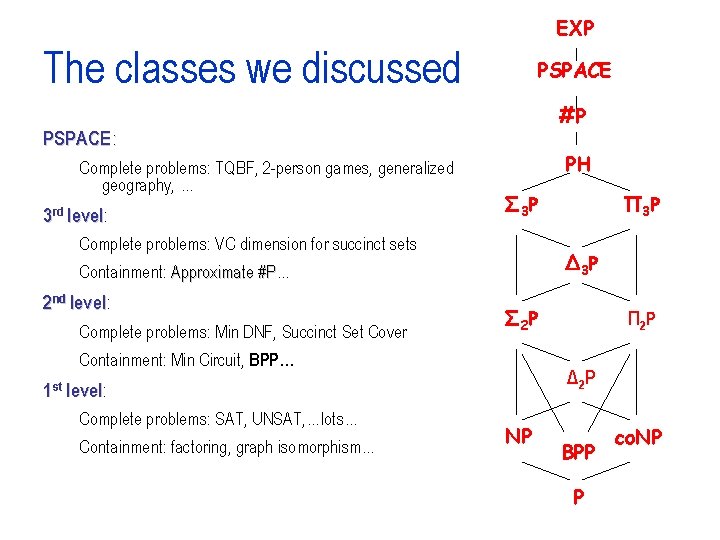
EXP The classes we discussed PSPACE #P PSPACE : Complete problems: TQBF, 2 -person games, generalized geography, … 3 rd level: level PH Σ 3 P Complete problems: VC dimension for succinct sets Δ 3 P Containment: Approximate #P… #P 2 nd level: level Complete problems: Min DNF, Succinct Set Cover Σ 2 P Containment: Min Circuit, BPP… Containment: factoring, graph isomorphism… Π 2 P Δ 2 P 1 st level: level Complete problems: SAT, UNSAT, …lots… Π 3 P NP BPP P co. NP

Approximate Counting is in the Hierarchy Theorem: For any f 2 #P there is a g 2 Δ 3 P such that on input x and g(x, ) outputs a (1+ ) approximation to f(x) (1 - )g(x, ) · f(x) · (1+ )g(x, ) Proof: key point – method for proving that sets are certain size The set in question: A = Accept(M(x)) µ {0, 1}m A function f is in #P if there exists a NTM M running in polynomial oftime where M(x) has f(x) accepting paths for all x 2 {0, 1}n

Methods for proving sizes of sets Let H be family of hash functions where for h 2 H h: {0, 1}m {0, 1}ℓ • if h 2 H is 1 -1 on A then clearly |A| · 2ℓ – a bit difficult to expect full uniqueness • Relaxed property: No collisions property if there are h 1, h 2, … hℓ 2 H are such that – for all x 2 A there is an 1 · i · l where for all x’ 2 A{x} we have hi(x) hi(x’) then we know |A| < ℓ 2ℓ Claim: for a pair-wise independent family H, if |A|· 2ℓ-1 , then there exist h 1, h 2, … hℓ 2 H with the no collisions property. Denote with UH(A, ℓ). Claim: for A=Accept(M) we have UH(A, ℓ) 2 Σ 2 P Can eliminate the quantifier on i by explicitly going over all possibilities! Conclusion: with oracles calls to UH(A, ℓ) can find smallest ℓ for which UH(A, ℓ) holds Yields a 2ℓ approximation for f(x) • Can use amplification of f(x) by running M k times (from accepting positions). New machine M will have fk(x) by accepting paths

Pair-wise Independent Hash Functions A family of hash functions H={h|h: {0, 1}m {0, 1}ℓ } is pair-wise independentif: for all x ≠ y, for random h 2 RH the random variables h(x), h(y) are uniformly distributed and independent In particular: Pr[h(x)=h(y)]= 1/2ℓ Already saw the approximate version for distributed equality testing Pr[h(x)=h(y)]· Constructing H: • Construction based on matrix multiplication. – Treat x as a m £ 1 vector. – The function is defined by a random m£ ℓ matrix over GF[2]. H={h. A|A 2 GF[2]m£ ℓ and h. A(x)=Ax } Nice property: local computation

Proof of No Collisions Claim • For any x 2 A and any x’ 2 A{x} if h is chosen at random from H Prh[h(x)=h(x’)]= 1/2ℓ • By the Union bound Prh[h(x) is unique] ¸ |A| ¢ 1/2ℓ ¸ 1/2 • Hitting set: Construct h 1, h 2, … hℓ one by one, each time covering at least ½ of elements in A that have not been unique so far – Let A’ be the set not covered so far – For any x 2 A’ and any x’ 2 A{x} for random h 2 R H Prh[h(x) is unique] ¸ |A| ¢ 1/2ℓ ¸ ½. Note: this is the full A

Checking No Collisions Claims Given h 1, h 2, … hℓ and A (in the form of Accept(M)) how to check the no collisions claim: • First observation: 8 x 2 A 9 i 2 {1, …, ℓ} 8 x’ 2 A{x}: hi(x) hi(x’) this is in 3 P • Quantification over i‘s is limited: can change order and replace with explicit enumeration 8 x, x 1, x 2, …, xℓ 2 A if x {x 1, x 2, …, xℓ} then h 1(x) h 1(x 1)Ç h 2(x) h 2(x 2) Ç …Ç hℓ(x) hℓ(xℓ) this is in 1 P=Co. NP

Second Proof of No Collisions Claim • For any x 2 A and any x’ 2 A{x} if h is chosen at random from H Prh[h(x)=h(x’)]= 1/2ℓ • By the Union bound Prh[h(x) is unique] ¸ |A| ¢ 1/2ℓ ¸ ½. • Choose h 1, h 2, … hℓ at once. – For every x 2 A for each i Pr[hi(x) is unique] ¸ ½. – Probability that at least one i is unique for x is at least 1 -1/2ℓ – With probability at least ½ choice is good for all x 2 A. Conclusions: – There is a choice that is good for all x 2 A. – Approximate Counting is in BPP NP – Choose h 1, h 2, … hℓ and check the no collisions claim

Approximate Counting and Uniform Generation • For self reducible problems: – Exact counting implies exact uniform generation of witnesses/solutions Choose to set x 1=1 with probability proportional to # (1, x 2, …xn)/# (x 1, x 2, …xn) – Approximate counting: almost uniform generation of solutions • Accumulated error is multiplicative (1+p(n)) Theorem: if P=NP then given Boolean circuit C possible to sample almost uniformly at random satisfying assignment to C Reverse is also true: from uniform sampling to approximate counting

From Uniform Generation to Approximate Counting • Reverse is also true: from uniform sampling to approximate counting • For #SAT we know # (x 1, x 2, …xn) = # (1, x 2, …xn) + # (0, x 2, …xn) • To get an approximation: generate n 2/ 2 assignments • Learn the ration # (1, x 2, …xn) and # (0, x 2, …xn) Conclusion: Uniform Generation to Approximate Counting are the same for self reducible problems Spun a whole industry of Markov Chain/Monte Carlo algorithms Notable successes: • Approximating the volume of a convex body • Approximating the permanent

More on BPP in the Hierarchy Simultaneous Provers • To prove BPP ½ S 2 P we considered a game between and players – player wants to prove x L and player wants to prove x L • In S 2 P setting first makes a move and then player (based on ’s move) What if both players have to move simultaneously? • Want strategy where – player wins whenever x L even if player makes move after player Homework: • Phrase the above requirements in terms of a polynomial time relation R(x, y, z) • Show that for all L BPP such a strategy exists

Homework problem discussion: low memory device A low memory device is given a stream of a 1, a 2 … an and then b 1, b 2 … bn where ai, bi 2 {0, 1}ℓ and has to determine whether the two multisets are equal. whethere is a a permutation of the a' s that gives the b's • Solution: fix a finite field F (larger than 2ℓ) and choose Degree n random z 2 F poly in z • Compute (as you go) i=1 n (z-ai) and i=1 n (z-bi) – if the two values are not equal – then two streams are not equal – if the two values are equal – then two streams are equal –except with probability at most n/|F| Can get slightly better probability using -bias probability spaces

Application: low memory verification of satisfiability Suppose that there is a 3 -CNF and a low memory device wishes to verify that it is satisfiable. • Device has access to : can verify whether the jth clause of is a given one Prover: To convince the device that a given assignment satisfies : • 1. 2. Verifier: Send first in order of clauses for each clause (x 1 Ç x 2Ç x 3) the value of the assignment on x 1, x 2, x 3 Send in order of variables for each variable xi : (number of times appears in , value of the assignment on xi ) verify that clauses are correct and assignment satisfies each clause. Problem: how to check consistency between occurrences of xi translate into two streams of ai and bi – each occurrence of xi in first part to ai =(i, xi ) – each occurrence in second part to bi =(i, xi ) (repeat for number of occurrences in ) • Check equality of streams

Problems with unique solutions • An instance of SAT may have many satisfying assignments • Does the hardness of SAT stem from the multiple assignments – Maybe it is harder to walk towards the right solution if there are several of them • Promise problem: we are told that the number of satisfying assignments is 0 or 1. Can we determine which is the case? – Not responsible if more than a single assignment

Randomized reduction to unique solutions Valiant-Vazirani Theorem: there is a randomized poly-time procedure that given a 3 CNF formula (x 1, x 2, …, xn) outputs a 3 -CNF formula ’ such that: – if is not satisfiable, then ’ is not satisfiable – if is satisfiable, then with probability at least 1/(8 n): ’ has exactly one satisfying assignment Idea of procedure: project the assignments via hashing and look for the event “only one satisfying assignment hashed to 0 k” k should be log number of satisfying assumptions want to express it uniquely

Expressing uniqueness • Want to use hashing via matrix multiplication – Need to express the statement (x 1, x 2, …, xn) (y 1, y 2, …, yn)=0 over GF[2] with a unique satisfying assignment Claim: for each Y=(y 1, y 2, …, yn) there exists a 3 -CNF formula θY on x 1, x 2, …, xn and additional variables such that: – | θY | = O(n) – θY is satisfiable iff an even number of variables in {xi yi}i=1 n are 1 – for each setting of the xi variables, this satisfying assignment is unique Proof: scan from left to right computing the inner product so far Introduce z 0, z 1, …, zn and add clause(s) for i=1, …, n – (zi = zi-1 ) if yi=0 – (zi = zi-1 © xi ) if yi=1 and (z 0 =1) and (zn =1) Not surprising: can do for any function in P using circuit simulation

The Reduction Procedure: – Choose random k 2 R {0, 1, 2, …, n-1} – for i = 1, 2, …, k • pick random subset Yi 2 R {0, 1}^n – output ’ = k = θY θY 1 2 Let T be the set of satisfying assignments for Claim: if |T| > 0, then Prk {0, 1, 2, …, n-1}[2 k-2 ≤ |T| ≤ 2 k-1] ≥ 1/n Good guess k

Unique Solutions Denote (Y 1 X, Y 2 X, YKX) with h(X) Claim: if 2 k-2 ≤ |T| ≤ 2 k-1(good guess), then the probability k has exactly one satisfying assignment is at least 1/8 • Fix X T. Let event Ax be “h(X)=0 and for all X’ T{X}: h(X’) ≠ 0” – Pr[h(X)= 0] = (½)k. – For all X’ T{X}: Pr[h(X’) = 0| h(X) = 0] = (½)k – Pr[8 X’ T{X} h(X’) ≠ 0| h(X)] ¸ 1 -|T|/2 k ¸ ½. – Pr[Ak] ¸ (½)k+1 At most 2 k-1 • Since events Ax are disjoint from each other Pr[ k has exactly one satisfying assignment] ¸ |T| (½)k+1 ¸ 1/8 At least 2 k-2

No RP Algorithms for Unique SAT unless… • Since the good guess event is independent of the choice of Y 1, Y 2, …, Yk we get the probability of success is at least 1/(8 n). Corollary: if there is an RP algorithm for deciding Unique SAT, then NP=RP Proof: If there is a an algorithm for deciding Unique SAT then there one for finding the satisfiable assignment if it is unique Self reducibility Run the reduction several times and then run the unique sat finding algorithm Can make no errors if not satisfiable

Alternative Proof Isolation Lemma • Let (X, S) be a set system – Each s 2 S is a subset of ground set X – |X|=m • Let w: X {1, …, 2 m} be a positive weight function chosen uniformly and independently at random in {1, …, 2 m} • Then Pr[set with minimum weight is unique in S] ¸ ½.

Proof of Isolation Lemma For each element i 2 X and weights for all elements in X{i} w 1, w 2, …, wi-1, wi+1 …, wm can consider critical value t 2 Z for w(i): t may be negative or larger than 2 m • If w(i) < t, then minimum weight set must contain i • If w(i) > t, then minimum weight set does not contain i Pr[w(i)=t] · 1/2 m Claim: If no i 2 X is at critical value (w. r. t. other weight), then minimum is unique Proof: If two different sets s 1 and s 2 are the minimum weight sets then there is and i 2 s 1 and i s 2 (or vice versa). Pr[some w(i) is at critical value] · m ¢ 1/2 m · ½.

Applications of the Isolation Lemma Minimum weight matching: given a graph G=(V, E) with m edges assign random weights to edges from {1, …, 2 m}. • With probability at least ½ the minimum weight perfect matching is unique – Let X=E and S={U ½ E| U is a perfect matching} and apply the Isolation Lemma Homework: use the Isolation Lemma to show another reduction to unique sat You may find it most useful to consider the max clique problem

Reductions between functions • Reduction from function problem A to function problem B – two efficiently computable functions Reduction and Reconstruction. In functions, reducing one problem A to another B involves 1. A mapping of the instances x of A to instances y of B 2. A reconstruction process: answering A(x) from the answer to B(y) x Reduction A A(x) y B Reconstruction B(y)

Reductions and #P • • A function f is in #P if there exists a NTM M running in polynomial time where M(x) has f(x) accepting paths for all x 2 {0, 1}n problem f is #P-complete if – – f is in #P every problem in #P is in FPf par·si·mo·ni·ous adj. Excessively sparing or frugal. Parsimonious Reductions: • For counting problems we call a reduction parsimoniousif the reconstruction is the identity - preserves the number of solutions – – many standard NP-completeness reductions are parsimonious therefore: if #SAT is #P-complete we get lots of #P-complete problems More expressive term: witness preserving reductions

#SAT: given a 3 -CNF how many satisfying assignments to are there? Theorem: #SAT is #P-complete. Proof: – clearly in #P: ( , x) R x satisfies – take any f #P defined by relation R P • Essentially Cook-Levin Reduction, but let’s look inside

#P-Completeness of #SAT …x… f(x) =|{y : (x, y) R}| …y… C 1 iff (x, y) R Circuit for R – Add new variables z, produce #-CNF such that z (x, y, z) = 1 C(x, y) = 1 – For (x, y) such that C(x, y) = 1 this z is unique • Can express for each gate using 3 -CNF thatzi is the correct computation – hardwire x – # satisfying assignments = |{y : (x, y) R}| Homework: show that #Clique is #P-Complete

Relationship to other classes • To compare to classes of decision problems, usually consider P#P Easy connections: • NP, co. NP P#P • P#P PSPACE Toda’s Theorem: PH P#P. So approximate #P PH P#P Big surprise: counting can express iterating quantifiers

Counting vs. Deciding Question: are problem #P complete because they require finding NP witnesses? – or is the counting difficult by itself? Already saw one counter-example: #DNF But not really convincing given tight connection to CNF

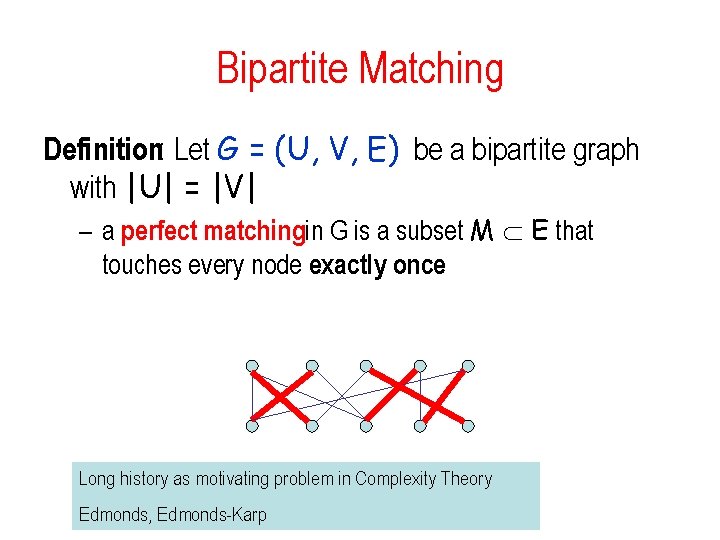
Bipartite Matching Definition: Let G = (U, V, E) be a bipartite graph with |U| = |V| – a perfect matchingin G is a subset M E that touches every node exactly once Long history as motivating problem in Complexity Theory Edmonds, Edmonds-Karp

Bipartite Matchings #MATCHING: given a bipartite graph G = (U, V, E) how many perfect matchings does it have? Theorem (Valiant): #MATCHING is #P-complete. • But: can find a perfect matching in polynomial time! • No seemingly related problem that is NP-Complete – counting itself must be difficult The fact that computing #MATCHING is NP-Hard is surprising in itself. The #P completeness is an extra bonus

The Permanent • The permanent of a matrix A is defined as: per(A) = ΣπΠi. Ai, π(i) Compare to the determinant of a matrix A det(A) = Σπ sgn(π) Πi. Ai, π(i) • # of perfect matchings in a bipartite graph G is exactly the permanent of G’s adjacency matrix AG – a perfect matching defines a permutation that contributes 1 to the sum

The Permanent • Valiant’s Theorem says that the permanent of {0, 1} matrices is #Pcomplete – permanent has many nice properties that make it a favorite of complexity theory Contrast permanent (hard) per(A) = ΣπΠi. Ai, π(i) to determinant (easy): det(A) = Σπ sgn(π) Πi. Ai, π(i) As a result computing per(A) mod 2 is easy Important difference between the two: – det(A B) = det(A) det(B) for all matrices – but per(A B) ≠ per(A) per(B) in general Homework: show

Cycle Covers • Bipartite graph G = (U, V, E) – Adjacency square matrix AG – Corresponding directed graph with self loops • Cycle cover in a directed graph: collection of node disjoint cycles that covers all the nodes • One-to-one correspondence between matchings and cycle covers Can think of representation of permutation in two ways – Explicit enumeration – Cycle decomposition Number of perfect matching = Number of cycle covers in corresponding graph • Weighted graph – the permanent of general matrices – Sum over all cycle covers – For each cycle cover take the product of the weights – Negative weights can zero out positive ones If this gadget appears as a subgraph – zeroes out the whole cycle cover Green edge: weight -1 Black edge: weight 1 Cycle cover 0

Proof Structure • Show the hardness of the permanent problem for general integer matrices – Build a series of gadgets (weighted graphs) – For a given a 3 CNF formula with n variables and m clauses • map each satisfying assignment into cycle covers of weight 4 m of weight • non-satisfying assignments yield cycle covers whose total contribution is 0 • Reduce the computation to {0, 1} matrices

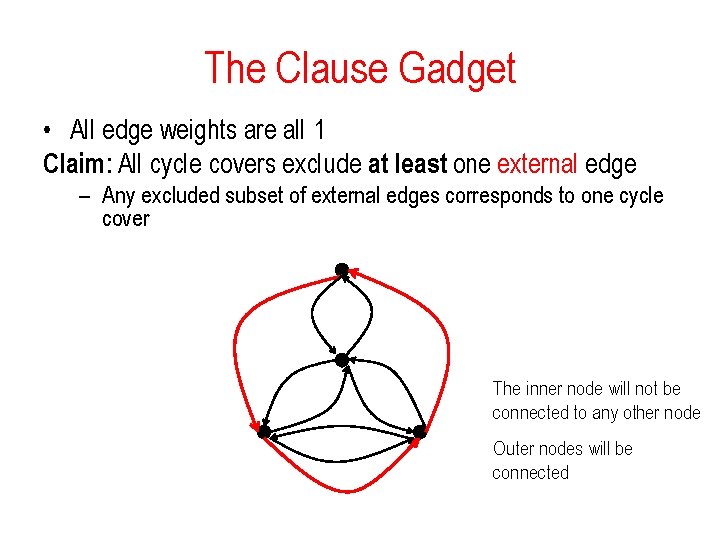
The Clause Gadget • All edge weights are all 1 Claim: All cycle covers exclude at least one external edge – Any excluded subset of external edges corresponds to one cycle cover The inner node will not be connected to any other node Outer nodes will be connected

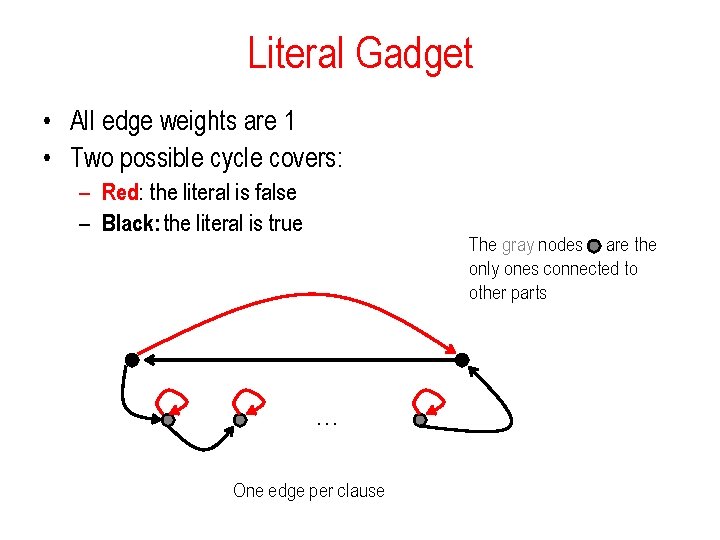
Literal Gadget • All edge weights are 1 • Two possible cycle covers: – Red: the literal is false – Black: the literal is true The gray nodes are the only ones connected to other parts … One edge per clause

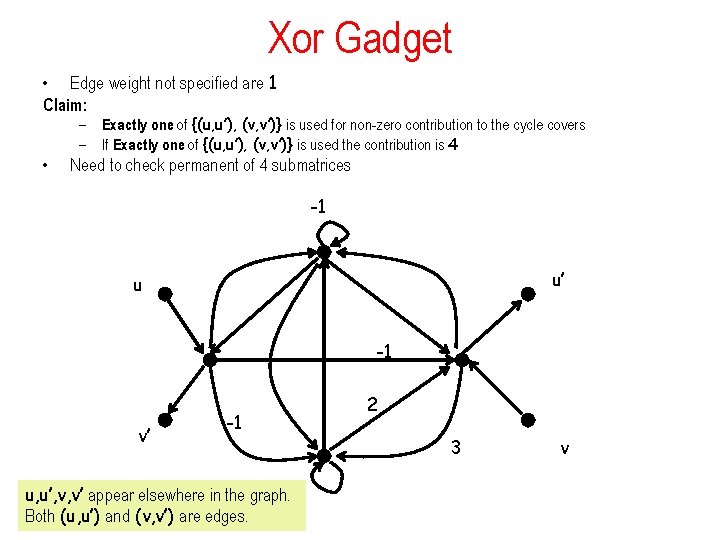
Xor Gadget • Edge weight not specified are 1 Claim: • – Exactly one of {(u, u’), (v, v’)} is used for non-zero contribution to the cycle covers – If Exactly one of {(u, u’), (v, v’)} is used the contribution is 4 Need to check permanent of 4 submatrices -1 u’ u -1 v’ -1 u, u’, v, v’ appear elsewhere in the graph. Both (u, u’) and (v, v’) are edges. 2 3 v

Embedding the Gadgets • For each clause make a clause gadget – Identify each external edge with a literal • Connect each external edge with its literal via an Xor gadget • Connect the two literals of variable via an Xor gadget Claim: total weight of cycle covers is s 4 m where s is the number of satisfying assignments Any assignment that does comply with the restrictions adds zero

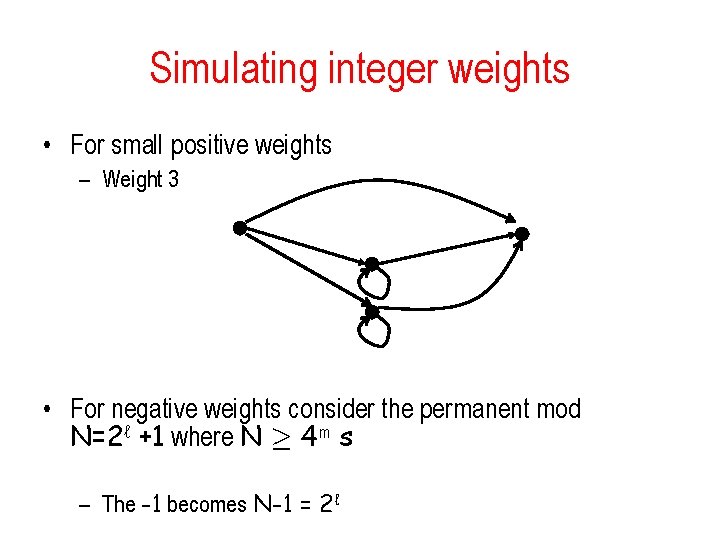
Simulating integer weights • For small positive weights – Weight 3 • For negative weights consider the permanent mod N=2ℓ +1 where N ¸ 4 m s – The -1 becomes N-1 = 2ℓ

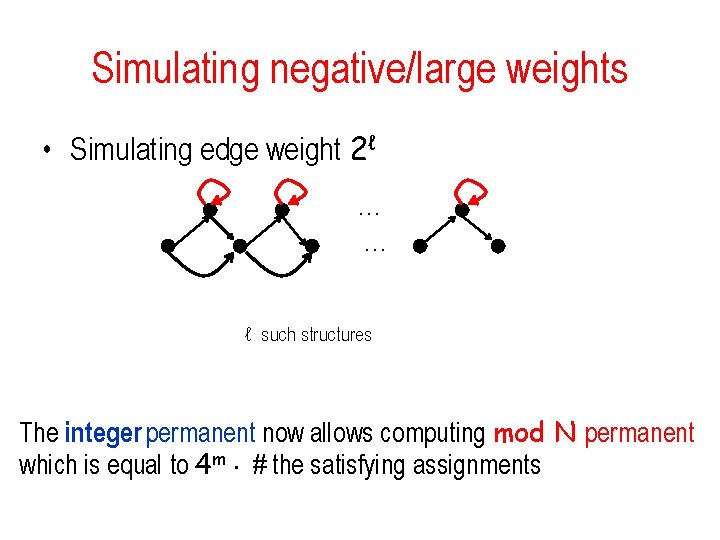
Simulating negative/large weights • Simulating edge weight 2ℓ … … ℓ such structures The integer permanent now allows computing mod N permanent which is equal to 4 m ¢ # the satisfying assignments

References • Unique Sat: Leslie Valiant and Vijay Vazirani, 1985 • Isolation Lemma: Ketan Mulmuley, Umesh Vazirani and Vijay Vazirani – Motivation: parallel randomized algorithm for matching based on matrix inversion. • Checking with low memory devices: – Blum and Kannan, Lipton • #P-Completeness of the Permanent: Valiant, 1979.