Complexity Theory Lecture 4 Lecturer Moni Naor Recap

Complexity Theory Lecture 4 Lecturer: Moni Naor

Recap Last week: Space Complexity • Savitch’s Theorem: NSPACE(f(n)) µ SPACE(f 2(n)) – Collapse of NPSPACE to PSPACE • PSPACE Completeness – TQBF, Games • Logarithmic space – deterministic and non • Sublogarithmic space • Non-deterministic space is closed under complementation This week: Probabilistic Space Complexity

The Central Questions of Complexity Theory Log. Space µ NL µ P µ NP µ PSPACE Are any of the containments proper? All we can say: NL ( PSPACE Since NL µ Space(log 2 n) ( PSPACE from diagonalization (space hierarchy) Is NP = Co-NP? Is P = NP Å Co-NP ? Have not seen yet power of: • Oracles • Interaction • Randomization If P = NP Å Co-NP then factoring is easy

2 -SAT: given a formula = C 1 Æ C 2 … Æ Cm where Ci =( Ç ) where 2 {xj, : xj} and 2 {xk, : xk} for some j and k. Is there a satisfying assumption for ? Let G( ) be a directed graph with – Nodes: literals – Edge ( , ) iff clause (: Ç ) exists Represent the implication the constraint puts Claim: is satisfiable iff for no xi are there both a path from xi to : xi and a path from : xi to xi in G( ) Corollary: 2 -SAT is in NL easy to see 2 -unsat in NL and apply Immerman--Szelepcsenyi

2 -SAT is Complete for NL • Reduce from (un)reachability of DAGs – This is NL-Complete as well • Given a DAG G, source s and target t construct (G): Log space construction – For each node x create variable x – For edge (x, y) 2 G: add clause (: x Ç y) – Add clauses (s) and (: t) Claim: (G) is satisfiable iff there is no path from s to t in G

Algorithm for 2 -SAT • Start with arbitrary assignment • While the assignment is not satisfying – Choose an arbitrary unsatisfied clause Ci =( Ç ) – Choose at random from { , } and flip the assignment to that variable – If unsuccessful for many step stop and declare `unsat’ Analysis: let A 2 {0, 1}n be any satisfying assignment – With probability at least ½ distance to A is reduced – With probability at most ½ distance to A is increased 0 n

Analysis of Algorithm Distance can never be larger than n Want to compute how long it takes a pebble to get with high probability to 0 Dominated: for all t probability exact if it starts at some 0 · i · n process takes more than t steps is at least as the original process Dominated by a walk where – With probability exactly ½ distance to A is reduced – With probability exactly ½ distance to A is increased – When pebble hits 0 it is absorbed – When pebble hits n it is reflected 0 n

Analysis of Random Walks Would like to be able to say: Expected time to visit 0 For what time period can we say that there high probability?

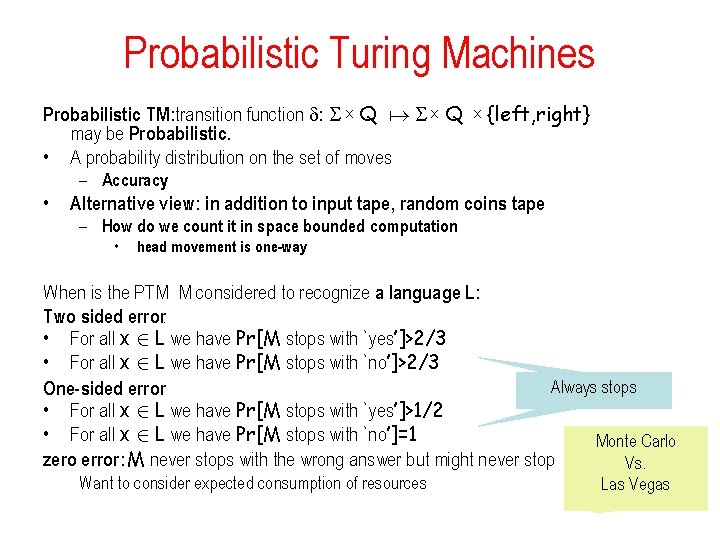
Probabilistic Turing Machines Probabilistic TM: transition function : X Q may be Probabilistic. • A probability distribution on the set of moves X {left, right} – Accuracy • Alternative view: in addition to input tape, random coins tape – How do we count it in space bounded computation • head movement is one-way When is the PTM M considered to recognize a language L: Two sided error: • For all x 2 L we have Pr[M stops with `yes’]>2/3 • For all x 2 L we have Pr[M stops with `no’]>2/3 Always stops One-sided error • For all x 2 L we have Pr[M stops with `yes’]>1/2 • For all x 2 L we have Pr[M stops with `no’]=1 Monte Carlo zero error: M never stops with the wrong answer but might never stop Vs. Want to consider expected consumption of resources Las Vegas

Random Log. Space (RL) • A probabilistic Turing Machine with worktape size O(log |X|) – Long enough to count and assure stopping in time RL: one-sided Error • For all x 2 L we have Pr[M stops with `yes’]>1/2 • For all x 2 L we have Pr[M stops with `no’]=1 BPL: two-sided Error • For all x 2 L we have Pr[M stops with `yes’]>2/3 • For all x 2 L we have Pr[M stops with `no’]>2/3 ZPL: No Error but stopping time is only expected polynomial time Show: ZPL= RL Å Co-RL

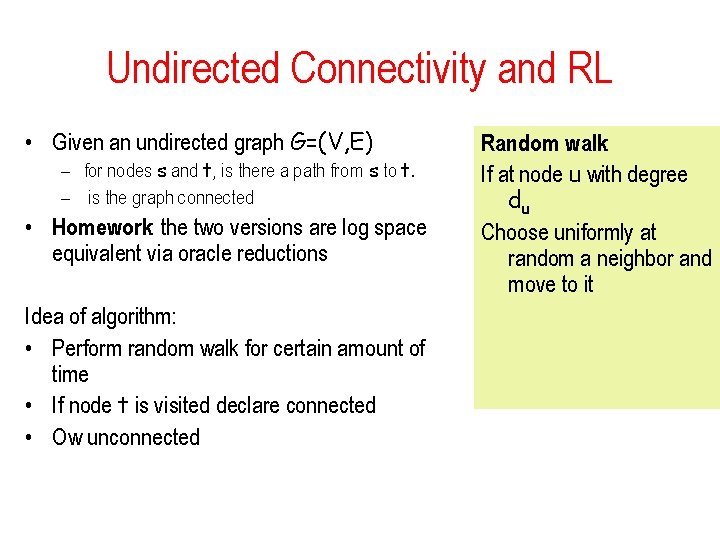
Undirected Connectivity and RL • Given an undirected graph G=(V, E) – for nodes s and t, is there a path from s to t. – is the graph connected • Homework: the two versions are log space equivalent via oracle reductions Idea of algorithm: • Perform random walk for certain amount of time • If node t is visited declare connected • Ow unconnected Random walk: If at node u with degree du Choose uniformly at random a neighbor and move to it

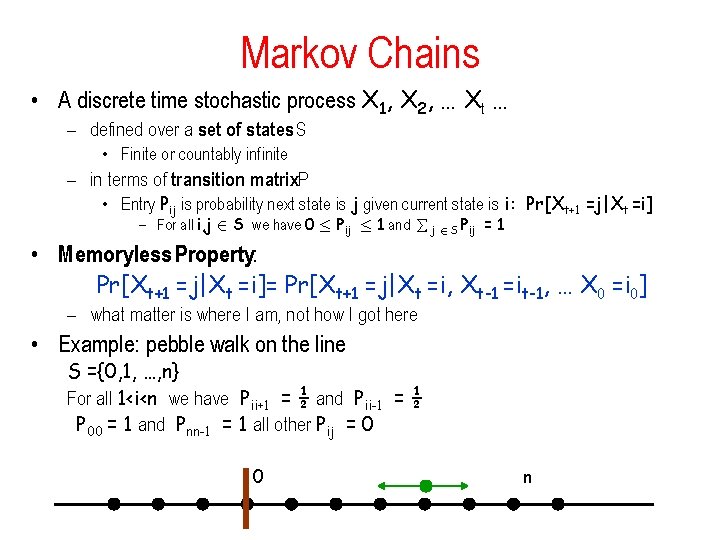
Markov Chains • A discrete time stochastic process X 1, X 2, … Xt … – defined over a set of states S • Finite or countably infinite – in terms of transition matrix. P • Entry Pij is probability next state is j given current state is i: Pr[Xt+1 =j|Xt =i] – For all i, j 2 S we have 0 · Pij · 1 and j 2 S Pij = 1 • Memoryless Property: Pr[Xt+1 =j|Xt =i]= Pr[Xt+1 =j|Xt =i, Xt-1 =it-1, … X 0 =i 0] – what matter is where I am, not how I got here • Example: pebble walk on the line S ={0, 1, …, n} For all 1<i<n we have Pii+1 = ½ and Pii-1 = ½ P 00 = 1 and Pnn-1 = 1 all other Pij = 0 0 n

Markov Chains • Initial state distribution q(0)=(q 1(0), q 2(0), … qn(0)) • State probability vector q(t)=(q 1(t), q 2(t), … qn(t)) distribution of the chain at time t q(t+1)=q(t)P and q(t)= q(0)Pt • Stationary distribution: for Markov Chain with transition matrix P is distribution such that = P If a Markov Chain is in a/the stationary distribution at step t it remains so forever Steady state behavior There can be unique, several or no stationary distribution Depending on the initial distribution

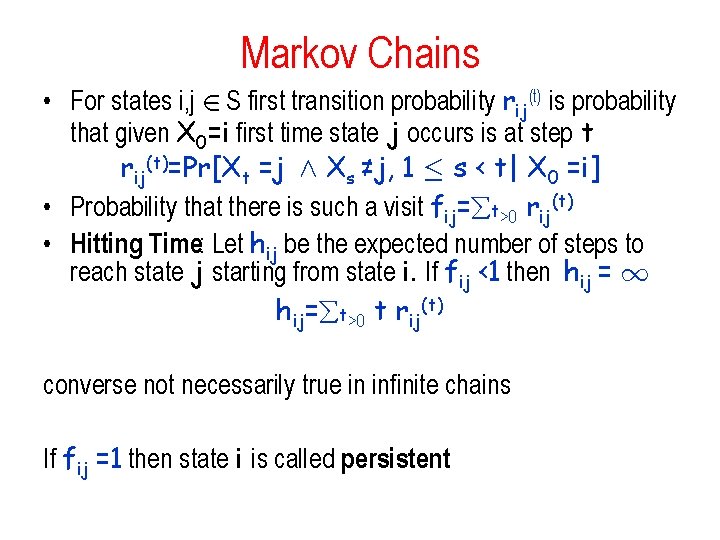
Markov Chains • For states i, j 2 S first transition probability rij(t) is probability that given X 0=i first time state j occurs is at step t rij(t)=Pr[Xt =j Æ Xs ≠j, 1 · s < t| X 0 =i] • Probability that there is such a visit fij= t>0 rij(t) • Hitting Time: Let hij be the expected number of steps to reach state j starting from state i. If fij <1 then hij = 1 hij= t>0 t rij(t) converse not necessarily true in infinite chains If fij =1 then state i is called persistent

Markov Chains • Underlying directed graph of a Markov Chain: Edge (i, j) iff Pij > 0 • Markov Chain is irreducible if its underlying graph consists of a single strong connected component • Periodicity of a state i: GCD of the lengths of the path from i back to itself – Bipartite graphs: periodicity 2 – State is aperiodic if it has period 1

Fundamental Theorem of Markov chains For any irreducible, finite and aperiodic Markov Chain: • All states are ergodic (hii < 1) • There is a unique Stationary distribution • For all i 2 S we have – i > 0 – fij = 1 – hii = 1/ i

Famous Markov Chain: Page. Rank algorithm [Brin and Page 98] • Good authorities should be pointed by good authorities • Random walk on the web graph – pick a page at random – with probability α follow a random outgoing link – with probability 1 - α jump to a random page • Rank according to the stationary distribution

Random Walks on Graphs Undirected graph G=(V, E), |E|=m, |V|=n • The transition matrix Puv = 1/du if (u, v) 2 E and 0 ow. Claim: is G=(V, E) is connected and non-bipartite then for all v 2 V v =du/2 m Conclusion: huu = 2 m/du How to make the graph non-bipartite? Add self-loops

Cover and Commute time • Commute time Cuv: expected time for a random walk starting at u to reach v and come back Cuv = huv+hvu • Cover time Cu(G): expected length of a walk starting at u, visiting every node at least once. C(G) =maxu Cu(G). Lemma: for any edge (u, v): Cuv = huv+hvu · 2 m Consider Markov chain of (directed) edges. Stationary distribution: uniform (each edge+direction) 1/2 m Time to get from u to v and back on edge (v, u): 2 m Not true for non-edges

Upper bound on Cover Time • Theorem: Cu(G)· 2 m (n-1) Proof: consider any spanning tree T of G. There is a traversal of T v 0, v 1, … v 2 n-2 where each edge of T is traversed once in each direction. Consider random walk starting and ending at v 0, that traverses each of the edge of T once in each direction Upper bound on walk is upper bound on cover time Cu(G)· j=02 n-3 hvj v j+1 = (u, w) 2 T Cuw · (n-1) 2 m At most m, from Lemma Conclusion: taking 4 n 3 as the bound in the random walk suffices for constant probability of success

Universal Traversal Sequences G is a regular graph of degree d • Labeling: the edges neighboring a node are labeled with {1, 2 …d} in an arbitrary manner – Port number • Can we find a polynomial sized sequence of labels s 1, s 2, … sk , si 2 {1, 2 …d} such that following it assures visiting all nodes of the graph Yes, it exists. Use the probabilistic method. • Fix a graph an labeling • Compute probability that sequence is not good for graph • Sum over all graphs (n. O(dn)) A log space construction puts connectivity in log space 4 7

Hot off the press news • Omer Reingold, Undirected ST-Connectivity in Log. Space, Available: Electronic Colloquium on Computational Complexity, Report TR 04 -094 Important Web Resources on Complexity: • ECCC: http: //www. eccc. uni-trier. de • Lance Fortnow’s Computational Complexity Web Log: http: //fortnow. com/lance/complog/

What happens in directed graphs • There are strongly connected directed graphs with an exponential covering time • Can count to doubly exponential space probabilistically • So if we do not insist on always stopping may do directed connectivity in random log space (but exponential time) – uninteresting

Probabilistic Variants of P RP: one-sided Error • For all x 2 L we have Pr[M stops with `yes’]>1/2 • For all x 2 L we have Pr[M stops with `no’]=1 BPP: two-sided Error • For all x 2 L we have Pr[M stops with `yes’]>2/3 • For all x 2 L we have Pr[M stops with `no’]>2/3 ZPP: No Error but stopping time is only expected polynomial time

The Schwartz-Zippel Algorithm/Theorem: Let Q(x 1, x 2, …, xn) 2 F(x 1, x 2, …, xn) be a non-zero muitivariate polynomial of total degree d. Fix any finite set S µ F and choose r 1, r 2, …, rn 2 R S. Then Pr[Q(r 1, r 2, …, rn)=0] · d/|S| Proof: by induction on n Useful when Q is not given explicitly and want to test equality to 0 Determinant of a matrix

Matching in Bipartite Graphs • Let G=(V, U, E) be a bipartite graph, |V|=|U|=n Define A to be the n £ n matrix with |E| variables Aij= xij if (i, j) 2 E and 0 otherwise Theorem (Edmonds): G has a perfect matching iff det(A)≠ 0 Proof: det(A)= 2 S sgn( ) A 1, (1) A 1, (2)… A 1, (n) n

Algorithm for deciding whether a matching exists in bipartite graphs • • Fix a prime P larger than 2 n Choose {rij}(i, j) 2 E 2 R GF[P] Compute det(A({rij}(i, j))) If non-zero declare matching. Ow, no matching • In general computing det(A) more expensive than running combinatorial algorithm for matching • Not true in parallel computation