Complexity Theory Lecture 6 Lecturer Moni Naor Recap

Complexity Theory Lecture 6 Lecturer: Moni Naor

Recap Last week: • Probabilistic Complexity 1. Schwatz-Zippel 2. Approximating Counting Problems Plus • Alternation This Week: • Non-Uniform Complexity Classes • Polynomial Time Hierarchy

Machines that Take Advice • Turing Machine with advice: extra read only tape – Advice string • Machine M decides language L with advice A(n) if: – X 2 L implies M(x, A(|x|) = `yes’ – X L implies M(x, A(|x|) = `no’ Advice A(n) is specific to the length Complexity Class with advice: C is a complexity class and f: N N. Language L 2 C/f(n) if there is a TM M and advice A(n) that decides language L and |A(n)| · f(n) Example: P/Poly(n) = [k P/n. K

P/Poly • Every unary language is in P/poly – There are undecidable languages in P/poly {1 index(x) | x L} where L is undecidable Observation: a language is in P/poly iff it has a polynomial sized circuit – There exists a sequence of circuits C 1, C 2, … and a polynomial p(n) such that: • circuit Cn computes f on inputs of size n • circuit Cn is of size at most p(n) What is the power of P/poly is NP 2 P/poly? Homework: show that if NP 2 P/log then P=NP

Circuits Let B be a collection of Booleans functions A Circuit for on n Boolean variables x 1, x 2, … xn over Basis B is a DAG with • • – Each source is labeled with a literal – Unique sink – Each internal node is labeled with a function from B and has the appropriate indegree A circuit compute a function in the natural way Which (families of) functions have circuits whose size is bounded by polynomial in the input size? – B ={: , Ç, Æ} Claim: all f 2 P have polynomial size circuits Proof: via the `usual’ tableau. Size of circuit T(n)S(n). Using Oblivious Turing Machines T(n) log T(n) Can determine the inputs to a given gate by a log space machine Claim: most Boolean function f on n variables do not have polynomial sized circuits For any polynomial p(n) most functions need more p(n) gates Need (2 n/n) gates to compute all functions on n variables, which is tight

Polynomial Sized Circuits for BPP • Theorem: any f 2 BPP has a polynomial size circuit – There exists a sequence of circuits C 1, C 2, … and a polynomial p(n) such that: • circuit Cn computes f on inputs of size n • circuit Cn is of size at most p(n) Several proofs (various derandomization methods): • Construction of hitting set (for f 2 RP) – Claim that a sequence r 1, r 2, … rn exists where for each x 2 L at least one ri says `yes’ • Simulating large sample spaces by small ones • Amplification – Reduce the error so that a single assignment will be good for all x

Derandomization I Collection that should resemble probability of success on ALL inputs Bad Good 1 - Chernoff Theorem: any f 2 BPP has a polynomial size circuit Simulating large sample spaces • Want to find a small collection of strings on which the PTM behaves as on the large collection – If the PTM errs with probability at most , then should err on at most + of the small collection • Choose m random strings • For input x event Ax is more than ( + ) of the m strings fail the PTM 2 m -2 Pr[Ax] · e < 2 -2 n Pr[[x Ax] · x Pr[Ax] < 2 n 2 -2 n=1

Derandomization A major research question: • How to make the construction of – Small Sample space `resembling’ large one – Hitting sets Efficient. Successful approach: randomness from hardness – (Cryptographic) pseudo-random generators – Complexity oriented pseudo-random generators

Alternation • Non-determinism: a configuration leads to acceptance if there is an accepting leaf in the computation – Similar to Or • Can also consider leads to acceptance if all leaves are accepting – Similar to And • What if we alternate between the modes

Alternating Turing Machines An Alternating Turing Machines(ATM) is a non-deterministic TM whose state S ={SAND [ SOR} are partitioned into two sets • For input x consider the tree of computations where each node is a configuration • The ATM is accepting if the root leads to an accepting configuration: – A leaf is accepting or not – A node in state s 2 SAND leads to acceptance if both its children leads to acceptance – A node in state s 2 SOR leads to acceptance if one of its children leads to acceptance

Alternating Time Classes ATIME(f(n))= class of language decided by an ATM where: • All computations halt after at most f(|x|) steps ASPACE(f(n))= class of language decided by an ATM where: • All computation halt • Never use more than f(|x|) cells AL = ASPACE(log n) Theorem: AL = P Theorem: by simulating circuit Important point: if f 2 P then the circuit is constructable in log space • Simulate the circuit from the output towards the inputs

Oracle Machines Recall: Oracle Turing Machine (OTM) have a special query tape where can ask membership queries and obtain answers • Oracle for A – can ask whether x 2 A • Oracle Machine with oracle for A: MA Can consider time classes with oracle CA • PA ={L|there is an OTM MA that decides L in polynomial time} • NPA ={L|there is an OTM MA that decides L in non deterministic polynomial time} Homework • Is PSAT = NPSAT ? Is PPSPACE = NPPSPACE ? Can consider Time Classes with oracle from another time class • PNP ={L|there is an OTM M AND a language A 2 L where MA decides L in polynomial time}

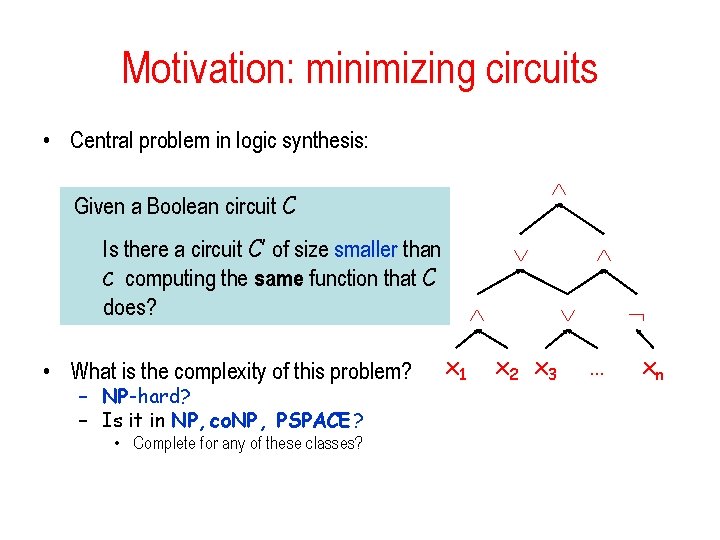
Motivation: minimizing circuits • Central problem in logic synthesis: Given a Boolean circuit C Is there a circuit C’ of size smaller than C computing the same function that C does? • What is the complexity of this problem? – NP-hard? – Is it in NP, co. NP, PSPACE? • Complete for any of these classes? x 1 x 2 x 3 … xn

The Polynomial-Time Hierarchy • Can define many complexity classes using oracles • Concentrate on classes that – have natural complete problems – have a natural interpretation in terms of alternating quantifiers – help state consequences and containments

The Polynomial Time Hierarchy Version I: Oracles • 0 P =P i. P • i+1 P = NP • i. P i+1 P = co. NP • PH = [i ¸ 0 i. P Notation sometimes i. P

Polynomial time hierarchy First level of the hierarchy: • • • 0 P 1 P = P =P 0 P 1 P = NP 0 P 1 P = Co. NP • If we believe the first level classes to be different from each other (and from the zero-level class(es)), are other levels also different? • Does equality at one level imply one at the other levels? • Are there interesting problems higher than the first level?

Polynomial time hierarchy Proposition: i. P i+1 P Proof: i. P i+1 P=P i. P Example NP co. NP PNP= 2 P We have an oracle for L i. P Ask the oracle and return answer for i. P Ask the oracle and return the opposite for i. P (which is co- i. P).

Polynomially Balanced Relations A binary relation R µ {0, 1}n £ {0, 1}n is polynomially balanced if – (x, y) 2 R, then |y|· |x|k for some k Characterization of NP in terms of witnesses: Claim: L 2 NP iff there is a polynomially balanced relation such that – R 2 P – L={x| 9 y such that (x, y) 2 R} Claim: L 2 Co. NP iff there is a polynomially balanced relation R 2 P such that L={x| 8 y such that |y| · |x|k, (x, y) 2 R}

The Polynomial Time Hierarchy Version II: Quantifiers Theorem: Let L be a language and i ¸ 1. L 2 i. P iff there is a polynomially balanced relation R such that – R 2 i-1 P and – L={x| 9 y such that (x, y) 2 R} Proof: by induction on i Interesting direction: show to build a certificate checkable in i-1 P from computation of NP machine with i-1 P oracle

Proof of Equivalence • Proof of Theorem: – induction on i – Have seen base case Oracle definition implies quantifier definition: Σ i-1 P • By definition Σ i. P = NPPi-1 P • Given L={x| 9 y such that (x, y)2 R} and R 2 i-1 P to see why it is in Σ i. P: Guess y, ask oracle if (x, y) R Can do since Σ i. P = NPPi-1 P

Proof of Equivalence Quantifier definition implies oracle definition: Given L Σi = NPΣi-1 decided by an Oracle NTM M running in time nk • First try: R = {(x, y) | y describes a valid path of M’s computation} – Valid path = leading to qaccept Problem: how to recognize valid computation path when it depends on results of oracle queries?

Proof of Equivalence R = { (x, y) | y describes valid path of M’s computation} Try – valid path = step-by-step description including correct yes/no answer for each A-oracle query zj (A Σi-1 P) e. g: z 1 A, z 2 2 A, z 3 A, … zm A – verify “no” queries in Pi-1 P: e. g: z 1 A z 3 A … zm A – for each “yes” query zj , by induction. 9 wj, |wj| ≤ |zj|k with (zj, wj) R’ for some R’ Pi-2 P For each “yes” query zj put wj in description of path y

Proof of Equivalence Single relation R in Pi-1 P : (x, y) R IFF – all “no” zj A and – all “yes” zj have (zj, wj) R’ and – y is a path leading to qaccept. Key Point: the AND of Pi-1 predicates is in Pi-1.

The Polynomial Time Hierarchy Version II Corollary: Let L be a language and i ¸ 1. L 2 i. P iff there is a polynomially balanced relation R such that – {(x, y)|(x, y) 2 R} 2 i-1 P and – L={x| 8 y with |y| · |x|k we have (x, y) 2 R} Proof: recall that i P is Co i. P Corollary: Let L be a language and i ¸ 1. L 2 i. P iff there is a polynomially balanced and polynomiallydecidable (i+1)-ary relation R such that – L={x| 9 y 1 8 y 2 9 y 3 …Q yi such that (x, y 1, y 2, … yi) 2 R} Quantifier Q is 9 if i is odd and Q is 8 if i is even Complete problem for i. P

Collapse of the Hierarchy Theorem: If for some i ¸ 1 i. P= i. P, then for all j ¸ i j. P= j. P Proof: suffices to show i. P= i. P implies i. P= i+1 P Corollary : If NP=Co. NP then the polynomial hierarchy collapses to the first level Similarly if P=NP

Interesting Languages in the hierarchy Minimum equivalent problems Minimum circuit: given a circuit C is it true that there is no circuit C’ with fewer gates that computes the same function as C Claim: Minimum circuit is in 2 P: 8 C’, |C’| < |C| 9 x such that C(x) C’(x) Minimum circuit is not known to be lower in the hierarchy or complete for 2 P

Complete Problems for 2 P Minimum DNF: given DNF , integer k; is there a DNF ‘ of size at most k computing same function does? – Example: x 1 x 2 x 3 x 1 x 3 x 4 x 1 x 2 x 1 x 3 x 4 Theorem: (Umans 98): Minimum DNF is Σ 2 P-complete

Complete Problems for 2 P Odd TSP: given a weighted graph G, is the length of the shortest TSP tour in G odd? Theorem: Odd TSP is Δ 2 P-complete Homework: Show Odd TSP is in Δ 2 P

Oracles vs. Algorithms • Given a polynomial time algorithm for SAT – Can you solve Minimum Circuit efficiently? – What other consequences? • Given an oracle for SAT same input/output behavior as algorithm! – Can you solve Minimum Circuit efficiently? Key issue: is access to a program as a black box give you more power then given the code itself Recent developments in cryptography show a difference (Barak 2001)

BPP in the Hierarchy • Do not know whether BPP µ NP – Do not know whether BPP≠EXP Theorem: BPP µ 2 P • Sufficient to show BPP µ 2 P and then by symmetry BPP µ 2 P • L 2 BPP: Poly time PTM M: x L Pry[M(x, y) accepts] ≥ 2/3 x L Pry[M(x, y) rejects] ≥ 2/3 • Consider a game between and players • • Need to choose y cooperatively First attempt: • There is a winning strategy for player as long as Pry[M(x, y) accepts] <1 – player wants to prove x L and player wants to prove x L – player chooses ρ 2 {0, 1}n – player chooses t 2 {0, 1}n – Set y = ρ t run M(x, y)

BPP in the Hierarchy • Since game was unfair to player give him several chances – Several (parallel) instances of the game – Force the player to use the same choice in all instances • Second attempt: – player chooses ρ1, … ρm where each ρi 2 {0, 1}n – player chooses t 2 {0, 1}n – Set yi = ρi t run M(x, y 1), M(x, y 2), …, M(x, ym) accept if any of the runs accepts Each ρi invalidates 2/3 rds of possible t 2 {0, 1}n • Invalidates = not a useful response for player • Due to randomization by Xor By a hitting setargument there is a set of ρ1, ρ2, … ρm that invalidates all t 2 {0, 1}n for m= n log 3 2 Happens when bad witnesses But what happens when x L? are a coset of an ECC There might be {ρ1, ρ2, ρ3 } such that [i=1, 2, 3 { t | M(x, y) accepts for y = ρi t} = {0, 1}n Each of size at most 1/3

BPP in the Hierarchy – Can apply error reduction: Poly time PTM M’ • use n’ random bits (|y’| = n’) • fraction of strings y’ for which M’(x, y’) is incorrect is at most 1/n’ Now by the hitting setargument there is a set of ρ1, ρ2, … ρm that invalidates all t 2 {0, 1}n for m= n’ /log n’ But when x L for any choice of {ρ1, ρ2, …, ρm } 1/ 2 n’ |[i=1 m { t | M(x, y) accepts for y = ρi t}| < n’ /log n’ ¢ 1/n’ Each of size at most 1/n’ • Final form – player chooses ρ1, … ρm where each ρi 2 {0, 1}n’ – player chooses t 2 {0, 1}n’ – Set yi = ρi t run M’(x, y 1), M’(x, y 2), …, M’(x, ym) accept if any of the runs accepts clearly a 2 P process

More on BPP in the Hierarchy Simultaneous Provers • To prove BPP ½ 2 P we considered a game between and players – player wants to prove x L and player wants to prove x L • In 2 P setting first makes a move and then player (based on ’s move) What if both players have to move simultaneously? • Want strategy where – player wins whenever x L even if player makes move after player Homework: • Phrase the above requirements in terms of a polynomial time relation R(x, y, z) • Show that for all L BPP such a strategy exists

Polynomial sized circuits for SAT • We know that P = NP implies SAT has poly-sized circuits (SAT P/poly ). – Showing SAT does not have poly-size circuits is a research direction for proving P ≠ NP • Suppose SAT has poly-size circuits – Can we show implies P = NP ? – Instead show: SAT P/poly PH collapses (to second level) • similar implication as if SAT P

Self Reducibility Lemma: If SAT P/poly then there exists a polynomial p(n) and family of circuits C 1, C 2 … such that Cn gets an n sized formula and outputs • A satisfying assignment if is satisfiable • Null if is not satisfiable Corollary: If SAT P/poly and R is polynomial time balanced relation, then for L = { x | z (x, z) 2 R} there is a family of circuits C 1, C 2 … such that L={x| |x|=n implies (x, Cn(x)) 2 R} Can define new polynomial relation R’ such that (x, C) 2 R’ iff (x, C(x))2 R and C is of the right size.

Collapse of The Hierarchy Theorem: if SAT P/poly then PH collapses to the second level. Proof: • Show that 2 P µ Σ 2 P – If L 2 P then we know: L = { x | y z (x, y, z) 2 R } for R P. – “ z (x, y, z) R? ” is in NP – Let Cn be the SAT solver – produces certificate z z (x, y, z) R iff (x, y, Cn(x, y)) R L = { x | Cn y (x, y, Cn(x, y)) 2 R } = { x | Cn y (x, y, Cn) 2 R’ } 2 P

Approximate Counting is in the Hierarchy Theorem: For any f 2 #P there is a g 2 Δ 3 P such that on input x and g(x, ) outputs a (1+ ) approximation to f(x) (1 - )g(x, ) · f(x) · (1+ )g(x, ) Proof: key point – method for proving that sets are certain size The set in question: A = Accept(M(x)) µ {0, 1}m A function f is in #P if there exists a NTM M running in polynomial oftime where M(x) has f(x) accepting paths for all x 2 {0, 1}n

Pair-wise Independent Hash Functions A family of hash functions H={h|h: {0, 1}m {0, 1}ℓ } is pair-wise independentif: for all x ≠ y, for random h 2 RH the random variables h(x), h(y) are uniformly distributed and independent In particular: Pr[h(x)=h(y)]= 1/2ℓ Already saw the approximate version for distributed equality testing Pr[h(x)=h(y)]· Constructing H: • Construction based on matrix multiplication. – Treat x as a m £ 1 vector. – The function is defined by a random m£ ℓ matrix over GF[2]. H={h. A|A 2 GF[2]m£ ℓ and h. A(x)=Ax }

Methods for proving sizes of sets Let H be family of hash functions where for h 2 H h: {0, 1}m {0, 1}ℓ • if h 2 H is 1 -1 on A then clearly |A| · 2ℓ – a bit difficult to expect full uniqueness • Relaxed property: No collisions property if there are h 1, h 2, … hℓ 2 H are such that – for all x 2 A there is an 1 · i · l where for all x’ 2 A{x} we have hi(x) hi(x’) then we know |A| < ℓ 2ℓ Claim: for a pair-wise independent family H, if |A|· 2ℓ-1 , then there exist h 1, h 2, … hℓ 2 H with the no collisions property. Denote with UH(A, ℓ). Claim: for A=Accept(M) we have UH(A, ℓ) 2 Σ 2 P Can eliminate the quantifier on i by explicitly going over all possibilities! Conclusion: with oracles calls to UH(A, ℓ) can find smallest ℓ for which UH(A, ℓ) holds Yields a 2ℓ approximation for f(x) • Can use amplification of f(x) by running M k times (from accepting positions). New machine M will have fk(x) by accepting paths

Proof of No Collisions Claim • For any x 2 A and any x’ 2 A{x} if h is chosen at random from H Pr[h(x)=h(x’)]= 1/2ℓ • By the Union bound Pr[h(x) is unique] ¸ |A| ¢ 1/2ℓ ¸ 1/2 • Hitting set: Construct h 1, h 2, … hℓ one by one, each time covering at least ½ of elements in A that have not been unique so far – Let A’ be the set not covered so far – For any x 2 A’ and any x’ 2 A{x} for random h 2 R H Pr[h(x) is unique] ¸ |A| ¢ 1/2ℓ ¸ 1/2 Note: this is thefull A

Approximate Counting and Uniform Generation • For self reducible problems: – exact counting implies exact uniform generation of witnesses/solutions – Approximate counting: almost uniform generation of solutions Theorem: if P=NP then given Boolean circuit C possible to sample almost uniformly at random satisfying assignment to C

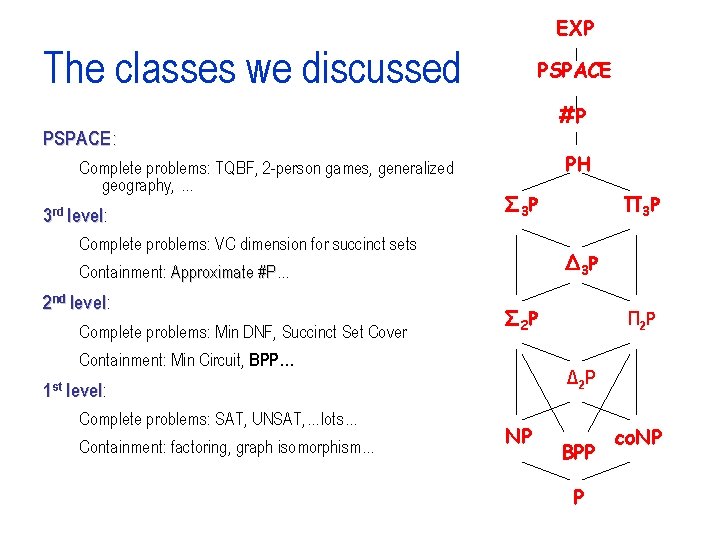
EXP The classes we discussed PSPACE #P PSPACE : Complete problems: TQBF, 2 -person games, generalized geography, … 3 rd level: level PH Σ 3 P Complete problems: VC dimension for succinct sets Δ 3 P Containment: Approximate #P… #P 2 nd level: level Complete problems: Min DNF, Succinct Set Cover Σ 2 P Containment: Min Circuit, BPP… Containment: factoring, graph isomorphism… Π 2 P Δ 2 P 1 st level: level Complete problems: SAT, UNSAT, …lots… Π 3 P NP BPP P co. NP

Some History • • Polynomial Time Hierarchy: Meyer-Stockmeyer BPP in the Hierarchy: Lautmann, Sipser Approximate Counting in the Hierarchy: Stockmeyer SAT P/poly implies collapse: Karp-Lipton, Sipser • Stockmeyer’s papers available: http: //www. geocities. com/stockmeyer@sbcglobal. net/ Survey on problems high in the hierarchy: Schaefer and Umans http: //www. cs. caltech. edu/umans