Complexity Theory Lecture 8 Lecturer Moni Naor Recap

Complexity Theory Lecture 8 Lecturer: Moni Naor

Recap Last week: – – – Randomized Reductions Low memory verifiers #P Completeness of Permanent This Week: – – – Toda’s Theorem: PH P#P. Program checking and hardnesson the average of the permanent Interactive Proofs

Putting the Hierarchy in P#P Toda’s Theorem: PH P#P Idea of the proof: • Characterize PH in terms circuits – a uniformly constructedconstant depth circuit with exponential number of Æ and Ç gates • Consider circuits where the exponentially occurring gates are parity (xor) © – This corresponds to P©P – ©P the class of functions expressible as the number of accepting paths mod 2 in some NTM. • Show to approximate an Æ and an Ç gate using a © gate. – This gives PH RP©P • Show RP©P P#P Tool: -biased probability spaces

Uniformly Direct Connect circuits Let {Cn}n ¸ 1 be a family of circuits. We say that they are Direct Connect Uniformfamily if there is a polynomial time (in n and log the size of Cn) algorithm for the following functions: • TYPE(n, i) – providing the function gate i computes – Can consider various bases. Fan-in of gates can vary Example: Æ , Ç , , Input , Output • IN(n, i, j) – providing k, the jth input into gate i (or none) • OUT(n, i, j) – providing k, the jth output to which gate i (or none) feeds

Characterization of PH in terms of DC Theorem: a language L 2 PH iff it can be computed by a family {Cn}n ¸ 1 of circuits such that • {Cn}n ¸ 1 is Direct Connect Uniform • The gates used are: Æ , Ç , 0(1) • {Cn}n ¸ 1 has constant depth and 2 n size • The gates appear only at the inputs If only Ç gates have exponential fan-in, then this is a characterization of NP key point: we can guess the value of the input as well and consider in the circuit only (x, y) paths that accept. Need to check whether input guess was correct For the PH case, can guess the computation and input as well, need the large fan-in Æ and Ç gates to simulate the alternation

Small bias probability spaces Let be a probability space with K random variables x 1, x 2, … x. K obtaining values in {0, 1}. We say that it is biased if for any subset S µ {1…K} |Pr[ ©i 2 S xi =1] - Pr[ ©i 2 S xi =0]| · A probability space is 0 -biased iff it is the uniform distribution on x 1, x 2, … x. K – Size 2 K Much smaller spaces exists for >0 Description of a point can be O(log (K/ )) Want an efficient way to compute xi from the representation of the point in the sample space. Should be polynomial in log i and the representation of the sample point

A construction for fixed Let K=2ℓ and H={h|h: {0, 1}ℓ } be a family of pairwise independent hash functions Each point in the probability space is defined by • a hash function h 2 R H. – For 1 · j · 1 and 1 · i · K let h_j(i)=1 iff first j bits of h(i) are `0’ and h_j(i)=0 otherwise and • a vector v 1, v 2, … vℓ 2 R {0, 1}ℓ Each xi = © 1 · j · ℓ vj ¢ hj(i) To describe a point in the probability space: Log |H| + log K bits Computation: log K + time to compute h

Analysis of Construction • Let S µ {1…K} and 2 j-2 ≤ |S| ≤ 2 j-1. Event AS = “there is exactly one i 2 S s. t. h_j(i)=1” • We know from unique sat analysis that Prh[AS ]¸ 1/8 Given that AS occurs, for any assignment to v 1, …, vj-1, vj+1 …, vℓ since vj is undetermined we know Pr[ ©i 2 S xi =1]=1/2. • Requirement: for all S µ {1…K} |Pr[ ©i 2 S xi =1] - Pr[ ©i 2 S xi =0]| · Construction: Each xi = © 1 · j · ℓ vj ¢ h_j(i) Conclusion: 1/16 · Pr[ ©i 2 S xi =1] · 1/2 and 1/2 · Pr[ ©i 2 S xi =0] · 15/16 and hence |Pr[ ©i 2 S xi =0] - Pr[ ©i 2 S xi =0]| · 7/8 Can amplify by choosing a few independent constructions and randomly Xoring the assignments

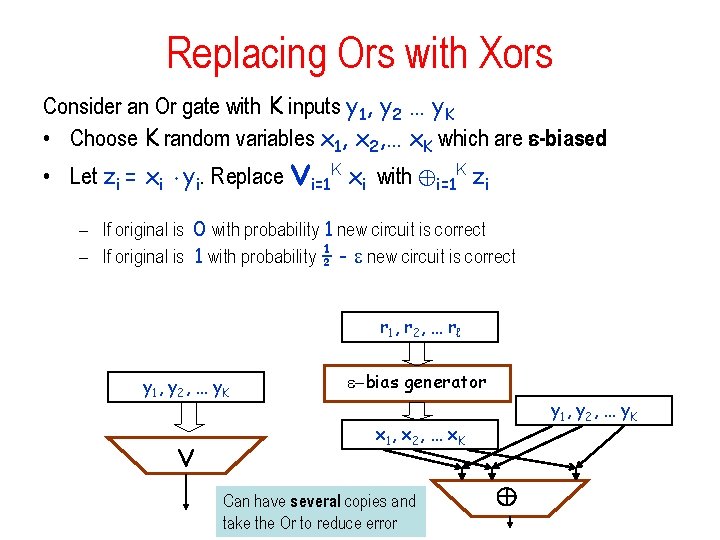
Replacing Ors with Xors Consider an Or gate with K inputs y 1, y 2 … y. K • Choose K random variables x 1, x 2, … x. K which are -biased • Let zi = xi ¢ yi. Replace Çi=1 K xi with ©i=1 K zi – If original is 0 with probability 1 new circuit is correct – If original is 1 with probability ½ - new circuit is correct r 1 , r 2, … r ℓ y 1 , y 2, … y K Ç -bias generator y 1 , y 2, … y K x 1 , x 2, … x K Can have several copies and take the Or to reduce error ©

Replacing Ors with Xors • By repeating the processc nc times can reduce the probability of error to 2 -n – Total number of bits requires is still polynomial in n • If there is a circuit with many Ors – can replace all of them using the same set of random bits simultaneously. – The probability of correct computation is still high • Union bound over the bad events per gate • What about And gates? Turn into Or gates using nots Result: a circuit where only the © gates have exponentially many inputs. The gates are not necessarily at the inputs

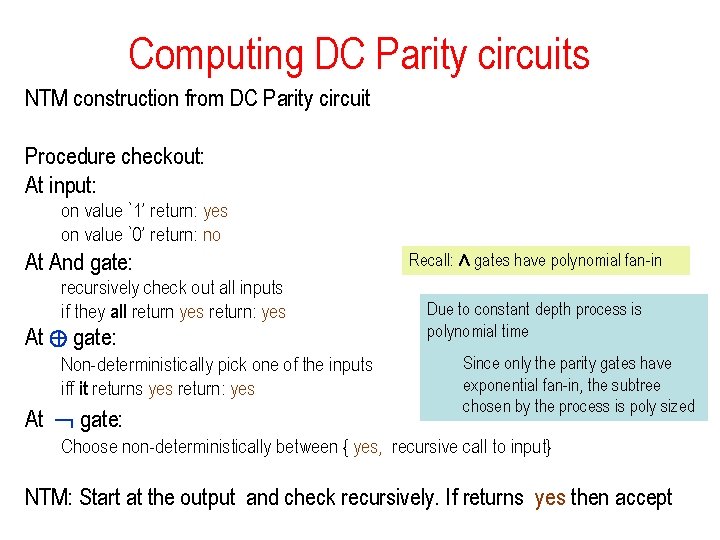
Computing DC Parity circuits Theorem: A family {Cn}n ¸ 1 of circuits such that • {Cn}n ¸ 1 is Direct Connect Uniformusing: © gates with exponential fan-in Æ , Ç , gates with polynomial fan-in • {Cn}n ¸ 1 has constant depth and 2 n can be computed in ©P 0(1) size Proof: need to construct a NTM where the parity of the number of accepting paths equals the circuit value

Computing DC Parity circuits NTM construction from DC Parity circuit Procedure checkout: At input: on value `1’ return: yes on value `0’ return: no At And gate: recursively check out all inputs if they all return yes return: yes At © gate: Non-deterministically pick one of the inputs iff it returns yes return: yes At gate: Recall: Æ gates have polynomial fan-in Due to constant depth process is polynomial time Since only the parity gates have exponential fan-in, the subtree chosen by the process is poly sized Choose non-deterministically between { yes, recursive call to input} NTM: Start at the output and check recursively. If returns yes then accept

PH RP©P and beyond • Given a language L 2 PH consider its DC • Apply the transformation to parity circuits • Apply the transformation from parity circuits to ©P and make the call. Derandomization: RP©P P#P Can consider all random assignments Description is poly-length Based on constructing a gadget that translates Even number of accepting path to 0 Odd number of accepting paths to -1 mod 22 m

EXP The classes we discussed PSPACE #P Time for new classes: • IP PH Σ 3 P • AM[2] • … Π 3 P Δ 3 P Σ 2 P Π 2 P Δ 2 P NP BPP P co. NP

Hardness on the Average of the Permanent • We saw that computing the permanent is #P-Complete – True also for computing it mod M for sufficiently large M • What about random matrices – Can we argue that it is hard to compute per(A) correctly for a random matrix A mod M ? Theorem: if M ¸ n+2 is a prime and • there is a polynomial time algorithm that computes per(A) correctly for a random matrix A mod M with probability at least 1 -1/2 n (over the choice of A), • then there exists a probabilistic polynomial time algorithm for computing per(A) for all matrices A Can replace the 1 -1/2 n with 3/4

Hardness on the Average and Program Correction of Polynomials Let |F|>d+2 and • f: Fn F be a function to which there is oracle access – This is a program that has been implemented • p: Fn F be a polynomial of degree d – This is the function we are really interested in We only have blackbox access to f Sum of the degrees in each monomial • Suppose that f and p agree on a fraction of at least 1 -1/(3 d+3) of their inputs Then we can compute with high probability p(x) for any x 2 Fn Connection to the permanent problem: per(A) is a polynomial of degree n in the n 2 variables corresponding to the entries Can obtain a better result with better correction of errors Reed-Solomon Codes

The randomized reduction • On input x 2 Fn: pick random y 2 R Fn and consider the line ℓ(t) = x + t y. – Each point of ℓ(t) except ℓ(0) is uniformly distributed in Fn • but they are not independent of each other – q(t)=p(ℓ(t)) is a univariate polynomial in t of degree at most d Therefore Pr[p(ℓ(t) =f(ℓ(t)) for all t=1, 2, … d+1] =1 - Pr[9 t 2 {1, 2, … d+1}: p(ℓ(t) ≠ f(ℓ(t))] ¸ 1 –(d+1)/3(d+1) =2/3 If we know q(t)=p(ℓ(t)) at d+1 points, can interpolate to obtain q(0)= p(ℓ(0))= p(x) If we have a good correction procedure for polynomials, then sufficeint to be correct on ¾ of the points.

Consequences • Unlike other NP-Hard problems, cannot expect heuristics that solve many instances • Applications to cryptography? – We are interested in hard on the average problems there, can we use it? – The problem is that these are not solved problems, that come with certificates • What about NP problems, are there such reductions for them? – The simple answer is no, unless the PH collapses • This is a consequence of the classes we are to see next

Program Checking • Let f be a program claiming to perform task T. A checker C for f is a simple program with oracle/black-box access to f and where – If f is good for T, i. e. 8 y f(y)=T(y), then 8 x Cf(x)=T(x) with probability at least 2/3 – If P fails on x, i. e. f(y)≠ T(x), then Pr[Cf(x) accepts f(x)] is at most 1/3 What we just saw: a program checker for the permanent. How about program checker for graph non-isomorphism? How about program checker for SAT? Self reducibility again helpful How about program checker for non-SAT?

Proof systems • What is a “proof”? Complexity theoretic insight: at the minimum a proof should be efficiently verified

Proof systems For a language L, goal is to prove x L General requirements from a Proof system for L: Defined by the verificationalgorithm V – completeness: x L proof, V accepts (x, proof) true assertions have proofs – soundness: x L proof*, V rejects (x, proof*) false assertions have no proofs – efficiency: x, proof, the machine running V(x, proof) us efficient: • runs in polynomial time in |x| • ?

Classical Proofs • Recall: L NP iff expressible as L = { x | y, |y| < |x|k, (x, y) R } and R P. • NP is the set of languages with classical proof systems (R is the verifier) We wish to extend the notion. An extension we have already seen: • two adversarial provers and

Interactive Proofs • Two new ingredients: – Randomness: verifier tosses coins • Should err with some small probability – Interaction: rather than simply “reading” the proof, verifier interacts with prover • Is the prover another TM? • Framework captures the classical NP proof systems: : – prover sends proof. – verifier runs algorithm for R No use of randomness

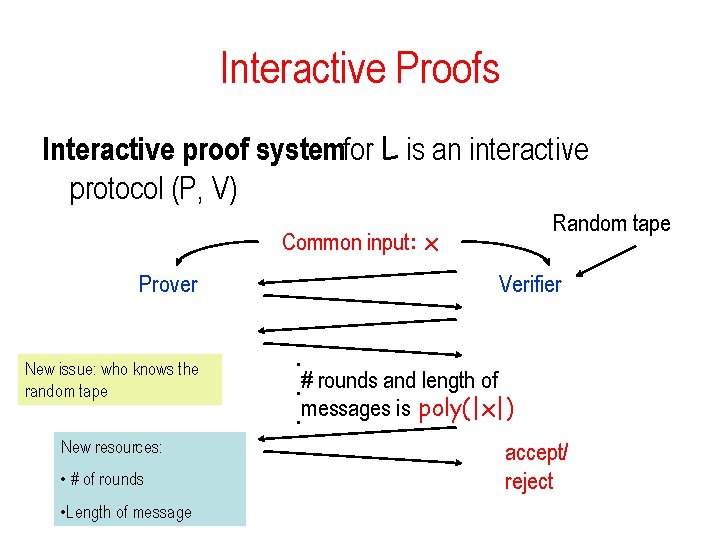
Interactive Proofs Interactive proof systemfor L is an interactive protocol (P, V) Random tape Common input: x Prover New issue: who knows the random tape New resources: • # of rounds • Length of message Verifier. . # rounds and length of. messages is poly(|x|) accept/ reject

Interactive Proofs Definition: an interactive proof systemfor L is an interactive protocol (P, V) Perfect Completeness: V accepts with Prob 1 – completeness: x L: Pr[V accepts in an execution of (P, V)(x)] 2/3 – soundness: x L P* Pr[V accepts in an execution of (P*, V)(x)] 1/3 – efficiency: V is PPT machine • Can we reduce the error to any ?

Error Reduction • If we execute the protocol sequentially ℓ times let Ij =1 if jth run is correct and 0 otherwise The Ij’s are not necessarily independent of each other but, since can tolerate any prover* Pr[Ij =1 | any execution history] ¸ 2/3 If we compare to ℓ independent coins with probability 2/3 where we take majority of answers For any prover* the interactive proof stochastically dominates • Can argue the same for ℓ parallel executions Number of rounds is preserved Things are not so simple when: • More than one prover • Prover is assumed to be efficient

Interactive Proofs New complexity class: IP = {L : L has an interactive proof system} – Captures more broadly what it means to be convinced that a statement is true • But no certificate to store for future generations! – Clearly NP µ IP. Potentially IP larger. • How much larger? – IP with perfect soundnessand completeness is NP • To go beyond NP randomness is essential • Perfect soundness in itself implies NP power

Famous Example: Graph Isomorphism Two graphs G 0 = (V, E 0) and G 1 = (V, E 1) are isomorphic(G 0 G 1) if there exists a permutation π: V V for which (x, y) E 0 (π(x), π(y)) E 1

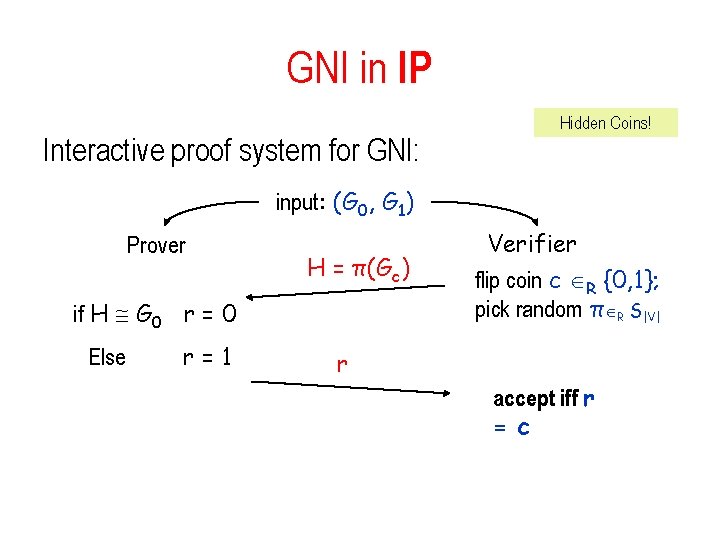
Graph Isomorphism • The problem GI = {(G 0, G 1) : G 0 G 1 } – Is in NP – But not known to be in P, or to be NP-complete • One of Karp’s original open problems in famous NP-Completeness paper • GNI = complement of GI – not known to be in NP Theorem: GNI IP – Was first indication IP may be more powerful than NP

GNI in IP Interactive proof system for GNI: Hidden Coins! input: (G 0, G 1) Prover H = π(Gc) if H G 0 r = 0 Else r=1 Verifier flip coin c R {0, 1}; pick random π R S|V| r accept iff r = c

GNI in IP • Completeness: – if G 0 is not isomorphic to G 1, then H is isomorphic to exactly one of (G 0, G 1) Perfect Completeness: V – prover will always choose correct r accepts with Prob 1 • Soundness: – if G 0 G 1 then the distributionson H in case c = 0 and c = 1 are identical – Hence: no information on c • Any prover P* can succeed with probability exactly ½. Hidden coins seem essential – but as we will see can obtain a protocol with public coins only.

Lack of certificate Bug or feature? Disadvantages clear, but: • Advantage: proof remains `property’ of prover and not automatically shared with verifier • Very important in cryptographic applications – Zero-knowledge • Many variants • Can be used to transform any protocol designed to work with benign players into one working with malicious ones – The computational variant is useful for this purpose • Can be used to obtain (plausible) deniability

Code Equivalence Problem • For two k £ n matrices G 1 and G 2 over finite field F we way that they are equivalent if there is – A k £ k matrix S which is non singular over F – An n £ n permutation matrix P Such that G 1 =SG 2 P This means that if we think of the codewords generated by G 1 and G 2, then there is a 1 -1 mapping after reordering the bit positions c=x. G Code word Information word Homework: Show that the non-equivalent of matrices problem is in IP with constant number of rounds

The power of IP • GNI IP suggests IP more powerful than NP, since GNI not known to be in NP • GNI is in co. NP Today: • co. NP µ P#P µ IP • IP µ PSPACE Theorem: IP=PSPACE

IP µ PSPACE Optimal strategy for prover: • Strategy: for input x, at each step given the interaction so determine the next message. • Optimal strategy for x: the one yielding the best probability of acceptance by V Claim: Optimal strategy is computable in PSPACE

References • Toda’s Theorem: Toda, FOCS 1989 • Progam Checking: Blum and Kannan, Blum, Luby and Rubinfeld • Average Hardness of permanent: Lipton 1990 – Polynomials – Beaver and Feigenbaum, 1990 • Interactive Proof system: – Public coins version: Babai 1985 (Babai, Moran) – Private Coins: Goldwasser Micali and Rackoff • Proof system for GNI: Goldreich, Micali and Wigderson, 1986 • Private coins equals public coins: Goldwasser and Sipser, 1986