Complexity Theory Lecture 9 Lecturer Moni Naor Recap

Complexity Theory Lecture 9 Lecturer: Moni Naor

Recap Last week: Toda’s Theorem: PH P#P. Program checking and hardness on the average of the permanent Interactive Proofs – – – • Proof for graph non-isomorphism This Week: IP=PSPACE Start with #P in PSPACE Public vs. Private Coins IP[k]=AM Mechanism for showing non NP-Completeness

Interactive Proofs Definition: an interactive proof systemfor L is an interactive protocol (P, V) Perfect Completeness: V accepts with Prob 1 – completeness: x L: Pr[V accepts in an execution of (P, V)(x)] 2/3 – soundness: x L P* Pr[V accepts in an execution of (P*, V)(x)] 1/3 – efficiency: V is PPT machine We can reduce the error to any

Lack of certificate Bug or feature? Disadvantages clear, but: • Advantage: proof remains `property’ of prover and not automatically shared with verifier • Very important in cryptographic applications – Zero-knowledge Honest verifier perfect zero-knowledge • Many variants • Can be used to transform any protocol designed to work with benign players into one working with malicious ones – The computational variant is useful for this purpose • Can be used to obtain (plausible) deniability

The power of IP Last week • GNI 2 IP • IP µ PSPACE Today: • co. NP µ P#P µ IP and Theorem: IP=PSPACE

Idea of the Protocol for #SAT Idea: think of the rush hour protocol Input: (x 1, x 2, …, xn) – prover: “ has k satisfying assignments” – true iff • ( x 1=0, x 2, …, xn) has k 0 satisfying assignments • ( x 1=1, x 2, …, xn) has k 1 satisfying assignments • k = k 0 + k 1 – prover sends k 0, k 1 – verifier sends random c R {0, 1} – prover recursively proves “ ( x 1=c, x 2, …, xn) has kc satisfying assignments” – at the end of the protocol, verifier can check for itself.

Protocol analysis • Completeness: if (x 1, x 2, …, xn) has k satisfying assignments – accept with Prob. 1 • Soundness: if (x 1, x 2, …, xn) does not have k satisfying assigns. – accept with Prob at most 1 – 2 -n – At the recursive call prover must cheat regarding at least one of k 0 or k 0 • Prob ½ of choosing the `correct’ one – Have to be correct on any recursive call: 2 -n

Decreasing the Probability of Cheating • Solution to problem: – replace {0, 1}n with (Fq)n – verifier substitutes random field element at each step – vast majorityof field elements catch cheating prover* (rather than just 1 out of 2) Theorem: L = {( , k): CNF has exactly k satisfying assignments} is in IP In particular can prover non-sat (k=0)

Arithmetizationof Transform (x 1, x 2, …, xn) into polynomial P (x 1, x 2, … xn) of degree d over a field Fq where q is a prime > 2 n – recursively: • xi • (1 - P ) • ’ (P )(P ’) • ’ 1 - (1 - P )(1 - P ’) Claim: for all x {0, 1}n we have P (x) = (x) – degree d | | Can compute P (x 1, x 2, … xn) in poly time from and x 1, x 2, … xn

The Interactive protocol for counting • Prover wishes to prove: k = Σx 1 = 0, 1Σx 2 =0, 1 … Σxn = 0, 1 P (x 1, x 2, … xn) • Define: kz = Σx 2 =0, 1 … Σxn = 0, 1 P (x 1=z, x 2, … xn) Suppose prover sends: kz for all z Fq To perform the computation mod q we • verifier: – Check the consistency: need q>2^n • that k 0 + k 1 = k • Answers are consistent with a polynomial in z – Send random z Fq • continue with proof that kz = Σx 2 = 0, 1 … Σxn = 0, 1 P (x 1=z, x 2, … xn) • At the end: verifier checks for itself

The Interactive protocol for counting • Prover wishes to prove: k = Σx 1 = 0, 1Σx 2 = 0, 1 … Σxn = 0, 1 P (x 1, x 2, … xn) • Define: kz = Σx 2 = 0, 1 … Σxn = 0, 1 P (x 1=z, x 2, … xn) • How to send kz for all z Fq ? • Solution: send the univariate polynomial in z! – recall degree d | |

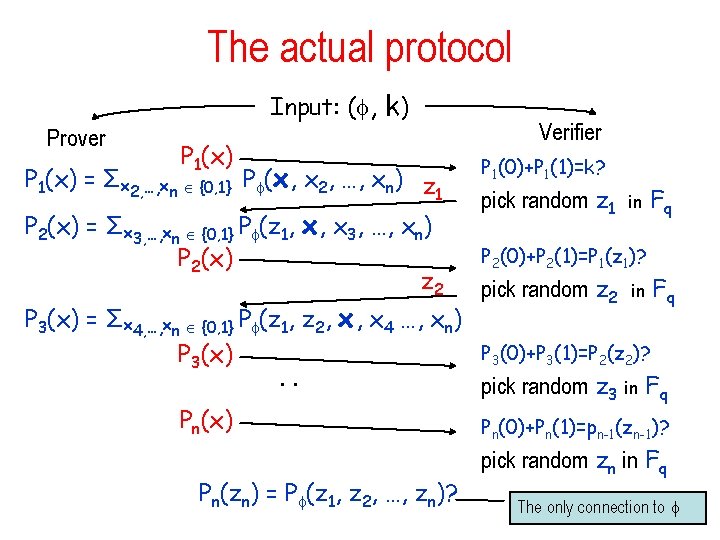
The actual protocol Input: ( , k) Prover P 1(x) = Σx 2, …, xn {0, 1} P (x, x 2, …, xn) z 1 P 2(x) = Σx 3, …, xn {0, 1} P (z 1, x, x 3, …, xn) P 2(x) z 2 Verifier P 1(0)+P 1(1)=k? pick random z 1 in P 2(0)+P 2(1)=P 1(z 1)? pick random z 2 in Fq Fq P 3(x) = Σx 4, …, xn {0, 1} P (z 1, z 2, x, x 4 …, xn) P 3(0)+P 3(1)=P 2(z 2)? P 3(x). . pick random z 3 in Fq Pn(x) Pn(0)+Pn(1)=pn-1(zn-1)? Pn(zn) = P (z 1, z 2, …, zn)? pick random zn in Fq The only connection to

Analysis of protocol • Completeness: – if ( , k) L then the (honest) prover always makes the verifier accept • By inspection

Soundness Analysis – let Pi(x) be the correct polynomials – let Pi*(x) be the polynomials actually sent by a (cheating) prover At first step: ( , k) L P 1(0) + P 1(1) ≠ k • Either P 1*(0) + P 1*(1) ≠ k (and V rejects) • or P 1* ≠ P 1 Prz 1[P 1*(z 1) = P 1(z 1)] d/q | |/2 n At each step i, assume Pi(zi) ≠ Pi*(zi) • either Pi+1*(0) + Pi+1*(1) ≠ Pi*(zi) (and V rejects) • or Pi+1* ≠ Pi+1 Przi+1[Pi+1*(zi+1) = Pi+1(zi+1)] | |/2 n

Analysis of protocol • Soundness (continued): – if verifier does not reject, there must be some i for which: Pi* ≠ Pi and yet Pi*(zi) = Pi(zi) – for each i, probability is | |/2 n Union bound: probability that there exists an i for which the bad event occurs is at most n| |/2 n poly(n)/2 n << 1/3

Extending the protocol to TQBF Given a TQBF 9 x 1 8 x 2 9 x 3 … 8 xn (x 1, x 2, …, xn) can transform (x 1, x 2, …, xn) into a polynomial P (x 1, x 2, … xn). Now the problem is to prove: k = Σx 1 = 0, 1 x 2 =0, 1 Σx 3 = 0 … Σxn = 0, 1 P (x 1, x 2, … xn) > 0 First attempt: repeat the same protocol with checking multiplication at the right places Problem: multiplication increases the degree After n step the degree might be 2 n Solution: since we are only interested in the {0, 1} values, can approximate the polynomial with a multi-linear function. New operator Rxi for linearization Rxi [p(x 1, x 2, …, xn )]=(1 -x 1) p(0, x 2, …, xn )+ x 1 p(1, x 2, …, xn )

The TQBF Protocol Given a TQBF 9 x 1 8 x 2 9 x 3 … 8 xn (x 1, x 2, …, xn) transform (x 1, x 2, …, xn) into a polynomial P (x 1, x 2, … xn). and transform 9 x 1 8 x 2 9 x 3 … 8 xn into 9 x 1 Rx 1 8 x 2 Rx 1 Rx 2 9 x 3 Rx 1 Rx 2 Rx 3 … 8 xn Rx 1 Rx 2 Rx 3 … Run the protocol as before, but in rounds corresponding to Rxi use Rxi [p(x 1, x 2, …, xn )]=(1 -x 1) p(0, x 2, …, xn )+ x 1 p(1, x 2, …, xn ) to reduce the degree. The polynomials remain linear. Theorem: IP = PSPACE

Public Coins Arthur-Merlin Games • Definition of IP permits the verifier to keep its coin-flips private – necessary feature? – The Graph Non-Isomorphism protocol we saw breaks without it New characters: Arthur as the verifier and Merlin as the prover • Arthur-Merlin (Art. Mer ) game: interactive protocol in which coinflips are public – Arthur (verifier) may as well just send the results of coin-flips. No point in doing any computation until the final step • If more complicated computation are need, Merlin (prover) can perform by himslef any computation Arthur would have done – Merlin does not know in advance the coin flips

Arthur and Merlin

Arthur-Merlin Games • Clearly Art. Mer µ IP – private (secret) coins are at least as powerful as public coins. Can release them when the right time comes • The TQBF protocol (proof that IP = PSPACE) actually shows PSPACE µ Art. Mer µ IP µ PSPACE – public coins are as powerful as private coins! • When the number of rounds is not bounded!

Arthur-Merlin Games • Limiting the # of rounds: – AM[k] = Arthur-Merlin game with k rounds, Arthur (verifier) goes first – MA[k] = Arthur-Merlin game with k rounds, Merlin (prover) goes first We will see: Theorem: AM[k] (MA[k]) equals AM[2] (MA[2] ) with perfect completeness.

Perfect Completeness of Arthur Merlin Games Theorem: If L 2 AM[k], then L 2 MA[k+1]. I. e. has a k+1 round protocol with perfect completeness Proof: think of the BPP ½ PH proof Run m games simultaneously Make sure probability of error in each game is smaller than 1/3 m Preliminary round Merlin: gives shifts ρ1, … ρm Each ρj is sufficiently long to cover the coins for all k rounds ρj = ρj 1 ρj 2 …ρjk In each round Arthur : chooses in each round 1 · i · k a set of coins ri the m games are played in the ith round with coins (ri © ρ1 i , ri © ρ2 i , …, ri © ρmj ) Arthur : accepts if any of the m games accepts m has to large enough to contain a hitting setfor all r 1, r 2, …rk

Collapse of Arthur-Merlin Games Theorem: for all constant k 2 AM[k] = AM[2]. • Proof: – Will show MA[2] AM[2] – The same argument can be used to move all of Arthur’s messages to the beginning of interaction: AMAMAM…AM=AAMMAM…AM… = AAA…AMMM…M

Equivalent definition of MA and AM with perfect completeness Definitions without reference to interaction: – L MA iff poly-time relation R x L m Prr[(x, m, r) R] = 1 x L m Prr[(x, m, r) R] ½ – L AM iff poly-time language R x L Prr[ m (x, m, r) R] = 1 x L Prr[ m (x, m, r) R] ½ Even easier to reduce the error to any

MA[2] AM[2] Given L MA[2] x L m Prr[(x, m, r) R] = 1 Prr[ m (x, m, r) R] = 1 order reversed x L m Prr[(x, m, r) R] ε Prr[ m (x, m, r) R] 2|m|ε – Need to reduce the error ε < 2 -ℓ. – By repeating ℓ =|m|+1 times with independent random strings r get 2|m| ε < ½. Homework: what happens to the time analysis when repeated k times?

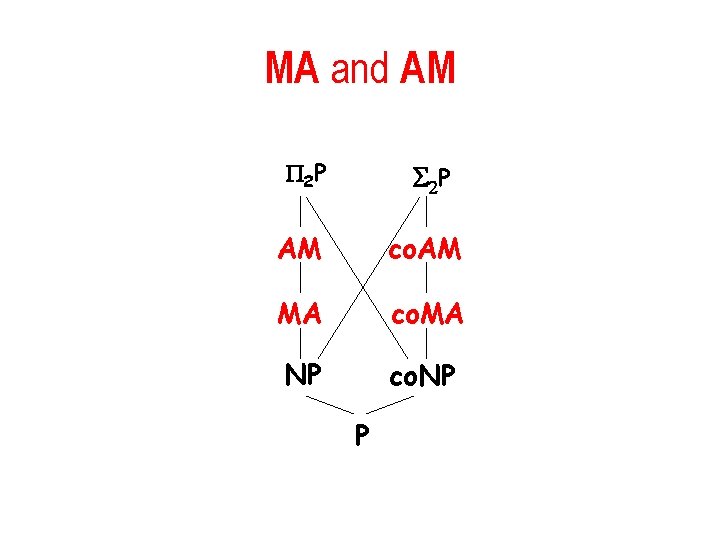
MA and AM • Two important classes: – MA = MA[2] – AM = AM[2] We saw MA µ AM Confusion alert: when talking about AM is it the unbounded version or AM[2]? Not all the literature is consistent

MA and AM Relation to other complexity classes: • both MA and AM contain NP • can choose to not use randomness at all • both MA and AM contained in 2 P L 2 P iff R P for which: x L Prr[ m (x, m, r) R] = 1 x L Prr[ m (x, m, r) R] < 1 – so AM µ 2 P We know that MA AM

MA and AM Theorem: if co. NP µ AM then PH = AM and the hiereachy collapses. Proof: co. NP µ AM means that there is an AM protocol for any poly relation R for proving (if true) for a given x the statement z (x, z) R Suffices to show Σ 2 Pµ AM (and use the fact AM µ Π 2 P) – L Σ 2 P iff poly-time relation R x L y z (x, y, z) R The AM protocol for x L: – Merlin sends y – Run an AM protocol for proving for (x, y) that z (x, y, z) R Altogether an MAM protocol. MAM =AM µ Π 2 P

MA and AM 2 P S 2 P AM co. AM MA co. MA NP co. NP P

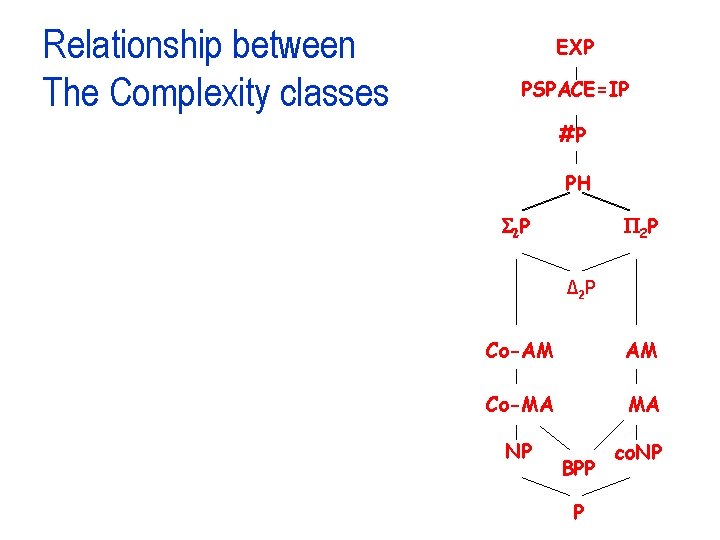
Relationship between The Complexity classes EXP PSPACE=IP #P PH S 2 P Δ 2 P Co-AM AM Co-MA MA NP co. NP BPP P

Public vs Private Coins in constant number of rounds • We know Art. Mer = IP. – public coins = private coins Definition: IP[k]={L|L has a k round IP protocol} Theorem: IP[k] µ AM[O(k )] – implies for all constant k 2, IP[k] = AM[O(k )] = AM[2] • So in particular: GNI IP[2] = AM

Public coins protocol for GNI Want to prove that (G 0, G 1) 2 GNI Idea: use the size of set protocol we have already seen The set in question is the number of transcripts that make the verifier accept For a graph G let aut(G)={ | (G)=G} Assume for simplicity but with loss of generality that |aut(G 0)|=|aut(G 1)|=1 Let S={H| H G 0 or H G 1}. Then – If G 0 G 1 we have that |S|=n! – Else |S|=2 n! Can amplify the gap to 2 m by m repetition In general S={(H, )| H G 0 or H G 1 and 2 aut(H)}.

Size of set protocol • Want to prove that S is large. – Suppose S µ U – Let H be a pairwise independent hash function h 2 H maps elements in U in {0, 1}ℓ Arthur: choose h 2 R H Merlin: find x 2 S such that h(x)= 0ℓ If |S| ¸ 2ℓ If then Prh[9 x 2 S such that h(x)=0ℓ ] ¸ 1/2 Use inclusion-exclusion and the pairwise independence of events h(x)=0ℓ and h(x’)=0ℓ If |S| < 1/100 ¢ 2ℓ then Prh[9 x 2 S such that h(x)= 0ℓ ] < 1/100 In general: if |S| ¸ 2 k ¢ 2ℓ then Prh[9 x 2 S s. t. h(x)=0ℓ ] ¸ 1 - 2 -k And if |S|· 2 -k ¢ 2ℓ then Prh[9 x 2 S s. t. h(x)=0ℓ ]· 2 -k

Implications to Graph Isomorphism It is not known whether GI is NP-complete. – Conclusion from previous Theorems: if GI is NP-complete then PH = AM – does not seem likely! Proof: GI being NP-complete means that GNI is co. NPcomplete co. NP AM PH = AM

A mechanism for showing non-hardness of problems • By placing a problem in AM Å Co-AM one demonstrates that the problem is not NP-Complete according to the current world view • Alternatively, one can view it as a method for showing impossibility of certain types of protocols

Random Self Reductions • Definition: A non-adaptive random self reduction for a function f is a probabilistic algorithm C such that on input x – C produces y 1, y 2, yk 2 {0, 1}m and – Given f(y 1), f(y 2 ), f(yk), C computes f(x) We require the following – Each of the yi‘s is uniformly distributed in {0, 1}m • There may be dependence between the yi‘s – All sizes (k, m) are polynomial – The probability of successfully computing f(x) given correct answers to f(y 1), f(y 2 ), f(yk) is large for any input x Example: the permanent

Random Self Reduction and NPCompleteness Theorem: if any NP-Complete language has a nonadaptive random self reduction, then PH collapses to the third level. The function we are interested in is f(x)=1 if x 2 L and f(x)=0 otherwise Proof: Need some non-uniformity: the fraction m of {y 2 {0, 1}m |f(y) 2 L} This value cannot be negligible, or NP µ BPP

The AM Protocol • If f(x)=1 then x 2 L and since L 2 NP there is a proof • If f(x)=0 then run ℓ times in parallel: Verifier: use C to produce y 1, y 2, yk 2 {0, 1}m Prover: send f(y 1), f(y 2), f(yk) • for each yi, such that f(y 1)=1 add NP proof Verifier: Verify the NP proofs for f(y 1)=1. Run C on result to obtain f(x) Global test: make sure that the fraction of yi such that f(yi)=0 in all ℓ executions is roughly m Accept if all test are verified and all the executions conclude that f(x)=0 Conclusion: cannot expect such a reduction for an NP-Complete problem

Difference in distribution generated by circuits For a circuit C with n inputs and m outputs call the distribution on {0, 1}m of C(x) when x 2 R {0, 1}n the distribution generatedby C. Given two circuits C 1 and C 2 we would like to check whether these two distributions are close or far from each other. The variation distance(or statistical difference) between distribution D 1 and D 2 on universe U is V(D 1, D 2)= max. S µ U |Pr. D [x 2 S] – Pr. D [x 2 S]|. 1 2 The VD( , ) Problem: Separate the cases • V(D 1, D 2) · • V(D 1, D 2) ¸ when D 1 and D 2 are the distributions generated by C 1 and C 2.

Homework Show that if the Graph Isomorphism problem is not in BPP, then there is no probabilistic polynomial time algorithm that solves VD(0, 1) Show an AM protocol for VD(0, 1). For distributions D 1 and D 2 let S 1={x | Pr. D [x] > Pr. D [x ]} 1 2 and S 2={x | Pr. D [x] > Pr. D [x ]} 2 1 Show: V(D 1, D 2)= x 2 U Pr. D [x 2 S 1] - Pr. D [x 2 S 1]= x 2 U Pr. D [x 2 S 2] - Pr. D [x 2 S 2] 1 2 2 Show an AM protocol for distinguishing the general case, i. e. VD( , ). What is the complexity of the protocol as a function of - ? 2

References • Average Hardness of permanent: Lipton 1990 • Interactive Proof system: – Public coins version: Babai 1985 (Babai, Moran) – Private Coins: Goldwasser Micali and Rackoff • Proof system for GNI: Goldreich, Micali and Wigderson, 1986 • Private coins equals public coins: Goldwasser and Sipser, 1986 • Proof system for #P: Lund, Fortnow, Karloff and Nisan • Proof system for PSPACE: Shamir • Impossibility of non-adaptive random self reductions: Feigenbaum and Fortnow