Foundations of Cryptography Lecture 11 Lecturer Moni Naor

Foundations of Cryptography Lecture 11 Lecturer: Moni Naor

Recap of Lecture 10 • • • Pseudo-randomness of subset sum Composing pseudo-random generators Hybrid arguments The next-bit test Pseudo-random functions

Next-bit Test Definition: a function g: {0, 1}* → {0, 1}* is said to pass the next bit test if • It is polynomial time computable • It stretches the input |g(x)|>|x| – denote by ℓ(n) the length of the output on inputs of length n • If the input (seed) is random, then the output passes the next-bit test For any prefix 0≤ i< ℓ(n), for any probabilistic polynomial time adversary A that receives the first i bits of y= g(x) and tries to guess the next bit, or any polynomial p(n) and sufficiently large n |Prob[A(yi, y 2, …, yi)= yi+1] – 1/2 | < 1/p(n) Theorem: a function g: {0, 1}* → {0, 1}* passes the next bit test if and only if it is a pseudo-random generator

Next-block Undpredictable Suppose that the function G maps a given a seed into a sequence of blocks G: S y 1 y 2, … , let ℓ(n) be the length of the number of blocks given a seed of length n • If the input (seed) is random, then the output passes the next-block unpredicatability test For any prefix 0≤ i< ℓ(n), for any probabilistic polynomial time adversary A that receives the first i blocks of y= g(x) and tries to guess the next block yi+1, for any polynomial p(n) and sufficiently large n |Prob[A(y 1, y 2, …, yi)= yi+1] | < 1/p(n) Homework: show to convert a next-block unpredictable generator into a pseudo-random generator.

Pseudo-Random Generators concrete version Gn: 0, 1 m 0, 1 n A cryptographically strong pseudo-random sequence generator - if passes all polynomial time statistical tests (t, )-pseudo-random - no test A running in time t can distinguish with advantage

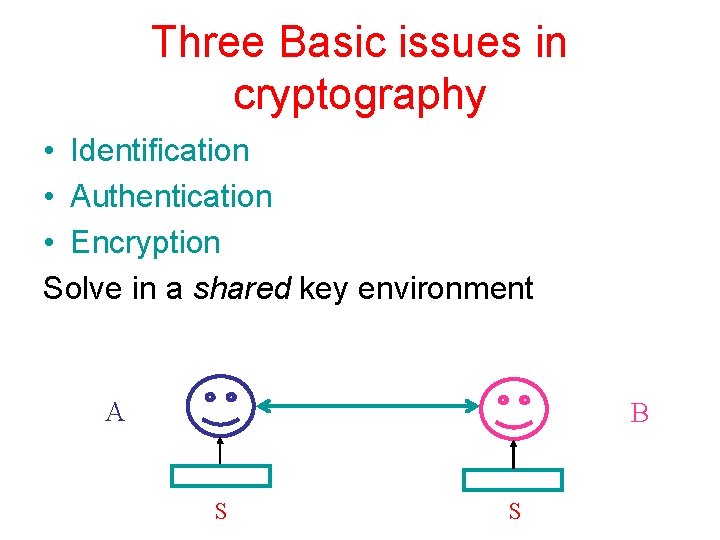
Three Basic issues in cryptography • Identification • Authentication • Encryption Solve in a shared key environment A B S S

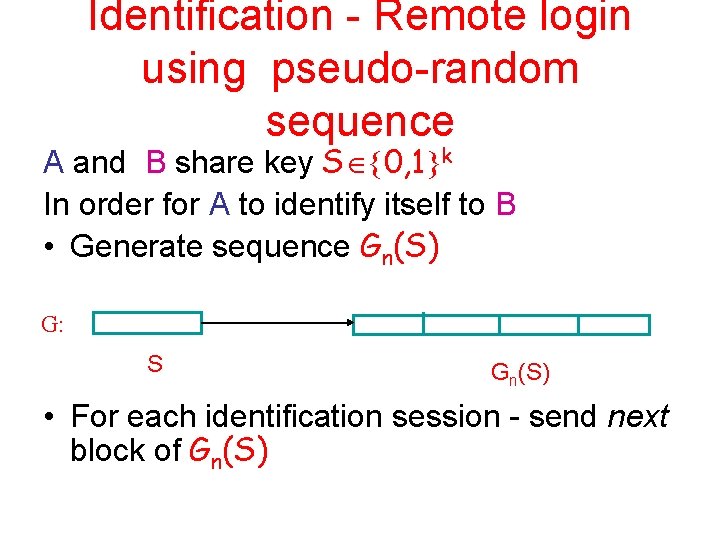
Identification - Remote login using pseudo-random sequence A and B share key S 0, 1 k In order for A to identify itself to B • Generate sequence Gn(S) G: S Gn(S) • For each identification session - send next block of Gn(S)

Problems. . . • • More than two parties Malicious adversaries - add noise Coordinating the location block number Better approach: Challenge-Response

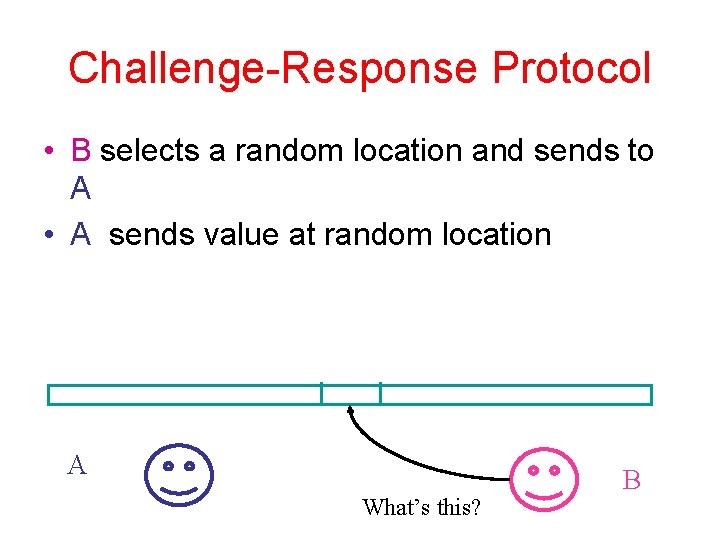
Challenge-Response Protocol • B selects a random location and sends to A • A sends value at random location A What’s this? B

Desired Properties • Very long string - prevent repetitions • Random access to the sequence • Unpredictability - cannot guess the value at a random location – even after seeing values at many parts of the string to the adversary’s choice. – Pseudo-randomness implies unpredictability • Not the other way around for blocks

Authenticating Messages • A wants to send message M 0, 1 n to B • B should be confident that A is indeed the sender of M One-time application: S (a, b) - where a, b R 0, 1 n To authenticate M: supply a. M b Computation is done in GF[2 n]

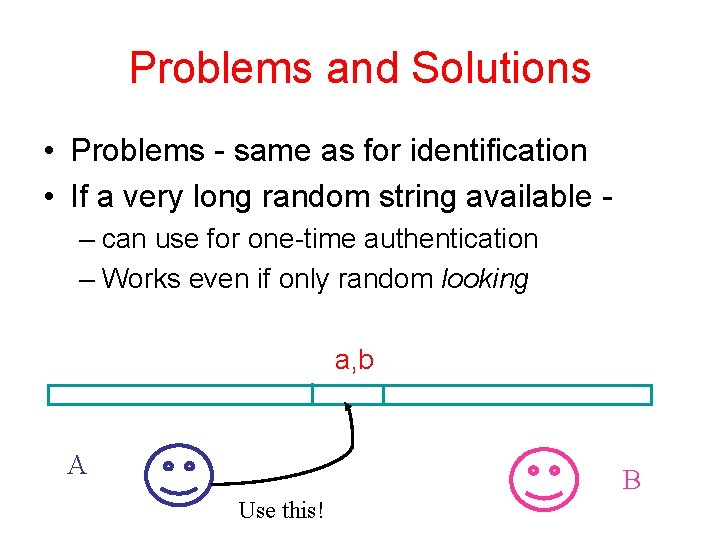
Problems and Solutions • Problems - same as for identification • If a very long random string available – can use for one-time authentication – Works even if only random looking a, b A B Use this!

Encryption of Messages • A wants to send message M 0, 1 n to B • only B should be able to learn M One-time application: S a - where a R 0, 1 n To encrypt M send a M

Encryption of Messages • If a very long random looking string available – can use as in one-time encryption A B Use this!

Pseudo-random Functions Concrete Treatment: F: 0, 1 k 0, 1 n 0, 1 m key Domain Range Denote Y= FS (X) A family of functions Φk ={FS | S 0, 1 k is (t, , q)-pseudo-random if it is • Efficiently computable - random access and. . .

(t, , q)-pseudo-random The tester A that can choose adaptively – X 1 and get Y 1= FS (X 1) – X 2 and get Y 2 = FS (X 2 ) … – Xq and get Yq= FS (Xq) • Then A has to decide whether – FS R Φk or – FS R R n m = F | F : 0, 1 n 0, 1 m

(t, , q)-pseudo-random For a function F chosen at random from (1) Φk ={FS | S 0, 1 k (2) R n m = F | F : 0, 1 n 0, 1 m For all t-time machines A that choose q locations and try to distinguish (1) from (2) Prob A ‘ 1’ F R Fk - Prob A ‘ 1’ F R R n m

Equivalent/Non-Equivalent Definitions • Instead of next bit test: for X X 1, X 2 , , Xq chosen by A, decide whether given Y is – Y= FS (X) or – Y R 0, 1 m • Adaptive vs. Non-adaptive • Unpredictability vs. pseudo-randomness • A pseudo-random sequence generator g: 0, 1 m 0, 1 n – a pseudo-random function on small domain 0, 1 log n 0, 1 with key in 0, 1 m

Application to the basic issues in cryptography Solution using a shared key S Identification: B to A: X R 0, 1 n A to B: Y= FS (X) A verifies Authentication: A to B: Y= FS (M) replay attack Encryption: A chooses X R 0, 1 n A to B: <X , Y= FS (X) M >

Goal • Construct an ensemble {Φk | k L such that • for any {tk, 1/ k, qk | k L polynomial in k, for all but finitely many k’s Φk is a (tk, k, qk )-pseudo-random family

Construction • Construction via Expansion – Expand n or m • Direct constructions

Effects of Concatenation Given ℓ Functions F 1 , F 2 , , Fℓ decide whether they are – ℓ random and independent functions OR – FS 1 , FS 2 , , FSℓ for S 1, S 2 , , Sℓ R 0, 1 k Claim: If Φk ={FS | S 0, 1 k is (t, , q)-pseudorandom: cannot distinguish two cases – using q queries – in time t’=t - ℓ q – with advantage better than ℓ

Proof: Hybrid Argument • i=0 • i=ℓ FS 1 , FS 2 , , FSℓ … R 1, R 2 , , Ri-1, FSi+1 , , FSℓ … R 1, R 2 , , R ℓ pℓ - p 0 i pi+1 - pi /ℓ p 0 pi pℓ

. . . Hybrid Argument Can use this i to distinguish whether – FS R Φk or FS R R n m • Generate FSi+1 , , FSℓ • Answer queries to first i-1 functions at random (consistently) • Answer query to FSi , using (black box) input • Answer queries to functions i+1 through ℓ with FSi+1 , , FSℓ Running time of test - t’ ℓ q

Doubling the domain • Suppose F(n): 0, 1 k 0, 1 n 0, 1 m which is (t, , q)-p. r. • Want F(n+1): 0, 1 k 0, 1 n+1 0, 1 m which is (t’, ’, q’)-p. r. Use G: 0, 1 k 0, 1 2 k which is (t , ) p. r G(S) G 0(S) G 1(S) Let FS (n+1)(bx) FGb(s) (n)(x)

Claim If G is (t q, 1)-p. r and F(n) is (t 2 q, 2, q)-p. r, then F(n+1) is (t, 1 2 2, q)-p. r Proof: three distributions (1) F(n+1) (2) FS 0 (n) , FS 1 (n) for independent S 0, S 1 (3) Random 1 2 2 D

. . . Proof Given that (1) and (3) can be distinguished with advantage 1 2 2 , then either • (1) and (2) with advantage 1 – G can be distinguished with advantage 1 or • (2) and (3) with advantage 2 2 – F(n) can be distinguished with advantage 2 Running time of test - t’ q

Getting from G to F(n) Idea: Use recursive construction FS (n)(bnbn-1 b 1) FGb (s) (n-1)(bn-1 bn-2 b 1) 1 Gb (S)) ) n n-1 1 Each evaluation of FS (n)(x): n invocations of G

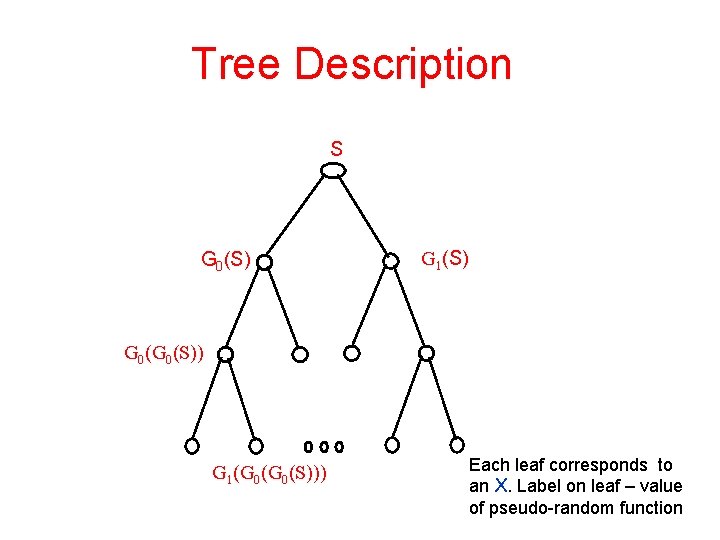
Tree Description S G 0(S) G 1(S) G 0(S)) G 1(G 0(S))) Each leaf corresponds to an X. Label on leaf – value of pseudo-random function

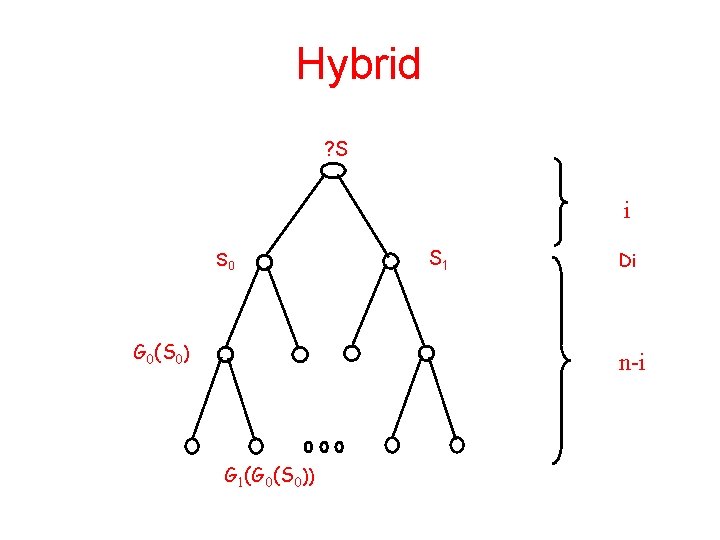
Security claim If G is (t qn , ) p. r, then F(n) is (t, ’ n q , q) p. r Proof: Hybrid argument by levels Di : – truly random labels for nodes at level i. – Pseudo-random from i down Each Di - a collection of q functions i pi+1 - pi ’/n q

Hybrid ? S i S 0 G 0(S 0) S 1 Di n-i G 1(G 0(S 0))

…Proof of Security • Can use this i to distinguish concatenation of q sequence generators G from random. • The concatenation is (t, q ) p. r Therefore the construction is (t, , q) p. r

Disadvantages • Expensive - n invocations of G • Sequential • Deterioration of But does the job! From any pseudo-random sequence generator construct a pseudo-random function. Theorem: one-way functions exist if and only if pseud-random functions exist.

Applications of Pseudo-random Functions • Learning Theory - lower bounds – Cannot PAC learn any class containing pseudo-random function • Complexity Theory - impossibility of natural proofs for separating classes. • Any setting where huge shared random string is useful • Caveat: what happens when the seed is made public?

Application to Signatures • Shared secret seed - can get authentication • What about public-key? Can we use the techniques? • Yes!? – Private key is S – Public key is commitment to FS – To sign M - provide FS(M) and a proof of consistency with the commitment

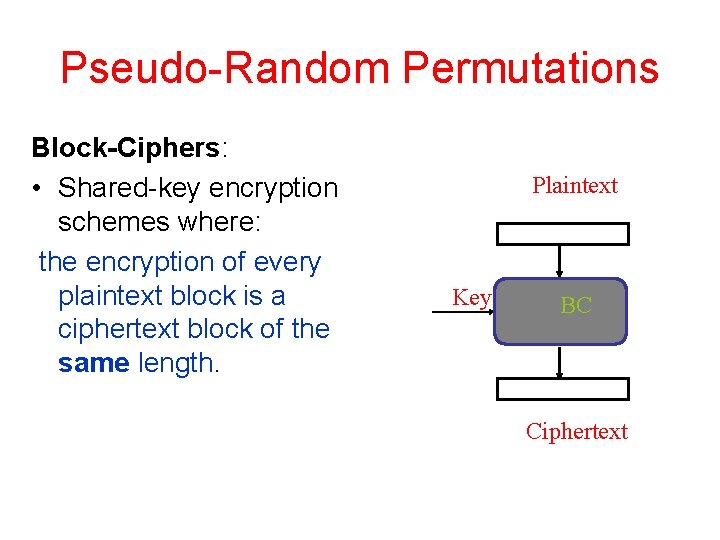
Pseudo-Random Permutations Block-Ciphers: • Shared-key encryption schemes where: the encryption of every plaintext block is a ciphertext block of the same length. Plaintext Key BC Ciphertext

Block Ciphers Advantages – Saves up on memory and communication bandwidth – Easy to incorporate within existing systems. Main Disadvantage – Every block is always encrypted in the same way. • Important Examples: DES, AES

Modeling Block Ciphers • Pseudo-random Permutations F : 0, 1 k 0, 1 n Key Domain F-1: 0, 1 k 0, 1 n Key Range Want: – X= FS-1 (FS (X)) • Correct inverse – Efficiently computable 0, 1 n Range 0, 1 n Domain

The Test The tester A that can choose adaptively – X 1 and get Y 1= FS (X 1) – Y 2 and get X 2= FS-1(Y 2) … – Xq and get Yq= FS (Xq) • Then A has to decide whether – F S R Φk Can choose to evaluate or invert any point! or – FS R P(n) = F | 1 -1 F : 0, 1 n

(t, , q)-pseudo-random For a function F chosen at random from (1) Φk ={FS | S 0, 1 k (n) (2) P = F | 1 -1 F : 0, 1 n For all t-time machines A that choose q locations and try to distinguish (1) from (2) Pr A= ‘ 1’ F R Fk (n) - Pr A= ‘ 1’ F R P

Construction of Pseudo. Random Permutations • Possible to construct p. r. permutation from p. r. functions (and vice versa. . ) • Based on 4 Feistal Permutations

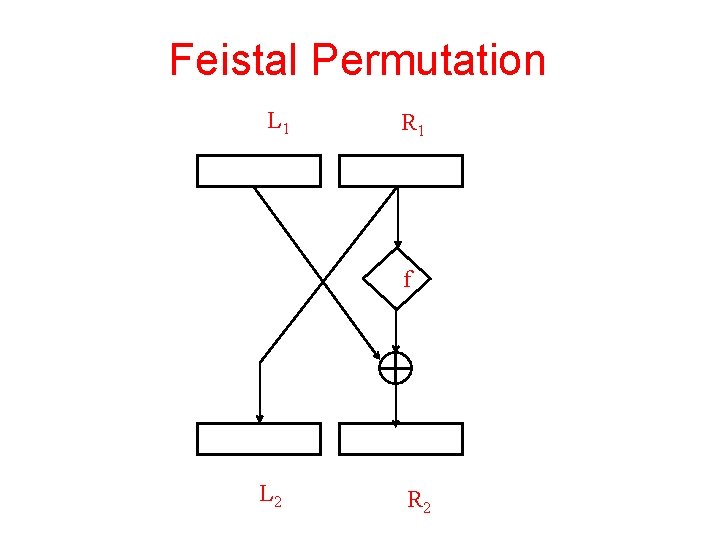
Feistal Permutation Any f : 0, 1 n defines a Feistal Permutation Df(L, R)=(R, L f(R)) Feistal permutations are as easy to invert as to compute: Df-1(L, R)=(R f(L), L) Many Block Cipher based on such permutations where the function f is derived from secret key

Feistal Permutation L 1 R 1 f L 2 R 2

Composing Feistal Permutations • Make the function f: 0, 1 n a pseudo-random function FS R Φk = {FS | S 0, 1 k • This defines a keyed family of permutations 0, 1 2 n • Clearly it is not pseudo-random – Right block goes unchanged to left block What about composing two such keyed permutations With independent keys • Not pseudo-random: DS 2(DS 1(L, R)= (FS 1(L) R, FS 2(FS 1(L) R) -For two inputs sharing the same left block • Looks pretty good for random attacks!

Main Construction Let F 1, F 2 , F 3 , F 4 R PRF, then the composition of DF 1 , DF 2 , DF 3 , DF 4 is a pseudo-random permutation. • Each Fi : 0, 1 n Resulting Permutation 0, 1 2 n. • F 1 and F 4 can be ``combinatorial”: – pair-wise independent. – low probability of collision on first block • Error probability is ~ q 2/2 n

References • Blum-Micali : SIAM J. Computing 1984 • Yao: • Blum, Shub: SIAM J. Computing, 1988 • Goldreich, Goldwasser and Micali: J. of the ACM, 1986 • Luby-Rackoff: SIAM J. Computing, 1988 • Naor-Reingold: Journal of Cryptology,

. . . References • O. Goldreich, The Foundations of Cryptography - a book in preparation, www. wisdom. weizmann. ac. il/~oded/foc-book. html • M. Luby, Pseudorandomness and Cryptographic Applications, Princeton University Press. • S. Goldwasser and M. Bellare Lecture Notes on Cryptography, www-cse. ucsd. edu/~mihir/papers/gb. html