Cryptography and Sudoku Moni Naor WEIZMANN INSTITUTE OF

Cryptography and Sudoku Moni Naor WEIZMANN INSTITUTE OF SCIENCE Joint work with: מוני נאור Ronen Gradwohl, Benny Pinkas, Guy Rothblum

What is Cryptography? Traditionally: how to maintain secrecy in communication Alice and Bob talk while Eve tries tolisten Bob Alice Eve

Cryptography § Very ancient occupation Biblical times: Atbash in Jeremiah איך נלכדה ששך ותתפש תהלת כל הארץ איך היתה לשמה בבל בגויים § Egyptian Hieroglyphs § Unusual ones. . . § Many interesting books and sources, especially about the Enigma (WW 2)

Modern Times §The Up. Study to the 70’s: classified military ofofmid the needed to solvework Prevalence theresources Internet: § computational problems is in the news (daily!) § • Cryptography Exception: Shannon, Turing* • Cryptography is relevant to ``everyone” - security and Since then - explosive growth privacy issues for individuals § Commercial applications § Scientific work: tight relationship with Computational Complexity Theory § Major works: Diffie-Hellman, Rivest, Shamir and Adleman (RSA) § Recently: more involved models for more diverse tasks. How to maintain the secrecy, integrity and functionality in computer and communication system.

Computational Complexity Theory § Study the resources needed to solve computational problems § Computer time A computational problem: § Computer memory • multiplying two numbers, § Communication • selecting a move in a chess position § Parallelism • Find the shortest tour visiting all cities § Randomness § … § Identify problems that are infeasible to compute by any reasonable machine § Taxonomy: classify problems into classes with similar properties wrt the resource requirements § Help find the most efficient algorithm for a problem P=NP?

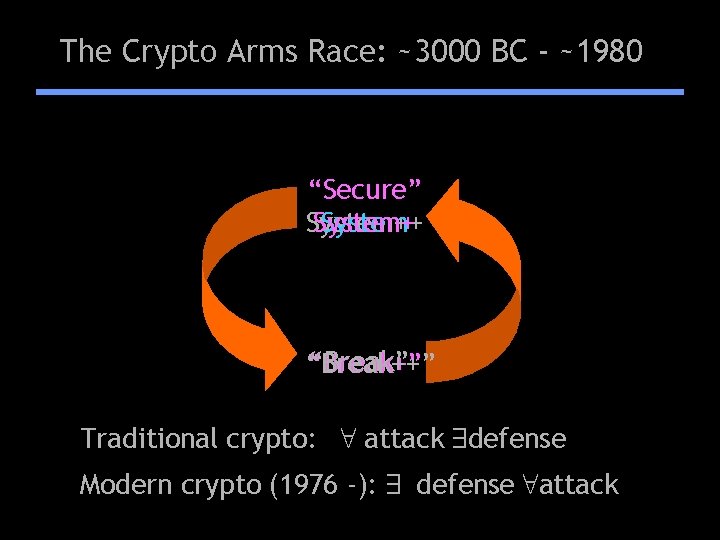
The Crypto Arms Race: ~3000 BC - ~1980 “Secure” System++ System “Break” “Break++” “Break+” Traditional crypto: 8 attack 9 defense Modern crypto (1976 -): 9 defense 8 attack

Sudoku § Fill in the empty entries in the grid so that every row, every column, and every 3 x 3 subgrid contains the digits 1 through 9.

Sudoku § Fill in the empty entries in the grid so that every row, every column, and every 3 x 3 subgrid contain the digits 1 through 9. § Can be generalized to an n n grid, where n=k 2. § The size of an instance is O(n 2 log(n)) bits. § Nothing special about the numbers 1… 9.

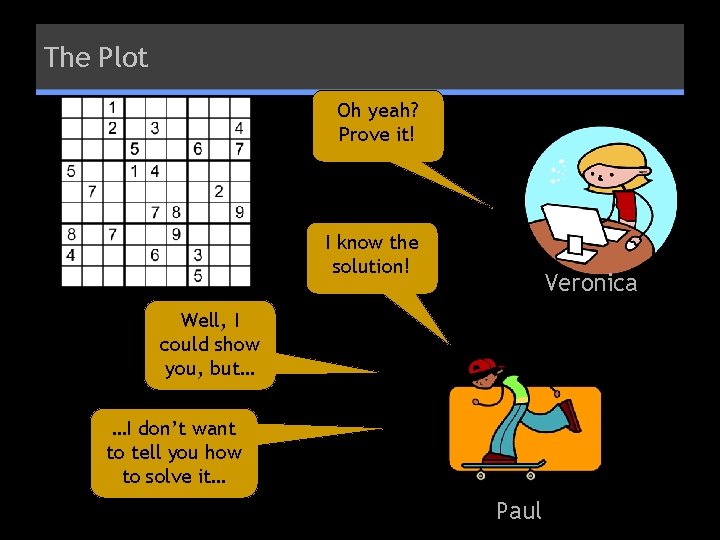
The Plot Oh yeah? Prove it! I know the solution! Veronica Well, I could show you, but… …I don’t want to tell you how to solve it… Paul

Zero-Knowledge Proofs Paul wants to prove that “A is true” Blah? Blah! Oh! If “A is true”: Veronica is convinced, but doesn’t learn about A! She can’t prove that “A is true”.

Why Study Zero-Knowledge Proofs? § Authentication: prove your identity to someone using secret information, without revealing the secret § Force malicious adversaries to act according to protocol Design protocol with benign adversaries. Then compile to withstand malicious ones § Why study zero-knowledge for Sudoku? § It has nice properties § It’s educational – everybody knows Sudoku § It’s FUN!

Outline § Definitions § Physical model § A basic protocol § 2 variations

Interactive Proof § Probabilistic protocol between 2 parties: Prover and Verifier § Both know instance of a problem § Prover might know a witness/solution § Players “chat”, and at the end, verifier accepts or rejects § Completeness: probability that honest verifier accepts correct proof § Soundness error: probability that verifier accepts incorrect proof

Zero-Knowledge Proof § Interactive Proof § Zero-knowledge property: Whatever Verifier learned from Prover, could have learned by himself § Exists efficient Simulator that can simulate conversation, without access to Prover § zero-knowledge proof for all NP § Proof of 3 -colorability Set of problems that § Proof for Hamiltonicity have efficient verification

Sudoku and Complexity § Sudoku is in NP § Means: easy to verify solutions § In fact: Sudoku is NP Complete – not all that relevant § There are zero-knowledge proofs for all problems in NP § Therefore there is a ZK proof for Sudoku. § Direct ZK proofs for Sudoku are preferable: § Efficiency: avoiding the overhead of the reduction § Practicality: Implementable without the aid of computers § Understandability (by non-experts!): Ensure that participants have intuitive understanding of the proof.

Physical Objects § Typical Cryptographic metaphor: § Physical “locked box” § Hard to find physical locked box that: § Can never be opened § Are readily available § Have transparent operation § Tamper-evident seal § Tampering is evident § Can open, but can’t reseal § Scratch-off card, sealed envelope

Scratch-Off Cards § Can’t tell them apart (until unsealed) § Can shuffle them effectively § Like picking a random permutation § Can triplicate them § Stronger requirement § Used in perfect soundness protocol

Human Behavior § Paul and Veronica are in same room § Shuffling: Paul wants a fair shuffle, Veronica wants to make sure no cards were switched § More benign adversary: § Either protocol works, or cheating player is labeled a “cheater”

Playing Cards § Can use playing cards instead of scratch-off cards: § Sealing = turning card face down § Revealing = turning it face up § Not really tamper evident § Works when players in same room, watching each other

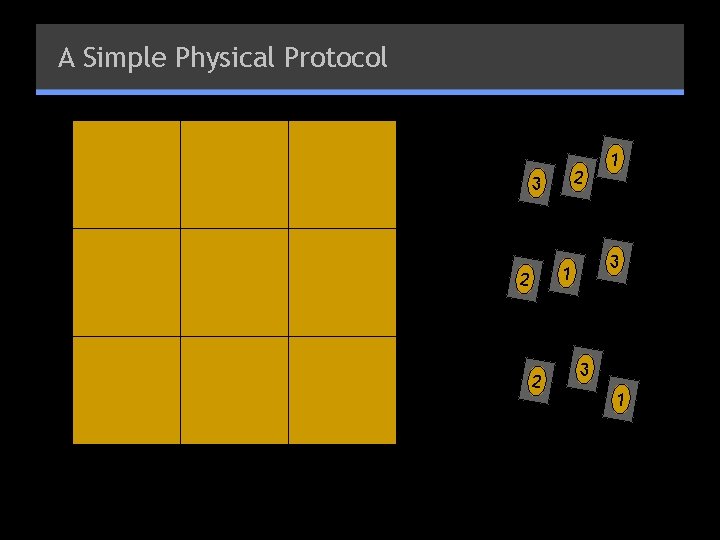
A Simple Physical Protocol Flip coin: rows or columns?

A Simple Physical Protocol 2 3 3 1 2 2 1 3 1

A Simple Physical Protocol § Props: 81 sealed scratch-off cards, and a board with 81 cells (like Sudoku) § P places a sealed card on each cell § Corresponding to his solution § “filled-in” values are unsealed § V chooses one of rows/cols/subgrids § P makes packet for each row, shuffles it § V takes each packet, unseals cards, verifies that each contains cards 1… 9 § If yes -- accept, otherwise reject

Analysis § Completeness: perfect § Soundness: cheating P must cheat in one of rows, columns, or subgrids § P is caught with probability ≥ 1/3 § Zero-knowledge: V only sees some permuted values of 1… 9

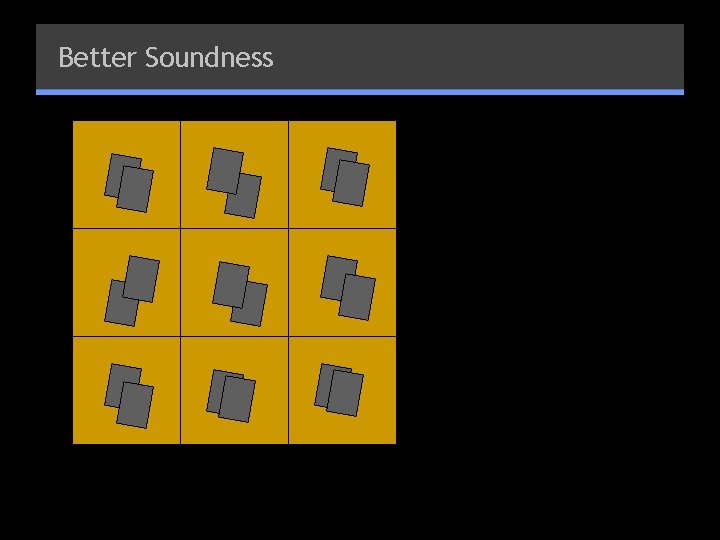
Better Soundness

Better Soundness 2 3 2 1 1 2 2 3 3 1 2 1 3 1

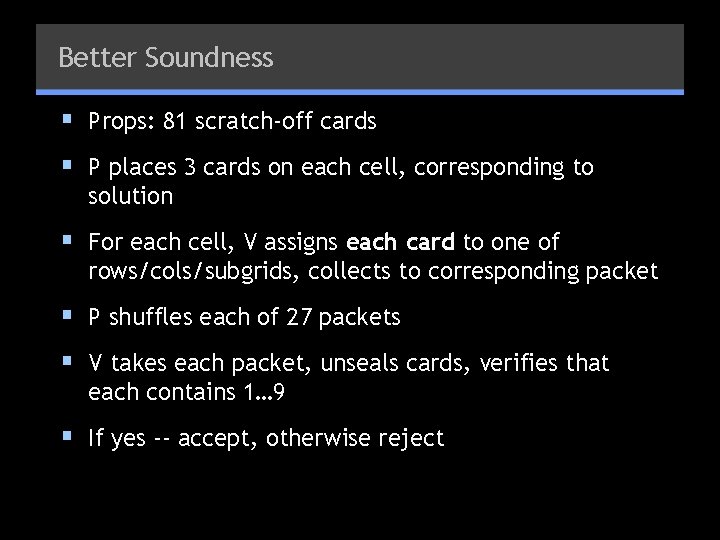
Better Soundness § Props: 81 scratch-off cards § P places 3 cards on each cell, corresponding to solution § For each cell, V assigns each card to one of rows/cols/subgrids, collects to corresponding packet § P shuffles each of 27 packets § V takes each packet, unseals cards, verifies that each contains 1… 9 § If yes -- accept, otherwise reject

Analysis of Soundness § P can no longer cheat as before § New way to cheat: 3 cards on a cell are not the same value § Say some cell gets 3 values, not all the same. § One of three cards is different from others § Belongs to one of rows/cols/subgrids § o/w P is always caught cheating § V assigns card to correct row/col/subgrid with probability at most 1/3 ⇒ Cheating P caught with probability 2/3 § Actually: can show that P is caught with probability 8/9 § At least 2 cells are mislabeled § o/w P is always caught cheating

Reducing Number of Shuffles § Previous protocol required 27 shuffles. Too much! § New protocol: same as before – § 3 cards on each cell § V assigns each to row/col/subgrid § Make 27 packets § For each packet, V assigns a random number 1…c § For each i, P assembles all packets with number i § P shuffles each of c piles § V takes each pile, unseals cards, verifies that each contains correct number of cards 1… 9. § If yes -- accept, otherwise reject

Analysis § Only c shuffles required § Soundness: § With probability 8/9, some packet j is unbalanced § However, two unbalanced packets, if shuffled together, may balance each other § Suppose all packets except j are assigned to one of c piles § If piles are balanced, then assigning j will cause imbalance ⇒ P will be caught § If 2+ piles are unbalanced ⇒ P will be caught § If 1 pile is unbalanced, j will balance it only if assigned to it, with probability 1/c ⇒ Cheating P is caught with probability 8(c-1)/9 c

Perfect Soundness § If 3 cards on each cell are guaranteed to have same value, cheating P would always get caught! § Implementing triplicate: § With trusted setup: 3 cards (with same value) are connected and can be torn apart § Without trusted setup: § Use colors instead of numbers § Each card is a circle, prepared by P § V cuts each card into 3 equal pieces (randomly) 3 3 3 § If card was not uniformly colored, random cut will reveal nonuniformity when card is scratched

Perfect Soundness with a trusted copy machine: Prepare three copies of the solution. § Puzzle should be printed on the back. § One copy is cut along the rows § One copy is cut along the columns § One copy is cut along the subgrids § Each strip is then cut into cells § The cells are shuffled (or sorted by the prover) § Verifier checks that § all values 1… 9 are there § The “filled-in” cells have the same values on both sides § To prove that the correct puzzle was solved

Cryptographic Protocols ALICE BOB Protocols Encryption Zero-knowledge proofs Authentication Secure computation Digital signatures Assumptions needed: existence of a one-way function Cryptographic protocols: proceed by exchanging digital message

Open problems: § Implement physical protocol over the mail? Parties need not be in the same room § Possible to implement commitments from scratch-off cards. § However, an amplification stage requires many repetitions § Not easy for humans § Other puzzles?

Cryptography Today phlegmon of the pharynx

Cryptography Today Cryptography is a very active research area § Research activities range: § providing firm foundations § Relationship with complexity theory § providing actual constructions and analysis for specific needs. Some recent topics § Obfuscation of programs § Maintaining privacy of released data § Voting Schemes

Any questions?

Based on: § R. Gradwohl, M. Naor, B. Pinkas and G. Rothblum, Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles, FUN 2007. Available: www. wisdom. weizmann. ac. il/~naor/ PAPERS/ sudoku_abs. html