Structure Learning in Bayesian Networks Eran Segal Weizmann

Structure Learning in Bayesian Networks Eran Segal Weizmann Institute

Structure Learning Motivation n Network structure is often unknown n Purposes of structure learning n Discover the dependency structure of the domain n Goes beyond statistical correlations between individual variables and detects direct vs. indirect correlations Set expectations: at best, we can recover the structure up to the Iequivalence class Density estimation n Estimate a statistical model of the underlying distribution and use it to reason with and predict new instances

Advantages of Accurate Structure X 1 Spurious edge X 1 X 2 Y Missing edge X 1 X 2 Y § Increases number of fitted parameters § Cannot be compensated by parameter estimation § Wrong causality and domain structure assumptions

Structure Learning Approaches n Constraint based methods n n View the Bayesian network as representing dependencies Find a network that best explains dependencies Limitation: sensitive to errors in single dependencies Score based approaches n View learning as a model selection problem n n Define a scoring function specifying how well the model fits the data Search for a high-scoring network structure Limitation: super-exponential search space Bayesian model averaging methods n n Average predictions across all possible structures Can be done exactly (some cases) or approximately

Constraint Based Approaches n Goal: Find the best minimal I-Map for the domain n G is an I-Map for P if I(G) I(P) n n n Minimal I-Map if deleting an edge from G renders it not an I-Map G is a P-Map for P if I(G)=I(P) Strategy n n Query the distribution for independence relationships that hold between sets of variables Construct a network which is the best minimal I-Map for P

Constructing Minimal I-Maps n Reverse factorization theorem n n G is an I-Map of P Algorithm for constructing a minimal I-Map n n Fix an ordering of nodes X 1, …, Xn Select parents of Xi as minimal subset of X 1, …, Xi-1, such that Ind(Xi ; X 1, …Xi-1 – Pa(Xi) | Pa(Xi)) Limitations (Outline of) Proof of minimal I-map n § Independence involve a above large number variables n I-map since queries the factorization holds byofconstruction n Minimal since by construction, removing one edge destroys § Construction involves a large number of queries (2 i-1 subsets) the factorization § We do not know the ordering and network is sensitive to it

Constructing P-Maps n Simplifying assumptions n n Network has bound in-degree d per node Oracle can answer Ind. queries of up to 2 d+2 variables Distribution P has a P-Map Algorithm n n n Step I: Find skeleton Step II: Find immoral set of v-structures Step III: Direct constrained edges

Step I: Identifying the Skeleton n For each pair X, Y query all Z for Ind(X; Y | Z) n n X–Y is in skeleton if no Z is found If graph in-degree bounded by d running time O(n 2 d+2) n n Since if no direct edge exists, Ind(X; Y | Pa(X), Pa(Y)) Reminder n If there is no Z for which Ind(X; Y | Z) holds, then X Y or Y X in G* n n Proof: Assume no Z exists, and G* does not have X Y or Y X Then, can find a set Z such that the path from X to Y is blocked Then, G* implies Ind(X; Y | Z) and since G* is a P-Map Contradiction

Step II: Identifying Immoralities n For each pair X, Y query candidate triplets X, Y, Z n n X Z Y if no W is found that contains Z and Ind(X; Y | W) If graph in-degree bounded by d running time O(n 2 d+3) n n If W exists, Ind(X; Y|W), and X Z Y not immoral, then Z W Reminder n If there is no W such that Z is in W and Ind(X; Y | W), then X Z Y is an immorality n n n Proof: Assume no W exists but X–Z–Y is not an immorality Then, either X Z Y or X Z Y exists But then, we can block X–Z–Y by Z Then, since X and Y are not connected, can find W that includes Z such that Ind(X; Y | W) Contradiction

Answering Independence Queries n Basic query n n n Determine whether two variables are independent Well studied question in statistics Common to frame query as hypothesis testing n n n Null hypothesis is H 0: Data was sampled from P*(X, Y)=P*(X)P*(Y) Need a procedure that will Accept or Reject the hypothesis n 2 test to assess deviance of data from hypothesis n Alternatively, use mutual information between X and Y

Structure Based Approaches n Strategy n n n Define a scoring function for each candidate structure Search for a high scoring structure Key: choice of scoring function n n Likelihood based scores Bayesian based scores

Likelihood Scores n Goal: find (G, ) that maximize the likelihood n n Score. L(G: D)=log P(D | G, ’G) where ’G is MLE for G Find G that maximizes Score. L(G: D)

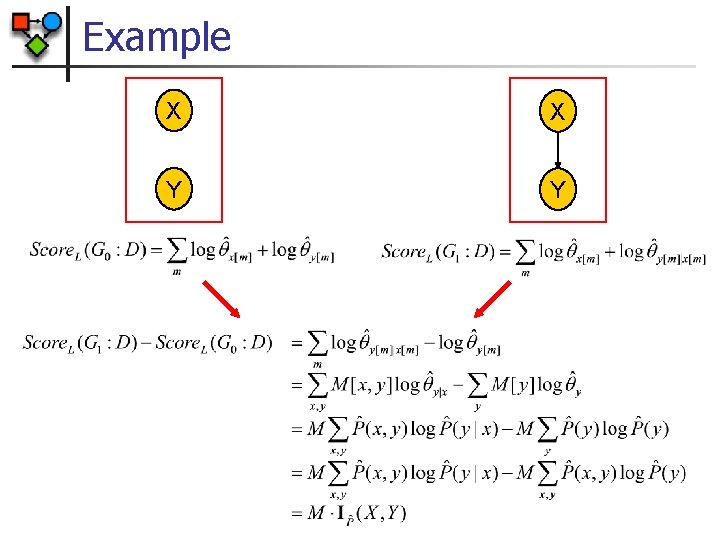
Example X X Y Y

General Decomposition n The Likelihood score decomposes as: n Proof:

General Decomposition n The Likelihood score decomposes as: n n n Second term does not depend on network structure and thus is irrelevant for selecting between two structures Score increases as mutual information, or strength of dependence between connected variable increases After some manipulation can show: n To what extent are the implied Markov assumptions valid

Limitations of Likelihood Score X X Y Y G 0 G 1 § Since IP(X, Y) 0 Score. L(G 1: D) Score. L(G 0: D) § Adding arcs always helps § Maximal scores attained for fully connected network § Such networks overfit the data (i. e. , fit the noise in the data)

Avoiding Overfitting n Classical problem in machine learning n Solutions n Restricting the hypotheses space n n n Minimum description length n n n Limits the overfitting capability of the learner Example: restrict # of parents or # of parameters Description length measures complexity Prefer models that compactly describes the training data Bayesian methods n n Average over all possible parameter values Use prior knowledge

Bayesian Score Marginal likelihood Prior over structures Marginal probability of Data P(D) does not depend on the network Bayesian Score:

Marginal Likelihood of Data Given G Bayesian Score: Likelihood Prior over parameters Note similarity to maximum likelihood score, but with the key difference that ML finds maximum of likelihood and here we compute average of the terms over parameter space

Marginal Likelihood: Binomial Case n Assume a sequence of m coin tosses By the chain rule for probabilities n Recall that for Dirichlet priors n n Where Mm. H is number of heads in first m examples

Marginal Likelihood: Binomial Case Simplify using (x+1)=x (x) For multinomials with Dirichlet prior

Marginal Likelihood Example Actual experiment with P(H) = 0. 25 -0. 6 -0. 7 (log P(D)) / M n -0. 8 -0. 9 -1 Dirichlet(. 5, . 5) Dirichlet(1, 1) Dirichlet(5, 5) -1. 1 -1. 2 -1. 3 0 5 10 15 20 25 M 30 35 40 45 50

Marginal Likelihood: Bayes. Nets n Network structure determines form of marginal likelihood 1 2 3 4 5 6 7 X H T T H H Y H T H H T T H Network 1: Two Dirichlet marginal likelihoods P(X[1], …, X[7]) P(Y[1], …, Y[7]) Network X Y

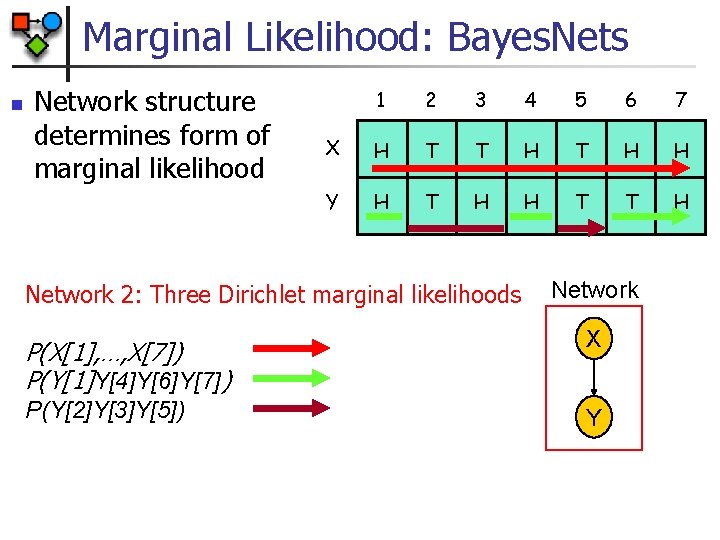
Marginal Likelihood: Bayes. Nets n Network structure determines form of marginal likelihood 1 2 3 4 5 6 7 X H T T H H Y H T H H T T H Network 2: Three Dirichlet marginal likelihoods Network P(X[1], …, X[7]) P(Y[1]Y[4]Y[6]Y[7]) X P(Y[2]Y[3]Y[5]) Y

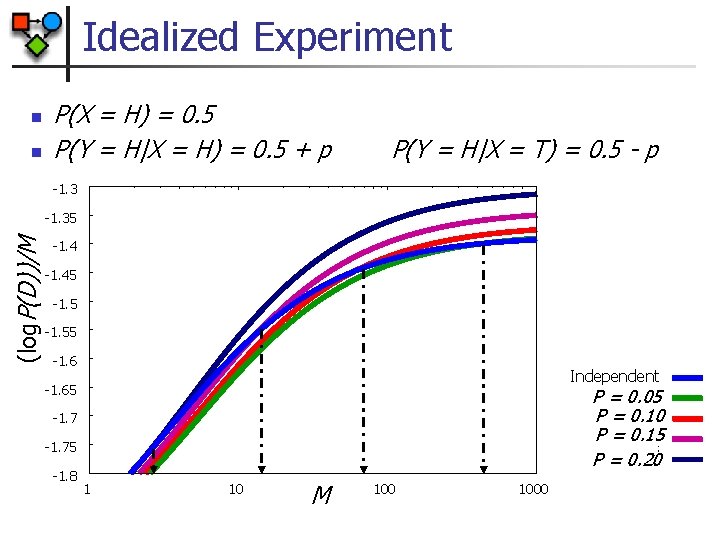
Idealized Experiment n n P(X = H) = 0. 5 P(Y = H|X = H) = 0. 5 + p P(Y = H|X = T) = 0. 5 - p -1. 3 (log. P(D))/M -1. 35 -1. 45 -1. 55 -1. 6 Independent -1. 65 P = 0. 05 P = 0. 10 P = 0. 15 P = 0. 20 -1. 75 -1. 8 1 10 M 1000

Marginal Likelihood: Bayes. Nets The marginal likelihood has the form: where n n Dirichlet Marginal Likelihood For the sequence of values of Xi when Xi’s parents have a particular value M(. . ) are the counts from the data (. . ) are hyperparameters for each family

Priors Bayesian Score: n Structure prior P(G) n n n Uniform prior: P(G) constant Prior penalizing number of edges: P(G) c|G| (0<c<1) Normalizing constant across networks is similar and can thus be ignored

Priors Bayesian Score: n Parameter prior P( |G) n BDe prior n n M 0: equivalent sample size B 0: network representing the prior probability of events Set (xi, pai. G) = M 0 P(xi, pai. G| B 0) G are not the same as parents of X in B n Note: pai i 0 G n Compute P(xi, pai | B 0) using standard inference in B 0 BDe has the desirable property that I-equivalent networks have the same Bayesian score when using the BDe prior for some M’ and P’

Bayesian Score: Asymptotic Behavior n For M , a network G with Dirichlet priors satisfies Dim(G): number of independent parameters in G n Approximation is called BIC score n n Score exhibits tradeoff between fit to data and complexity Mutual information grows linearly with M while complexity grows logarithmically with M n As M grows, more emphasis is given to the fit to the data

Bayesian Score: Asymptotic Behavior n For M , a network G with Dirichlet priors satisfies n Bayesian score is consistent n As M , the true structure G* maximizes the score n n Spurious edges will not contribute to likelihood and will be penalized Required edges will be added due to linear growth of likelihood term relative to M compared to logarithmic growth of model complexity

Summary: Network Scores n Likelihood, MDL, (log) BDe have the form n BDe requires assessing prior network n n n Can naturally incorporate prior knowledge BDe is consistent and asymptotically equivalent (up to a constant) to BIC/MDL All are score-equivalent n G I-equivalent to G’ Score(G) = Score(G’)

Optimization Problem Input: n n n Training data Scoring function (including priors, if needed) Set of possible structures n Including prior knowledge about structure Output: n A network (or networks) that maximize the score Key Property: n Decomposability: the score of a network is a sum of terms.

Learning Trees n n At most one parent per variable Why trees? n Elegant math we can solve the optimization problem efficiently (with a greedy algorithm) n Sparse parameterization avoid overfitting while adapting to the data

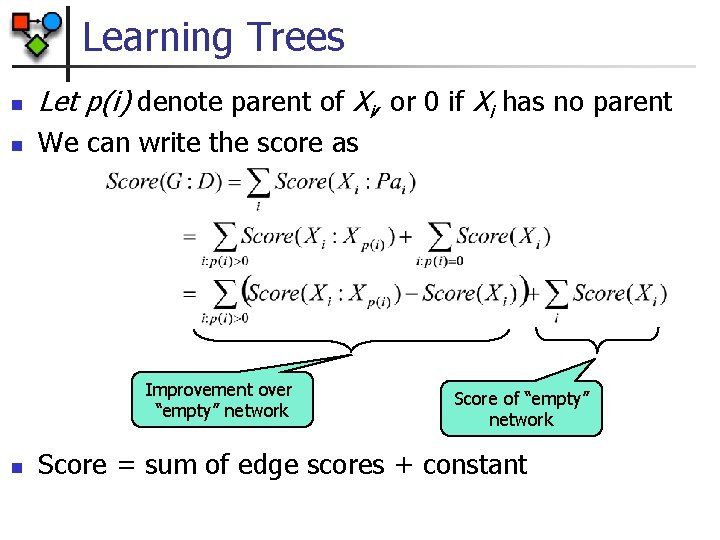
Learning Trees n Let p(i) denote parent of Xi, or 0 if Xi has no parent n We can write the score as Improvement over “empty” network n Score of “empty” network Score = sum of edge scores + constant

Learning Trees n Algorithm n n n Construct graph with vertices: 1, . . . n Set w(i j) = Score(Xj | Xi ) - Score(Xj) Find tree (or forest) with maximal weight n n n This can be done using standard algorithms in low-order polynomial time by building a tree in a greedy fashion (Kruskal’s maximum spanning tree algorithm) Theorem: Procedure finds the tree with maximal score When score is likelihood, then w(i j) is proportional to I(Xi; Xj). This is known as the Chow & Liu method

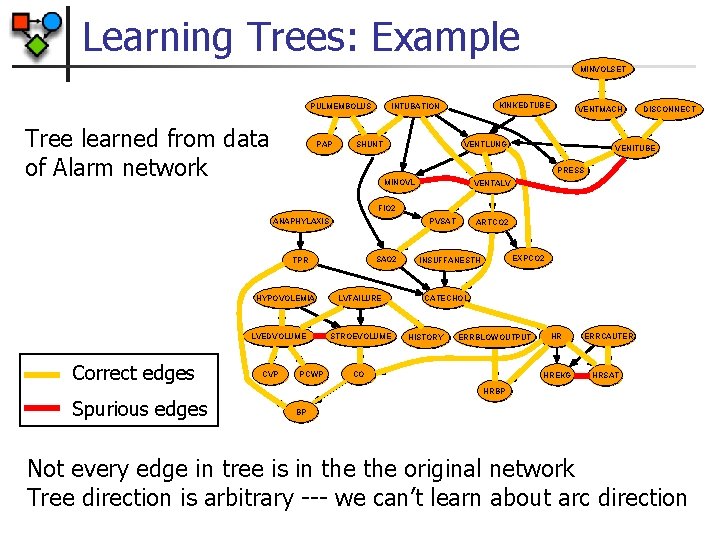
Learning Trees: Example MINVOLSET PULMEMBOLUS Tree learned from data of Alarm network PAP KINKEDTUBE INTUBATION SHUNT VENTMACH VENTLUNG DISCONNECT VENITUBE PRESS MINOVL VENTALV FIO 2 PVSAT ANAPHYLAXIS SAO 2 TPR HYPOVOLEMIA LVEDVOLUME Correct edges CVP PCWP LVFAILURE STROEVOLUME ARTCO 2 EXPCO 2 INSUFFANESTH CATECHOL HISTORY ERRBLOWOUTPUT CO HR HREKG ERRCAUTER HRSAT HRBP Spurious edges BP Not every edge in tree is in the original network Tree direction is arbitrary --- we can’t learn about arc direction

Beyond Trees n Problem is not easy for more complex networks n n n Example: Allowing two parents, greedy algorithm is no longer guaranteed to find the optimal network In fact, no efficient algorithm exists Theorem: n Finding maximal scoring network structure with at most k parents for each variable is NP-hard for k>1

Fixed Ordering n For any decomposable scoring function Score(G: D) and ordering the maximal scoring network has: (since choice at Xi does not constrain other choices) n n For fixed ordering we have independent problems If we bound the in-degree per variable by d, then complexity is exponential in d

Heuristic Search We address the problem by using heuristic search n Define a search space: n n nodes are possible structures edges denote adjacency of structures n Traverse this space looking for high-scoring structures n Search techniques: n n Greedy hill-climbing Best first search Simulated Annealing. . .

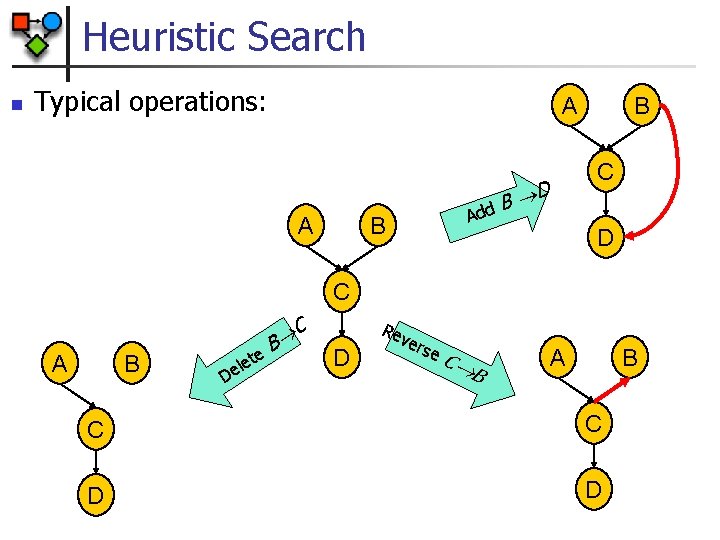
Heuristic Search n Typical operations: A A dd B D A B B C D C A B D te e l e B C D Re ve rse C B A B C C D D

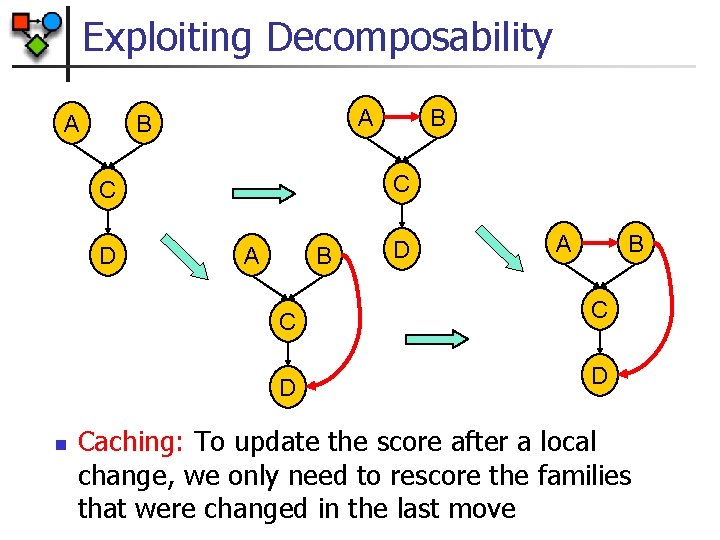
Exploiting Decomposability A A B C C D n B A B D A B C C D D Caching: To update the score after a local change, we only need to rescore the families that were changed in the last move

Greedy Hill Climbing n Simplest heuristic local search n Start with a given network n n At each iteration n n empty network best tree a random network Evaluate all possible changes Apply change that leads to best improvement in score Reiterate Stop when no modification improves score Each step requires evaluating O(n) new changes

Greedy Hill Climbing Pitfalls n Greedy Hill-Climbing can get stuck in: n Local Maxima n n Plateaus n n All one-edge changes reduce the score Some one-edge changes leave the score unchanged Happens because equivalent networks received the same score and are neighbors in the search space Both occur during structure search Standard heuristics can escape both n n Random restarts TABU search

Equivalence Class Search n Idea n n n Search the space of equivalence classes Equivalence classes can be represented by PDAGs (partially ordered graph) Advantages n n PDAGs space has fewer local maxima and plateaus There are fewer PDAGs than DAGs

Equivalence Class Search n Evaluating changes is more expensive n In addition to search, need to score a consistent network X Y Original PDAG Z New PDAG Add Y—Z Consistent DAG X Y Z Score n These algorithms are more complex to implement

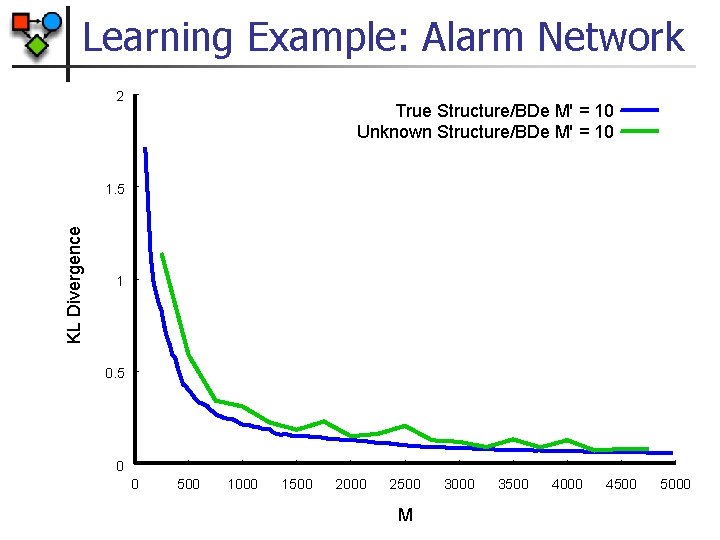
Learning Example: Alarm Network 2 True Structure/BDe M' = 10 Unknown Structure/BDe M' = 10 KL Divergence 1. 5 1 0. 5 0 0 500 1000 1500 2000 2500 M 3000 3500 4000 4500 5000

Model Selection n So far, we focused on single model n n n Find best scoring model Use it to predict next example Implicit assumption: n Best scoring model dominates the weighted sum n n Pros: n n n Valid with many data instances We get a single structure Allows for efficient use in our tasks Cons: n n We are committing to the independencies of a particular structure Other structures might be as probable given the data

Model Selection n Density estimation n n One structure may suffice, if its joint distribution is similar to other high scoring structures Structure discovery n n Define features f(G) (e. g. , edge, sub-structure, d-sep query) Compute n Still requires summing over exponentially many structures

Model Averaging Given an Order n Assumptions n n n Known total order of variables Maximum in-degree for variables d Marginal likelihood Cost per family: O(nd) Total cost: O(nd+1) Using decomposability assumption on prior P(G| ) Since given ordering , parent choices are independent

Model Averaging Given an Order n Posterior probability of a general feature n Posterior probability of particular choice of parents All terms cancel out n Posterior probability of particular edge choice

Model Averaging n We cannot assume that order is known n Solution: Sample from posterior distribution of P(G|D) n n n Estimate feature probability by Sampling can be done by MCMC Sampling can be done over orderings

Notes on Learning Local Structures n Define score with local structures n n Prior may need to be extended n n Example: in tree CPDs, score decomposes by leaves Example: in tree CPDs, penalty for tree structure per CPD Extend search operators to local structure n n Example: in tree CPDs, we need to search for tree structure Can be done by local encapsulated search or by defining new global operations

Search: Summary n n Discrete optimization problem In general, NP-Hard n n Need to resort to heuristic search In practice, search is relatively fast (~100 vars in ~10 min): n n n Decomposability Sufficient statistics In some cases, we can reduce the search problem to an easy optimization problem n Example: learning trees