Hidden Markov Models Conditional Random Fields Eran Segal

Hidden Markov Models & Conditional Random Fields Eran Segal Weizmann Institute

Representing Time n n Add the time dimension to variables X X(t) Assumptions n Time can be discretized into interesting points t 1, t 2, . . . tn n Markov assumption holds n Distribution is stationary (time invariant or homogeneous)

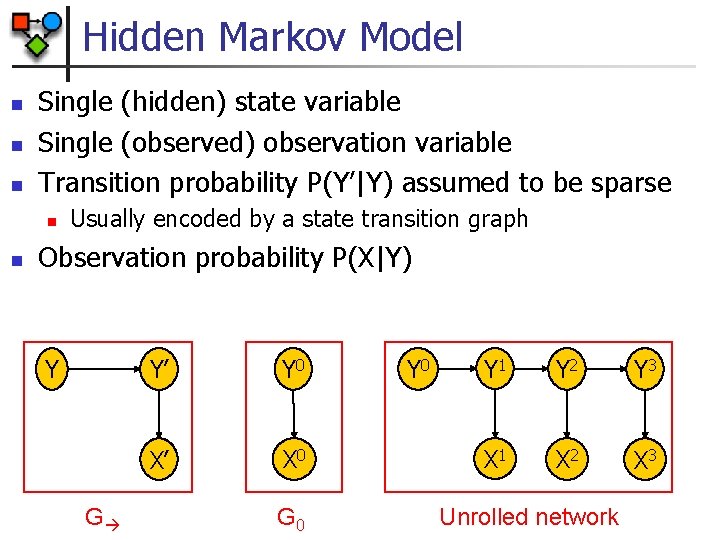
Hidden Markov Model n n n Single (hidden) state variable Single (observed) observation variable Transition probability P(Y’|Y) assumed to be sparse n n Usually encoded by a state transition graph Observation probability P(X|Y) Y G Y’ Y 0 X’ X 0 G 0 Y 1 Y 2 Y 3 X 1 X 2 X 3 Unrolled network

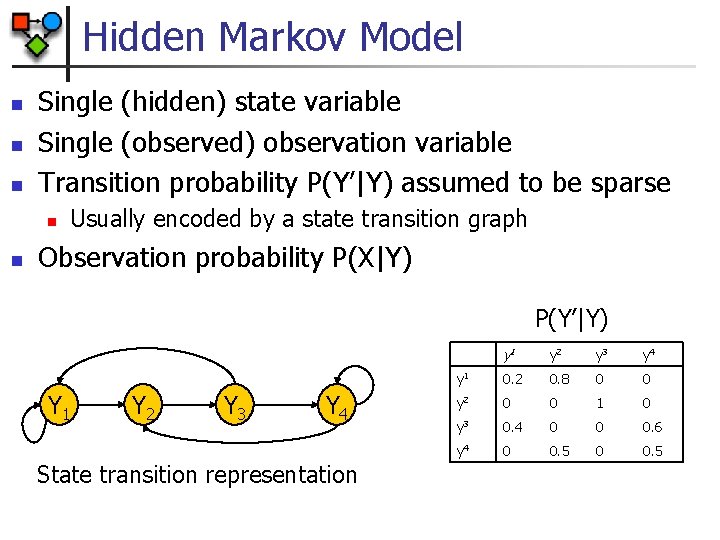
Hidden Markov Model n n n Single (hidden) state variable Single (observed) observation variable Transition probability P(Y’|Y) assumed to be sparse n n Usually encoded by a state transition graph Observation probability P(X|Y) P(Y’|Y) Y 1 Y 2 Y 3 Y 4 State transition representation y 1 y 2 y 3 y 4 y 1 0. 2 0. 8 0 0 y 2 0 0 1 0 y 3 0. 4 0 0 0. 6 y 4 0 0. 5

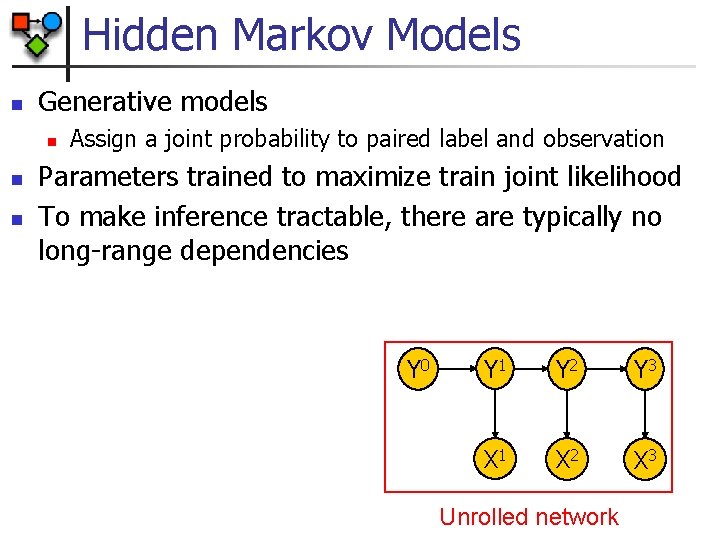
Hidden Markov Models n Generative models n n n Assign a joint probability to paired label and observation Parameters trained to maximize train joint likelihood To make inference tractable, there are typically no long-range dependencies Y 0 Y 1 Y 2 Y 3 X 1 X 2 X 3 Unrolled network

Conditional Models n n n Specifies the probability of possible label sequences given the observations, P(Y|X) Does not “waste” parameters on modeling P(X|Y) Key advantage: n n n Distribution over Y can depend on non-independent features without modeling feature dependencies Transition probabilities can depend on past and future Two representations n n Maximum Entropy Markov Models (MEMMs) Conditional Random Fields (CRFs)

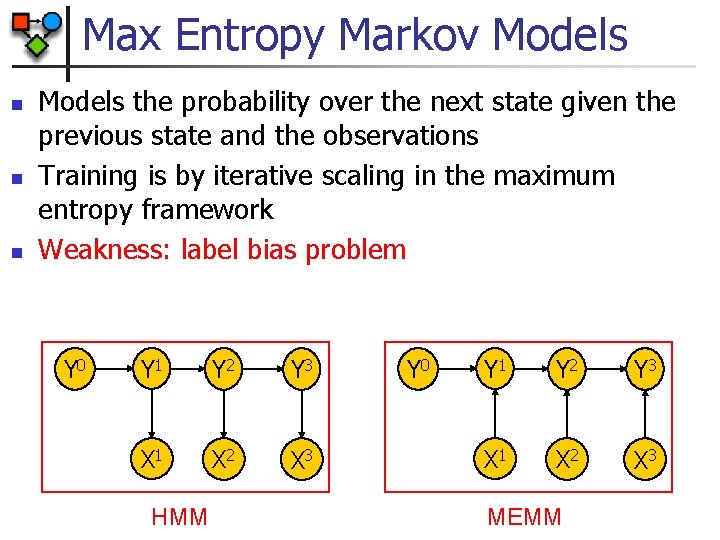
Max Entropy Markov Models n n n Models the probability over the next state given the previous state and the observations Training is by iterative scaling in the maximum entropy framework Weakness: label bias problem Y 0 Y 1 Y 2 Y 3 X 1 X 2 X 3 HMM Y 0 Y 1 Y 2 Y 3 X 1 X 2 X 3 MEMM

Label-Bias Problem of MEMMs n Transitions from a state compete only with each other n n Transition scores are conditional probabilities of next states given current state and observation This implies a “conservation of score mass” whereby mass of a state is distributed among next states Observations do not affect the total mass of next states Biases for states with fewer outgoing transitions n n States with a single outgoing transition ignore observations Unlike HMMs, observations after a branch point in a path are ignored

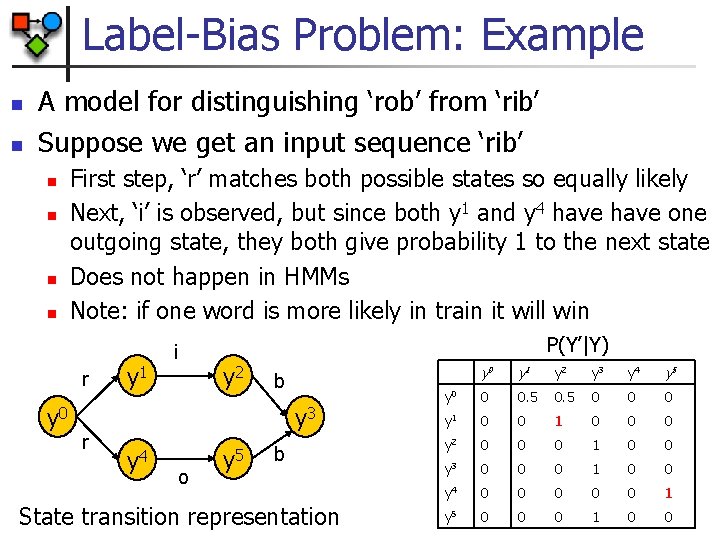
Label-Bias Problem: Example n n A model for distinguishing ‘rob’ from ‘rib’ Suppose we get an input sequence ‘rib’ n n First step, ‘r’ matches both possible states so equally likely Next, ‘i’ is observed, but since both y 1 and y 4 have one outgoing state, they both give probability 1 to the next state Does not happen in HMMs Note: if one word is more likely in train it will win r y 1 i P(Y’|Y) y 2 b y 0 y 3 r y 4 o y 5 b State transition representation y 0 y 1 y 2 y 3 y 4 y 5 y 0 0 0. 5 0 0 0 y 1 0 0 0 y 2 0 0 0 1 0 0 y 3 0 0 0 1 0 0 y 4 0 0 0 1 y 5 0 0 0 1 0 0

Conditional Random Fields n n Advantages of MEMMs without the label bias problem Key difference n n MEMMs use per-state model for conditional probabilities of next state given current state CRFs have a single model for the joint probability of the entire sequence of labels given the observations n n Thus, weights of different features at different states can trade off against each other CRF training n n Maximum likelihood or MAP Loss function is convex, guaranteeing convergence to global optimum

Conditional Random Fields n n Let G=(V, E) be a graph with vertices V and edges E, such that Then (X, Y) is a CRF if the random variables Yv obey the Markov property with respect to the graph: n n where Yj is the set of Y neighbors of Yi Model only P(Y|X) Y 0 Y 1 Y 2 Y 3 X 1 X 2 X 3 CRF

Conditional Random Fields n Joint probability distribution for trees over Y n n n n Cliques (and thus potentials) are the edges and vertices x are the observed variables y are the state variables y[S] is the components of Y associated with vertices in S fk is an edge feature with weight λk gk is a vertex feature with weight μk Note that features can be over all of variables in x

Representing HMMs with CRFs n An HMM can be represented by the following CRF n n where Note that we defined one feature for each state pair (y’, y) and one feature for each state-observation pair (y, x)

Parameter Estimation

Applications

Conditional Random Fields n Joint probability distribution for trees over Y n Cliques (and thus potentials) are the edges and vertices