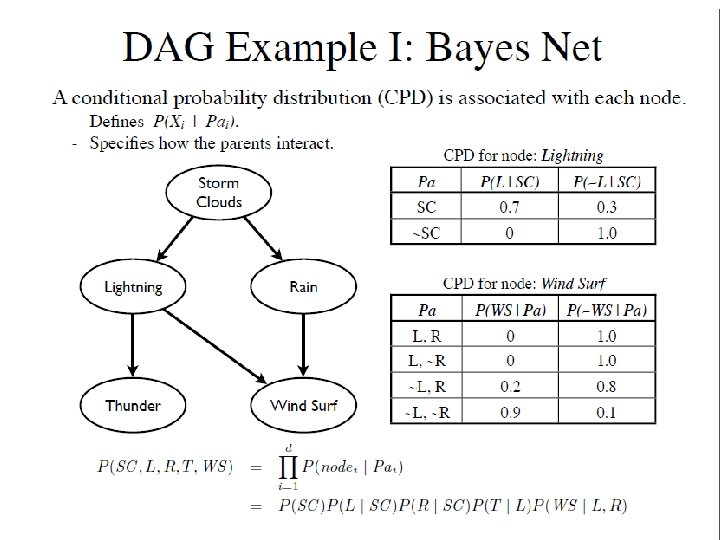
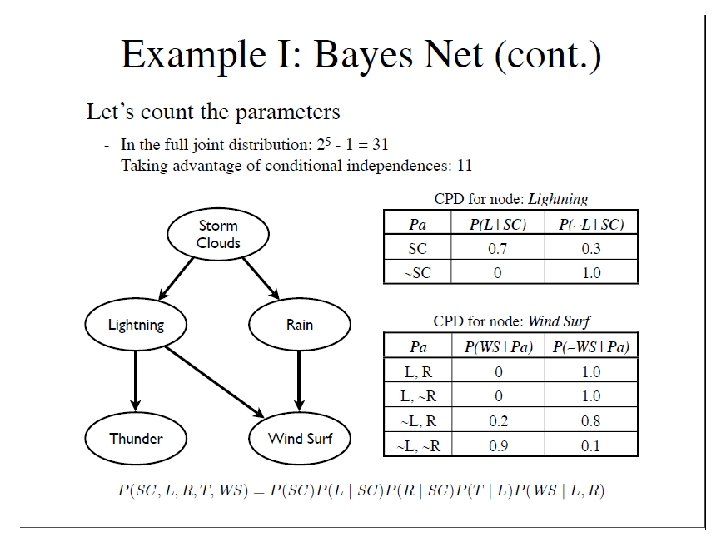
Bayesian Networks II What Bayesian Networks are good

Bayesian Networks II
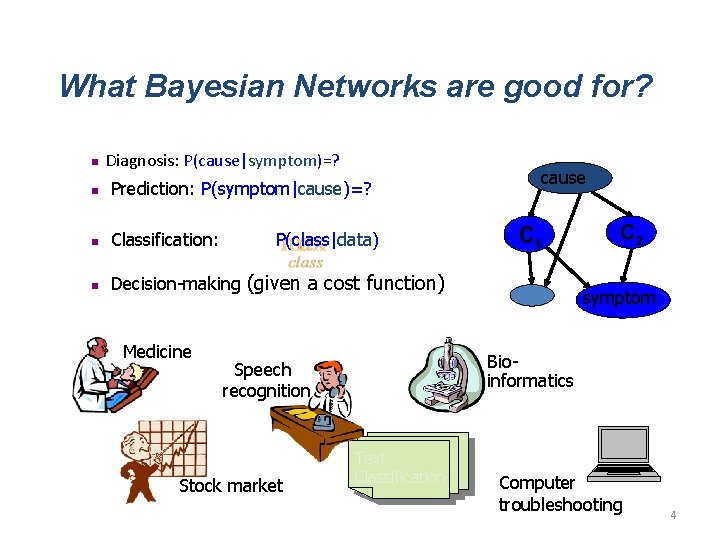
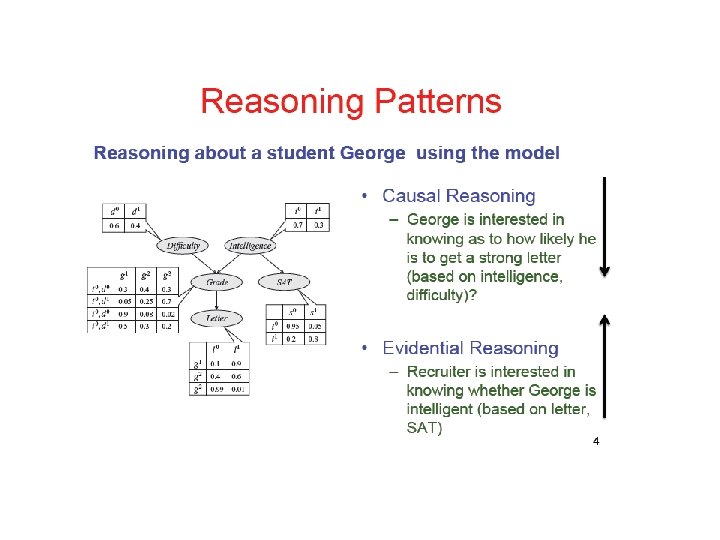
What Bayesian Networks are good for? n Diagnosis: P(cause|symptom)=? n Prediction: P(symptom|cause)=? n Classification: n Decision-making (given a cost function) Medicine cause P(class|data) Bioinformatics Speech recognition Stock market symptom Text Classification Computer troubleshooting 4
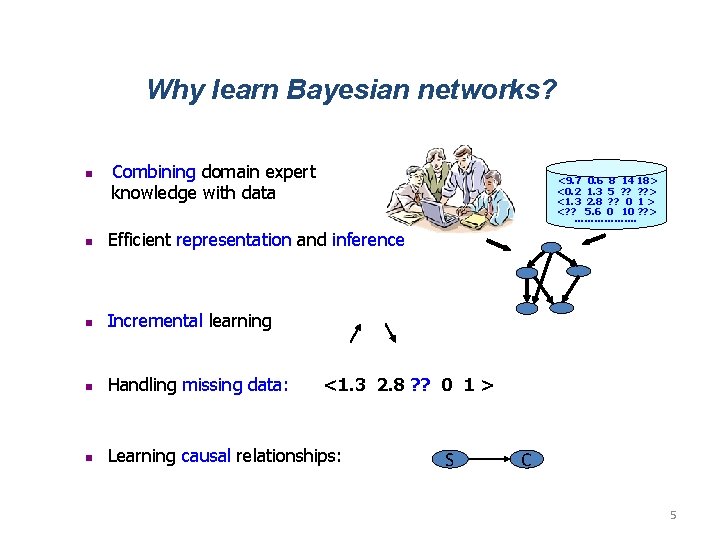
Why learn Bayesian networks? n Combining domain expert knowledge with data <9. 7 0. 6 8 14 18> <0. 2 1. 3 5 ? ? > <1. 3 2. 8 ? ? 0 1 > <? ? 5. 6 0 10 ? ? > ………………. n Efficient representation and inference n Incremental learning n Handling missing data: n Learning causal relationships: <1. 3 2. 8 ? ? 0 1 > S C 5
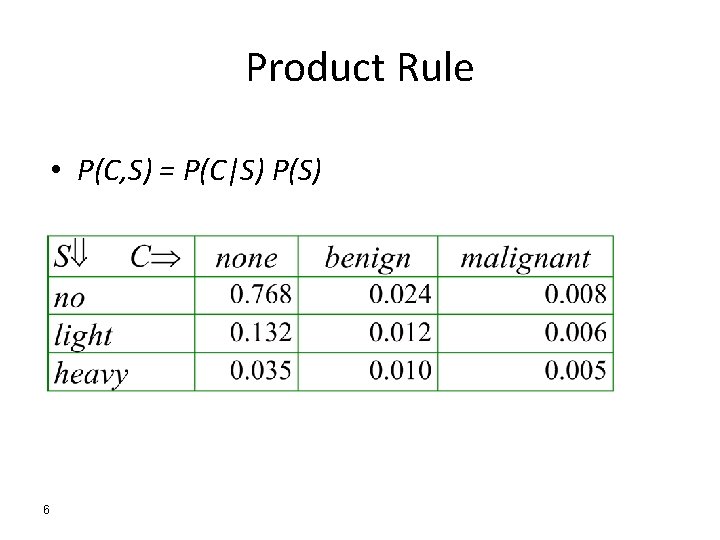
Product Rule • P(C, S) = P(C|S) P(S) 6

Marginalization P(Smoke) P(Cancer) 7
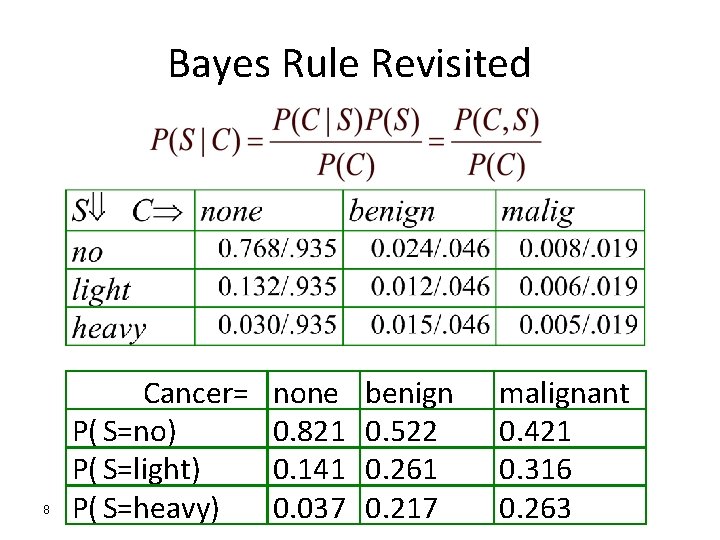
Bayes Rule Revisited 8 Cancer= P( S=no) P( S=light) P( S=heavy) none 0. 821 0. 141 0. 037 benign 0. 522 0. 261 0. 217 malignant 0. 421 0. 316 0. 263
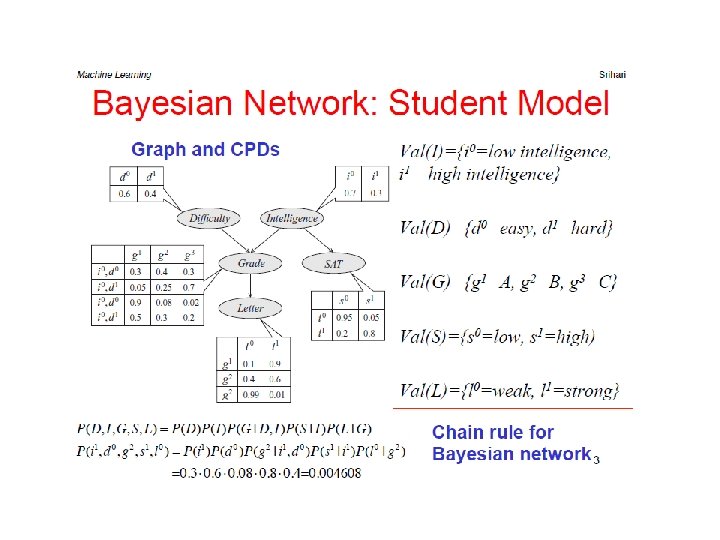
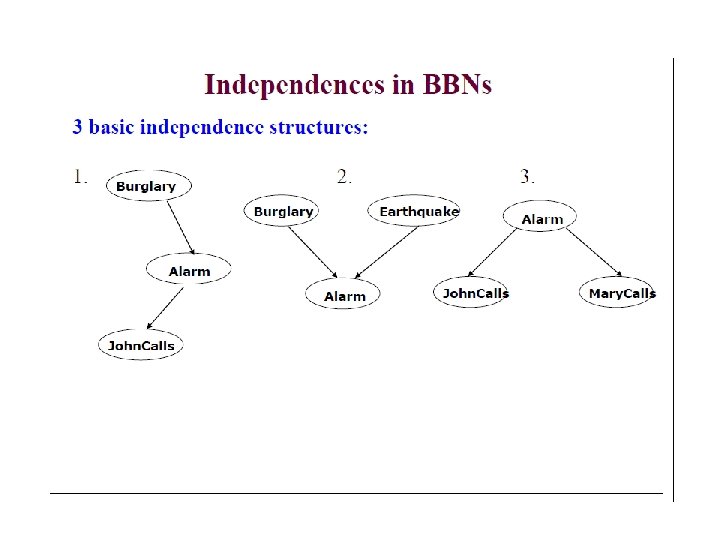
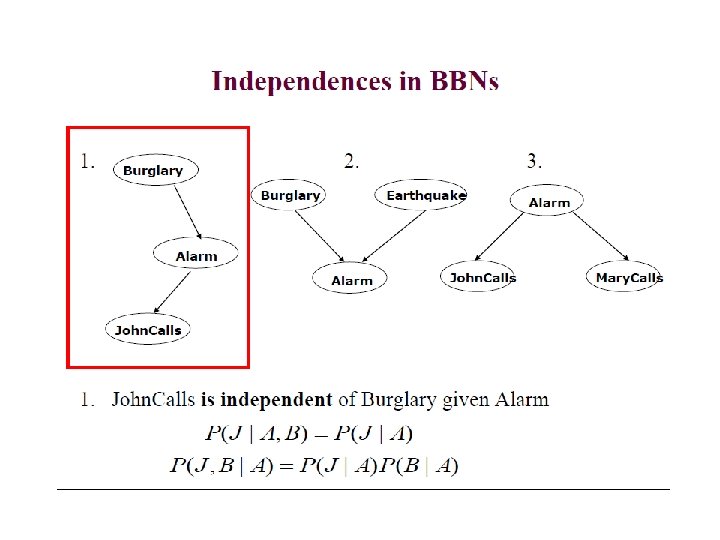
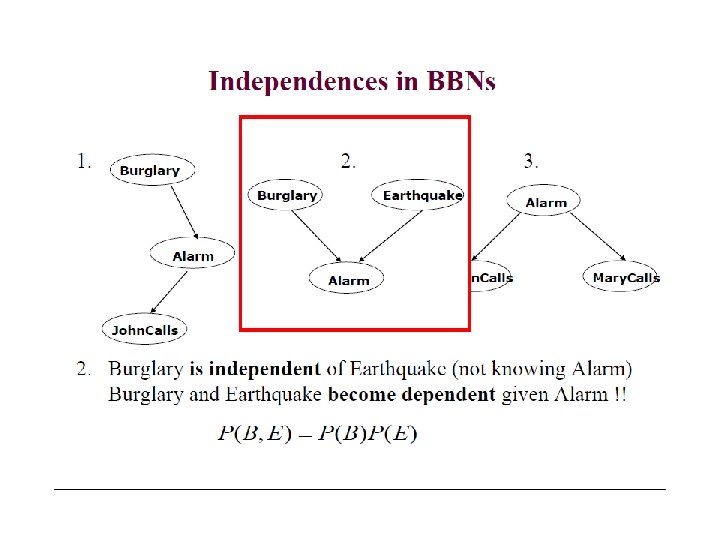
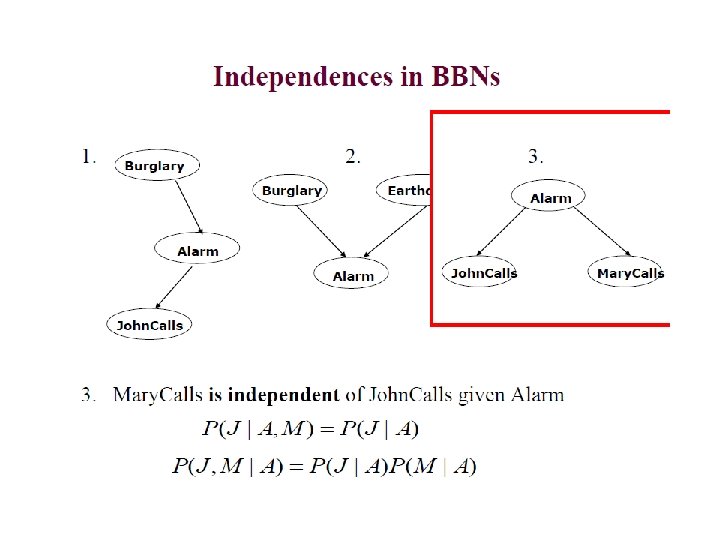
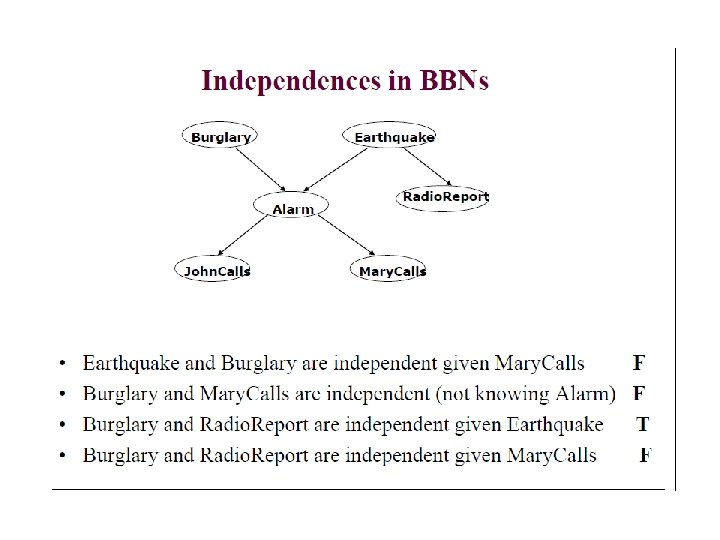

Kinds of inference


Causes Causal inference: P(W|C) = P(W|R, S) P(R, S|C) + P(W|~R, S) P(~R, S|C) + P(W|R, ~S) P(R, ~S|C) + P(W|~R, ~S) P(~R, ~S|C) and use the fact that P(R, S|C) = P(R|C) P(S|C) Diagnostic: P(C|W ) = ? Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 18

Causes and Bayes’ Rule diagnostic causal Diagnostic inference: Knowing that the grass is wet, what is the probability that rain is the cause? Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 19

Causal vs Diagnostic Inference Causal inference: If the sprinkler is on, what is the probability that the grass is wet? P(W|S) = P(W|R, S) P(R|S) + P(W|~R, S) P(~R|S) = P(W|R, S) P(R) + P(W|~R, S) P(~R) = 0. 95 0. 4 + 0. 9 0. 6 = 0. 92 Diagnostic inference: If the grass is wet, what is the probability that the sprinkler is on? P(S|W) = 0. 35 > 0. 2 P(S) P(S|R, W) = 0. 21 Explaining away: Knowing that it has rained decreases the probability that the sprinkler is on. Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 20
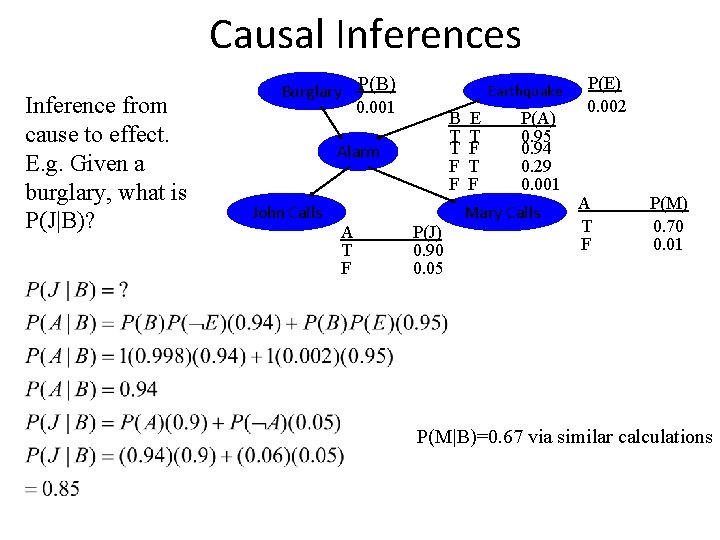
Causal Inferences Inference from cause to effect. E. g. Given a burglary, what is P(J|B)? Burglary P(B) 0. 001 Earthquake B T T F F Alarm John Calls A T F P(J) 0. 90 0. 05 E T F P(A) 0. 95 0. 94 0. 29 0. 001 Mary Calls P(E) 0. 002 A T F P(M) 0. 70 0. 01 P(M|B)=0. 67 via similar calculations


Diagnostic Inferences From effect to cause. E. g. Given that John calls, what is the P(burglary)? What is P(J)? Need P(A) first: Many false positives.
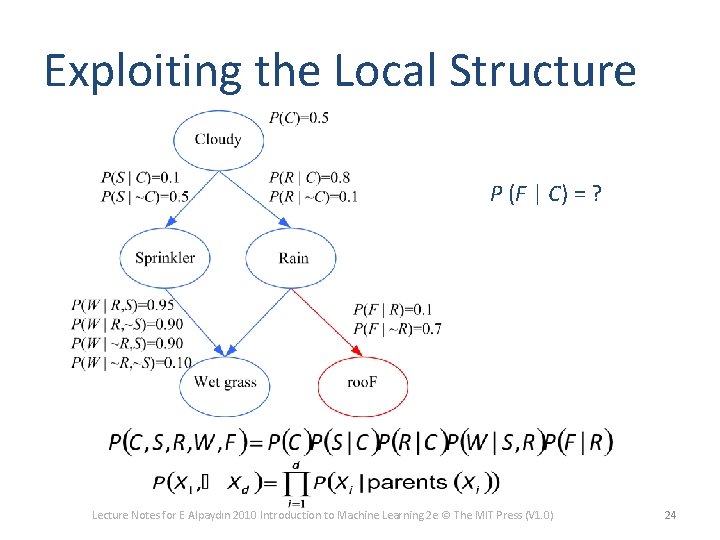
Exploiting the Local Structure P (F | C) = ? Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 24
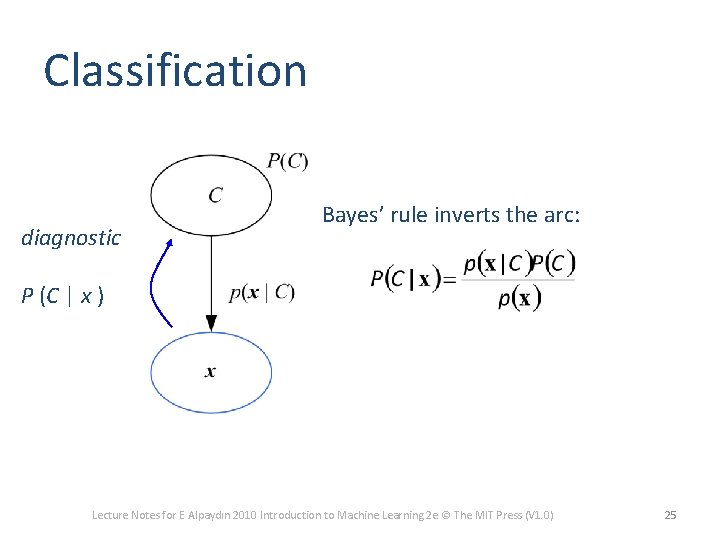
Classification diagnostic Bayes’ rule inverts the arc: P (C | x ) Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 25

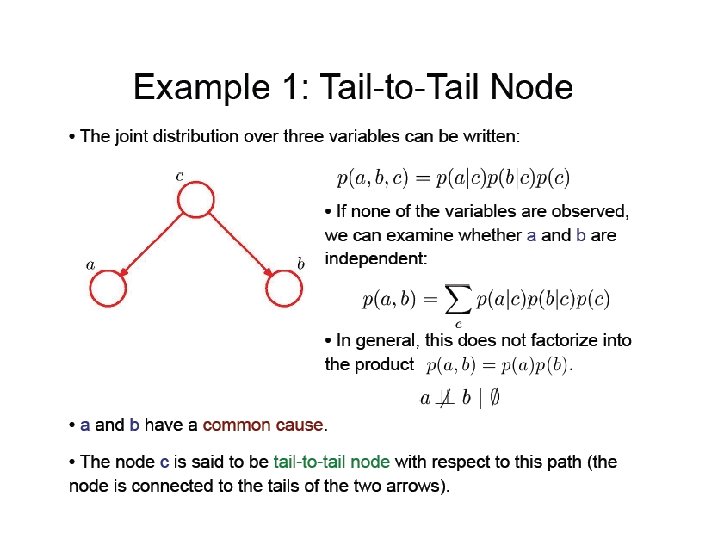
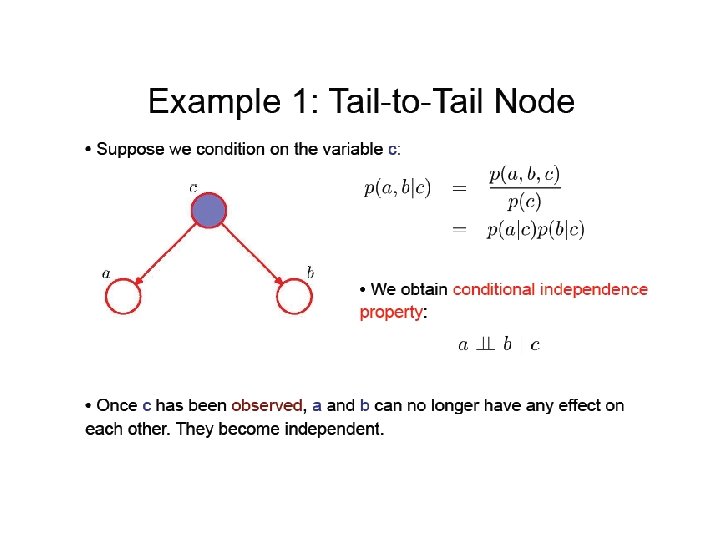
Conditional Independence • X and Y are independent if P(X, Y)=P(X)P(Y) • X and Y are conditionally independent given Z if P(X, Y|Z)=P(X|Z)P(Y|Z) or P(X|Y, Z)=P(X|Z) • Three canonical cases: Head-to-tail, Tail-to-tail, head-to-head Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 26










Case 1: Head-to-Head • P(X, Y, Z)=P(X)P(Y|X)P(Z|Y) • P(W|C)=P(W|R)P(R|C)+P(W|~R)P(~R|C) Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 36

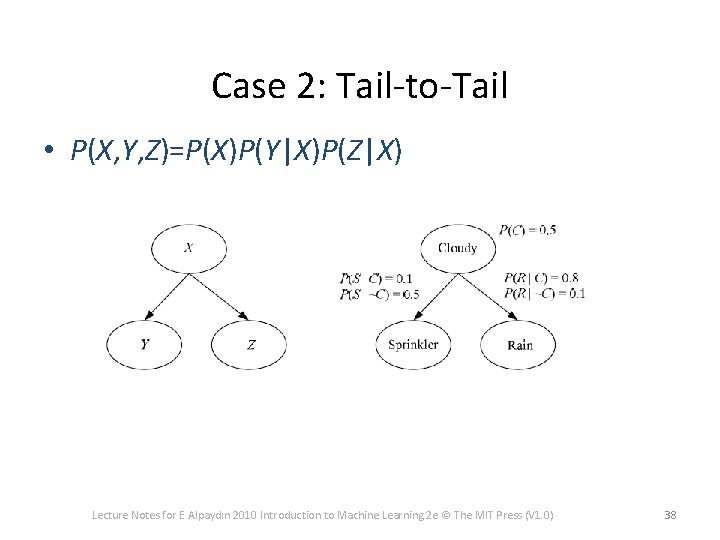
Case 2: Tail-to-Tail • P(X, Y, Z)=P(X)P(Y|X)P(Z|X) Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 38

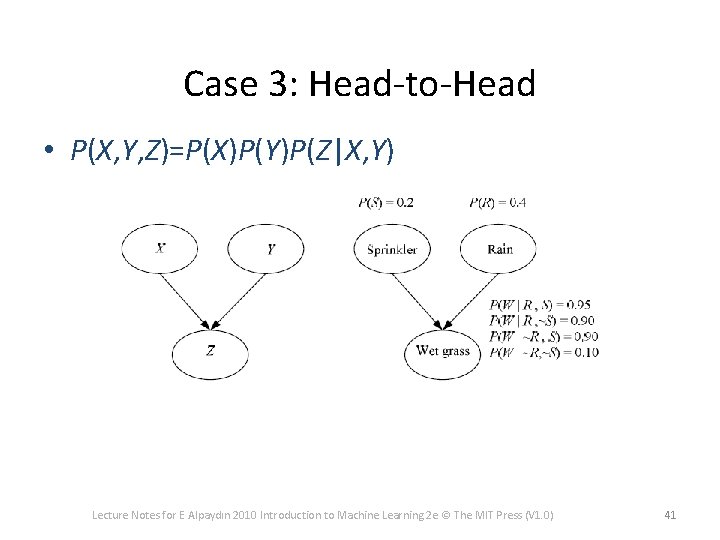
Case 3: Head-to-Head • P(X, Y, Z)=P(X)P(Y)P(Z|X, Y) Lecture Notes for E Alpaydın 2010 Introduction to Machine Learning 2 e © The MIT Press (V 1. 0) 41


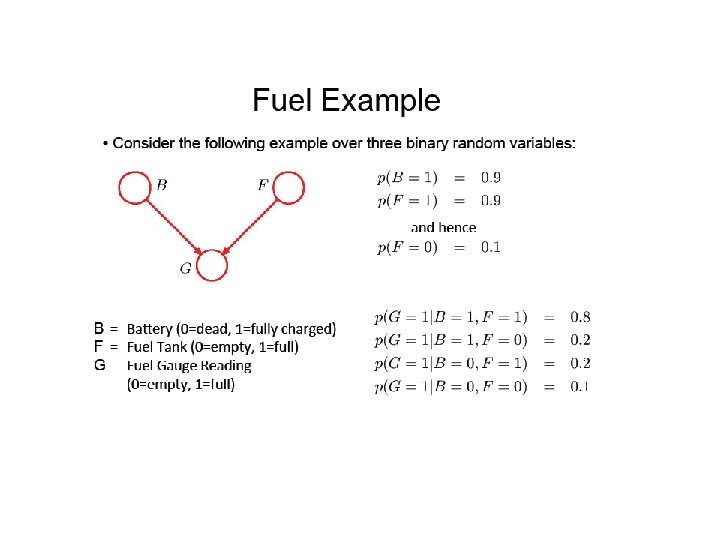


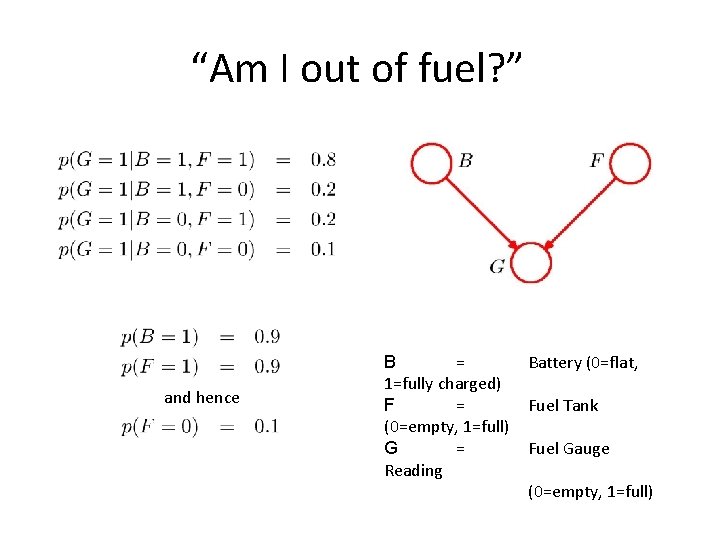
“Am I out of fuel? ” and hence B = 1=fully charged) F = (0=empty, 1=full) G = Reading Battery (0=flat, Fuel Tank Fuel Gauge (0=empty, 1=full)
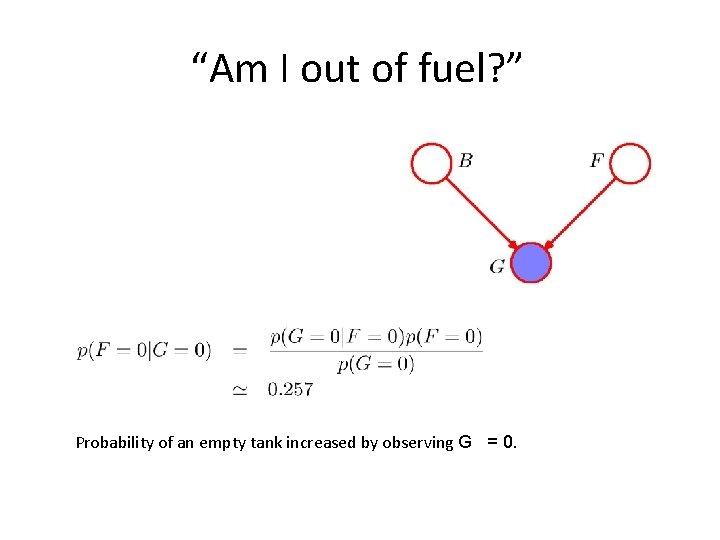
“Am I out of fuel? ” Probability of an empty tank increased by observing G = 0.
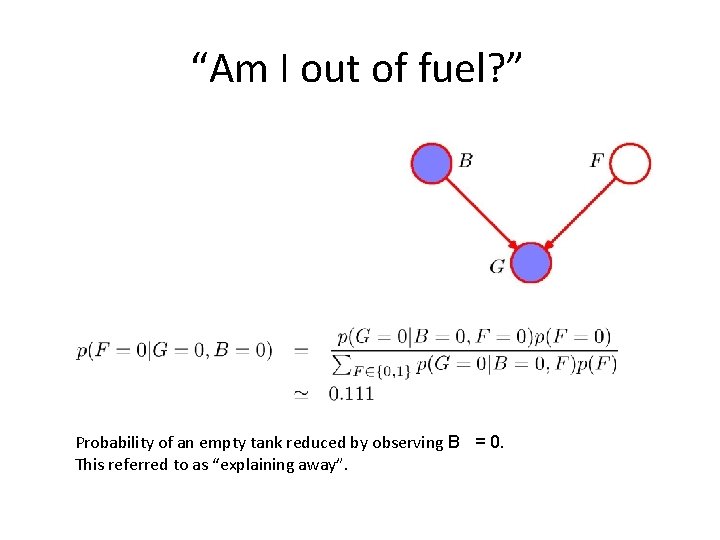
“Am I out of fuel? ” Probability of an empty tank reduced by observing B = 0. This referred to as “explaining away”.



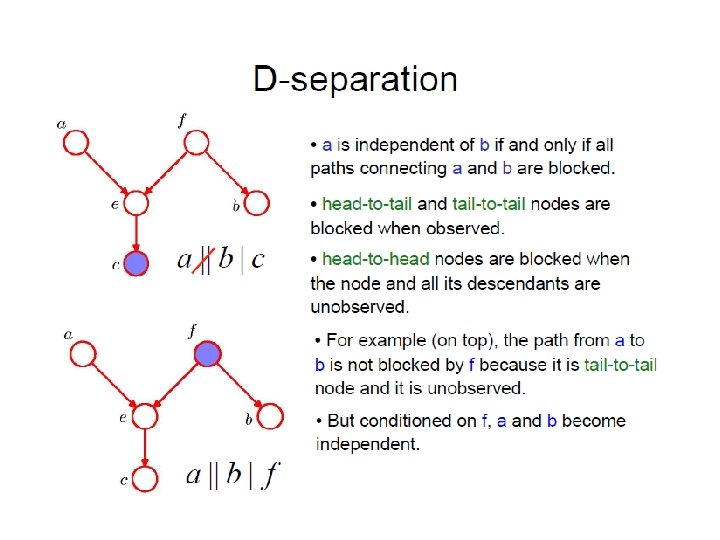
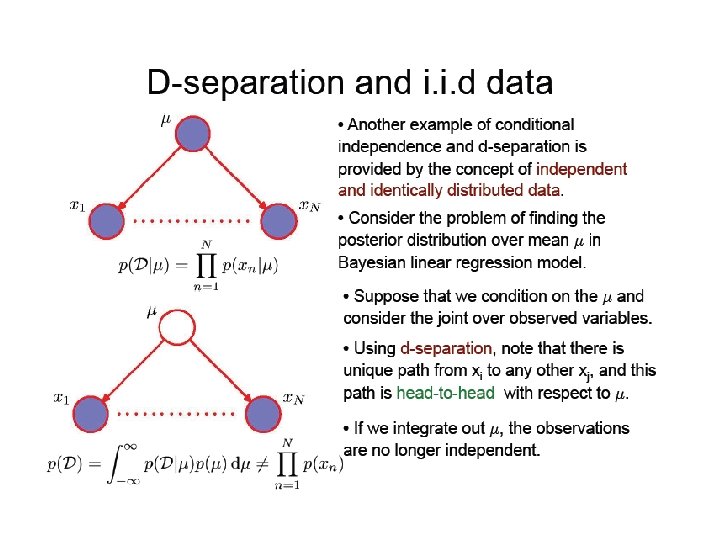
D-separation • A, B, and C are non-intersecting subsets of nodes in a directed graph. • A path from A to B is blocked if it contains a node such that either a) the arrows on the path meet either head-to-tail or tailto-tail at the node, and the node is in the set C, or b) the arrows meet head-to-head at the node, and neither the node, nor any of its descendants, are in the set C. • If all paths from A to B are blocked, A is said to be dseparated from B by C. • If A is d-separated from B by C, the joint distribution over all variables in the graph satisfies.



Directed Graphs as Distribution Filters

- Slides: 60