Undirected Graphical Models Eran Segal Weizmann Institute Undirected

Undirected Graphical Models Eran Segal Weizmann Institute

Undirected Graphical Models n n Useful when edge directionality cannot be assigned Simpler interpretation of structure n n n Simpler inference Simpler independency structure Harder to learn We will also see models with combined directed and undirected edges Some computations require restriction to discrete variables

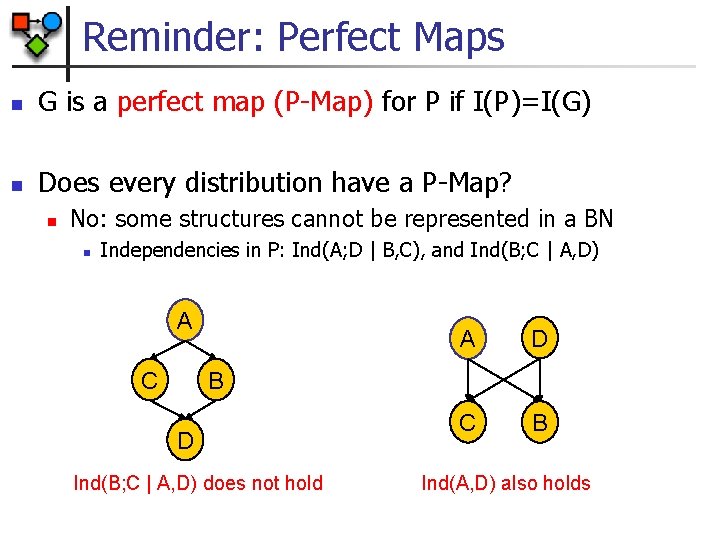
Reminder: Perfect Maps n G is a perfect map (P-Map) for P if I(P)=I(G) n Does every distribution have a P-Map? n No: some structures cannot be represented in a BN n Independencies in P: Ind(A; D | B, C), and Ind(B; C | A, D) A C A D C B B D Ind(B; C | A, D) does not hold Ind(A, D) also holds

Representing Dependencies n Ind(A; D | B, C), and Ind(B; C | A, D) n n Cannot be modeled with a Bayesian network without extraneous edges Can be modeled with an undirected (Markov) network

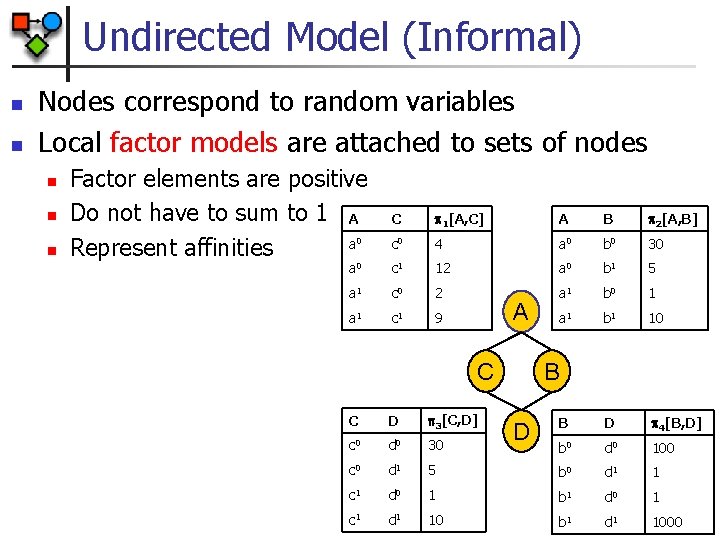
Undirected Model (Informal) n n Nodes correspond to random variables Local factor models are attached to sets of nodes n n n Factor elements are positive Do not have to sum to 1 A a Represent affinities C 1[A, C] A B 2[A, B] 0 c 0 4 a 0 b 0 30 a 0 c 1 12 a 0 b 1 5 a 1 c 0 2 a 1 b 0 1 a 1 c 1 9 a 1 b 1 10 B D 4[B, D] b 0 d 0 100 A C B C D 3[C, D] c 0 d 0 30 c 0 d 1 5 b 0 d 1 1 c 1 d 0 1 b 1 d 0 1 c 1 d 1 10 b 1 d 1 1000 D

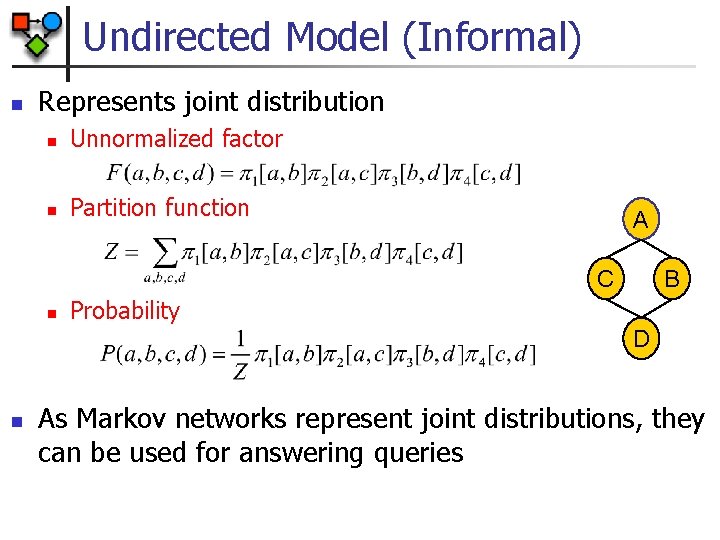
Undirected Model (Informal) n Represents joint distribution n Unnormalized factor n Partition function A C n B Probability D n As Markov networks represent joint distributions, they can be used for answering queries

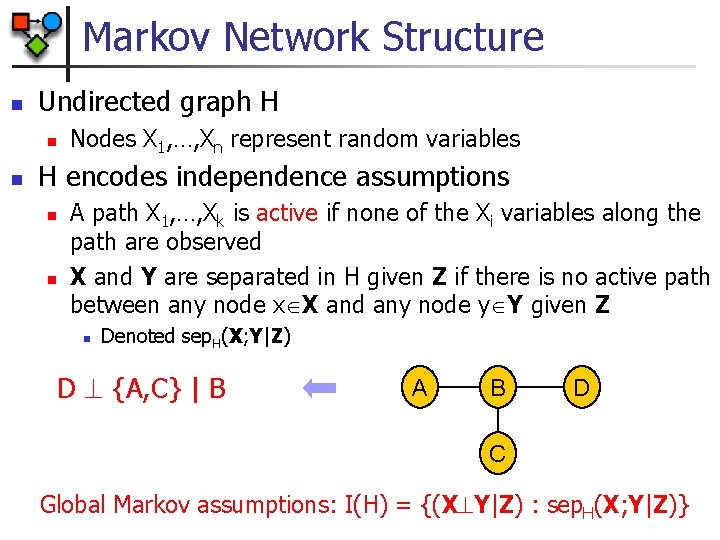
Markov Network Structure n Undirected graph H n n Nodes X 1, …, Xn represent random variables H encodes independence assumptions n n A path X 1, …, Xk is active if none of the Xi variables along the path are observed X and Y are separated in H given Z if there is no active path between any node x X and any node y Y given Z n Denoted sep. H(X; Y|Z) D {A, C} | B A B D C Global Markov assumptions: I(H) = {(X Y|Z) : sep. H(X; Y|Z)}

Relationship with Bayesian Network n Can all independencies encoded by Markov networks be encoded by Bayesian networks? n n Can all independencies encoded by Bayesian networks be encoded by Markov networks? n n No, Ind(A; B | C, D) and Ind(C; D | A, B) example No, immoral v-structures (explaining away) Markov networks encode monotonic independencies n If sep. H(X; Y|Z) and Z Z’ then sep. H(X; Y|Z’)

Markov Network Factors n A factor is a function from value assignments of a set of random variables D to real positive numbers + n n The set of variables D is the scope of the factor Factors generalize the notion of CPDs n Every CPD is a factor (with additional constraints)

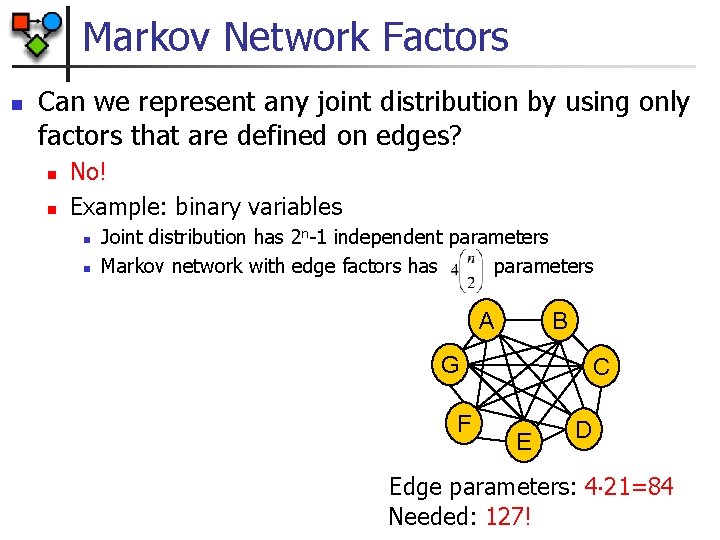
Markov Network Factors n Can we represent any joint distribution by using only factors that are defined on edges? n n No! Example: binary variables n n Joint distribution has 2 n-1 independent parameters Markov network with edge factors has parameters A B G F C E D Edge parameters: 4 21=84 Needed: 127!

Markov Network Factors n Are there constraints imposed on the network structure H by a factor whose scope is D? n n Hint 1: think of the independencies that must be satisfied Hint 2: generalize from the basic case of |D|=2 The induced subgraph over D must be a clique (fully connected) (otherwise two unconnected variables may be independent by blocking the active path between them, contradicting the direct dependency between them in the factor over D)

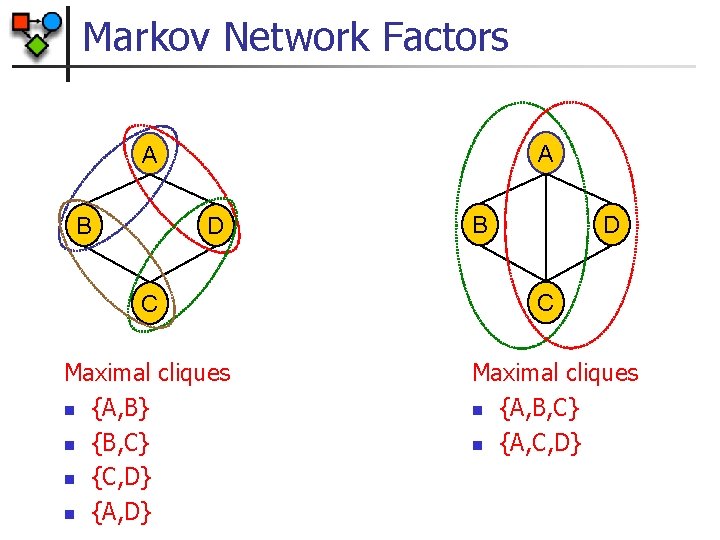
Markov Network Factors A A B D C Maximal cliques n {A, B} n {B, C} n {C, D} n {A, D} B D C Maximal cliques n {A, B, C} n {A, C, D}

Markov Network Distribution n A distribution P factorizes over H if it has: n n A set of subsets D 1, . . . Dm where each Di is a complete subgraph in H Factors 1[D 1], . . . , m[Dm] such that where: n n Z is called the partition function P is also called a Gibbs distribution over H

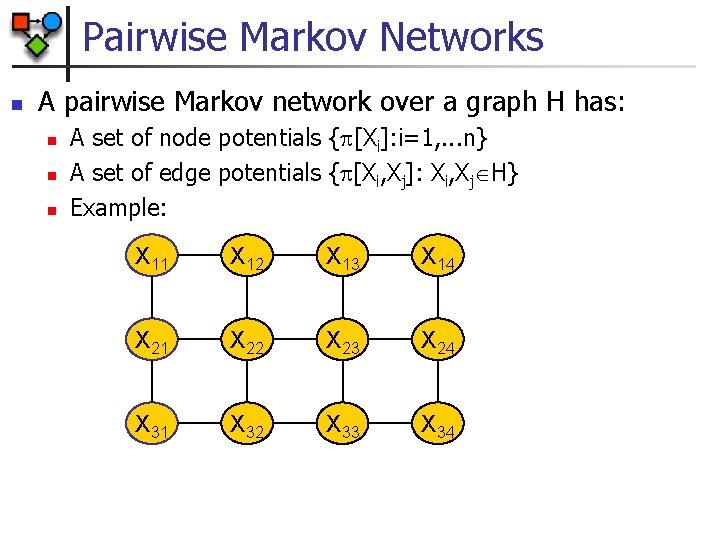
Pairwise Markov Networks n A pairwise Markov network over a graph H has: n n n A set of node potentials { [Xi]: i=1, . . . n} A set of edge potentials { [Xi, Xj]: Xi, Xj H} Example: X 11 X 12 X 13 X 14 X 21 X 22 X 23 X 24 X 31 X 32 X 33 X 34

Logarithmic Representation n We represent energy potentials by applying a log transformation to the original potentials n n [D]=exp(- [D]) where [D]=-ln [D] Any Markov network parameterized with factors can be converted to a logarithmic representation The log-transformed potentials can take on any real value The joint distribution decomposes as

I-Maps and Factorization n I-Map n n An I-Map I(P) is the set of independencies (X Y | Z) in P Bayesian Networks n Factorization and reverse factorization theorems n n G is an I-map of P iff P factorizes as Markov Networks n Factorization and reverse factorization theorems n H is an I-map of P iff P factorizes as

Reverse Factorization H is an I-map of P n n Proof: n n n Let X, Y, W be any three disjoint sets of variables such that W separates X and Y in H We need to show Ind(X; Y|W) P Case 1: X Y W=U (all variables) n As W separates X and Y there are no direct edges between X and Y any clique in H is fully contained in X W or Y W Let IX be subcliques in X W and IY be subcliques in Y W n Ind(X; Y|W) P n n n

Reverse Factorization H is an I-map of P n n Proof: n n n Let X, Y, W be any three disjoint sets of variables such that W separates X and Y in H We need to show Ind(X; Y|W) P Case 2: X Y W U (all variables) n n Let S=U-(X Y W) S can be partitioned into two disjoint sets S 1 and S 2 such that W separates X S 1 and Y S 2 in H From case 1, we can derive Ind(X, S 1; Y, S 2|W) P From decomposition of independencies Ind(X; Y|W) P

Factorization n Holds only for positive distributions P If H is an I-map of P then n Defer proof n

d-Separation: Completeness n Theorem: § d-sep. G(X; Y | Z) = no n Proof outline: n n There exists P such that § G is an I-map of P § P does not satisfy Ind(X; Y | Z) Construct distribution P where independence does not hold Since there is no d-sep, there is an active path For each interaction in the path, correlate the variables through the distribution in the CPDs Set all other CPDs to uniform, ensuring that influence flows only in a single path and cannot be cancelled out

Separation: Completeness n Theorem: § sep. H(X; Y | Z) = no n Proof outline: n n There exists P such that § H is an I-map of P § P does not satisfy Ind(X; Y | Z) Construct distribution P where independence does not hold Since there is no sep, there is an active path For each interaction in the path, correlate the variables through the potentials Set all other potentials to uniform, ensuring that influence flows only in a single path and cannot be cancelled out

Relationship with Bayesian Network n Bayesian Networks n n Semantics defined via local Markov assumptions Global independencies induced by d-separation Local and global independencies equivalent since one implies the other Markov Networks n n Semantics defined via global separation property Can we define the induced local independencies? n n We show two definitions All three definitions (global and two local) are equivalent only for positive distributions P

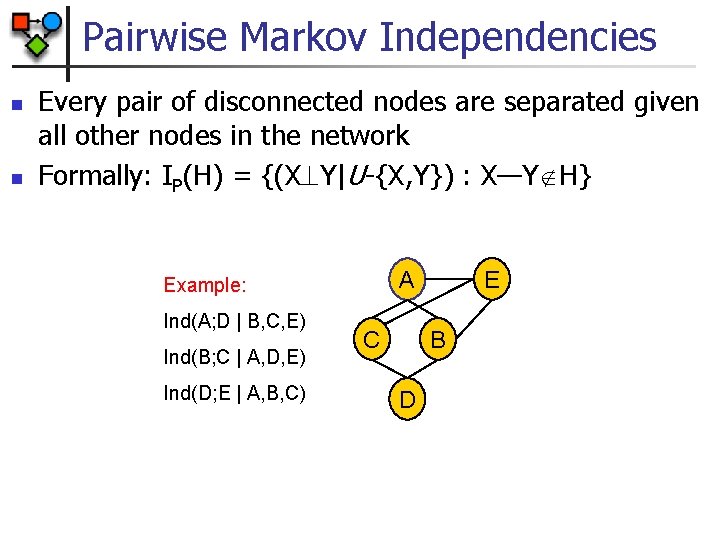
Pairwise Markov Independencies n n Every pair of disconnected nodes are separated given all other nodes in the network Formally: IP(H) = {(X Y|U-{X, Y}) : X—Y H} Ind(A; D | B, C, E) Ind(B; C | A, D, E) Ind(D; E | A, B, C) E A Example: C B D

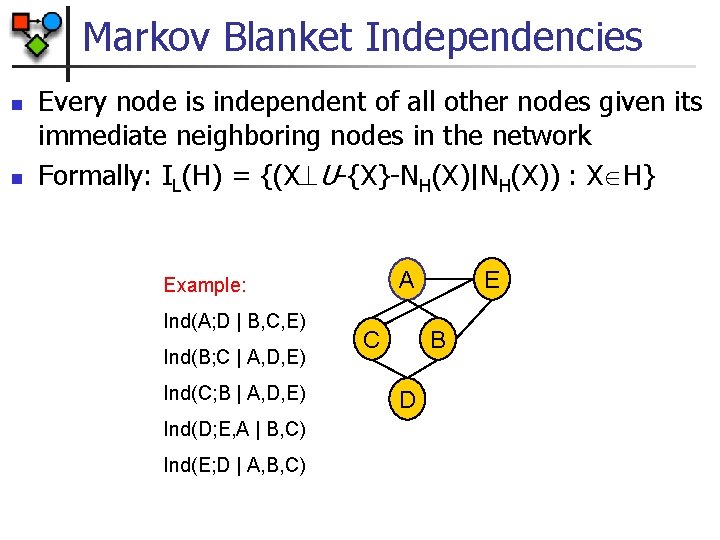
Markov Blanket Independencies n n Every node is independent of all other nodes given its immediate neighboring nodes in the network Formally: IL(H) = {(X U-{X}-NH(X)|NH(X)) : X H} Ind(A; D | B, C, E) Ind(B; C | A, D, E) Ind(C; B | A, D, E) Ind(D; E, A | B, C) Ind(E; D | A, B, C) E A Example: C B D

Relationship Between Properties n Let I(H) be the global separation independencies Let IL(H) be the Markov blanket independencies Let IP(H) be the pairwise Markov independencies n For any distribution P: n n n I(H) IL(H) n n The assertion in IL(H), that a node is independent of all other nodes given its neighbors, is part of the separation independencies since there is no active path between a node and its non-neighbors given its neighbors IL(H) IP(H) n Follows from the monotonicity of independencies in Markov networks (if Ind(X; Y|Z) and Z Z’ then Ind(X; Y|Z’))

Relationship Between Properties n Let I(H) be the global separation independencies Let IL(H) be the Markov blanket independencies Let IP(H) be the pairwise Markov independencies n For any positive distribution P: n n n IP(H) I(H) n n Proof relies on intersection property for probabilities Ind(X; Y|Z, W) and Ind(X; W|Z, Y) Ind(X; Y, W|Z) which holds in general only for positive distributions Thus, for positive distributions n I(H) IL(H) IP(H)

The Need for Positive Distribution n Let P satisfy n n n B C P satisfies IP(H) and IL(H) n n Ind(A; E) A and E uniformly distributed B=A D=E C=B D A E. g. , Ind(B; D, E|A, C) (since A determines B) D P does not satisfy I(H) n E. g. , Ind(A; E|C) does not hold in P but should exist according to separation E

The Need for Positive Distribution n Let P satisfy n n A is uniformly distributed A=B=C A B n P satisfies IP(H) n n Ind(B; C|A), Ind(A; C|B) (since each variable determines all others) C P does not satisfy IL(H) n Ind(C; A, B) needs to hold according to IL(H) but does not hold in the distribution

Constructing Markov Network for P n Goal: Given a distribution, we want to construct a Markov network which is an I-map of P n Complete graphs will satisfy but are not interesting n Minimal I-maps: A graph G is a minimal I-Map for P if: n n n G is an I-map for P Removing any edge from G renders it not an I-map Goal: construct a graph which is a minimal I-map of P

Constructing Markov Network for P n If P is a positive distribution then I(H) IL(H) IP(H) n n Construction algorithm n n Thus, sufficient to construct a network that satisfies IP(H) For every (X, Y) add edge if Ind(X; Y|U-{X, Y}) does not hold Theorem: network is minimal and unique I-map n Proof: n n n I-map follows since IP(H) by construction and I(H) by equivalence Minimality follows since deleting an edge implies Ind(X; Y| U-{X, Y}) But, we know by construction that this does not hold since we added the edge in the construction process Uniqueness follows since any other I-map has at least these edges and to be minimal cannot have additional edges

Constructing Markov Network for P n If P is a positive distribution then I(H) IL(H) IP(H) n n Construction algorithm n n Thus, sufficient to construct a network that satisfies IL(H) Connect each X to every node in the minimal set Y s. t. : {(X U-{X}-Y|Y) : X H} Theorem: network is minimal and unique I-map

Markov Network Parameterization n Markov networks have too many degrees of freedom n n A clique over binary variables has 2 n parameters but the joint has only 2 n-1 parameters A The network A—B—C has clique {A, B} and {B, C} n n Both capture information on B which we can choose where we want to encode (in which clique) We can add/subtract between the cliques B C n Need: conventions for avoiding ambiguity in parameterization n Can be done using a canonical parameterization (see handout for details)

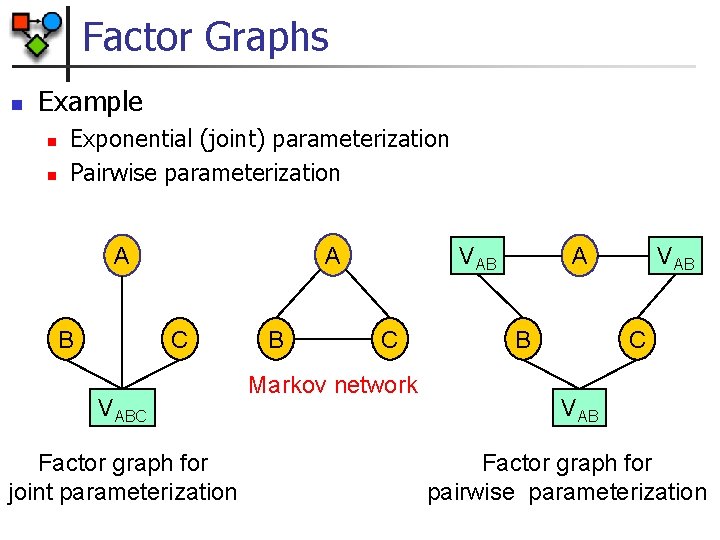
Factor Graphs n From the Markov network structure we do not know whether parameterization involves maximal cliques n n Example: fully connected graph may be pairwise potentials or one large (exponential) potential over all nodes Solution: Factor Graphs n n Undirected graph Two types of nodes n n n Variable nodes Factor nodes Parameterization n n Each factor node is associated with exactly one factor Scope of factor are all neighbor variables of the factor node

Factor Graphs n Example n n Exponential (joint) parameterization Pairwise parameterization A A B C VABC Factor graph for joint parameterization B A VAB C Markov network B VAB C VAB Factor graph for pairwise parameterization

Local Structure n Factor graphs still encode complete tables n n n Goal: as in Bayesian networks, represent context-specificity A feature [D] on variables D is an indicator function that for some y D: A distribution P is a log-linear model over H if it has n n Features 1[D 1], . . . , k[Dk] where each Di is a subclique in H A set of weights w 1, . . . , wk such that

Feature Representation n Several features can be defined on one subclique n n n any factor can be represented by features, where in the most general case we define a feature and weight for each entry in the factor Log-linear model is more compact for many distributions especially with large domain variables Representation is intuitive and modular n Features can be modularly added between any interacting sets of variables

Markov Network Parameterizations n Choice 1: Markov network n n n Choice 2: Factor graph n n n Product over graphs Useful for inference (later) Choice 3: Log-linear model n n Product over potentials Right representation for discussing independence queries Product over feature weights Useful for discussing parameterizations Useful for representing context specific structures All parameterizations are interchangeable

Domain Application: Vision n The image segmentation problem n n Task: Partition an image into distinct parts of the scene Example: separate water, sky, background

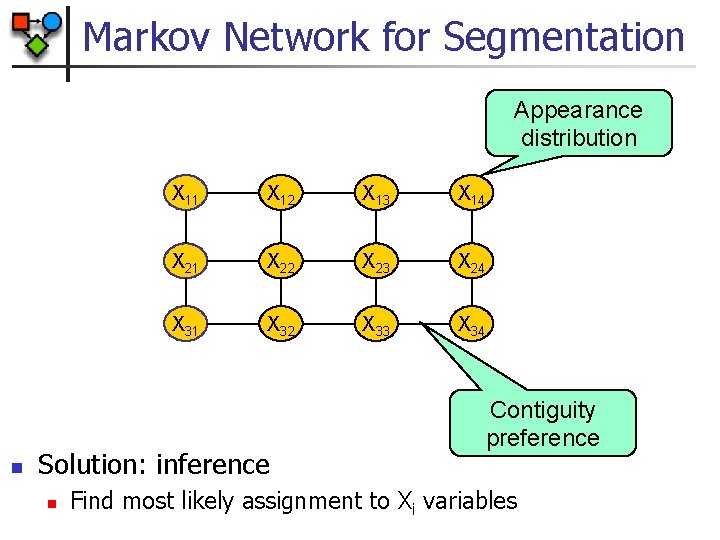
Markov Network for Segmentation n n Grid structured Markov network Random variable Xi corresponds to pixel i n n Neighboring pixels are connected in the network Appearance distribution n Domain is {1, . . . K} Value represents region assignment to pixel i wik – extent to which pixel i “fits” region k (e. g. , difference from typical pixel for region k) Introduce node potential exp(-wik 1{Xi=k}) Edge potentials n Encodes contiguity preference by edge potential exp( 1{Xi=Xj}) for >0

Markov Network for Segmentation Appearance distribution n X 11 X 12 X 13 X 14 X 21 X 22 X 23 X 24 X 31 X 32 X 33 X 34 Solution: inference n Contiguity preference Find most likely assignment to Xi variables

From Bayesian nets to Markov nets n Goal: build a Markov network H capable of representing any distribution P that factorizes over G n n Equivalent to requiring I(H) I(G) Construction process n n Connect each X to every node in the smallest set Y s. t. : {(X U-{X}-Y|Y) : X H} How can we find Y by querying G?

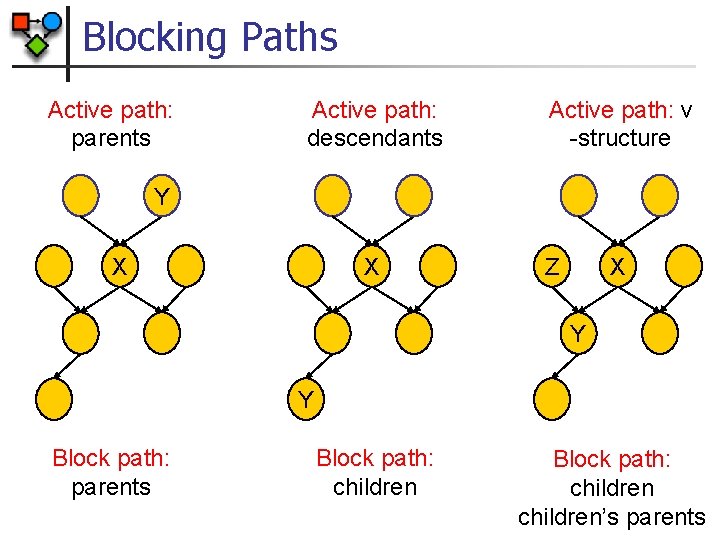
Blocking Paths Active path: parents Active path: descendants Active path: v -structure Y X X Z X Y Y Block path: parents Block path: children’s parents

From Bayesian nets to Markov nets n Goal: build a Markov network H capable of representing any distribution P that factorizes over G n n Equivalent to requiring I(H) I(G) Construction process n n Connect each X to every node in the smallest set Y s. t. : {(X U-{X}-Y|Y) : X H} How can we find Y by querying G? n Y = Markov blanket of X in G (parents, children’s parents)

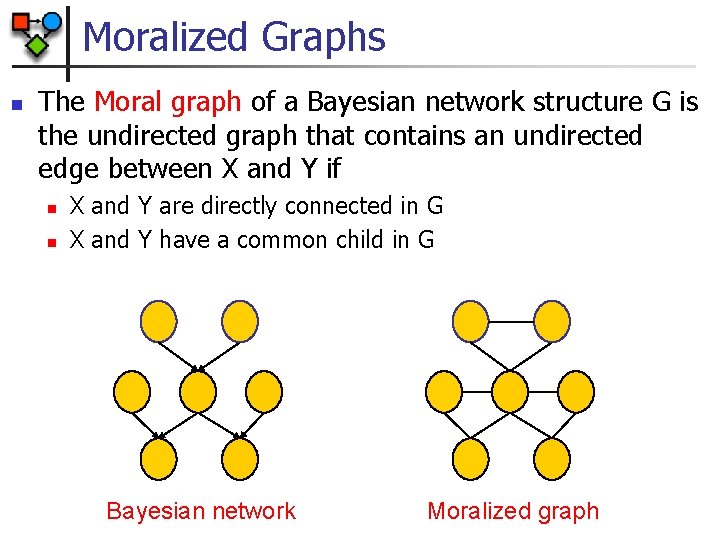
Moralized Graphs n The Moral graph of a Bayesian network structure G is the undirected graph that contains an undirected edge between X and Y if n n X and Y are directly connected in G X and Y have a common child in G Bayesian network Moralized graph

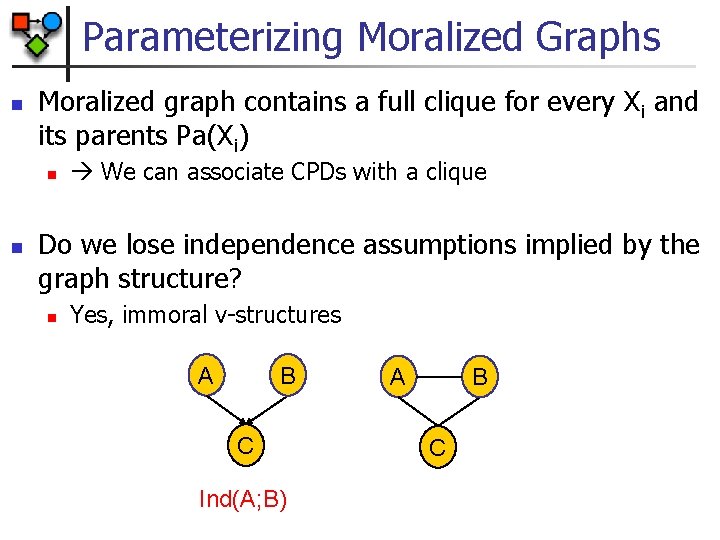
Parameterizing Moralized Graphs n Moralized graph contains a full clique for every Xi and its parents Pa(Xi) n n We can associate CPDs with a clique Do we lose independence assumptions implied by the graph structure? n Yes, immoral v-structures A B C Ind(A; B) A B C

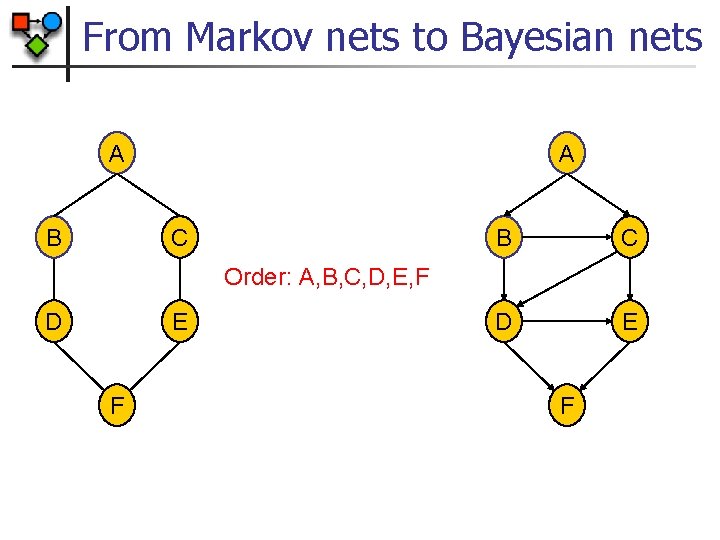
From Markov nets to Bayesian nets n n Transformation is more difficult and the resulting network can be much larger than the Markov network Construction algorithm n n n Use Markov network as template for independencies Fix ordering of nodes Add each node along with its minimal parent set according to the independencies defined in the distribution

From Markov nets to Bayesian nets A B A C B C D E Order: A, B, C, D, E, F D E F F

Chordal Graphs n n n Let X 1—X 2—. . . —Xk—X 1 be a loop in the graph A chord in the loop is an edge connecting Xi and Xj for two nonconsecutive nodes Xi and Xj An undirected graph is chordal if any loop X 1—X 2—. . . —Xk—X 1 for k 4 has a chord n n n That is, longest minimal loop is a triangle Chordal graphs are often called triangulated A directed graph is chordal if its underlying undirected graph is chordal

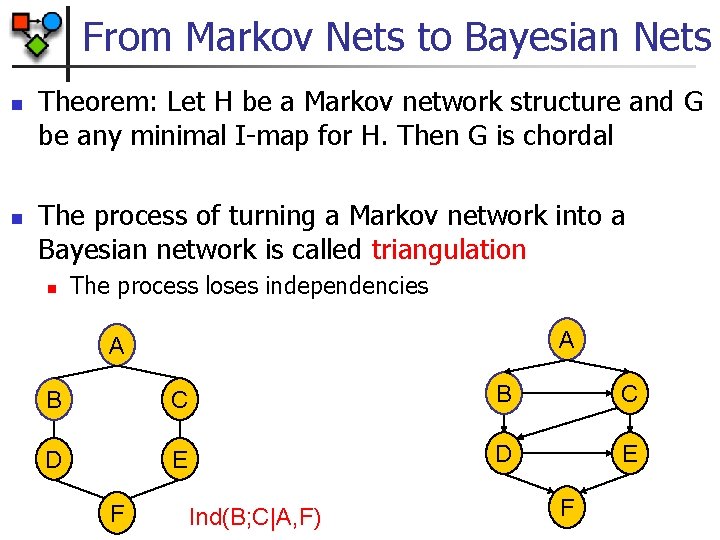
From Markov Nets to Bayesian Nets n n Theorem: Let H be a Markov network structure and G be any minimal I-map for H. Then G is chordal The process of turning a Markov network into a Bayesian network is called triangulation n The process loses independencies A A B C D E F Ind(B; C|A, F) F

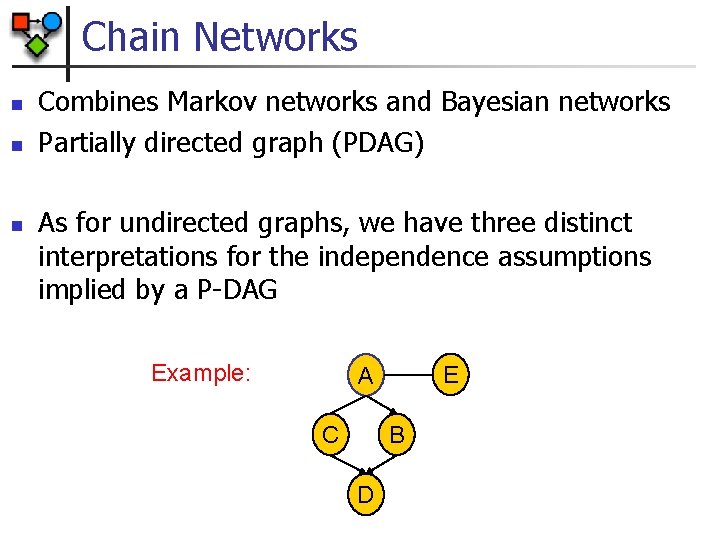
Chain Networks n n n Combines Markov networks and Bayesian networks Partially directed graph (PDAG) As for undirected graphs, we have three distinct interpretations for the independence assumptions implied by a P-DAG Example: E A C B D

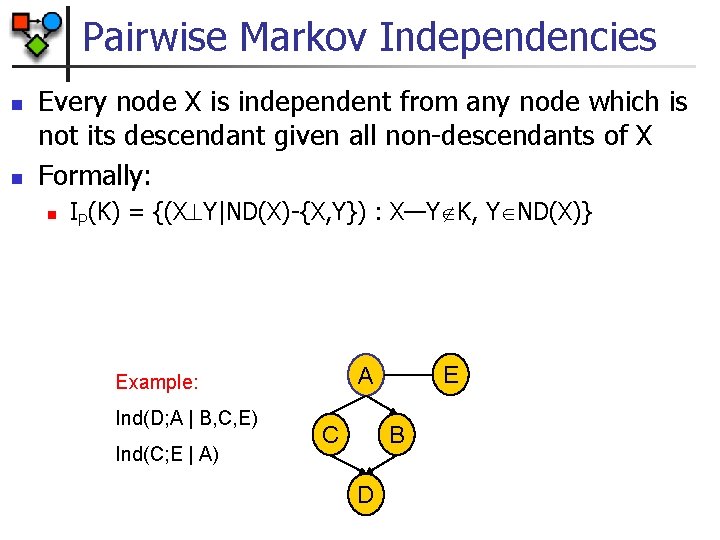
Pairwise Markov Independencies n n Every node X is independent from any node which is not its descendant given all non-descendants of X Formally: n IP(K) = {(X Y|ND(X)-{X, Y}) : X—Y K, Y ND(X)} Ind(D; A | B, C, E) Ind(C; E | A) E A Example: C B D

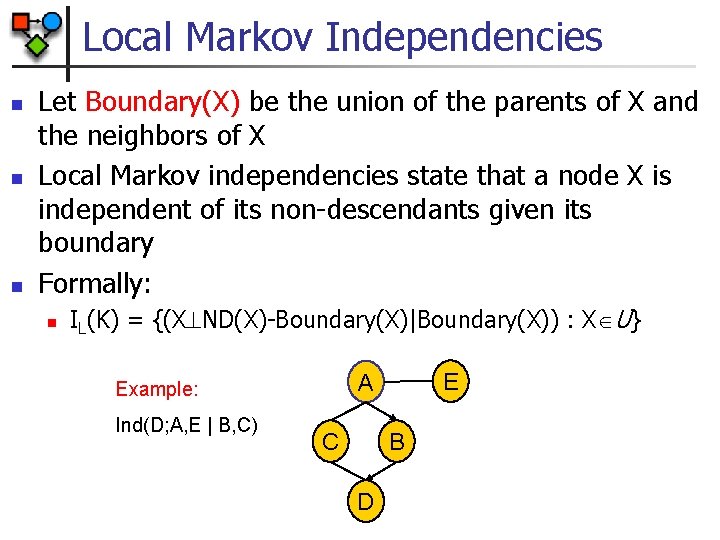
Local Markov Independencies n n n Let Boundary(X) be the union of the parents of X and the neighbors of X Local Markov independencies state that a node X is independent of its non-descendants given its boundary Formally: n IL(K) = {(X ND(X)-Boundary(X)|Boundary(X)) : X U} Ind(D; A, E | B, C) E A Example: C B D

Global Independencies n n n I(K) = {(X Y|Z) : X, Y, Z, X is c-separated from Y given Z} X is c-separated from Y given Z if X is separated from Y given Z in the undirected moralized graph M[K] The moralized graph of a P-DAG K is an undirected graph M[K] by n n Connecting any pair of parents of a given node Converting all directed edges to undirected edges For positive distributions: I(K) IL(K) IP(K)

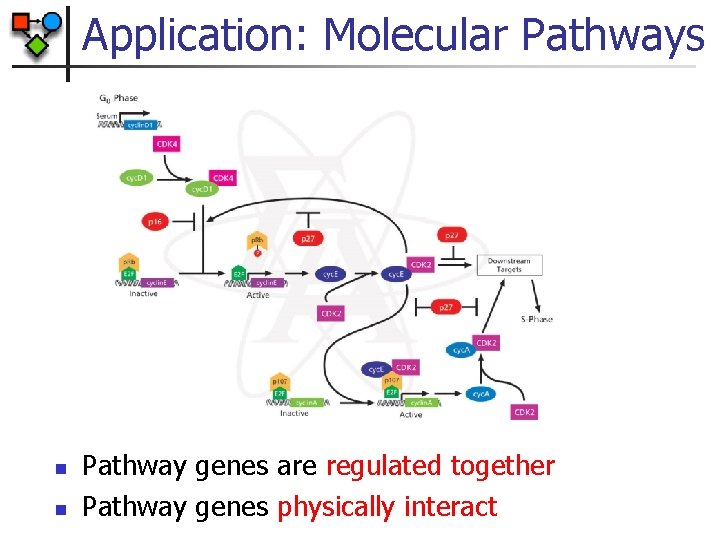
Application: Molecular Pathways n n Pathway genes are regulated together Pathway genes physically interact

Goal n Automatic discovery of molecular pathways: sets of genes that n n Are regulated together Physically interact

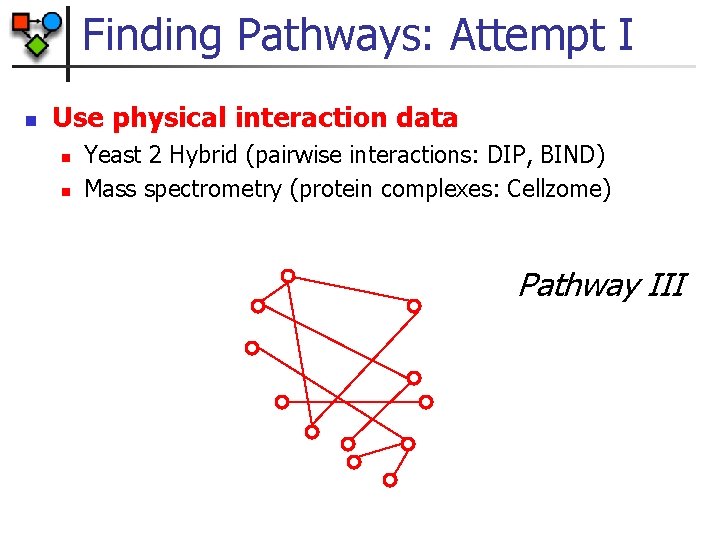
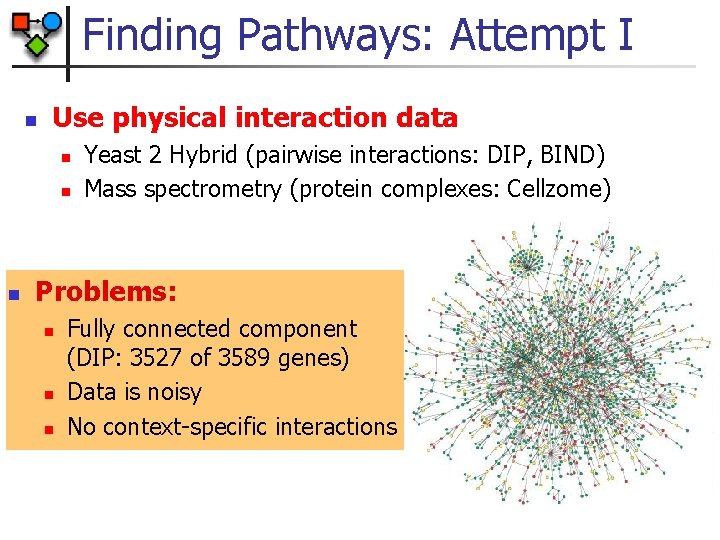
Finding Pathways: Attempt I n Use physical interaction data n n Yeast 2 Hybrid (pairwise interactions: DIP, BIND) Mass spectrometry (protein complexes: Cellzome) Pathway III

Finding Pathways: Attempt I n Use physical interaction data n n n Yeast 2 Hybrid (pairwise interactions: DIP, BIND) Mass spectrometry (protein complexes: Cellzome) Problems: n n n Fully connected component (DIP: 3527 of 3589 genes) Data is noisy No context-specific interactions

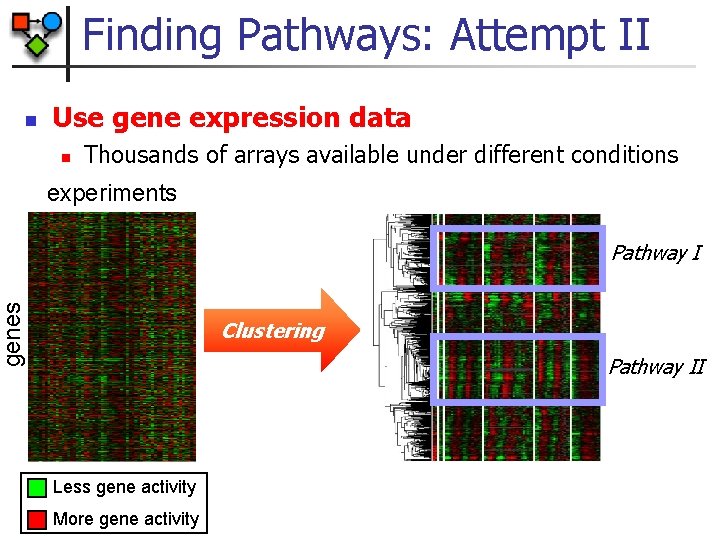
Finding Pathways: Attempt II Use gene expression data n Thousands of arrays available under different conditions experiments Pathway I genes n Clustering Pathway II Less gene activity More gene activity

Finding Pathways: Attempt II n Use gene expression data n n Thousands of arrays available under different conditions Problems: n n n Expression is only ‘weak’ indicator of interaction Data is noisy Interacting pathways are not separable Pathway II

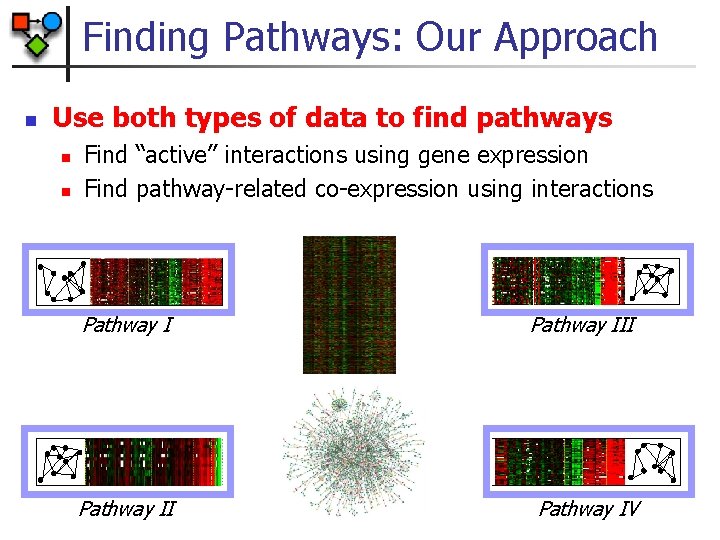
Finding Pathways: Our Approach n Use both types of data to find pathways n n Find “active” interactions using gene expression Find pathway-related co-expression using interactions Pathway III Pathway IV

Probabilistic Model n Genes are partitioned into “pathways”: n n n Expression component: n n Every gene is assigned to one of ‘k’ pathways Random variable for each gene with domain {1, …, k} Model likelihood is higher when genes in the same pathway have similar expression profiles Interaction component: n Model likelihood is higher when genes in the same pathway interact

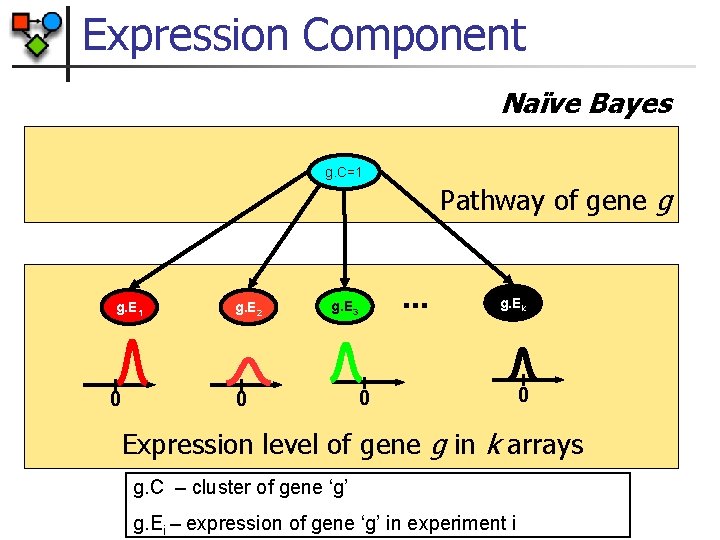
Expression Component Naïve Bayes g. C=1 Pathway of gene g g. E 1 0 g. E 2 … g. E 3 0 g. Ek 0 0 Expression level of gene g in k arrays g. C – cluster of gene ‘g’ g. Ei – expression of gene ‘g’ in experiment i

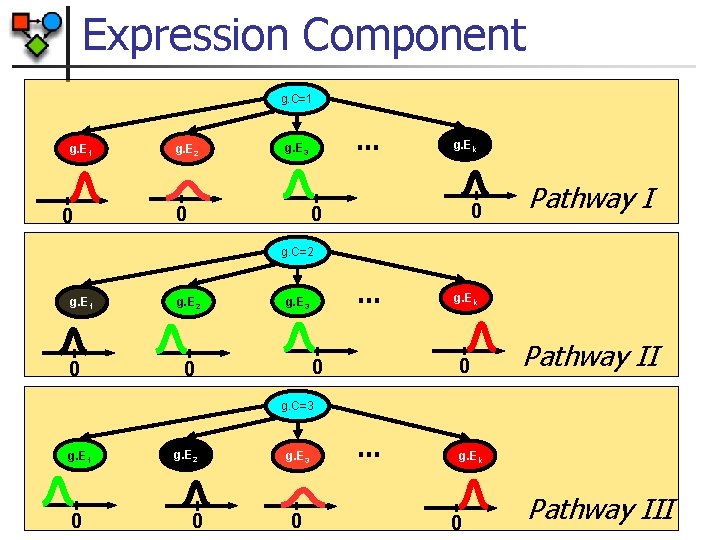
Expression Component g. C=1 g. E 1 0 g. E 2 … g. E 3 g. Ek 0 0 0 Pathway I g. C=2 g. E 1 0 g. E 2 … g. E 3 0 0 0 g. Ek Pathway II g. C=3 g. E 1 0 g. E 2 0 g. E 3 0 … g. Ek 0 Pathway III

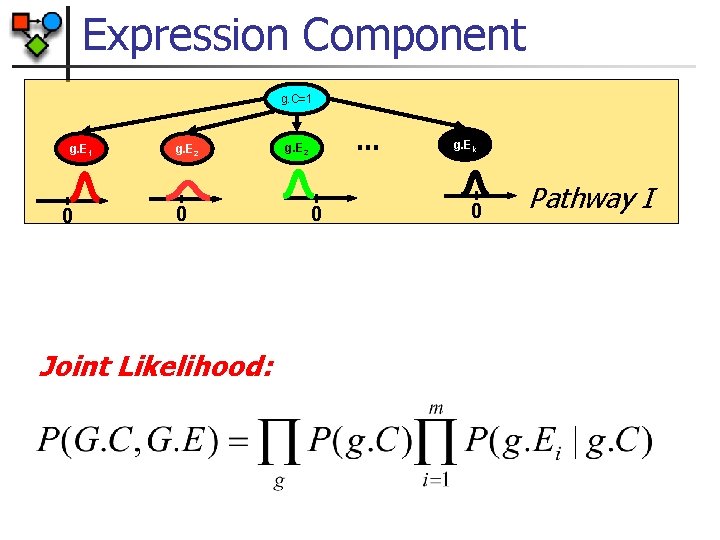
Expression Component g. C=1 g. E 1 0 g. E 2 0 Joint Likelihood: … g. E 2 0 g. Ek 0 Pathway I

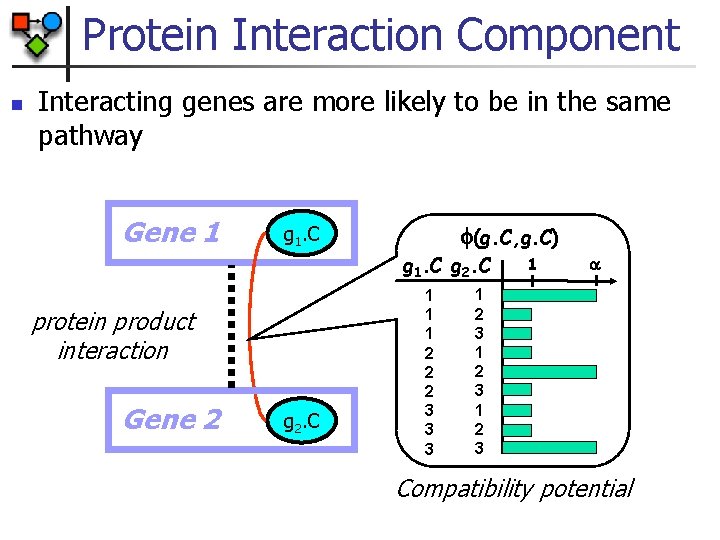
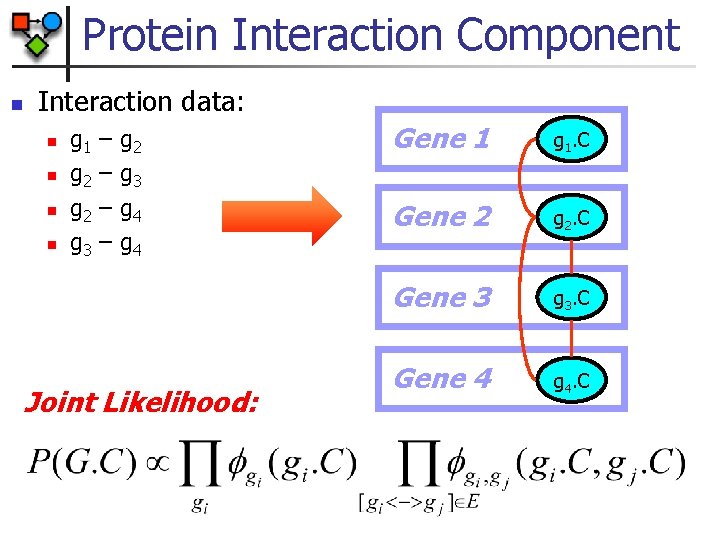
Protein Interaction Component n Interacting genes are more likely to be in the same pathway Gene 1 (g. C, g. C) g 1. C g 2. C protein product interaction Gene 2 g 2. C 1 1 1 2 2 2 3 3 3 1 1 2 3 Compatibility potential

Protein Interaction Component n Interaction data: n n g 1 g 2 g 3 – – g 2 g 3 g 4 Joint Likelihood: Gene 1 g 1. C Gene 2 g 2. C Gene 3 g 3. C Gene 4 g 4. C

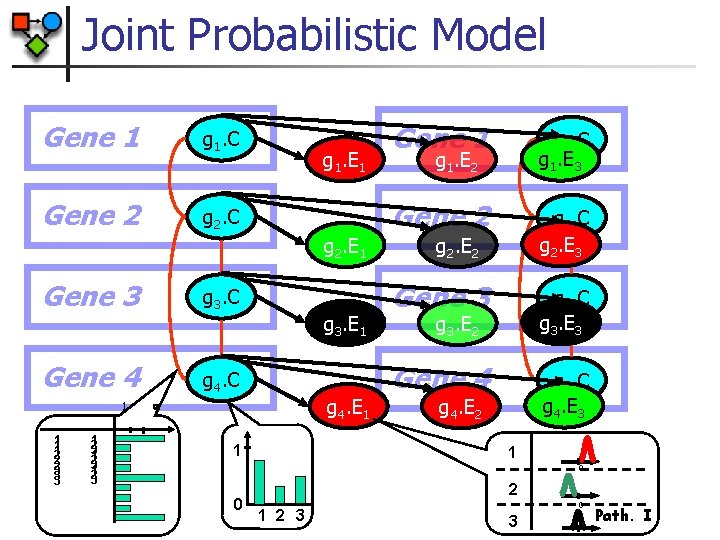
Joint Probabilistic Model Gene 1 g 1. C Gene 2 g 2. C g 1. E 1 g 2. E 1 Gene 3 g 3. C Gene 4 g 4. C 1 1 1 2 2 2 3 3 3 1 2 3 g 4. E 1 1 g 1. C g 1. E 3 Gene 2 g 2. C g 2. E 3 g 1. E 2 g 2. E 2 Gene 3 g 3. C g 3. E 3 Gene 4 g 4. C g 4. E 3 g 3. E 2 g 4. E 2 1 0 0 1 g 3. E 1 Gene 1 2 3 0 3 Path. I

Joint Probabilistic Model n Joint Likelihood: expression interactions

Model Involved n n Chain graph (directed and undirected edges) Hybrid network n n n Hidden and observed nodes n n n Discrete “cluster” variables Continuous expression variables Expression is observed Cluster variables are hidden Conditional Linear Gaussian CPDs n Expression given cluster variable

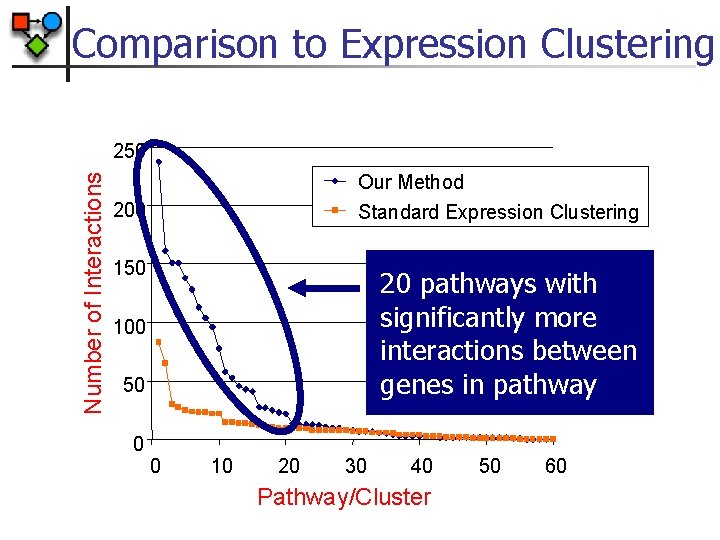
Comparison to Expression Clustering Number of Interactions 250 Our Method Standard Expression Clustering 200 150 20 pathways with significantly more interactions between genes in pathway 100 50 0 0 10 20 30 40 Pathway/Cluster 50 60

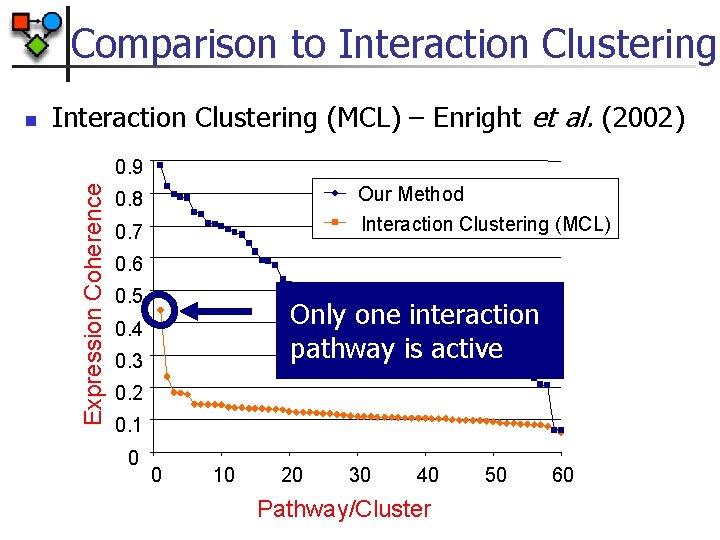
Comparison to Interaction Clustering (MCL) – Enright et al. (2002) 0. 9 Expression Coherence n Our Method Interaction Clustering (MCL) 0. 8 0. 7 0. 6 0. 5 Only one interaction pathway is active 0. 4 0. 3 0. 2 0. 1 0 0 10 20 30 40 Pathway/Cluster 50 60

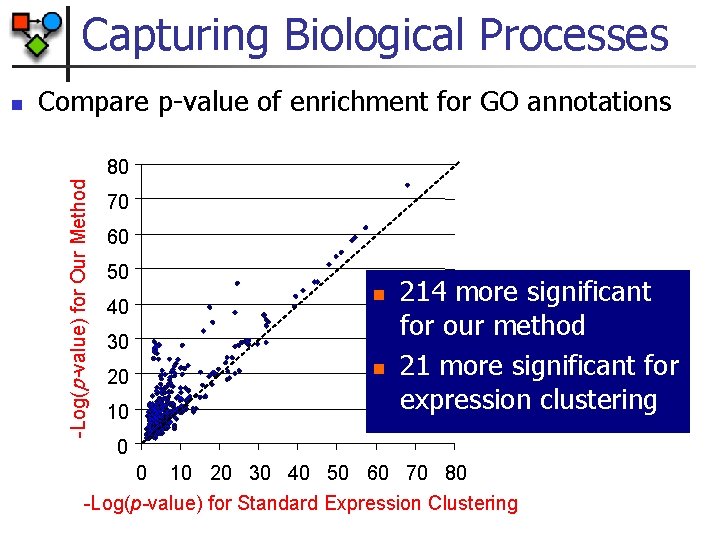
Capturing Biological Processes Compare p-value of enrichment for GO annotations 80 -Log(p-value) for Our Method n 70 60 50 n 40 30 n 20 10 214 more significant for our method 21 more significant for expression clustering 0 0 10 20 30 40 50 60 70 80 -Log(p-value) for Standard Expression Clustering

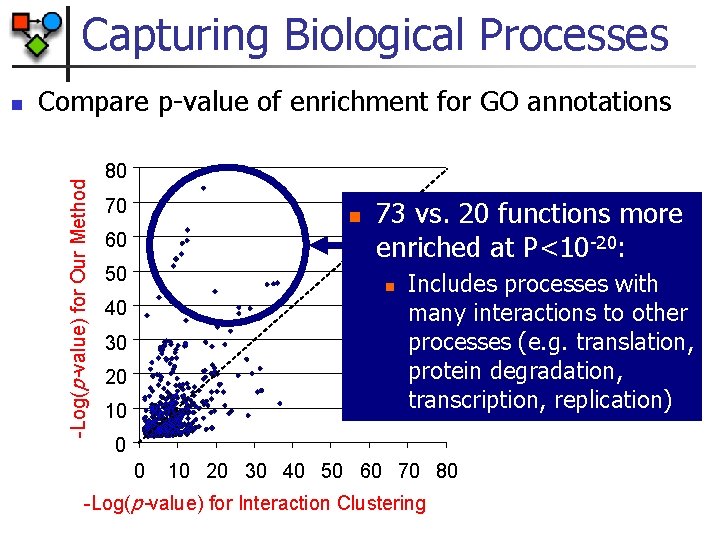
Capturing Biological Processes Compare p-value of enrichment for GO annotations -Log(p-value) for Our Method n 80 70 n 60 50 73 vs. 20 functions more enriched at P<10 -20: n 40 30 20 10 Includes processes with many interactions to other processes (e. g. translation, protein degradation, transcription, replication) 0 0 10 20 30 40 50 60 70 80 -Log(p-value) for Interaction Clustering

Summary n Markov Networks – undirected graphical models n n Relationship to Bayesian networks n n n Like Bayesian networks, define independence assumptions Three definitions exist, all equivalent in positive distributions Factorization is defined as product of factors over complete subsets of the graph Represent different families of independencies Independencies that can be represented in both – chordal graphs Moralized graphs n n Minimal network that represents Bayesnets dependencies d-separation in Bayesnets is equivalent to separation in moral graphs