Faculty of Mathematics and Computer Science The Weizmann

Faculty of Mathematics and Computer Science The Weizmann Institute of Science A Brief Introduction To Theory of Computer Science and The PCP Theorem By Dana Moshkovitz

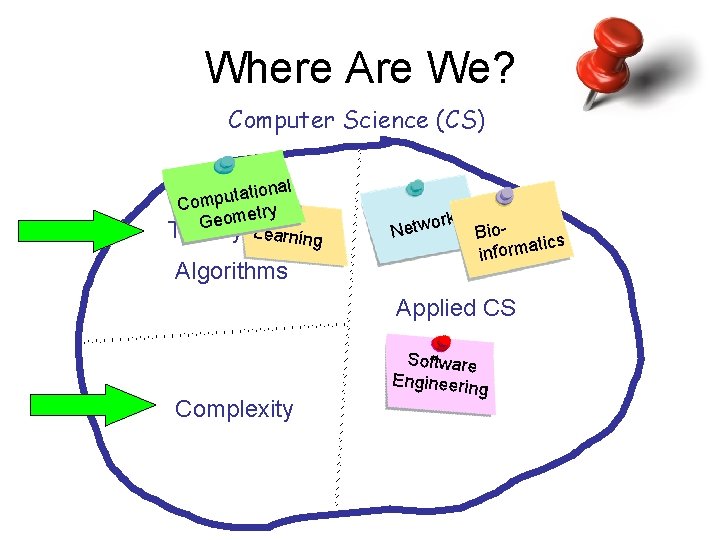
Where Are We? Computer Science (CS) nal o i t a t u Comp try Geome Theory of Lea. CS rning Algorithms orks iow t e N B tics a m r o f n i Applied CS Complexity Software Engineering

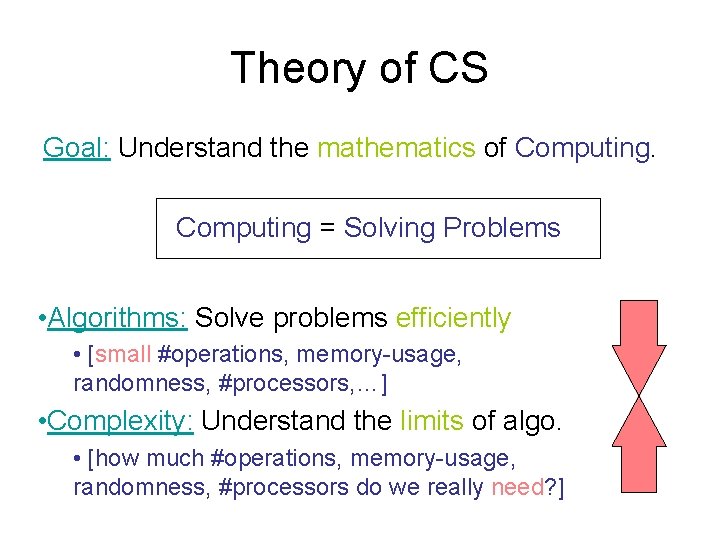
Theory of CS Goal: Understand the mathematics of Computing = Solving Problems • Algorithms: Solve problems efficiently • [small #operations, memory-usage, randomness, #processors, …] • Complexity: Understand the limits of algo. • [how much #operations, memory-usage, randomness, #processors do we really need? ]

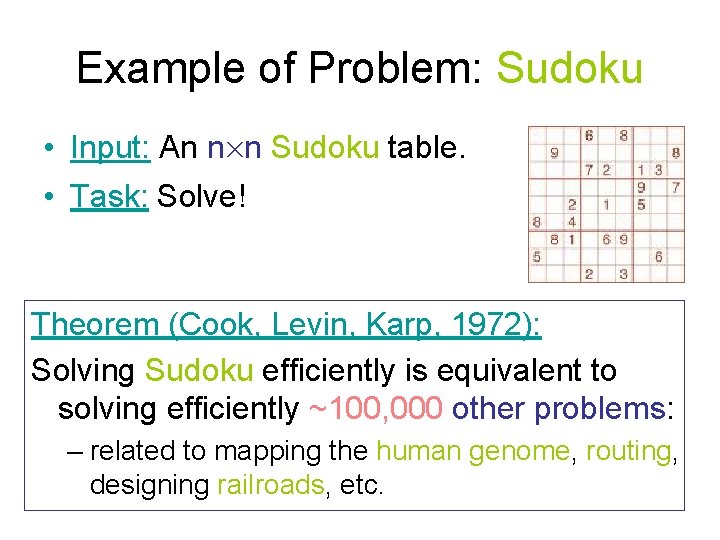
Example of Problem: Sudoku • Input: An n£n Sudoku table. • Task: Solve! Theorem (Cook, Levin, Karp, 1972): Solving Sudoku efficiently is equivalent to solving efficiently ~100, 000 other problems: – related to mapping the human genome, routing, designing railroads, etc.

What’s So Special In Sudoku? ? • if I know a solution for Sudoku, I can prove this to you! • Efficient Checking: Given my solution, you can check its validity efficiently. • The class of all problems having this property is called NP (= non-deterministic polynomial time).

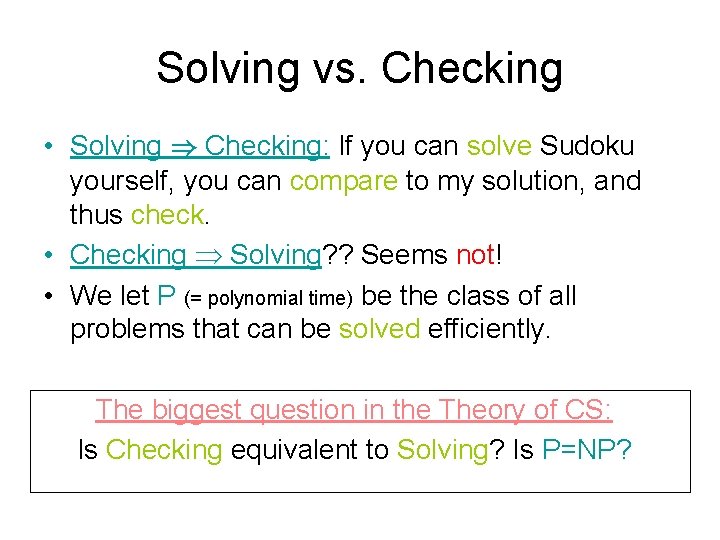
Solving vs. Checking So, what’s easier, solving or checking? Solving Checking

Solving vs. Checking • Solving ) Checking: If you can solve Sudoku yourself, you can compare to my solution, and thus check. • Checking Solving? ? Seems not! • We let P (= polynomial time) be the class of all problems that can be solved efficiently. The biggest question in the Theory of CS: Is Checking equivalent to Solving? Is P=NP?

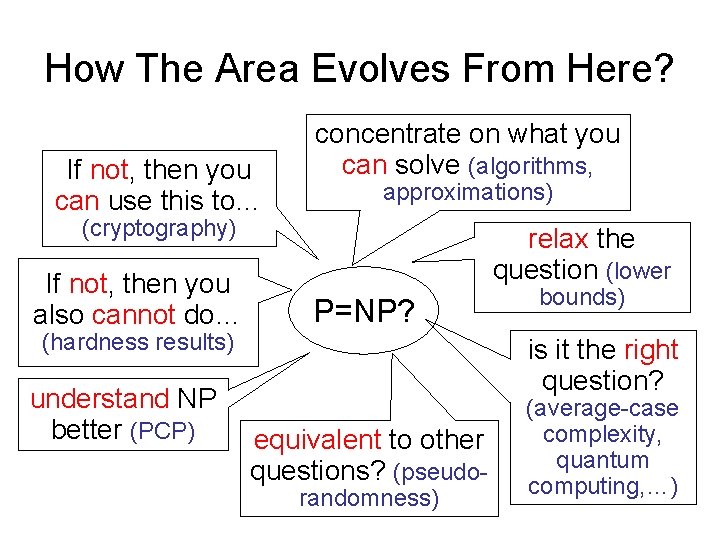
How The Area Evolves From Here? If not, then you can use this to… concentrate on what you can solve (algorithms, approximations) (cryptography) If not, then you also cannot do… (hardness results) understand NP better (PCP) relax the question (lower P=NP? bounds) is it the right question? equivalent to other questions? (pseudorandomness) (average-case complexity, quantum computing, …)

My Research: Understanding NP Better PCP (=probabilistically checkable proofs): Surprising characterization of NP. Even more important than first seems… • Cannot do: gives hardness of approximation. • Can do: gives new constructions.

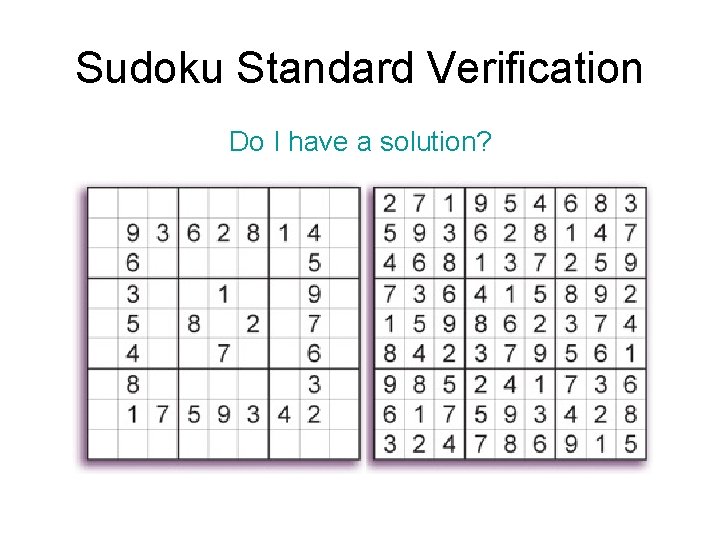
Sudoku Standard Verification Do I have a solution?

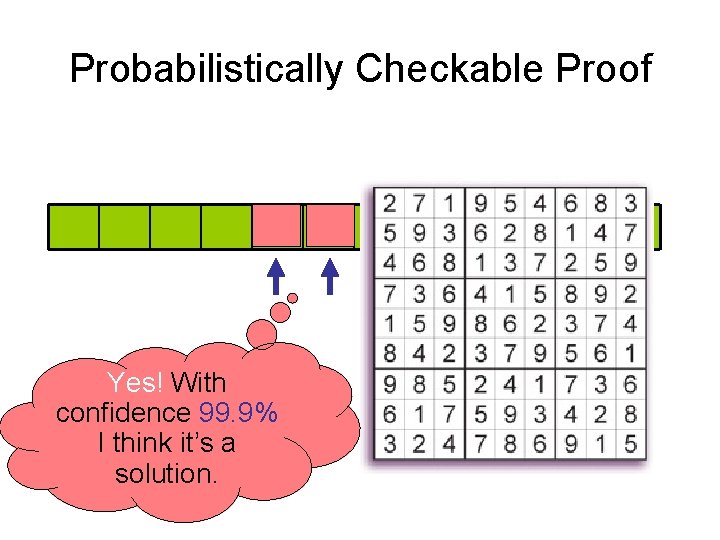
Probabilistically Checkable Proof Yes! With confidence 99. 9% I think it’s a solution.

PCP Theorem ([AS, ALMSS], 1992): Given any Sudoku riddle, given any solution, one can write the solution in a way that allows extremely fast verification: • verification by picking at random 2 places and checking only them!