Charm hadronic form factors with QCD sum rules

Charm hadronic form factors with QCD sum rules Motivation QCDSR Results on form factors Application: charmonium production Conclusion F. S. N. , M. Nielsen IFUSP (São Paulo) BRAZIL

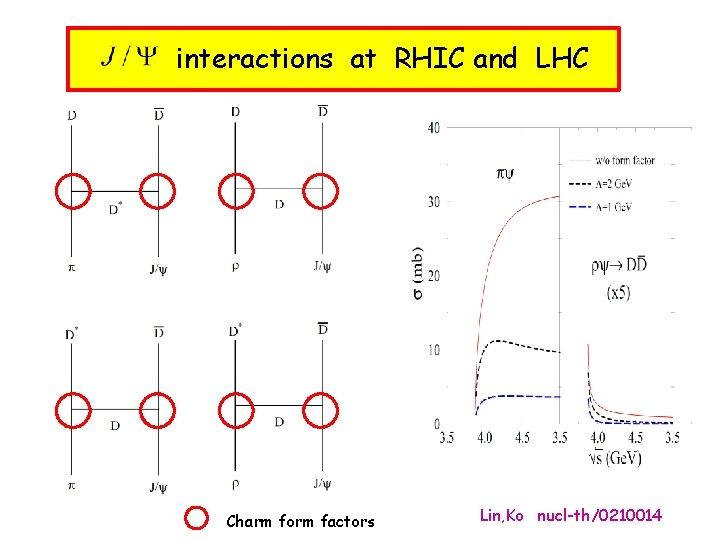
interactions at RHIC and LHC Charm form factors Lin, Ko nucl-th/0210014

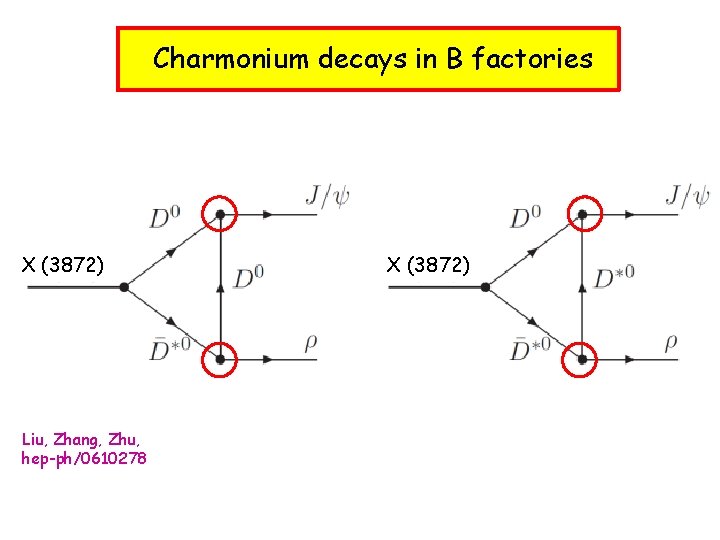
Charmonium decays in B factories X (3872) Liu, Zhang, Zhu, hep-ph/0610278 X (3872)

interactions at FAIR Haidenbauer, Krein, Meissner, Sibirtsev ar. Xiv: 0704. 3668 [nucl-th]

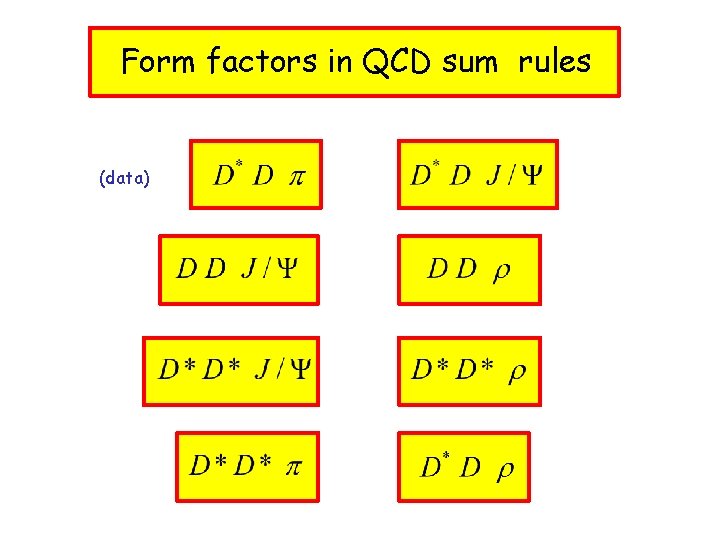
Form factors in QCD sum rules (data)

1) Write three-point correlation function: The QCD side (Operator Product Expansion side): 2) Choose the currents: 3) Insert the currents in and make the contractions:

4) Perform the OPE: The hadronic side (phenomenological side): 5) Insert hadronic states in + higher resonances

6) Use the matrix elements: 7) Use an effective Lagrangian to compute the amplitude: 8) Write

On both sides: 9) Decompose in tensor structures and choose one of them: 10) Write a double dispersion relation: 11) Identify 12) Apply a double Borel transform: double discontinuity

13) Write the sum rule: 14) Numerical analysis: Borel masses: Continuum thresholds : Numbers : or

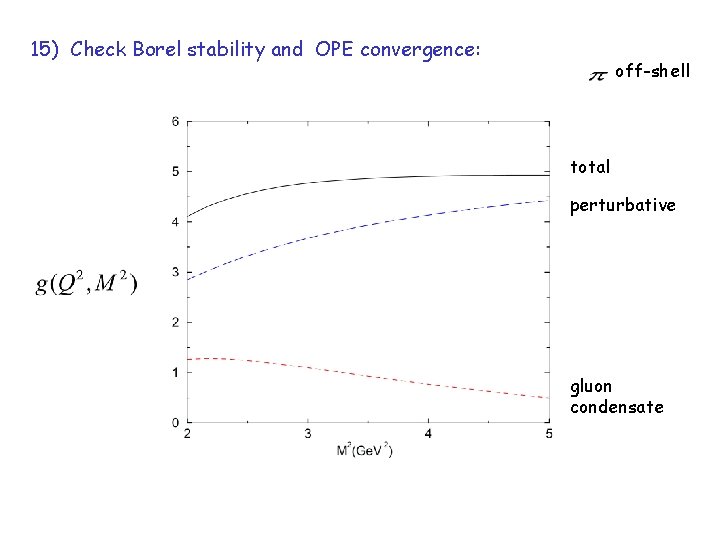
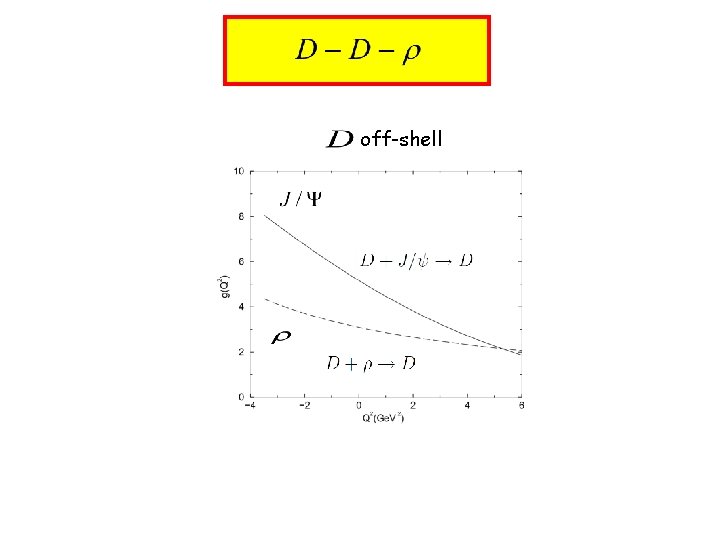
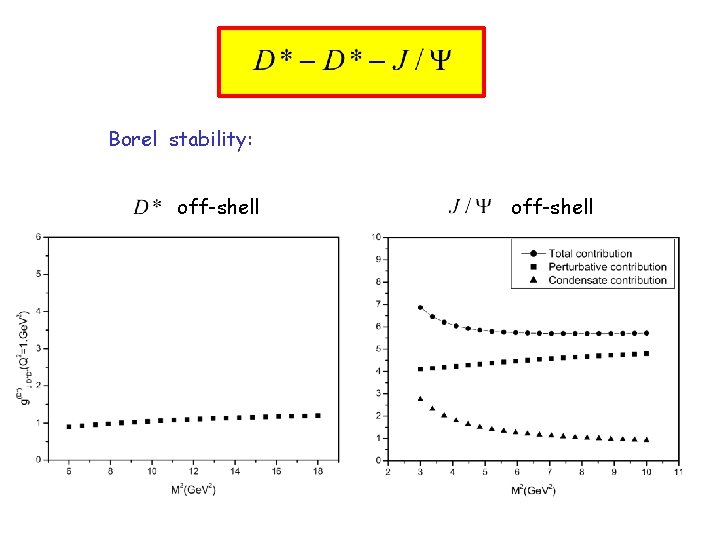
15) Check Borel stability and OPE convergence: off-shell total perturbative gluon condensate

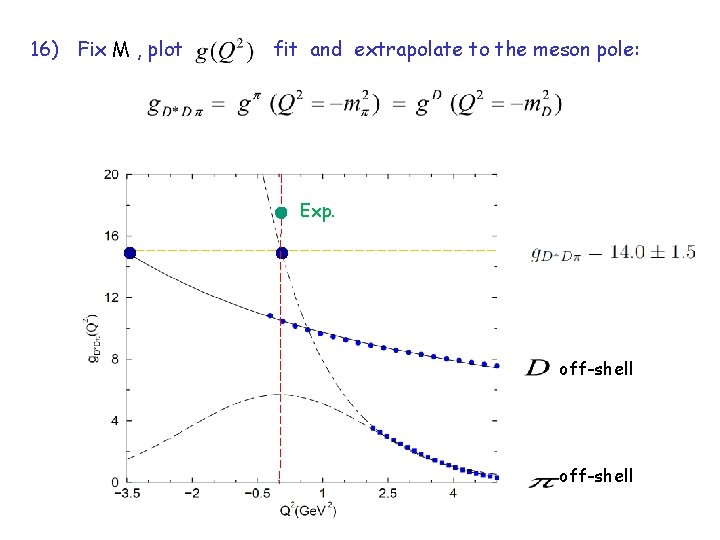
16) Fix M , plot fit and extrapolate to the meson pole: Exp. off-shell

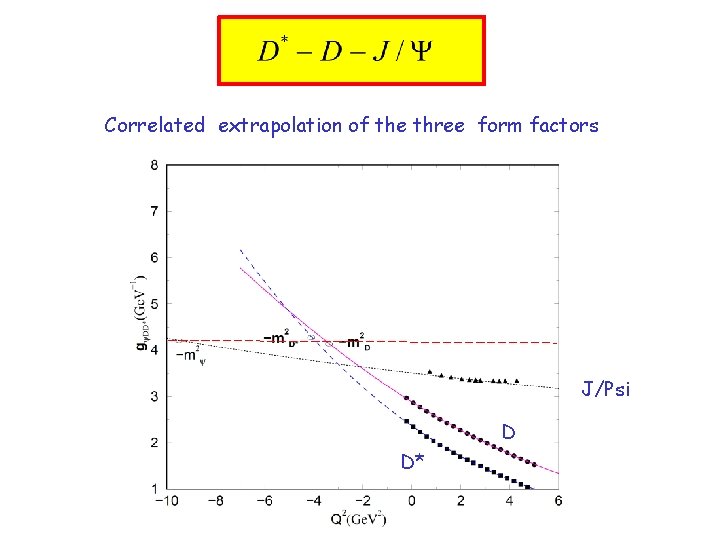
Correlated extrapolation of the three form factors J/Psi D D*

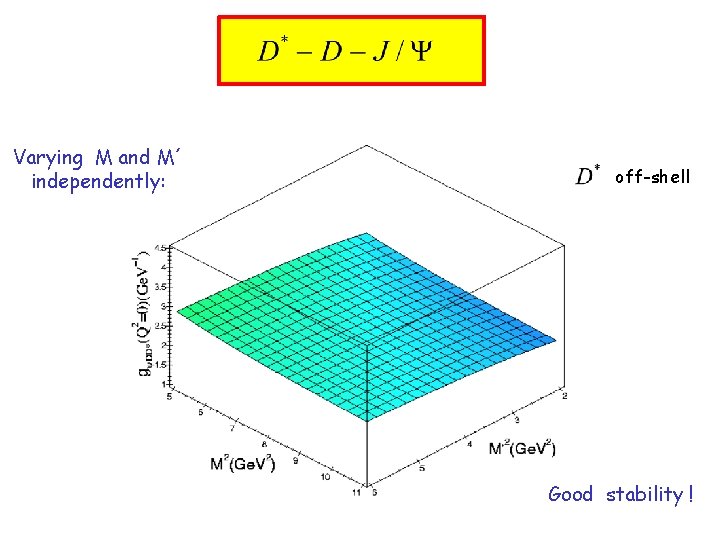
Varying M and M´ independently: off-shell Good stability !

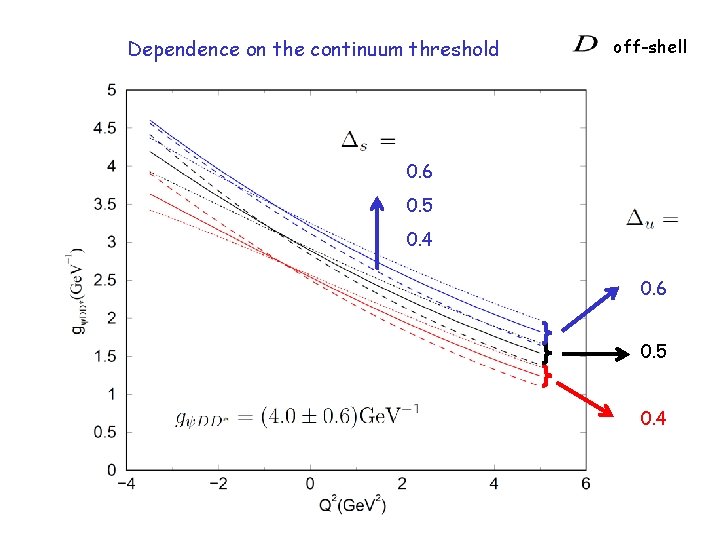
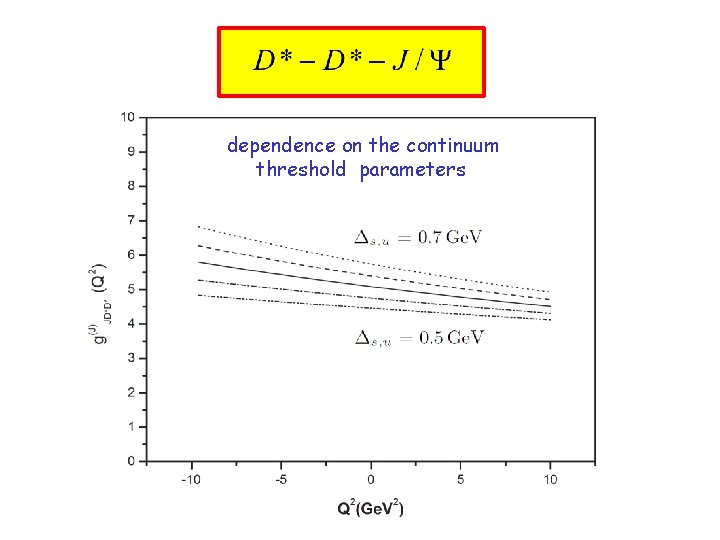
Dependence on the continuum threshold off-shell 0. 6 0. 5 0. 4

Couplings

Parametrizations:

Comments Coupling D*-D-pion compatible with data and with lattice QCD: data lattice Becirevic, Charles, Le Yaouanc, L. Olivier, Pene, Raynal, (2003) Compatibility with HQET relations : Oh, Lee, Song, PRC (2000) =

Application Charmonium production and absorption in nuclear matter Oh, Lee, Song, PRC (2000)

Application Charmonium production and absorption in nuclear matter “Charmonium regeneration”

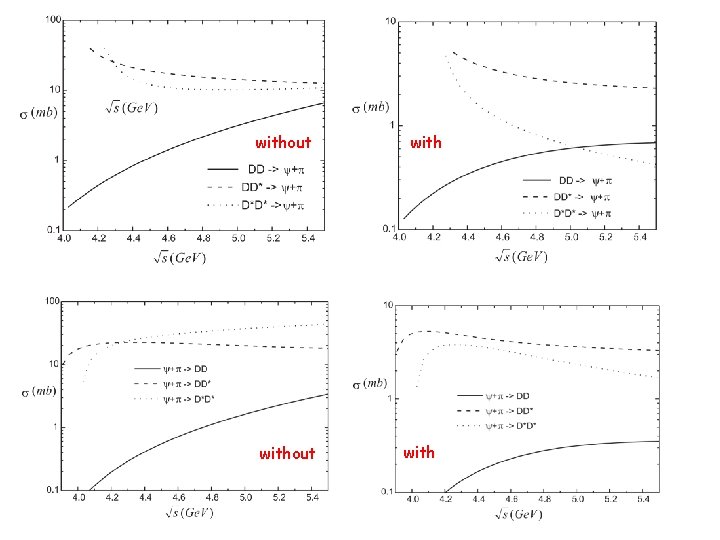
without with

Conclusion Charm form factors are still very usefull for phenomenology Charm form factors change calculations by one order of magnitude We can calculate them with QCDSR (finished the first round) The obtained coupling constants are of the same order of magnitude The numbers roughly agree with previous phenomenological estimates The form factors were used in one phenomenological application

References M. E. Bracco et al. , Phys. Lett. B 521, 1 (2001) R. D. Matheus et al. , Phys. Lett. B 541, 265 (2002) F. S. Navarra et al. , Phys. Rev. D 65, 037502 (2002) M. E. Bracco et al. , Phys. Lett. B 605, 326 (2005) F. Carvalho et al. , Phys. Rev. C 72, 024902 (2005) R. D. Matheus et al. , Int. J. Mod. Phys. E 14, 555 (2005) M. E. Bracco et al. , Phys. Lett. B 659, 559 (2008) B. Osorio Rodrigues et al. , ar. Xiv: 1003. 2604 [hep-ph]

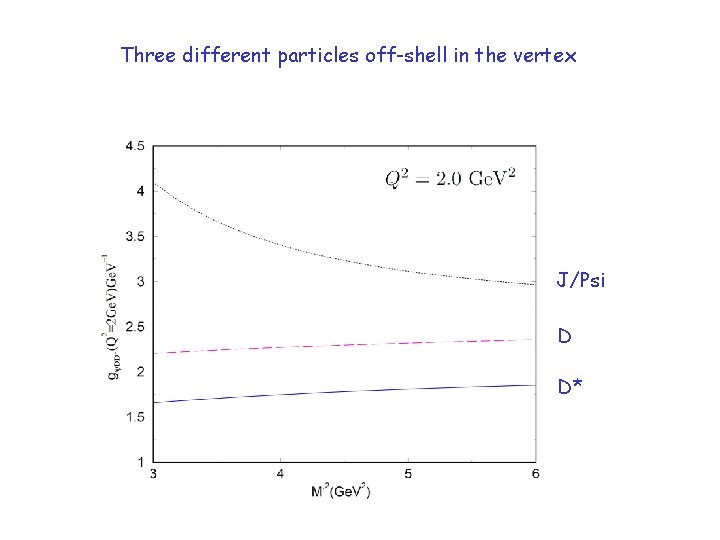
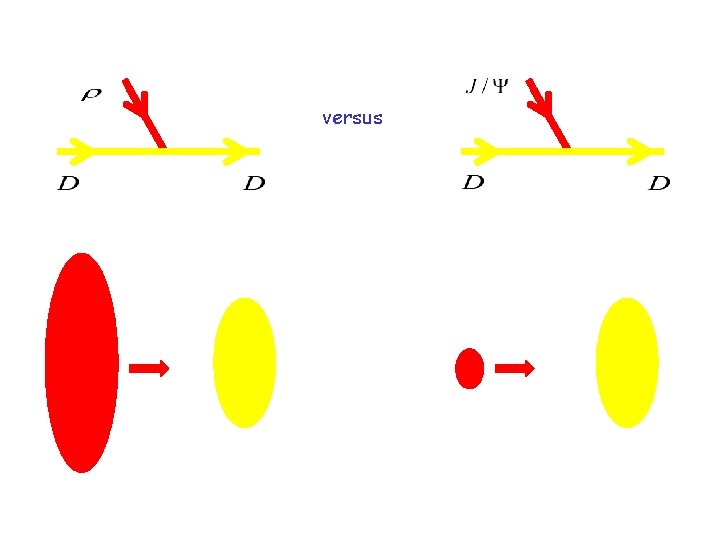
Three different particles off-shell in the vertex J/Psi D D*

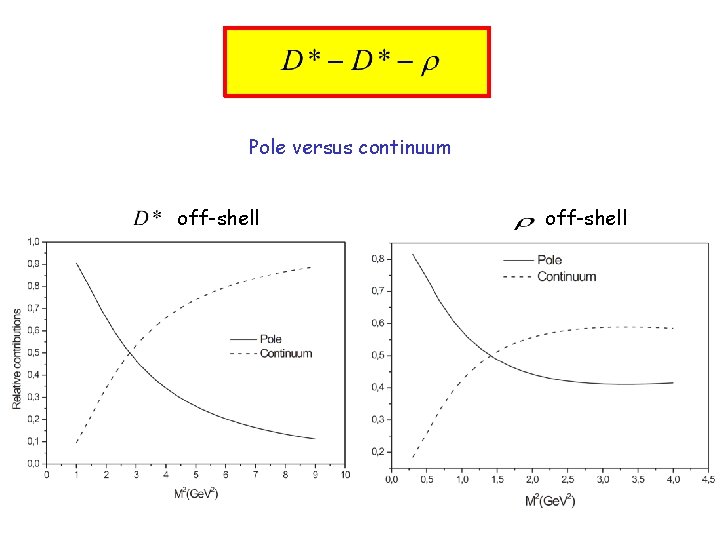
Pole versus continuum off-shell

Errors Truncation of the OPE corrections Choice of tensor structure Pole + continuum Ansatz ~ 20 % Continuum threshold parameters Values of masses and condensates Choice of Borel mass Medium effects Extrapolation to the mass shell ?

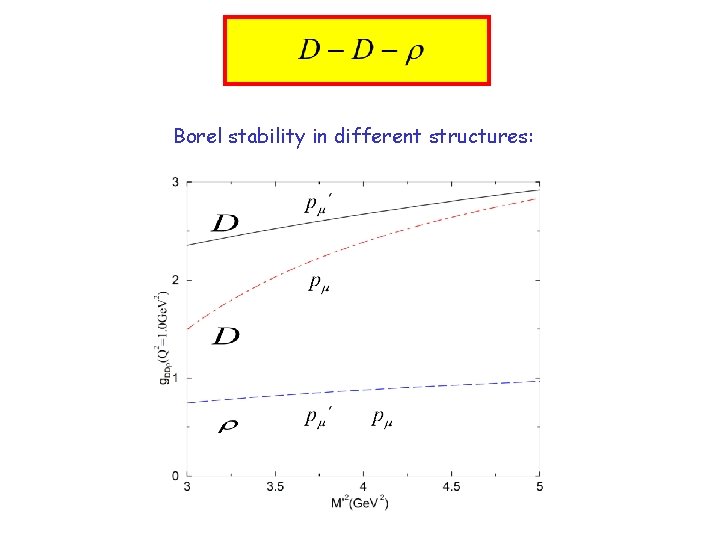
Borel stability in different structures:

14 tensor structures Choose

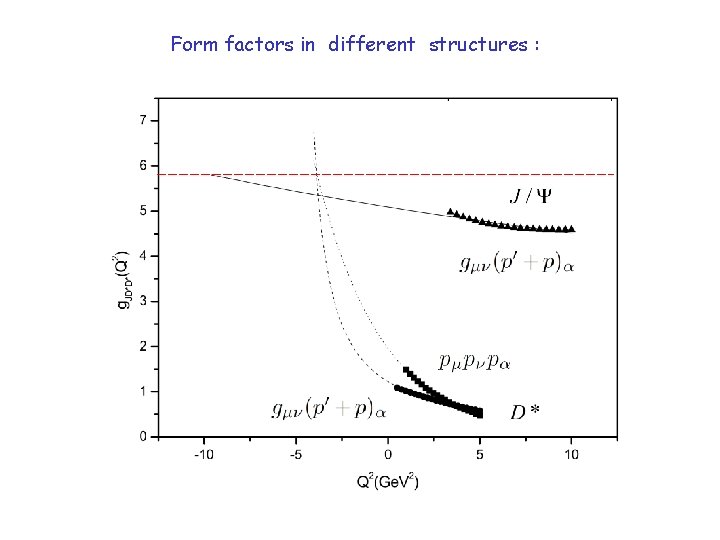
Form factors in different structures :

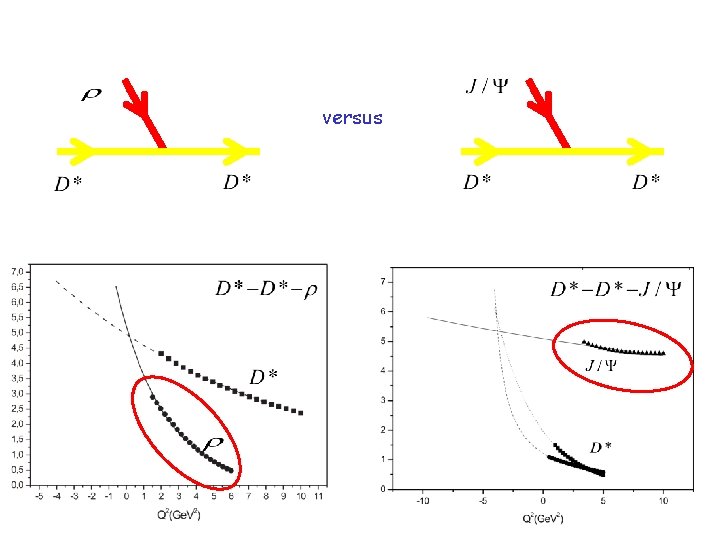
versus

Couplings with vector mesons Matinyann, Muller, PRC (1998) Oh, Lee, Song, PRC (2000) not very compatible with VDM estimates :

P 1

P 3

P 3

P 4

P 4

P 4

P 5

P 5

P 5 Sergei G. Matinyann, Berndt Muller Phys. Rev. C 58: 2994 -2997, 1998. nucl-th/9806027

P 6

P 6

Kodjamirian

P 7

P 8

P 10

Frequent questions Higher dimension condensates ? Infinities ? Killed by Imaginary Corr + Cutkosky + Borel + s 0 / QHD Differences between on and off-shell ? Only Borel ? Compatible with SU(4) ? HQET ? VMD? Pole versus continuum (well defined ? ) changes with Q 2 ? Extension to quartic couplings ? Why the restrictions in the Q 2 region ? Why not smaller Q 2 ? Final errors ? Observable applications ?

Back ups

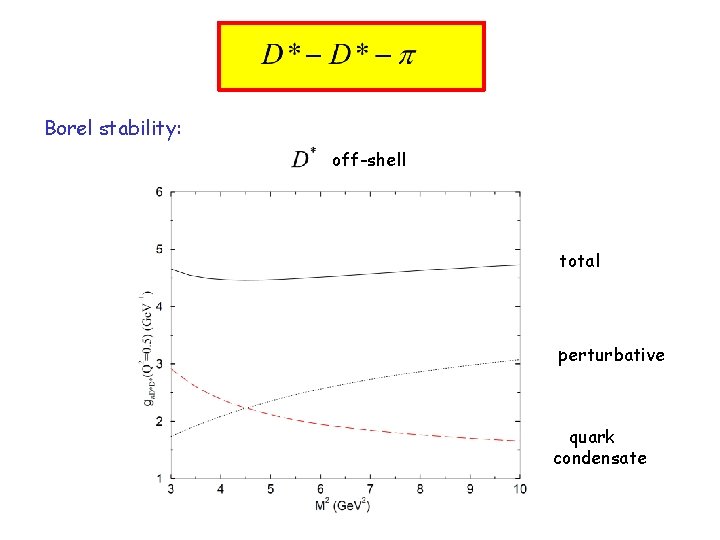
Borel stability: off-shell total perturbative quark condensate

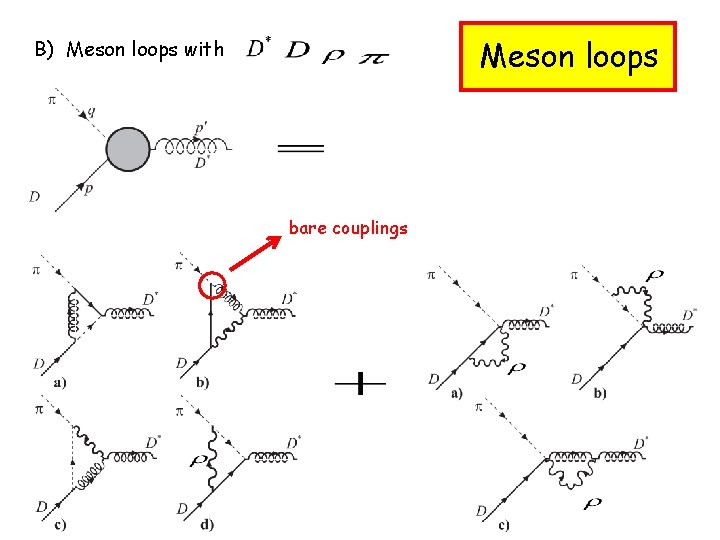
Meson loops B) Meson loops with bare couplings

Introduce the : Calculate the loops and compute the vertex function Calculate the form factor of an off-shell D: fitted to adjust QCDSR points

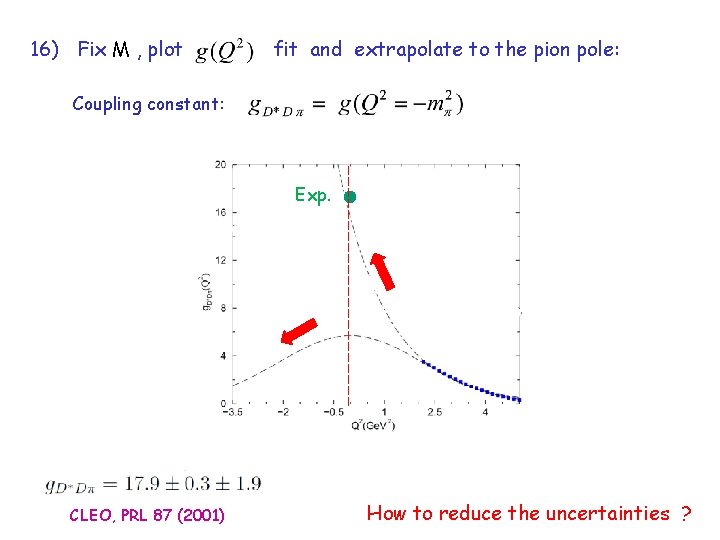
16) Fix M , plot fit and extrapolate to the pion pole: Coupling constant: Exp. CLEO, PRL 87 (2001) How to reduce the uncertainties ?

Three different particles off-shell in the vertex ! sum rules off-shell

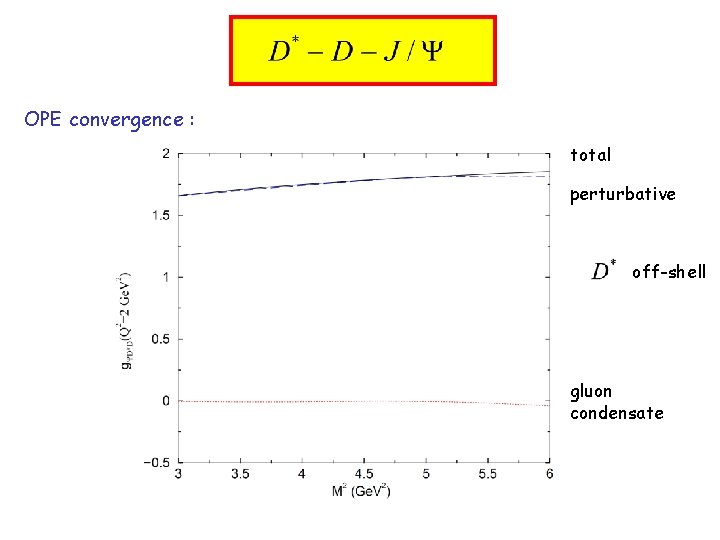
OPE convergence : total perturbative off-shell gluon condensate

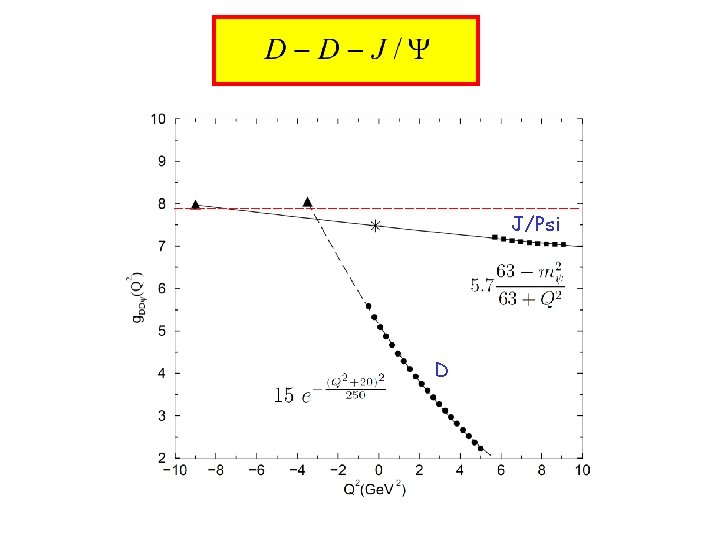
J/Psi D

Parametrizations:

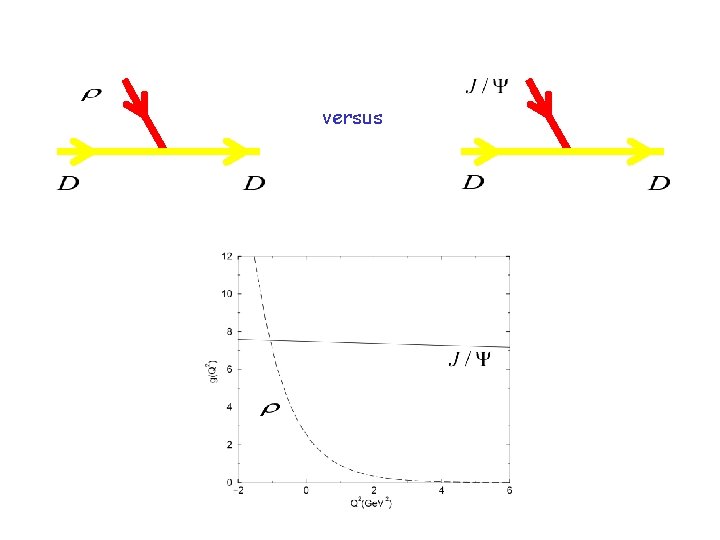
versus

versus

off-shell

Parametrizations:

Borel stability: off-shell

dependence on the continuum threshold parameters

Parametrizations: ( other structure )

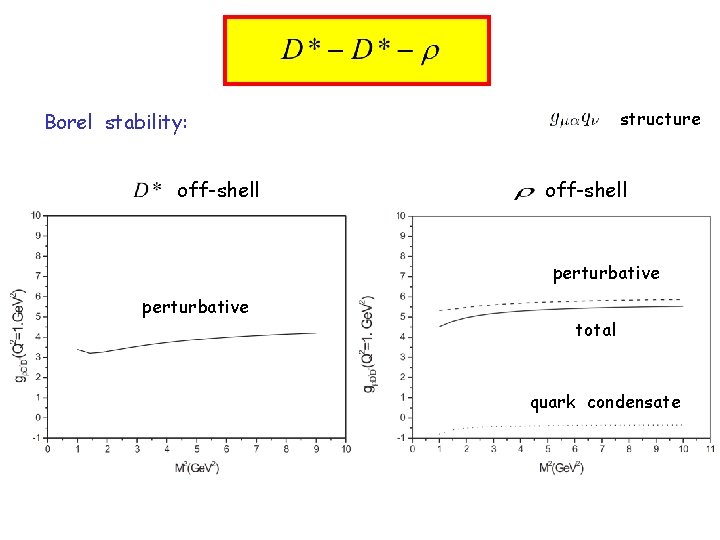
structure Borel stability: off-shell perturbative total quark condensate

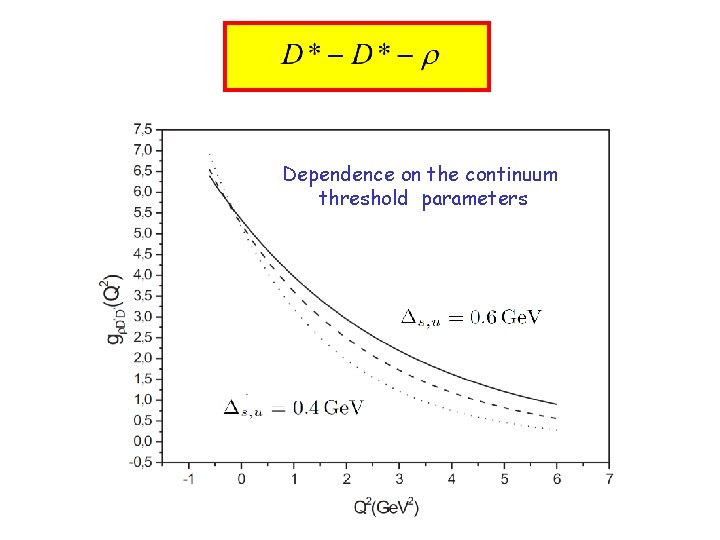
Dependence on the continuum threshold parameters

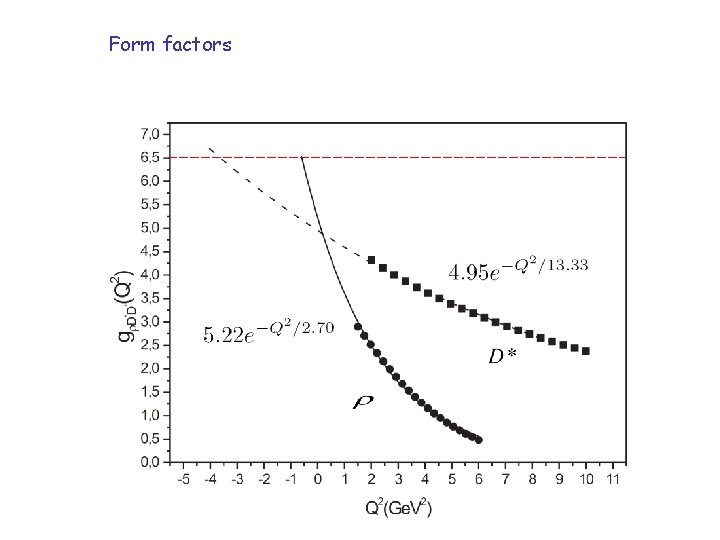
Form factors

Parametrizations:

Parametrizations:

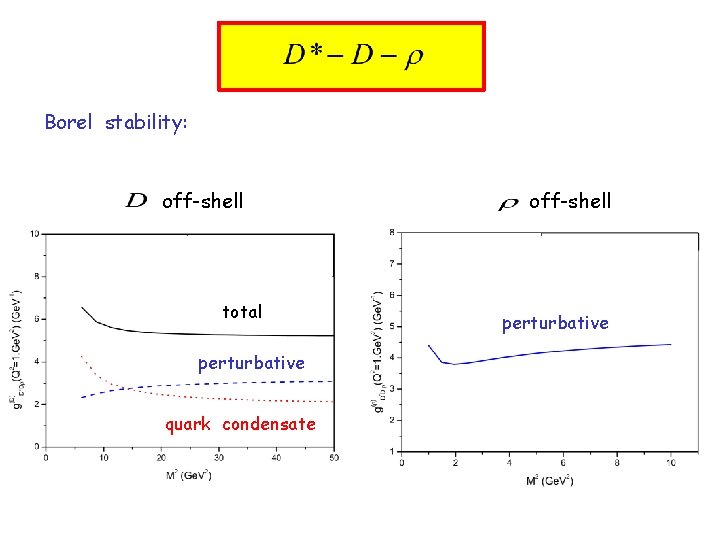
Borel stability: off-shell total perturbative quark condensate off-shell perturbative

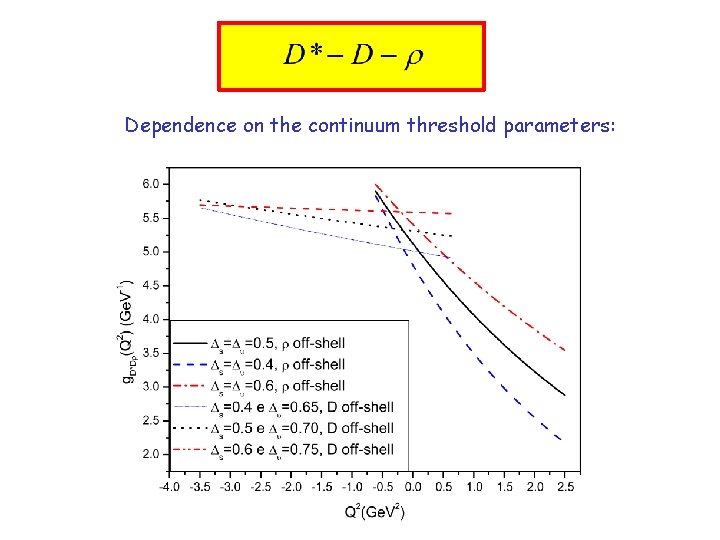
Dependence on the continuum threshold parameters:

Parametrizations:

List of form factors

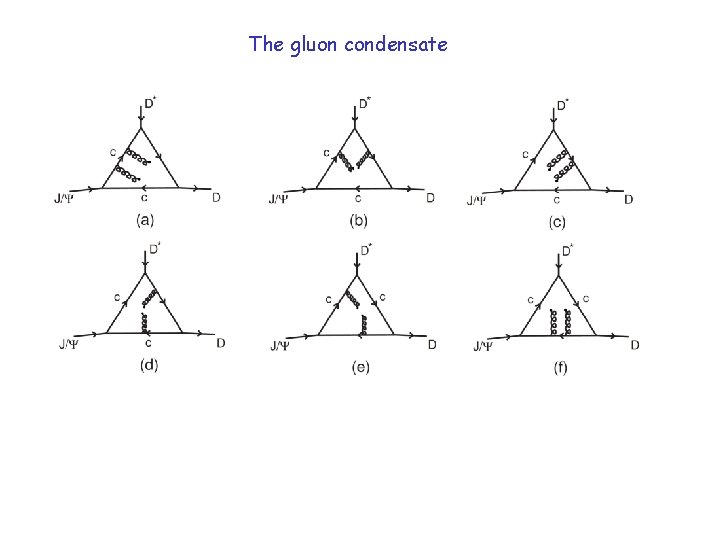
The gluon condensate

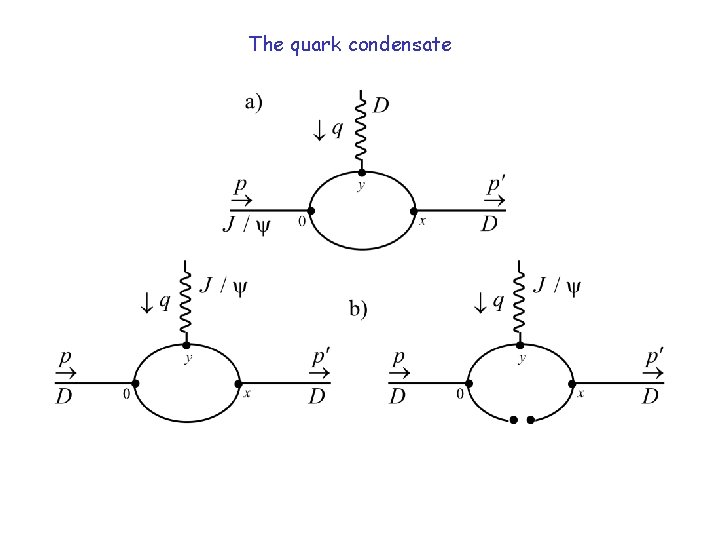
The quark condensate

Oh, Song, Lee, Wong, nucl-th/0205065 Oh, Song, Lee, Wong, nucl-th/0010064 Liu, Ko nucl-th/070277 Phys. Rev. C 75, 064903 Charm form factors Oh, Song, Lee, Wong, nucl-th/0205065

Conclusion Motivação D* D pi : dados, rede, mais calculos feitos, mais leve! D* D Psi: mais pesado! D D Psi e D D rho: comparação de sondas diferente ! D* D* Psi e D* D* rho: comparação de sondas diferente ! D* D* pi D* D rho Table. . .

Motivation Understand J/psi and D interactions in hadronic and nuclear matter Understand final state interactions in B decays and X(3872) decays In the strange sector: . . . Form factors: simple parametrizations fitted to data Monopole: Coupling constant

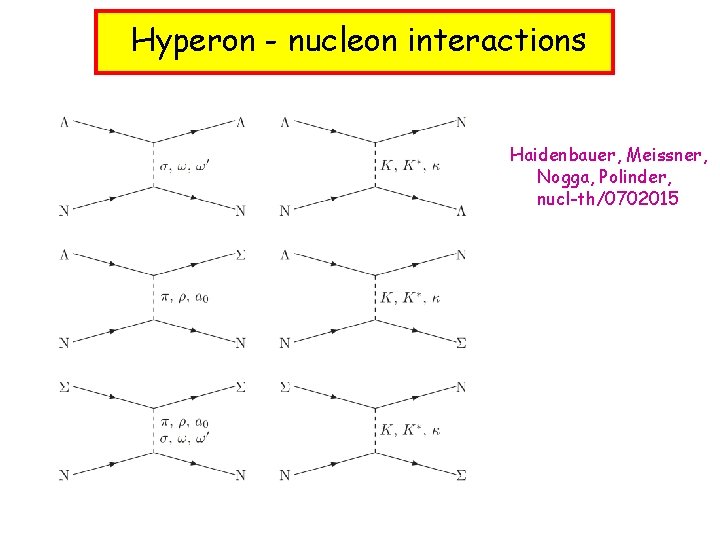
Hyperon - nucleon interactions Haidenbauer, Meissner, Nogga, Polinder, nucl-th/0702015

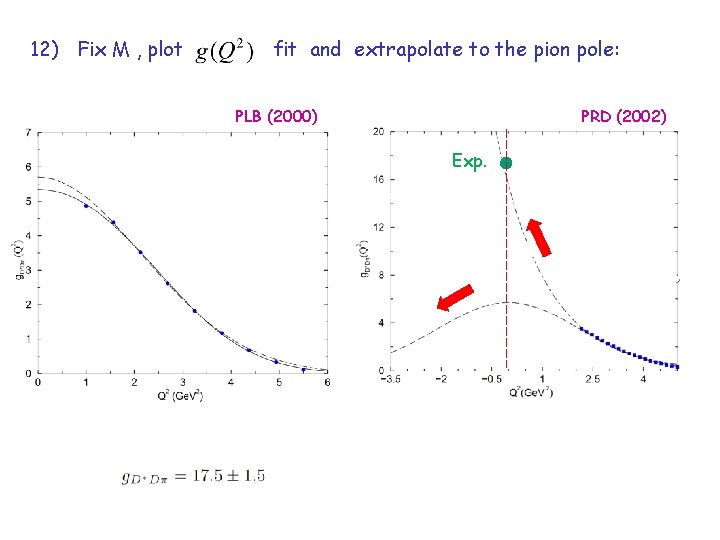
12) Fix M , plot fit and extrapolate to the pion pole: PLB (2000) PRD (2002) Exp.

8) Check the pole dominance: old

É difícil acreditar. . .

But we can estimate the Laplacian : Compute the Lagrangian, energy-momentum tensor and obtain the EOS :