Quadratic Functions and Transformations Standard Form of a

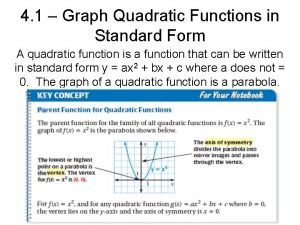
Quadratic Functions and Transformations. Standard Form of a Quadratic Function n r a le l l ’ u o y To identify and graph quadratic functions. at h W To describe and graph transformations of functions. To identify the axis of symmetry, vertex, domain, and range for a given parabola in the vertex form and the standard form of the quadratic function. Voc y r a l abu Parabola, quadratic function, vertex form, axis of symmetry, vertex of the parabola, minimum value maximum value

Take a note A parabola is the graph of a quadratic function, which you can write in the form Remember this is a transformation of the parent function The vertex form of the quadratic function is Translation on the y-axis Reflection, stretch and compression Translation in the x-axis

Go to geogebra qua 2 http: //www. geogebratube. org/student/m 5170 http: //www. geogebratube. org/student/m 6662 http: //www. geogebratube. org/student/m 6452 http: //www. geogebratube. org/student/m 5167 http: //www. geogebratube. org/student/m 9679 http: //www. geogebratube. org/student/m 9511

vertex form a>0 Open upward. The y-coordinate of the vertex is the minimum a‹ 0 Open downward The y-coordinate of the vertex is the maximum value a>1 stretch 0<a‹ 1 compression Vertex (h, k) Axis of symmetry is x=h

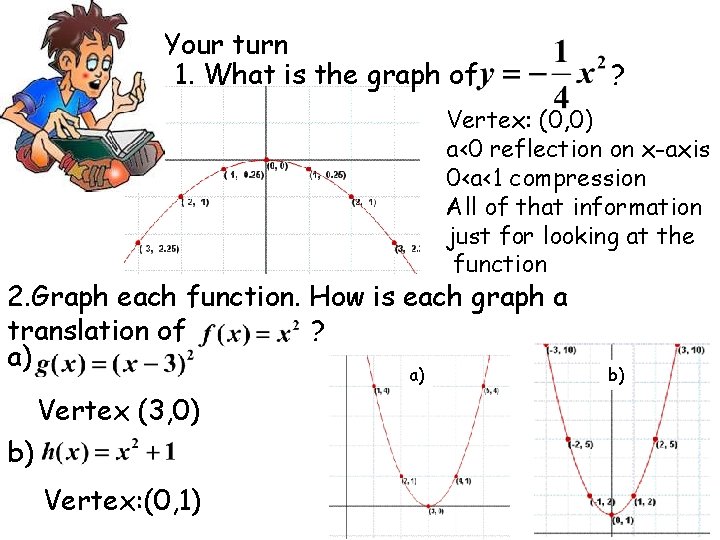
Your turn 1. What is the graph of ? Vertex: (0, 0) a‹ 0 reflection on x-axis 0‹a‹ 1 compression All of that information just for looking at the function 2. Graph each function. How is each graph a translation of ? a) a) Vertex (3, 0) b) Vertex: (0, 1) b)

3. For. What are the vertex, the axis of symmetry, the minimum or maximum value, the domain, and range? Vertex (3, -5) Axis of symmetry x=3 a=1/2 compression Minimum on y=-5 4. The arch of the Sidney Harbor Bridge is approximately 500 meters long and 85 meters high. What quadratic function models the curve of the arch? Assume the arch starts at (0, 0).

Note Standard form Vertex Form vertex (h, k) Axis of symmetry x=h Y-intercept is (0, c) a has the same meaning for both

Converting standard form to vertex form. What is the vertex form of a=2 b=10 c=7 The vertex is (-2. 5, -5. 5) Your turn What is the vertex form of Answer: ?

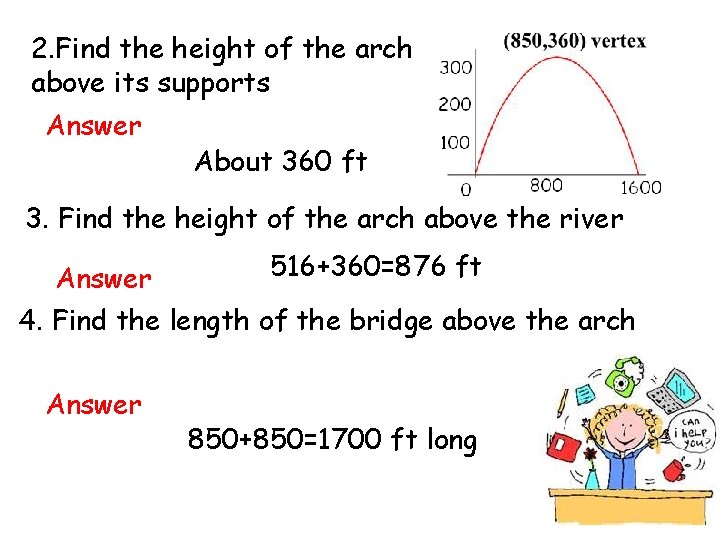
Interpreting a quadratic graph The new River George Bridge in West Virginia is the world’s largest steel single arch bridge. 516 You can model the arc with the function where x and y are in feet. How high above the river is the arch? How long is the section of the bridge above the arch? a=-0. 000498 1. Find the vertex b=0. 847

2. Find the height of the arch above its supports Answer About 360 ft 3. Find the height of the arch above the river 516+360=876 ft Answer 4. Find the length of the bridge above the arch Answer 850+850=1700 ft long

Your turn The Zhaozhou Bridge in China is the oldest known arch bridge, dating to A. D. 605. You can model the support arch with the function Where x and y are measured in feet. How high is the arch above the supports a= - 0. 001075 b= 0. 131148 Answer: 4 ft

Classwork odd Homework even Text book pages 199 -200 exercises 7 -56 Text book pages 206 -207 exercises 8 -47