VERTEX FORM Vertex Form Vertex form is another

VERTEX FORM

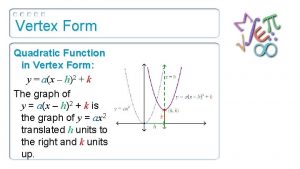
Vertex Form Vertex form is another form for quadratics So far we know Standard form : y = ax² + bx + c Intercept form : y = a(x – s)(x – t) Vertex form is y = a(x – h)² + k Why is vertex form useful?

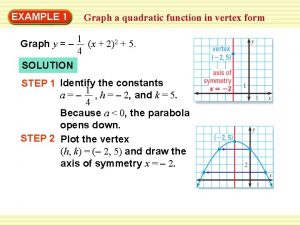
Vertex Form Vertex form is useful when talking about quadratics because it tells us where the vertex is When we are given a quadratic in vertex form, we can find our vertex by looking at (h, k)

y = a(x – h)² + k What is the vertex in the following examples? (h, k) y = (x – 2)² + 1 y = 2(x – 3)² + 4 y = -3(x + 5)² - 1 y = (x + 1)² y=x²-5 y = (x – 4)² + 2 y = 3(4 + x)² + 1 y = -0. 5(x – 2)²

Standard Form to Vertex Form The quadratic equations that we have seen have mostly been in standard form y = ax² + bx + c What if we want our equation in vertex form to make it easier to graph and find the vertex? y = a(x – h)² + k

We have seen already how to change standard form to intercept form to be able to find the zeroes of a solution Today we will learn how to change standard form to vertex form to be able to find the vertex Now we will have a method for finding the zeroes and finding the vertex

Standard Form to Vertex Form We have a method that changes standard form to vertex form that we call completing the square

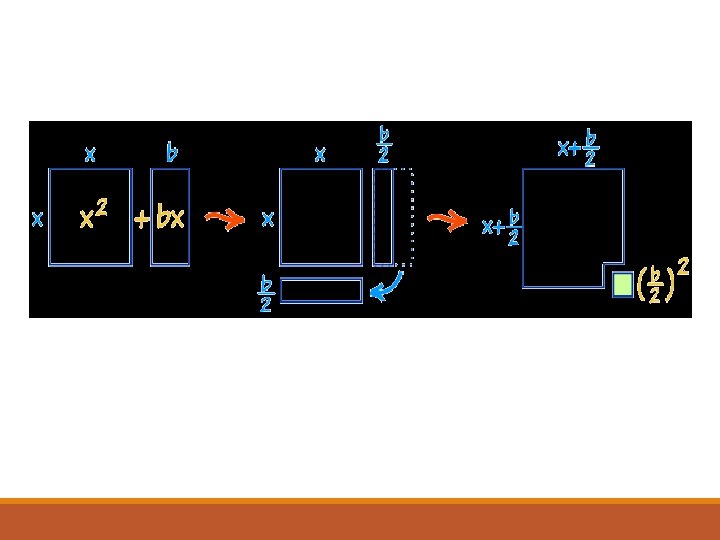
Review Perfect Square Trinomial This means we can factor ax² + bx + c into (a – b)² or (a + b)² For example, if we factor y = x² + 4 x + 4 We get y = (x + 2)² Which is in vertex form with k = 0 y = a(x – h)² + k Let’s look at some more examples

Completing The Square Some quadratic functions can written as a perfect square. x 2 + 8 x + 16 x 2 + 10 x + 25 (x + 4)2 (x + 5)2 Similarly when the coefficient of x is negative: x 2 - 4 x + 4 (x - 2)2 x 2 - 12 x + 36 What is the relationship between the constant term and the coefficient of x? (x - 6)2 The constant term is always (half the coefficient of x)2.

Completing The Square When the coefficient of x is odd we can still write a quadratic expression as a non-perfect square, provided that the constant term is (half the coefficient of x)2 x 2 + 3 x + 2. 25 x 2 + 5 x + 6. 25 (x + 1. 5)2 (x + 2. 5)2 x 2 - 7 x + 12. 25 x 2 - 9 x + 20. 25 (x - 3. 5)2 (x - 4. 5)2

Completing The Square This method enables us to write equivalent expressions for quadratics of the form ax 2 + bx. We simply half the coefficient of x to complete the square then remember to correct for the constant term. x 2 + 4 x = (x + 2)2 - 4 x 2 - 6 x = (x - 3)2 - 9 x 2 + 10 x = (x + 5)2 - 25 x 2 - 12 x = (x - 6)2 - 36

Completing The Square We can also write equivalent expressions for quadratics of the form ax 2 + bx + c. Again, we simply half the coefficient of x to complete the square and remember to take extra care in correcting for the constant term. x 2 + 4 x + 3 x 2 + 10 x + 15 = (x + 2)2 - 1 = (x + 5)2 - 10 x 2 - 2 x + 10 x 2 - 12 x - 1 = (x - 1)2 + 9 = (x - 6)2 - 37

Completing The Square We can also write equivalent expressions for quadratics of the form ax 2 + bx + c. Again, we simply half the coefficient of x to complete the square and remember to take extra care in correcting for the constant term. x 2 + 6 x - 8 x 2 + 2 x + 9 = (x + 3)2 - 17 = (x + 1)2 + 8 Now try these x 2 - 3 x + 2 = (x - 1. 5)2 - 0. 25 x 2 - 5 x - 3 = (x - 2. 5)2 - 9. 25

Completing The Square We can also write equivalent expressions for quadratics of the form ax 2 + bx + c. Again, we simply half the coefficient of x to complete the square and remember to take extra care in correcting for the constant term. Questions: Write the following in completed square form: 1. x 2 + 8 x + 10 = (x + 4)2 - 6 2. x 2 - 6 x + 1 = (x - 3)2 - 8 3. x 2 - 2 x + 2 = (x - 1)2 + 1 4. x 2 + 10 x + 30 = (x + 5)2 + 5 5. x 2 + 6 x - 5 = (x + 3)2 - 14 6. x 2 - 12 x - 3 = (x - 6)2 - 39 7. x 2 - x + 4 = (x - ½)2 + 3. 75 8. x 2 - 3 x + 7. 25 = (x - 1. 5)2 + 5 Questions 1

To complete the square for quadratics where our ‘a’ is a constant other than 1, we simply common factor ‘a’ from ‘a’ and ‘b’. Note that we do not common factor ‘a’ out of term ‘c’ Once ‘a’ is factored out, we complete the square the same way

y = 2 x² - 12 x - 1

Completing the Square Completing the square for quadratic expressions helps us to sketch our graphs accurately with our vertex (h, k) and our ‘a’ value which gives us the direction of opening of our graph as well as how wide or narrow it is compared to y = x²

However, being able to convert between all three forms is very important depending on what we want to use our equation for Recall the three forms are: Standard form – y = ax² + bx + c Vertex form – y = a(x – h)² + k Intercept form – y = a(x – s)(x – t) Let’s do some examples converting between the three forms

Converting Quadratic Equations A STEP-BY-STEP GUIDE WITH PRACTICE

Intercept Form to Standard Form Write the equation in standard form: y = – 2(x + 3)(x – 2)

Intercept Form to Standard Form Write the equation in standard form: y = – 2(x + 3)(x – 2) y = – 2(x 2 + x – 6) multiply binomials If you need a hint …go to next slide to see next step.

Intercept Form to Standard Form Write the equation in standard form: y = – 2(x + 3)(x – 2) y = – 2(x 2 + x – 6) y = – 2 x 2 – 2 x + 12 multiply binomials distribute

Intercept Form to Standard Form Try these: y = 3(x + 1)(x + 2) y = ½ (2 x + 3)(x – 2)

Intercept Form to Standard Form Try these: y = 3(x + 1)(x + 2) y = 3 x 2 + 9 x + 6 y = ½ (2 x + 3)(x – 2) y = x 2 –½x– 3

Vertex Form to Standard Form Write this equation in standard form: y = 2(x – 3)2 + 4

Vertex Form to Standard Form Write this equation in standard form: y = 2(x – 3)2 + 4 y = 2(x 2 – 6 x + 9) + 4 square the binomial

Vertex Form to Standard Form Write this equation in standard form: y = 2(x – 3)2 + 4 y = 2(x 2 – 6 x + 9) + 4 square the binomial y = 2 x 2 – 12 x + 18 + 4 distribute

Vertex Form to Standard Form Write this equation in standard form: y = 2(x – 3)2 + 4 y = 2(x 2 – 6 x + 9) + 4 square the binomial y = 2 x 2 – 12 x + 18 + 4 distribute y = 2 x 2 – 12 x + 22 combine like terms

Vertex Form to Standard Form Try these: y = 3(x + 1)2 – 5 y = – (x + 3)2 – 2

Standard Form to Intercept Form Write the equation in intercept form: y = – 15 x 2 + 3 x + 12

Standard Form to Intercept Form Write the equation in intercept form: y = – 15 x 2 + 3 x + 12 y = – 3(5 x 2 – x – 4) common factor y = – 3(5 x + 4)(x – 1) factor the trinomial

Standard Form to Intercept Form Try these: y = x 2 – 12 x + 32 y = 5 x 2 – 25 x + 30 Check your answers on the next slide.

Standard Form to Intercept Form Try these: y = x 2 – 12 x + 32 y = (x – 8)(x – 4) y = 5 x 2 – 25 x + 30 y = 5(x – 2)(x – 3)

Standard Form to Vertex Form Write the equation in vertex form: y = 3 x 2 – 6 x + 8 If you need a hint …go to next slide to see next step.

Standard Form to Vertex Form Write the equation in vertex form: y = 3 x 2 – 6 x + 8 y = 3(x 2 – 2 x ) + 8 factor out “a” If you need a hint …go to next slide to see next step.

Standard Form to Vertex Form Write the equation in vertex form: y = 3 x 2 – 6 x + 8 y = 3(x 2 – 2 x ) + 8 factor out “a” y = 3(x 2 – 2 x + 1) + 8 – 3 complete the square If you need a hint …go to next slide to see next step.

Standard Form to Vertex Form Write the equation in vertex form: y = 3 x 2 – 6 x + 8 y = 3(x 2 – 2 x ) + 8 factor out “a” y = 3(x 2 – 2 x + 1) + 8 – 3 complete the square y = 3(x – 1)2 + 5 factor and combine

Standard Form to Vertex Form Try these: y = x 2 – 4 x + 10 y = – 2 x 2 – 4 x + 1 Check your answers on the next slide.

Standard Form to Vertex Form Try these: y = x 2 – 4 x + 10 y = (x – 2)2 + 6 y = – 2 x 2 – 4 x + 1 y = – 2(x + 1)2 + 3

More Practice Write this equation in intercept form: y = (x + 4)2 – 1 Write this equation in vertex form: y = (x – 3)(x + 1) Check your answers on the next slide.

More Practice Write this equation in intercept form: y = (x + 4)2 – 1 y = (x + 5)(x + 3) Write this equation in vertex form: y = (x – 3)(x + 1) y = (x – 1)2 + 1