Quadratics Parts of a Parabola and Vertex Form

Quadratics Parts of a Parabola and Vertex Form

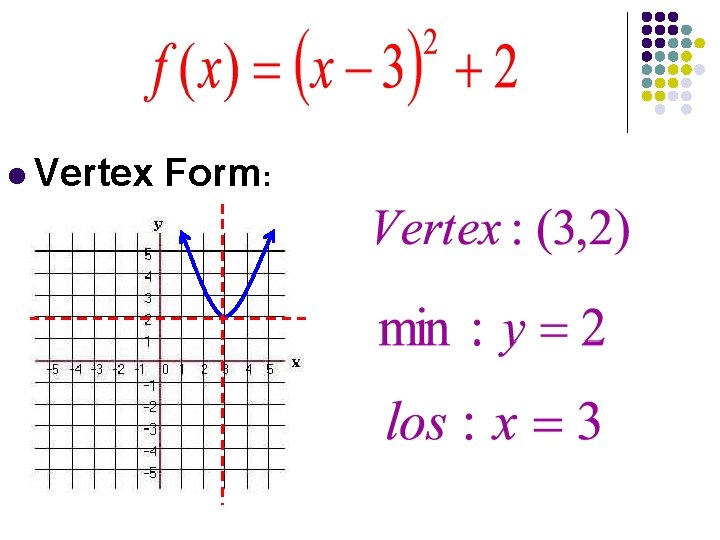
Quadratic Functions l Function: l Standard Form (Vertex Form): l Graphs a parabola l All are symmetric to a line called the axis of symmetry or line of symmetry (los)

Show that g represents a quadratic function. Identify a, b, and c.

Show that g represents a quadratic function. Identify a, b, and c.

Show that g represents a quadratic function. Identify a, b, and c.

Parts of a Parabola l Axis of Symmetry (Line of Symmetry) LOS: The line that divides the parabola into two parts that are mirror images of each other. l Vertex: Either the lowest or highest point.

Let’s look at a transformation What is the vertex, max or min, and los?

l Vertex Form:

Let’s look at a transformation What is the vertex, max or min, and los?

l Vertex Form:

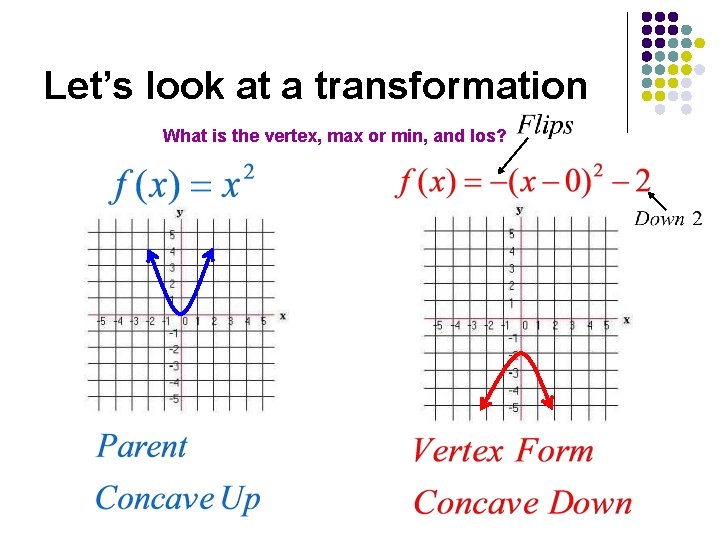
Let’s look at a transformation What is the vertex, max or min, and los?

l Vertex Form:

Finding the Vertex and los on the GDC l l l Put equation into y 1. Press Zoom 6 – fix if necessary by changing the window. Press 2 nd Trace (Calc). Press max/min. Left of it; Then right of it; Then ENTER.

Let’s Try It…. l Find the vertex, min, and los.

Use your GDC to find the zeros (x-intercepts)…. l l l Press 2 nd Trace (Calc) Press zero. Again, to the left, to the right, ENTER.

Find the zeros for the last example.

Example: l Find the vertex, los, max/min, zeros, and tell whether concave up or concave down.

Example: l Find the vertex, los, max/min, zeros, and tell whether concave up or concave down. These are the solutions. What are the x-intercepts?

Example: l Find the vertex, los, max/min, zeros, and tell whether concave up or concave down. These are the solutions. What are the x-intercepts?

Example l Find the vertex, los, max/min, zeros, and tell whether concave up or concave down.

Example: l Find the vertex, los, max/min, zeros, and tell whether concave up or concave down.

Example: l Find the vertex, los, max/min, zeros, and tell whether concave up or concave down.

How do I know if it is concave up or down just by looking at the function? l In the following examples, state whether the parabola is concave up or down and whether the vertex is a max or a min by just looking at the function.

Write the equation in standard form of the parabola whose vertex is (1, 2) and passes through the point (3, -6). (h, k) (x, y)

Write the equation in standard form of the parabola whose vertex is (-2, -1) and (h, k) passes through the point (0, 3). (x, y)

Write the equation in standard form of the parabola whose vertex is (4, -1) and passes (h, k) through the point (2, 3). (x, y)

A golf ball is hit from the ground. Its height in feet above the ground is modeled by the function where t represents the time in seconds after the ball is hit. How long is the ball in the air? Graph on GDC. Find the zeros. Answer: 11. 25 seconds What is the maximum height of the ball? Graph on GDC. Find the maximum y-value. Answer: 506. 25 feet

l A. What is the maximum height of the ball? Graph and find the maximum y-value. Answer: 21 feet B. At what time does the ball reach its maximum height? Set equation = to 21 and find the zeros. Answer: 1 second C. At what time(s) is the ball 16 feet high in the air? Set equation = to 16 and find the zeros. Answer: 1. 56 seconds and 0. 44 seconds.

§ . A. What ticket price gives the maximum profit? Graph and find the maximum x-value. Hint: Press Zoom 0 and change x-max to 50 and y max to 8000. Answer: $25 B. What is the maximum profit? Graph and find the maximum y-value. Hint: Press Zoom 0 and change x-max to 50 and y max to 8000. Answer: $6, 000 C. What ticket price would generate a profit of $5424? Set equation = to 5424 and find the zeros. Hint: Press zoom 0. Answer: $19 or $31