Vertex Form Quadratic Function in Vertex Form y

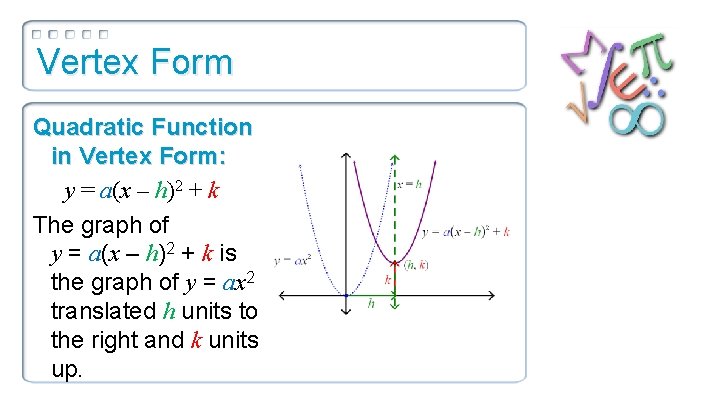
Vertex Form Quadratic Function in Vertex Form: y = a(x – h)2 + k The graph of y = a(x – h)2 + k is the graph of y = ax 2 translated h units to the right and k units up.

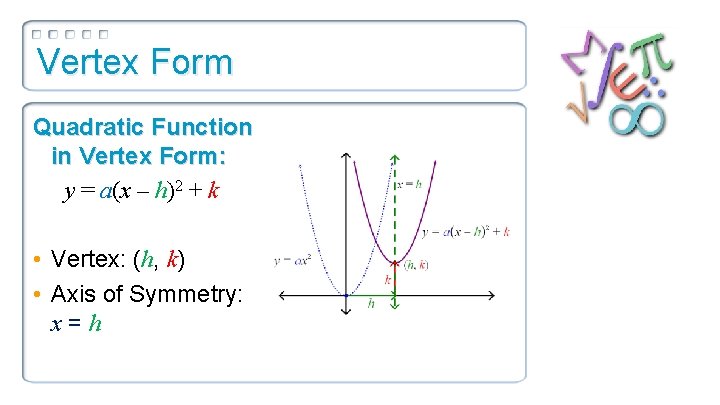
Vertex Form Quadratic Function in Vertex Form: y = a(x – h)2 + k • Vertex: (h, k) • Axis of Symmetry: x=h

Exercise 1 What is the y-intercept of the graph of y = a(x – h)2 + k?

Exercise 2 What are the x-intercepts of the graph of y = a(x – h)2 + k?

Graphing Quadratic Functions, II To graph y = a(x – h)2 + k use SRT transformations. • Scaling: a times the y-coordinate • Reflecting: over the x-axis if a < 0 • Translating: Left/Right h units and Up/Down k units – Remember that the up/down movement is in the direction of the sign of k, but for left/right, it’s the opposite direction as the sign of h.

Exercise 3 Graph

Exercise 4 Graph

Objective 1 b You will be able to graph a quadratic function in intercept form

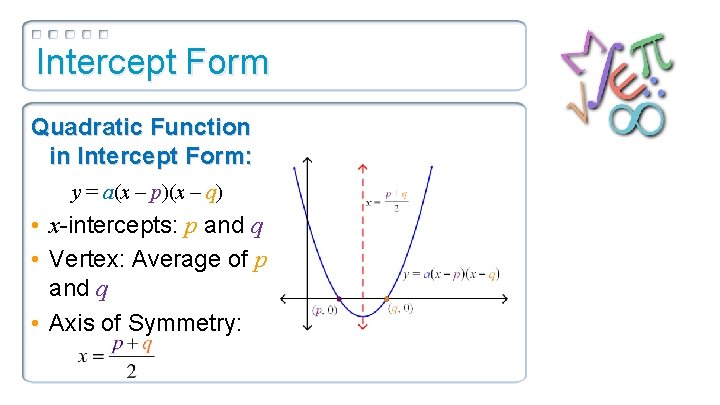
Intercept Form Quadratic Function in Intercept Form: y = a(x – p)(x – q) • x-intercepts: p and q • Vertex: Average of p and q • Axis of Symmetry:

Exercise 5 What is the y-intercept of the graph of y = a(x – p)(x – q)?

Graphing Quadratic Functions, III To graph y = a(x – p)(x – q): 1. Use the a-value to determine or 2. Plot the x-intercepts p and q 3. Find and plot the vertex (x = average of p and q) 4. Graph the axis of symmetry 5. Find and plot a couple of other function values and their reflections

Exercise 6 Graph

Exercise 7 Graph

You will be able to rewrite your quadratic function in standard, vertex, or intercept form Objective 2

Exercise 8 a Write each function in standard form. 1. 2.

Protip #1: Standard Form To write your quadratic equation in standard form is really easy. Just FOIL, distribute, or expand as necessary, and then combine like terms. Finally, make it look like this: y = ax 2 + bx + c

Exercise 8 b Write each function in standard form. 1. 2.

Exercise 9 a Write each function in intercept form. 1. 2.

Protip #2: Intercept Form To write your equation in intercept form, you have to do some factoring: 1. Factor out GCF. That includes a − 1 if the leading term is negative 2. Factor the trinomial that is left over

Protip #2: Intercept Form To write your equation in intercept form, you have to do some factoring: 3. Each factor has to look like (x ± p). This means you have to divide out any coefficient of x from each factor. Whatever you divide out becomes part of the a-value. Divide out a 2 Divide out a 3

Protip #2: Intercept Form To write your equation in intercept form, you have to do some factoring: 3. Each factor has to look like (x ± p). This means you have to divide out any coefficient of x from each factor. Whatever you divide out becomes part of the a-value.

Exercise 9 b Write each function in intercept form. 1. 2.

Exercise 10 a Write each function in vertex form. 1. 2.

Protip #3: Vertex Form To put a quadratic equation in vertex form, you have to complete the square on only one side of the equation. 1. Separate the constant term from the variable terms 2. Factor out the leading coefficient from the variable terms

Protip #3: Vertex Form To put a quadratic equation in vertex form, you have to complete the square on only one side of the equation. 3. Complete the square with the variable terms 4. Whatever you add on the inside of the parenthesis, subtract on the outside of the parenthesis. 9 36

Protip #3: Vertex Form 5. Remember that what you add on the inside of the parenthesis is actually multiplied by the leading coefficient that you factored out in Step 2. Make sure to multiply by this number before subtracting on the outside of the parenthesis 9 36

Exercise 10 b Write each function in vertex form. 1. 2.

Solving Quadratic Equations Objectives: 1. To solve a quadratic equation by factoring

Warm-Up • Zero Product Property If the product of two expressions is zero, then at least of the expressions equal zero. Maybe that’s zero Or maybe this one’s zero (Or maybe they’re both zero)

Vocabulary Parabola Zeros (of a function) Roots (of a function)

Objective 1 You will be able to solve a quadratic equation by factoring

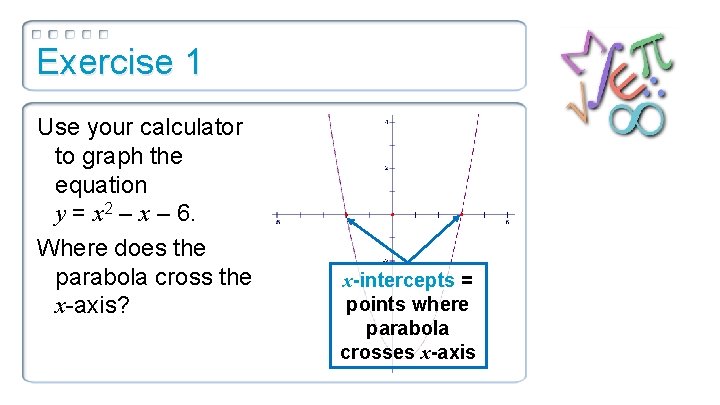
Exercise 1 Use your calculator to graph the equation y = x 2 – x – 6. Where does the parabola cross the x-axis? x-intercepts = points where parabola crosses x-axis

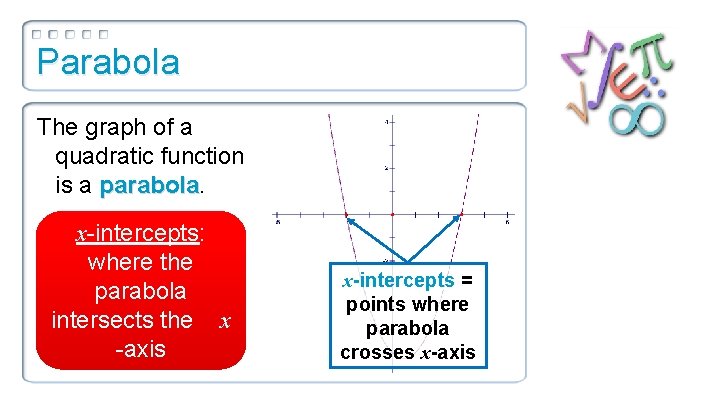
Parabola The graph of a quadratic function is a parabola x-intercepts: where the parabola intersects the x -axis x-intercepts = points where parabola crosses x-axis

Exercise 2 How many y-intercepts can the graph of the quadratic function y = ax 2 + bx + c have? – Only one since it’s a function! How many x-intercepts can the graph of the quadratic function y = ax 2 + bx + c have? – Two, one, or none!

Exercise 3 If you wanted to find the y-intercept of a quadratic function, what would you do? Plug in zero for x and solve for y

Exercise 4 Find the y-intercept of y = x 2 – 6 x – 7.

Exercise 5 If you wanted to find the x-intercept of a quadratic function, what would you do? Plug in zero for y and solve for x

Exercise 6 Find the x-intercept(s) of y = x 2 – 6 x – 7. The problem here is, how do you solve 0 = x 2 – 6 x – 7 since you can’t just get x by itself? The answer is to use the Zero Product Property

Solving Quadratic Equations The standard form of a quadratic equation in one variable is ax 2 + bx + c = 0, where a is not zero. Solving a quadratic equation in standard form is the same thing as finding the x-intercepts of y = ax 2 + bx + c.

Solving Quadratic Equations The standard form of a quadratic equation in one variable is ax 2 + bx + c = 0, where a is not zero. We can use the zero product property to solve certain quadratic equations in standard form if we can write ax 2 + bx + c as a product of two expressions. To do that, we have to factor!

Exercise 7 Find the x-intercept(s) of y = x 2 – 6 x – 7. Let y = 0 Factor Set each factor equal to zero x-intercepts: (7, 0) and (− 1, 0)

Solving Quadratic Equations To solve a quadratic equation, try applying the zero product property. Factor your 1 Step quadratic Set each factor equal to Step 2 zero and solve

Exercise 8 Solve 0 = x 2 – x – 42.

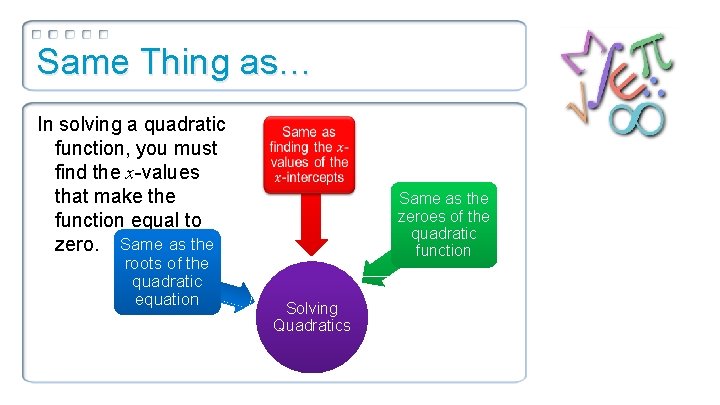
Same Thing as… In solving a quadratic function, you must find the x-values that make the function equal to zero. Same as the roots of the quadratic equation Same as the zeroes of the quadratic function Solving Quadratics

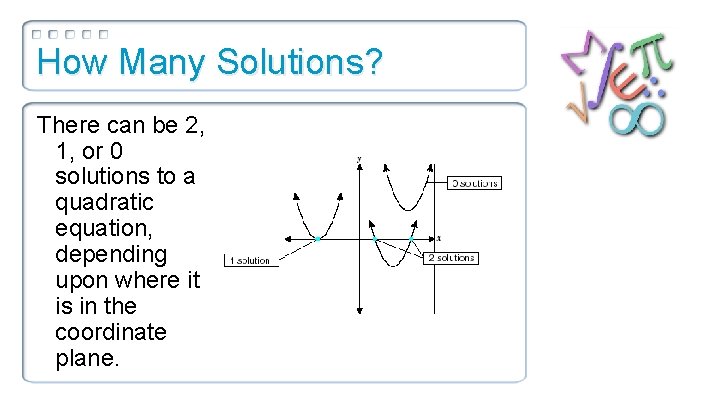
How Many Solutions? There can be 2, 1, or 0 solutions to a quadratic equation, depending upon where it is in the coordinate plane.

Exercise 9 Find the roots of each equation. 1. x 2 + 2 x = 0 2. x 2 – 12 x +36 = 0 3. x 2 + 1 = 0 4. x 2 + 2 x + 4 = 0

Exercise 10 Explain why you cannot use the zero product property to solve every quadratic equation.

Exercise 11 Find the zeros of each function. 1. y = 16 x 2 – 4 2. y = 9 x 2 + 12 x + 4 3. y = 5 x 2 + 16 x + 3 4. y = 2 x 2 + x + 3

Exercise 12 Solve the equation. 1. 4 x 2 – 17 x – 15 = 0 2. 3 x 2 + 22 x + 60 = -14 x – 48

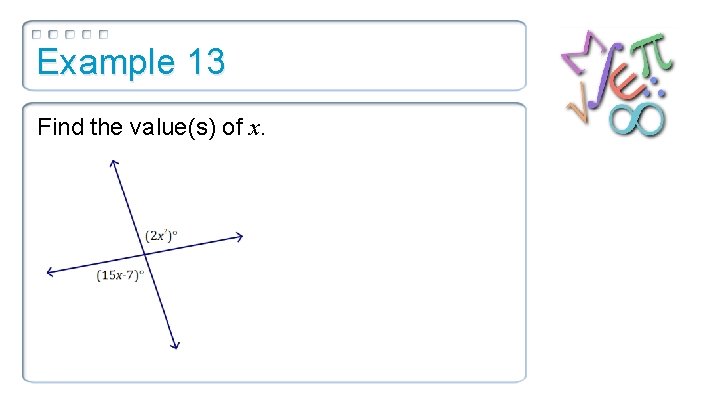
Example 13 Find the value(s) of x.

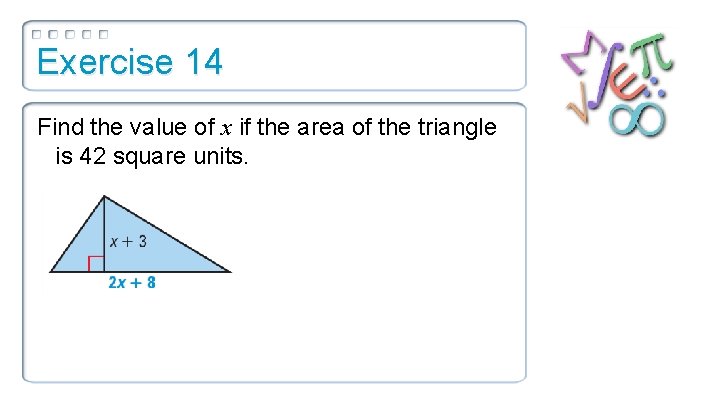
Exercise 14 Find the value of x if the area of the triangle is 42 square units.

Exercise 15 Use substitution to solve the system of equations.

Solving Quadratic Equations Objectives: 1. To solve a quadratic equation by factoring

Warm-Up Solve for x. x 2 – 10 x + 25 = 35

Perfect Squares? The previous exercise was an interesting example, but not every trinomial is a perfect square trinomial. However, we can cleverly rearrange the terms to make any trinomial into a perfect square. This is called completing the square

Objective 1 You will be able to solve quadratic functions by completing the square

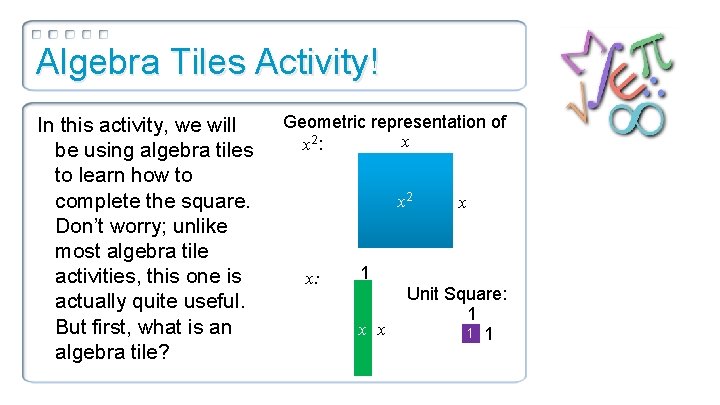
Algebra Tiles Activity! In this activity, we will be using algebra tiles to learn how to complete the square. Don’t worry; unlike most algebra tile activities, this one is actually quite useful. But first, what is an algebra tile? Geometric representation of x x 2: x 2 x: x 1 x x Unit Square: 1 1 1

Algebra Tiles Activity! 1. You’ll need some tiles, so cut them out. 2. Use your tiles to represent x 2 + 6 x. x 2 x x x 3. What you want to accomplish is to make your polynomial model into a square by rearranging your tiles and adding the correct number of unit squares.

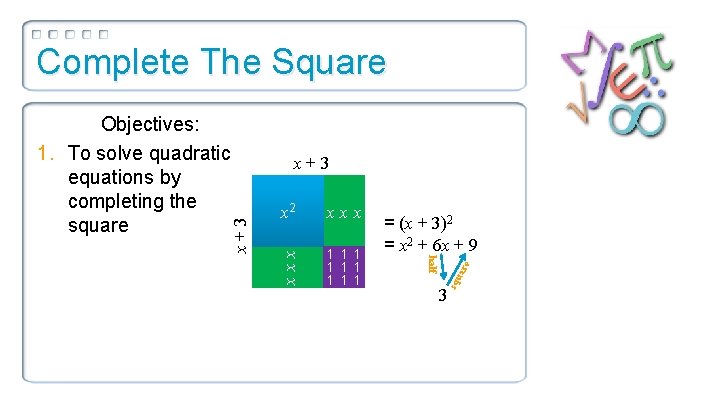
Algebra Tiles Activity! x 2 xxx x+3 1 1 1 1 1 To create this square, put half of your x’s on one side of the square and the 2 = (x + 3) other half of your = x 2 + 6 x + 9 x’s on the other side of the square. Now fill in the missing bits with unit squares.

Algebra Tiles Activity! 4. Now, let’s try again, this time 5. Based on your with the following expressions. investigation, how could you complete the square given x 2 + bx?

Algebra Tiles Activity! 1 1 1 1 1 = (x + 3)2 = x 2 + 6 x + 9 squ are xxx half x 2 xxx x+3 3 In general then, to complete the square, you take half of the middle term and then square it. The number you get becomes the constant term.

Algebra Tiles Activity! 1 1 1 1 1 squ are xxx half x 2 xxx x+3 Notice also that the number you get from taking half of the middle term = (x + 3)2 becomes the = x 2 + 6 x + 9 constant of the 3 binomial that gets squared.

Completing The Square

Exercise 1 a Find the value of c that makes x 2 – 26 x + c a perfect square trinomial. The write the expression as the square of a binomial.

Exercise 1 b Find the value of c that makes x 2 + 7 x + c a perfect square trinomial. The write the expression as the square of a binomial.

Exercise 1 c Find the value of c that the expression a perfect square trinomial. The write the expression as the square of a binomial. 1. x 2 + 14 x + c 2. x 2 – 22 x + c 3. x 2 – 9 x + c

Exercise 2 Solve by finding square roots. 1. x 2 + 6 x + 9 = 36 2. x 2 – 10 x + 25 = 1

Solving Quadratics Completing the square allows you to solve almost any quadratic equation, regardless of whether it is a perfect square. This is basically an application of the Addition Property of Equality.

Solving Quadratics Solving a Quadratic Equation by Completing the Square: 1. Use addition/subtraction to write your equation in the form x 2 + bx = c. 2. Complete the square on the quadratic side of the equation and add this number to both sides of the equation. 3. Factor and take the square root.

Exercise 3 a Solve 3 x 2 – 36 x +150 = 0 by completing the square.

Exercise 3 b Solve the equation by completing the square. 1. x 2 + 6 x + 4 = 0 2. x 2 – 10 x + 8 = 0 3. 2 x 2 – 4 x – 14 = 0 4. 3 x 2 + 12 x – 18 = 0

Exercise 4 a Solve x 2 – 9 x + 20 = 0 by completing the square.

Exercise 4 b Solve the equation by completing the square. 1. x 2 + 3 x − 5 = 0 2. x 2 – 7 x + 13 = 0

Exercise 5 a Solve 2 x 2 – 12 x + 7 = 0 by completing the square.

Exercise 5 b Solve the equation by completing the square. 1. 3 x 2 + 24 x + 41 = 0 2. x 2 – x + 6 = 0

Complete The Square x+3 1 1 1 1 1 = (x + 3)2 = x 2 + 6 x + 9 squ are xxx half x 2 xxx x+3 Objectives: 1. To solve quadratic equations by completing the square 3

Vocabulary Real Number Complex Number Imaginary Unit Imaginary Number Pure Imaginary Number Absolute Value Complex Plane Complex Conjugates

Objective 1 You will be able to simplify square roots of negative numbers

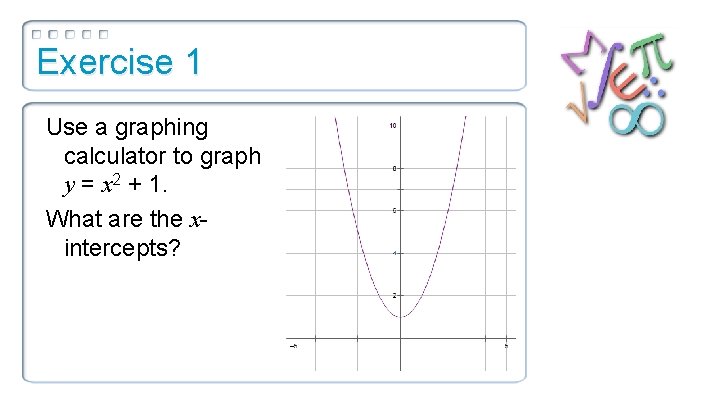
Exercise 1 Use a graphing calculator to graph y = x 2 + 1. What are the xintercepts?

Exercise 2 •

Imaginary Unit •

Exercise 3 A pattern exists as a result of raising i, an imaginary number, to n, an integer greater than or equal to 1. According to the table, what is the value of i raised to the 16 th power? in Solution i 1 i 2 − 1 i 3 i 4 1 i 5 i 6 − 1

Taking Powers of i As the previous example shows, there are only 4 possible values for in. All other powers of 4 just repeat this pattern. So, how do you think you would evaluate i 101?

Taking Powers of i As the previous example shows, there are only 4 possible values for in. Divide the exponent by 4, then use the remainder to find the result: Remainder Result 1 i 2 − 1 3 −i 0 1

Exercise 4 Evaluate each of the following. 1. i 54 2. i 120 3. i 89 4. i 39

Protip: Divisible by 4 How can you tell if a number is divisible by 4? Any multiple of 100 is divisible by 4. Since this is an integer with no remainder, any multiple of 100 is divisible by 4.

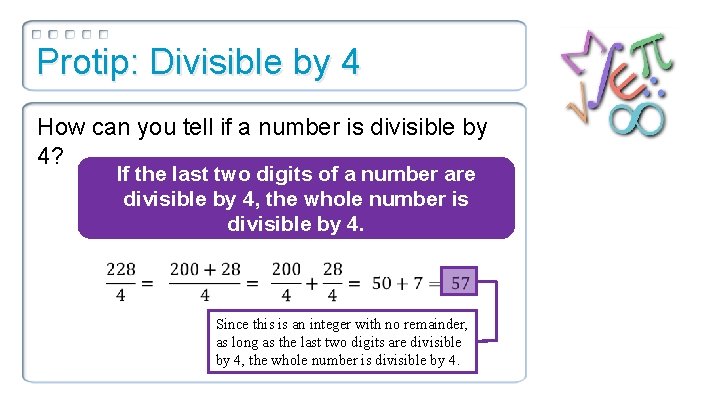
Protip: Divisible by 4 How can you tell if a number is divisible by 4? If the last two digits of a number are divisible by 4, the whole number is divisible by 4. Since this is an integer with no remainder, as long as the last two digits are divisible by 4, the whole number is divisible by 4.

Protip: Divisible by 4 How can you tell if a number is divisible by 4? If the last two digits of a number are divisible by 4, the whole number is divisible by 4. Since this is an integer with no remainder, as long as the last two digits are divisible by 4, the whole number is divisible by 4.

Protip: Divisible by 4 How can you tell if a number is divisible by 4? If the last two digits of a number are divisible by 4, the whole number is divisible by 4. Since this is an integer with no remainder, as long as the last two digits are divisible by 4, the whole number is divisible by 4.

Exercise 5 •

Negative Square Roots The Square Root of a Negative Number Property Example

Exercise 6 a Find the roots of each quadratic equation. 1. x 2 + 1 = 0 2. 2 x 2 + 18 = − 72

Exercise 6 b Solve each equation. 1. x 2 = − 13 2. x 2 + 11 = 3 3. 3 x 2 – 7 = − 31 4. 5 x 2 + 33 = 3

Objective 2 You will be able to plot complex numbers in the complex plane and find their absolute value

Complex Numbers A complex number in standard form is written Real Part Imaginary Part • All real numbers are complex numbers – This happens when b = 0 • For imaginary numbers, numbers b ≠ 0. • For a pure imaginary number, number a = 0.

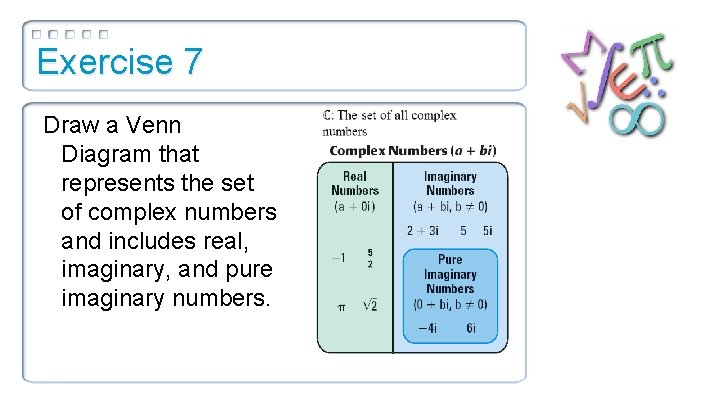
Exercise 7 Draw a Venn Diagram that represents the set of complex numbers and includes real, imaginary, and pure imaginary numbers.

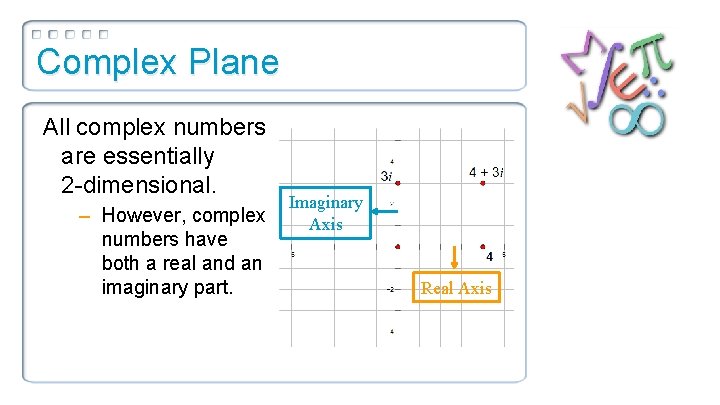
Complex Plane All complex numbers are essentially 2 -dimensional. – When you graph a real number, it appears on a 1 -D number line

Complex Plane All complex numbers are essentially 2 -dimensional. – However, complex numbers have both a real and an imaginary part. Imaginary Axis Real Axis

Exercise 8 Plot the complex numbers on the same complex plane. 1. 4 + 2 i 2. − 1 + 3 i 3. − 4 i 4. 2 – 2 i

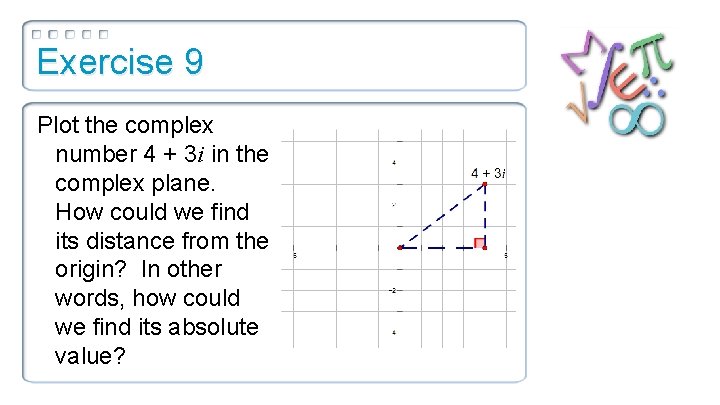
Exercise 9 Plot the complex number 4 + 3 i in the complex plane. How could we find its distance from the origin? In other words, how could we find its absolute value?

Absolute Value of a Complex Number The absolute value of a complex number z = a + bi, denoted |z|, is a nonnegative real number defined as

Exercise 10 a Find the absolute value of each complex number. 1. 5 – 12 i 2. 17 i

Exercise 10 a Find the absolute value of each complex number. 1. 4 – i 2. − 3 – 4 i 3. 2 + 5 i 4. − 4 i

Objective 3 You will be able to add, subtract, multiply, and divide complex numbers

Adding and Subtracting To add or subtract two complex numbers, simply add or subtract their real and imaginary parts separately. Sum (a + bi) + (c + di) = (a + c) + (b + d)i Difference (a + bi) – (c + di) = (a – c) + (b – d)i

Exercise 11 a Write the expression as a complex number in standard form. 1. (12 – 11 i) + (-8 + 3 i) 2. (15 – 9 i) – (24 – 9 i) 3. 35 – (13 + 4 i) + i

Exercise 11 b Write the expression as a complex number in standard form. 1. (9 – i) + (− 6 + 7 i) 2. (3 + 7 i) – (8 – 2 i) 3. − 4 – (1 + i) – (5 + 9 i)

Multiplying To multiply complex numbers, you have to use a combination of the distributive property and properties of the imaginary unit.

Exercise 12 a Write the expression as a complex number in standard from. 1. − 5 i(8 – 9 i) 2. (-8 + 2 i)(4 – 7 i)

Exercise 12 b Write the expression as a complex number in standard from. 1. i(9 – i) 2. (3 + i)(5 – i)

Exercise 13 Multiply and classify the product. 1. (5 i)(− 5 i) 2. (3 + 6 i)(3 – 6 i)

Dividing To “divide” complex numbers, you have to multiply by a complex conjugate The complex numbers a + bi and a – bi are complex conjugates The product of complex conjugates is always a real number

Dividing To “divide” complex numbers, you have to multiply by a complex conjugate The complex numbers a + bi and a – bi are complex conjugates The product of complex conjugates is always a real number

Exercise 14 a Write the quotient in standard form.

Exercise 14 b Write each quotient in standard form. 1. 2.