Different forms of CURVES CARTESIAN FORM POLAR FORM

Different forms of CURVES • CARTESIAN FORM: • POLAR FORM: • PARAMETRIC FORM: • PEDAL FORM: • INTRINSIC FORM: 12/3/2020 Prepared by Dr. C. Mitra 2

12/3/2020 Prepared by Dr. C. Mitra 3

SOAP Symmetry: • About X axis : Every where in the equation powers of y are even. • About Y axis : Every where in the equation powers of x are even. • In opposite quadrants or with respect to origin : On replacing x by –x and y by -y in the equation of the curve, no change in the equation. • About the line y = x : Replace x by y and y by x no change in the equation. 12/3/2020 Prepared by Dr. C. Mitra 4

SOAP Origin: • If the independent constant term is absent in the equation of the curve then it passes through the origin. i. e. if x=0 and y=0 satisfies the equation of the curve then it passes through the origin. • If the curve passes through the origin, then the Tangents to the curve at origin can be obtain by equating to zero lowest degree term of the equation. 12/3/2020 Prepared by Dr. C. Mitra 5

SOAP Asymptote: • A tangent to the curve at infinity is called its asymptote. • Asymptote can be classified into two category – Parallel to X-axis or parallel to Y-axis. – Oblique Asymptote: Neither Parallel to Xaxis nor parallel to Y-axis. 12/3/2020 Prepared by Dr. C. Mitra 6

1. Asymptote parallel to Y-axis • Asymptote Parallel to Y-axis can be obtained by equating to zero the coefficient of highest degree term in y. 2. Asymptote parallel to X-axis • Asymptote Parallel to X-axis can be obtained by equating to zero the coefficient of highest degree term in x. 12/3/2020 Prepared by Dr. C. Mitra 7

3. Oblique Asymptote: • If the Equation of the curve is in the implicit form i. e. f(x, y) = 0, then it may have oblique asymptote. • Procedure: Let y = mx + c be the asymptote. • Solving f(x, mx+c) = 0 and equating the co-efficients of highest and second highest power of x to 0 we get required values of m and c. 12/3/2020 Prepared by Dr. C. Mitra 8

SOAP POINTS • • Find X-Intercept Or Y-Intercept: X-Intercept can be obtained by putting y = 0 in the equation of curve. Y-Intercept can be obtained by putting x = 0 in the equation of curve. For the Curves , 12/3/2020 Prepared by Dr. C. Mitra 9

• If =0, then tangent will be parallel to Xaxis. • If = , then tangent will be parallel to Yaxis. • If > 0, in the Interval a < x < b, then y is increasing function in a < x < b. • If < 0, in the Interval a < x < b, then y is decreasing function in a < x < b. 12/3/2020 Prepared by Dr. C. Mitra 10

Region of Absence: • If y 2<0, for x < a (x=a is an X-intercept), then there is no curve to the left of the line x=a. • If y 2<0, for a < x < b (a and b are Xintercepts) then there is no curve between the lines x = a and x = b. • If y 2<0, for x > b ( x = b is an X-intercept) then there is no curve to the right of the line x=b. 12/3/2020 Prepared by Dr. C. Mitra 11

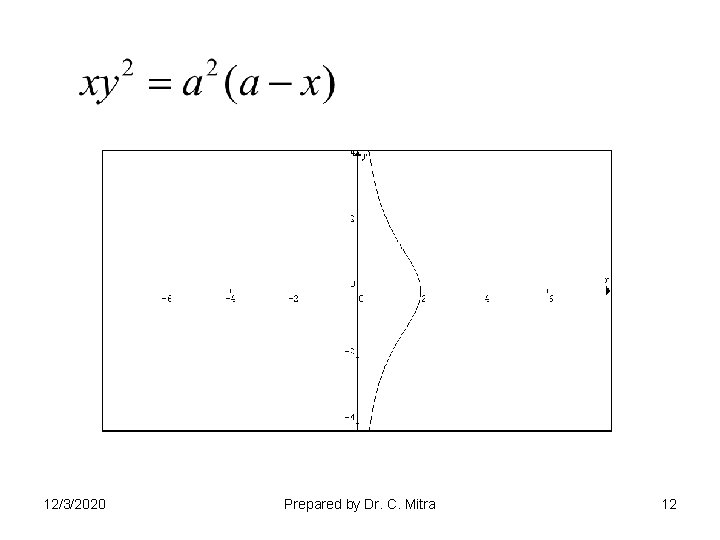
12/3/2020 Prepared by Dr. C. Mitra 12

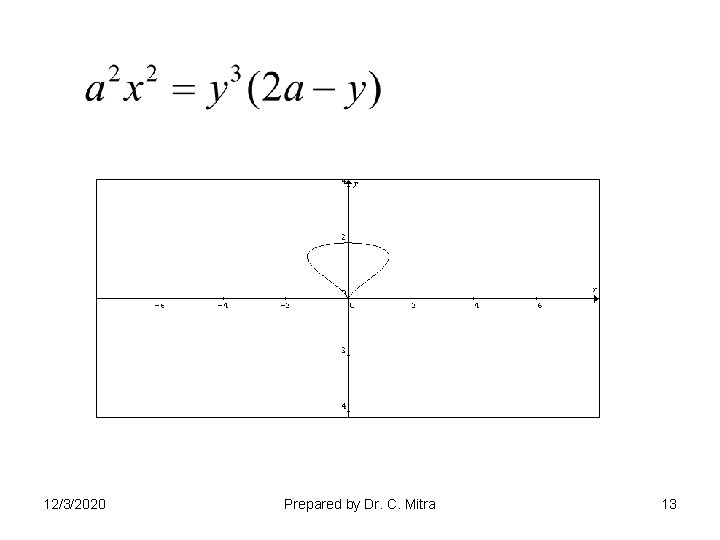
12/3/2020 Prepared by Dr. C. Mitra 13

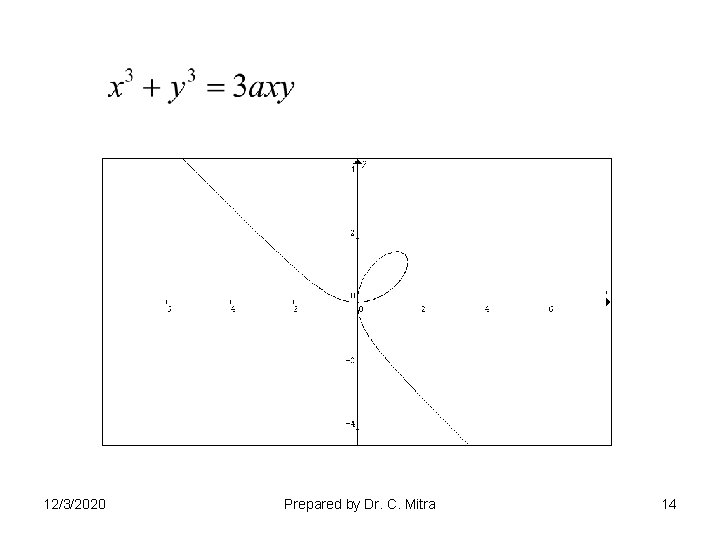
12/3/2020 Prepared by Dr. C. Mitra 14

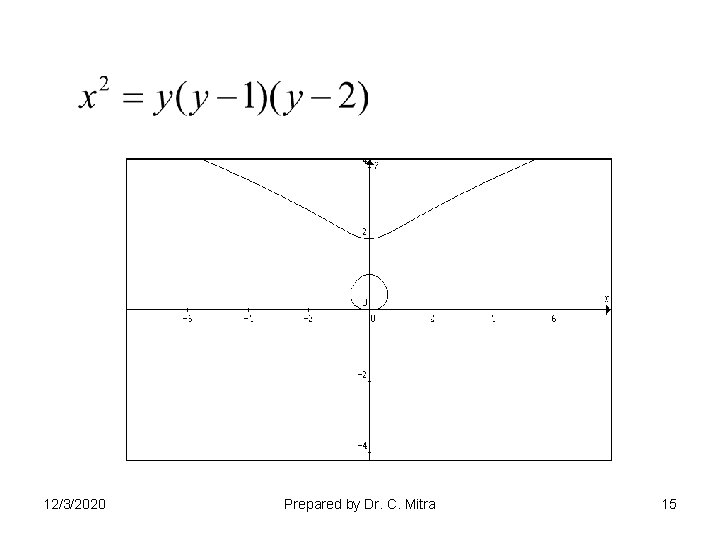
12/3/2020 Prepared by Dr. C. Mitra 15

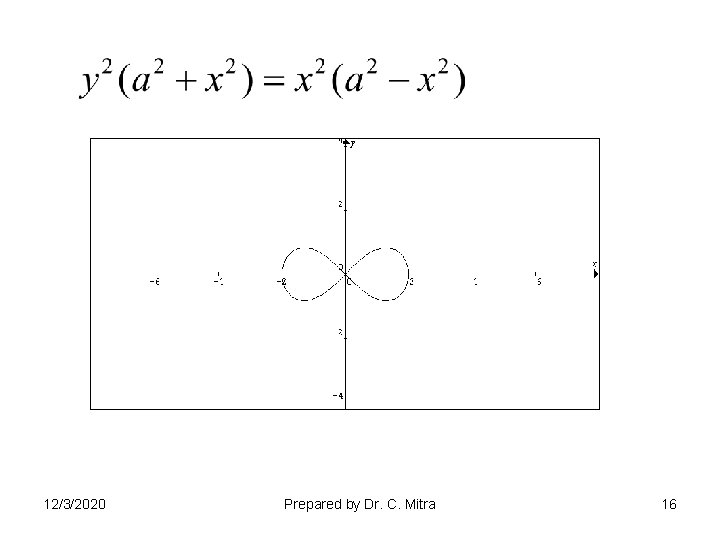
12/3/2020 Prepared by Dr. C. Mitra 16

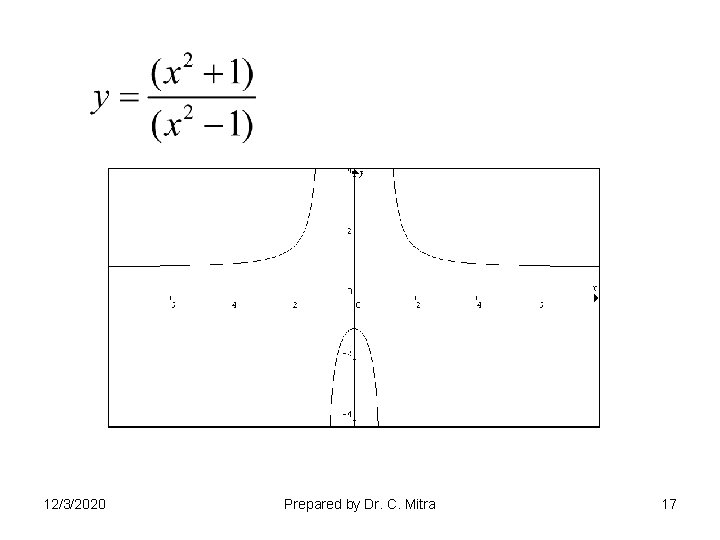
12/3/2020 Prepared by Dr. C. Mitra 17

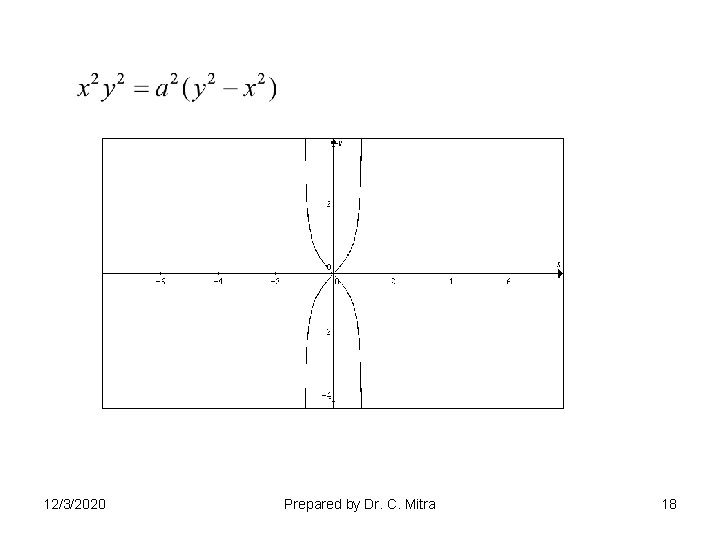
12/3/2020 Prepared by Dr. C. Mitra 18

12/3/2020 Prepared by Dr. C. Mitra 19

Symmetry: : • • • 12/3/2020 About the initial line: Replace by no change in the equation. About Pole: Replace r by -r no change in the equation. About the line perpendicular to the initial line (Y axis): Replace by and r by - r. OR replace by no change in the equation. Prepared by Dr. C. Mitra 20

Pole : : If for certain value of , r=0 the curve will pass through the pole. • Tangents at pole: Equate r=0 and solve for , lines =constant are tangents at the pole. • Prepare table of values of r and. 12/3/2020 Prepared by Dr. C. Mitra 21

• Angle between tangent and radius vector: : be angle between tangent and radius vector then , • tangent and radius vector coincides and • tangent and radius vector are perpendicular. 12/3/2020 Prepared by Dr. C. Mitra 22

Region of absence: • If for < < , r 2 <0, then no curve lie between = , = . • |sin | 1, |cos | 1. So for the curves r = acos n , r = asin n , r a. So, no curve lies outside the circle of radius r. • In most of the polar equations, only functions sin , cos occurs and so values of between 0 to 2 should be considered. The remaining values of , gives no new branch of the curve. 12/3/2020 Prepared by Dr. C. Mitra 23

Polar Curves Type I Sine curve can be obtained from corresponding cosine by rotating the plane through an angle /2 n. 12/3/2020 Prepared by Dr. C. Mitra 24

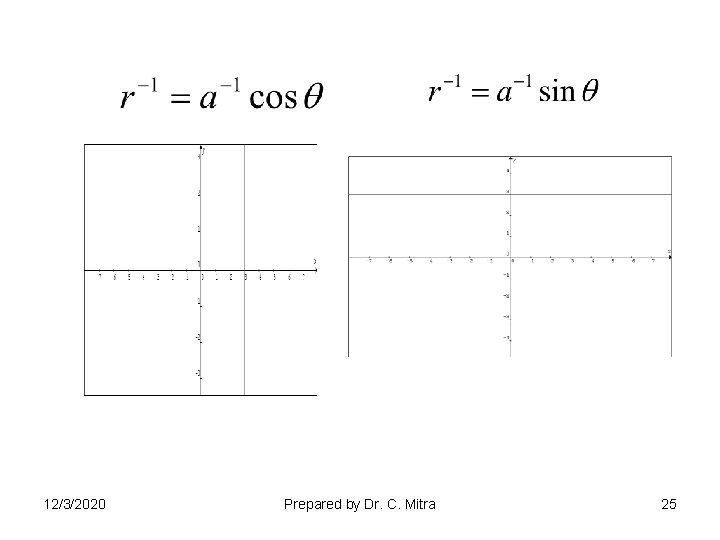
12/3/2020 Prepared by Dr. C. Mitra 25

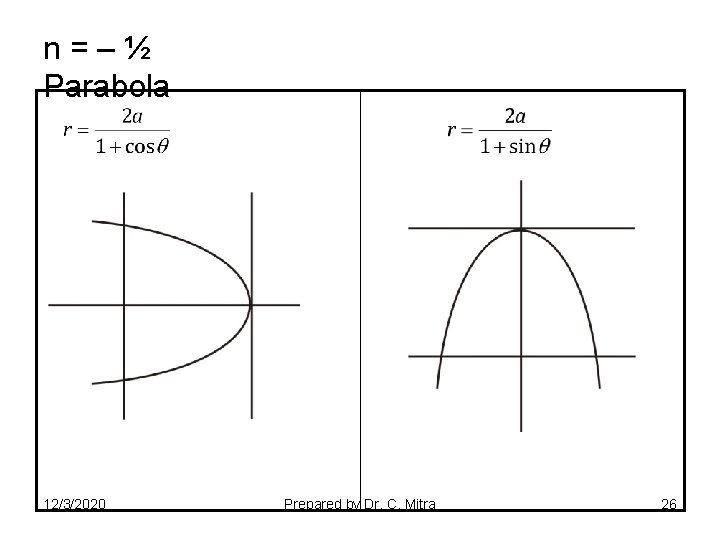
n=–½ Parabola 12/3/2020 Prepared by Dr. C. Mitra 26

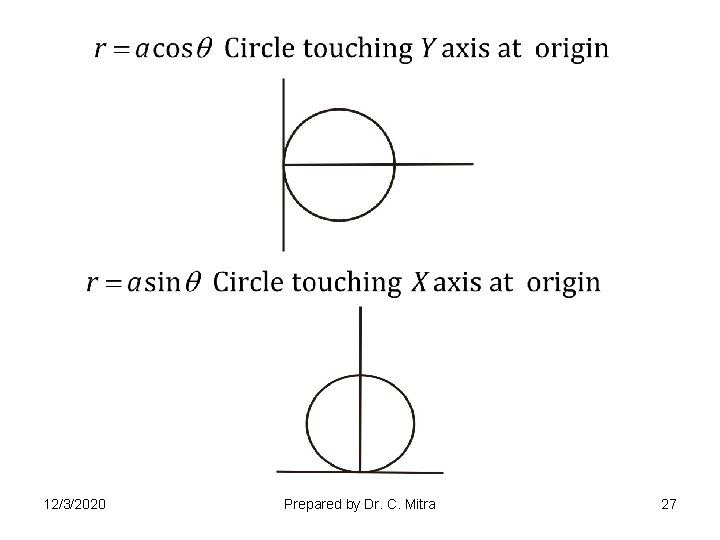
12/3/2020 Prepared by Dr. C. Mitra 27

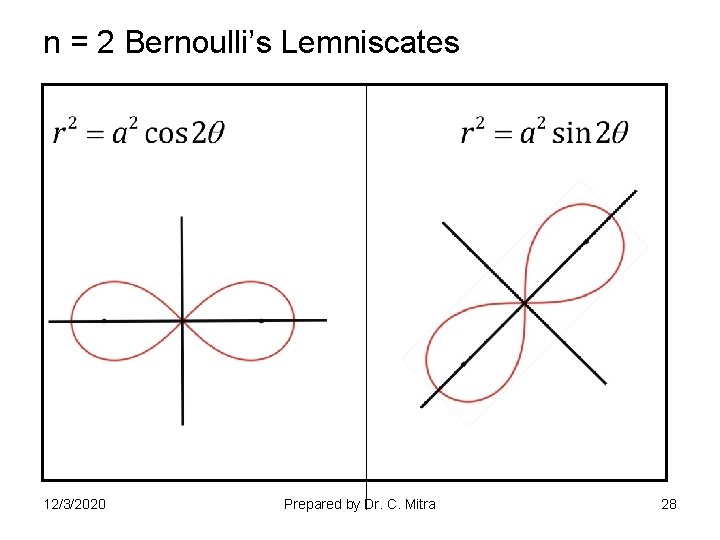
n = 2 Bernoulli’s Lemniscates 12/3/2020 Prepared by Dr. C. Mitra 28

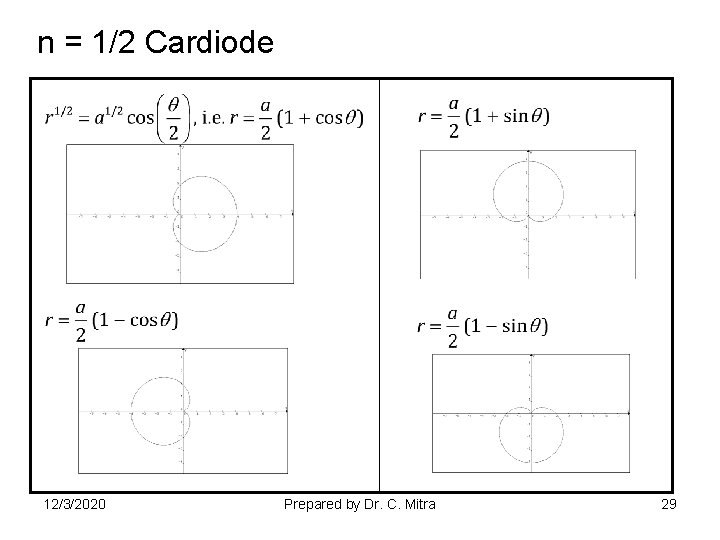
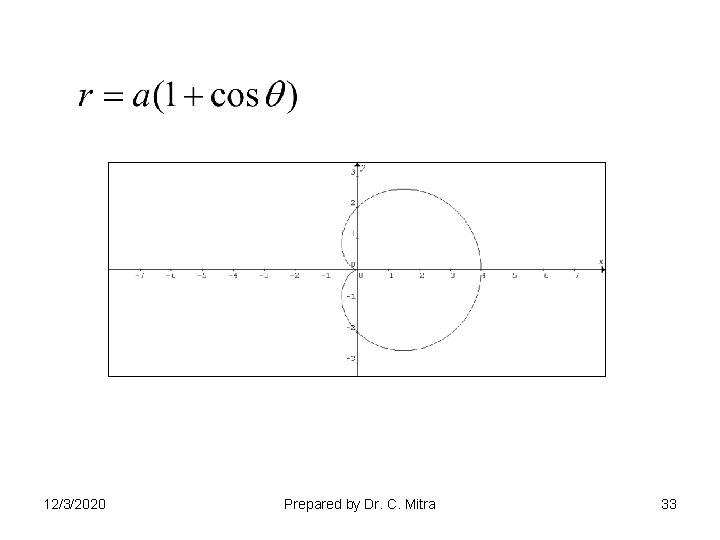
n = 1/2 Cardiode 12/3/2020 Prepared by Dr. C. Mitra 29

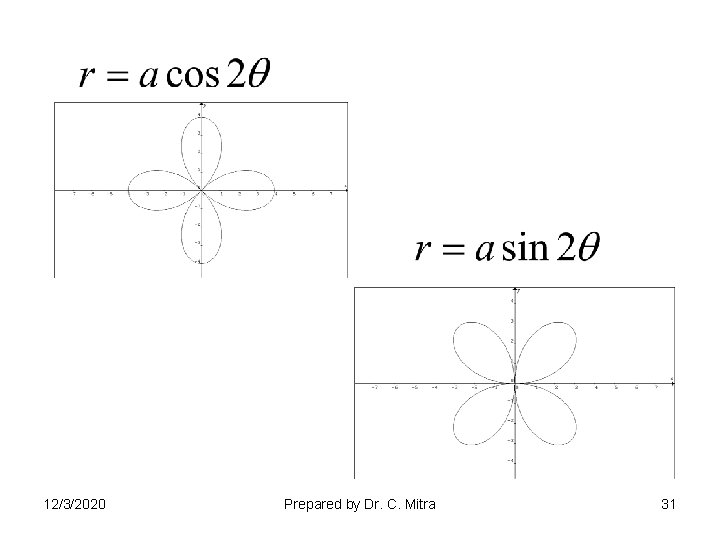
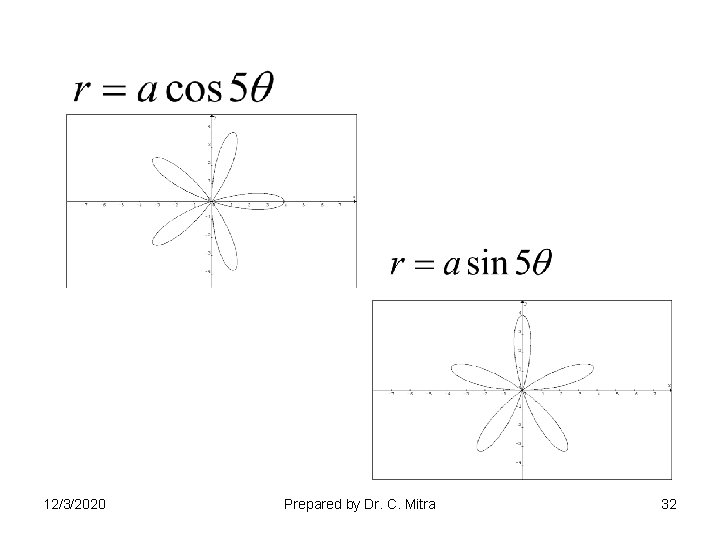
Type II Rose Curves Type III Type IV Spirals 12/3/2020 Prepared by Dr. C. Mitra 30

12/3/2020 Prepared by Dr. C. Mitra 31

12/3/2020 Prepared by Dr. C. Mitra 32

12/3/2020 Prepared by Dr. C. Mitra 33

12/3/2020 Prepared by Dr. C. Mitra 34

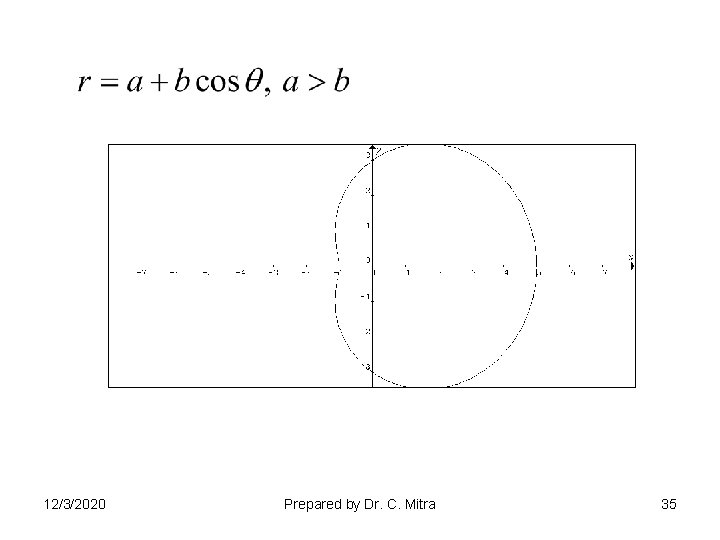
12/3/2020 Prepared by Dr. C. Mitra 35

12/3/2020 Prepared by Dr. C. Mitra 36

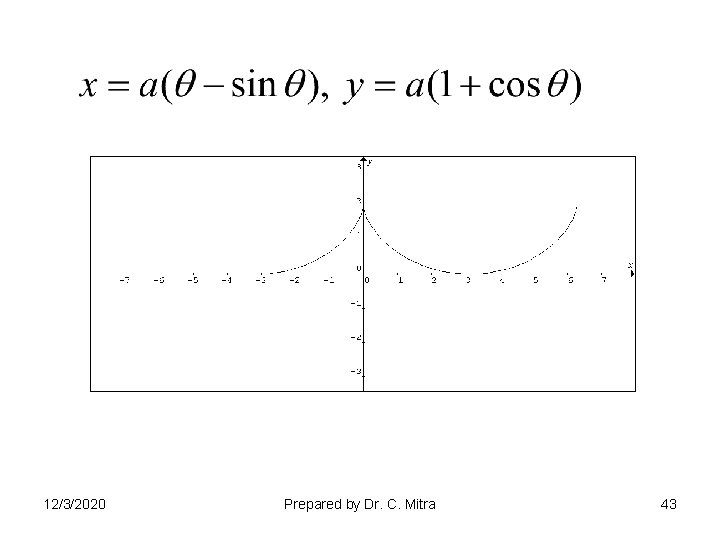
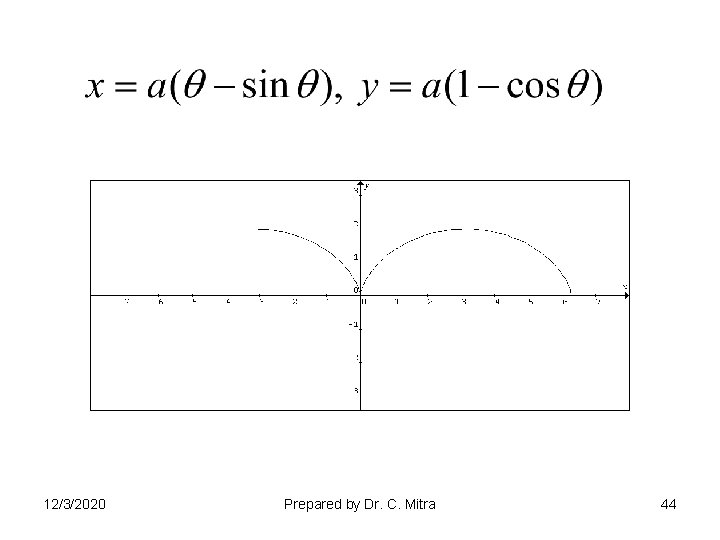
Symmetry : : • About X axis – Replace t by –t , x remain unchanged and y changes the sign then curve is symmetric about X- axis. • About Y axis - Replace t by –t , x changes the sign and y remain unchanged then curve is symmetric about Y- axis. • Note that : : For trigonometric equation replacing t by , y remains unchanged and x changes the sign curve will be symmetric about Y- axis. • About Origin - Replace t by –t both x and y changes the sign curve is symmetric about origin. 12/3/2020 Prepared by Dr. C. Mitra 37

• Points of Intersections : : – – • • 12/3/2020 If for some value of t, both x and y are zero curve passes through origin. Find X and Y intercepts. Find asymptotes if any. Find region of absence. Prepared by Dr. C. Mitra 38

• Tangents Find 12/3/2020 Prepared by Dr. C. Mitra 39

12/3/2020 Prepared by Dr. C. Mitra 40

12/3/2020 Prepared by Dr. C. Mitra 41

12/3/2020 Prepared by Dr. C. Mitra 42

12/3/2020 Prepared by Dr. C. Mitra 43

12/3/2020 Prepared by Dr. C. Mitra 44

WITCHES OF AGNESI The curve is obtained by drawing a line OB from the origin through the circle of radius a and center (0, a), then picking the point with the y coordinate of the intersection with the circle and the x coordinate of the intersection of the extension of line OB with the line y=2 a. 12/3/2020 Prepared by Dr. C. Mitra 45

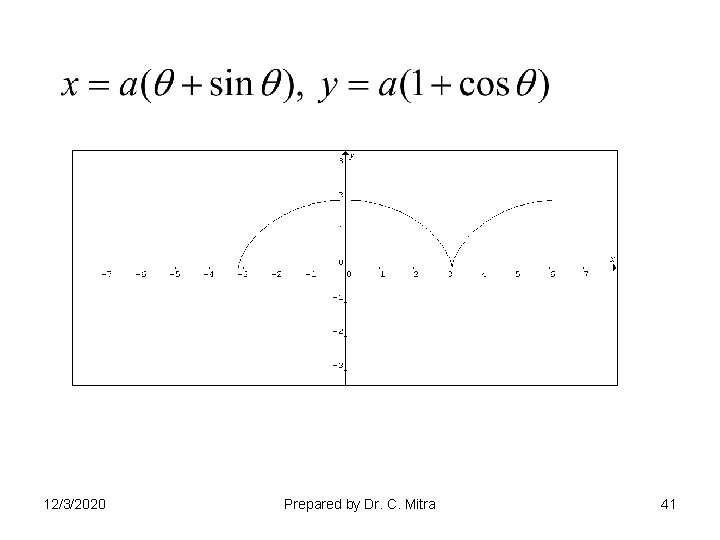
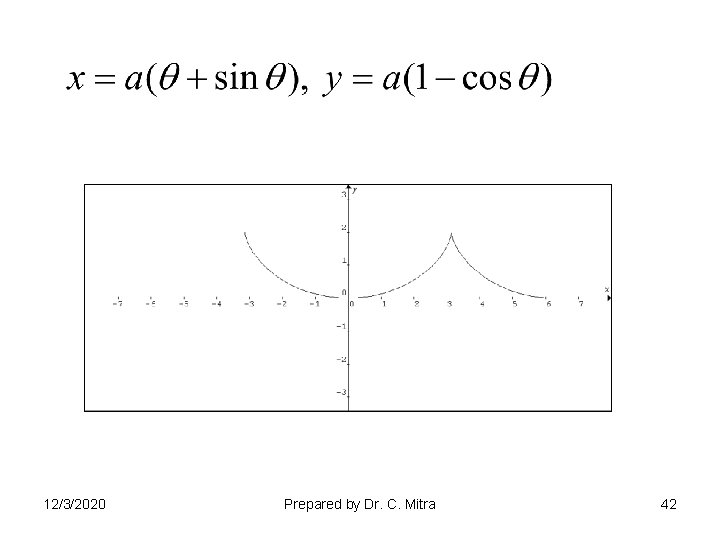
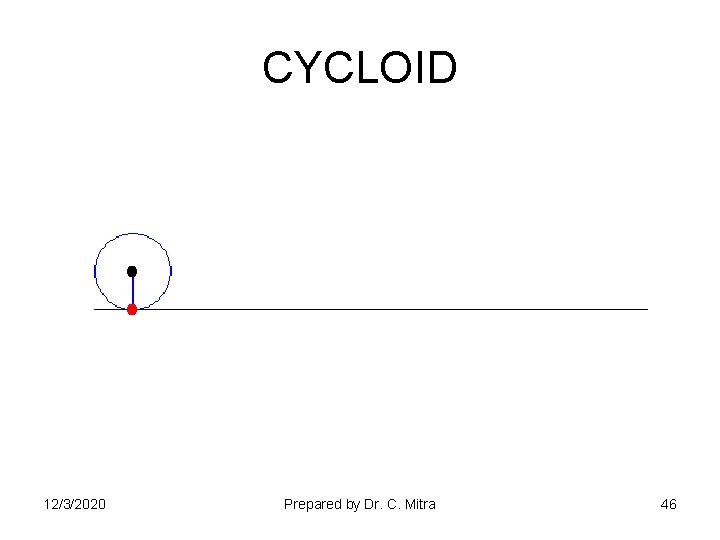
CYCLOID 12/3/2020 Prepared by Dr. C. Mitra 46

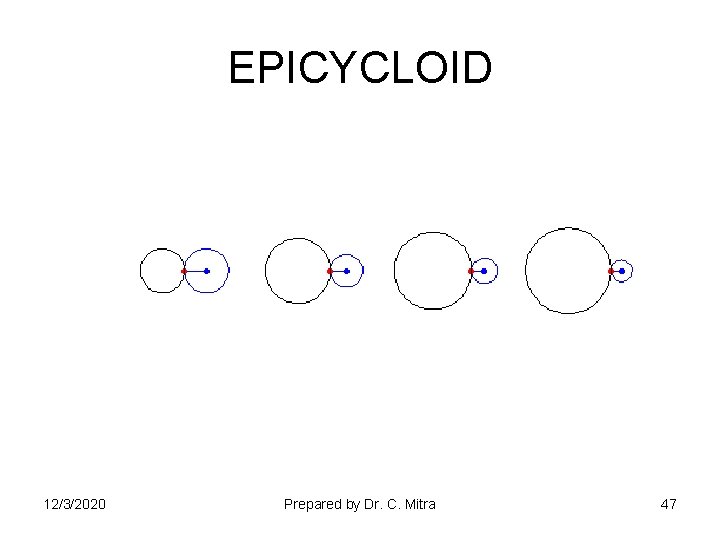
EPICYCLOID 12/3/2020 Prepared by Dr. C. Mitra 47

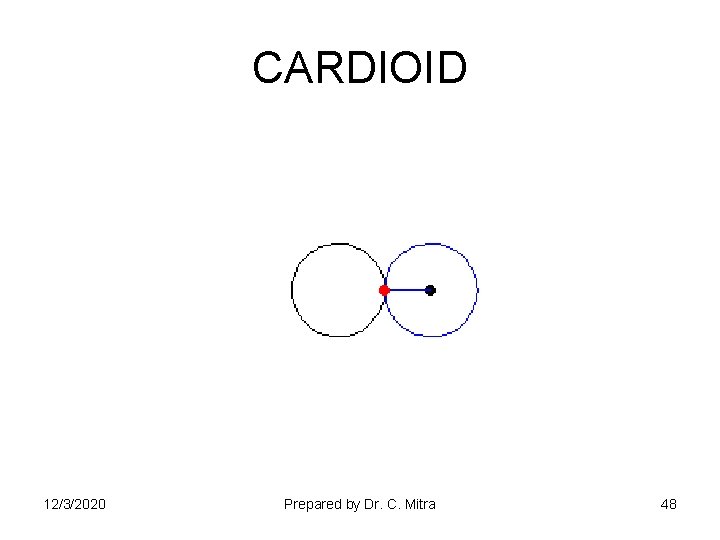
CARDIOID 12/3/2020 Prepared by Dr. C. Mitra 48

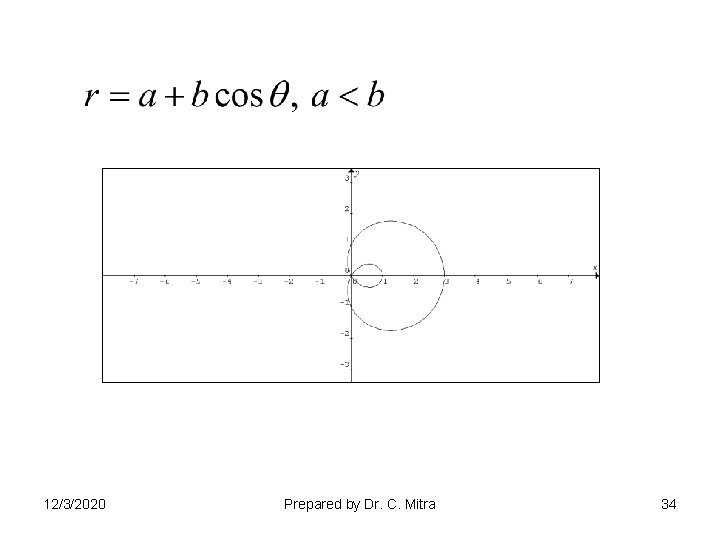
PASCAL’S LIMACON 12/3/2020 Prepared by Dr. C. Mitra 49

PASCAL’S LIMACON Let P be a point and C be a circle whose center is not P. Then the envelope of those circles whose center lies on C and that pass through P is a limaçon. 12/3/2020 Prepared by Dr. C. Mitra 50

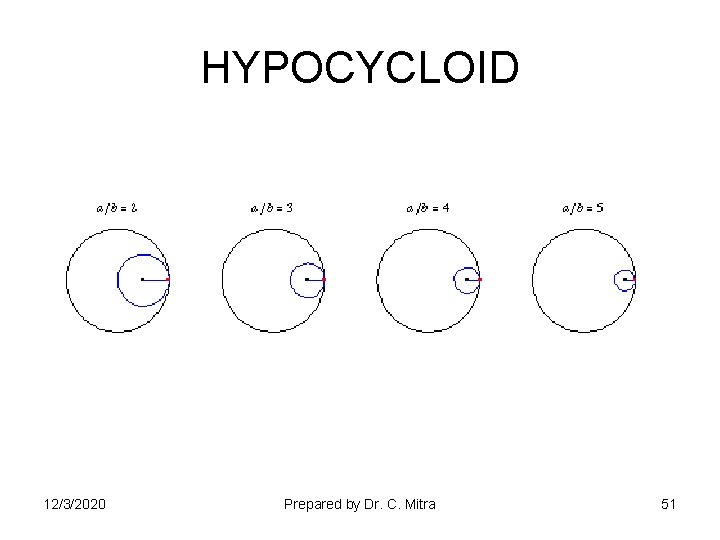
HYPOCYCLOID 12/3/2020 Prepared by Dr. C. Mitra 51

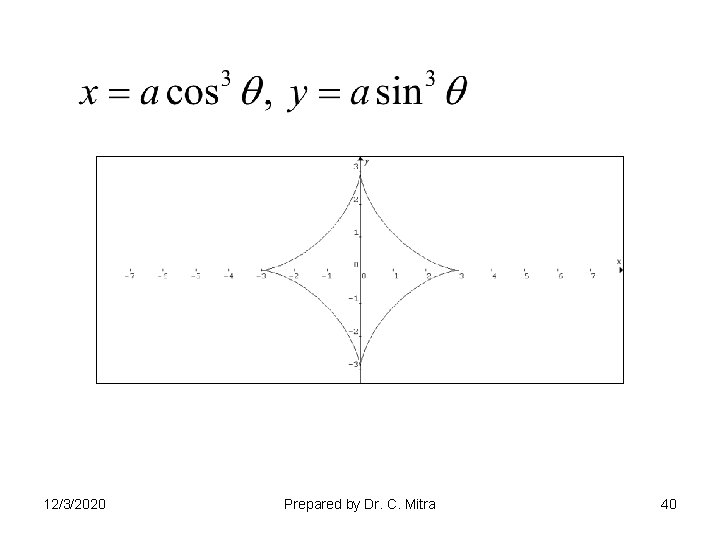
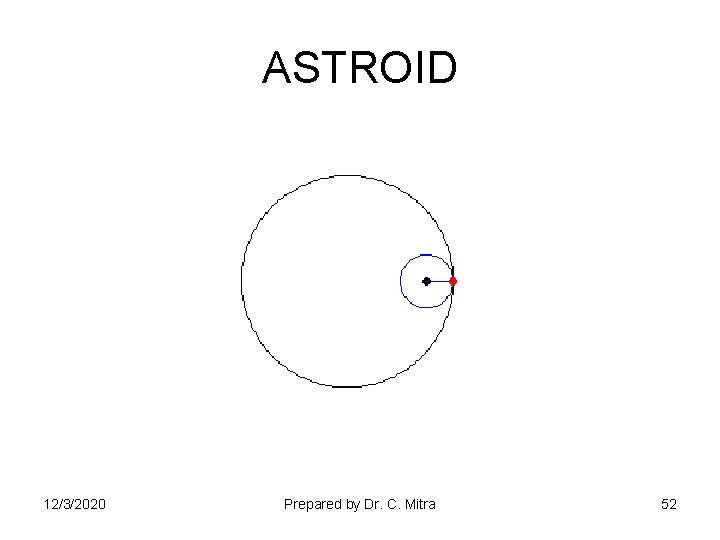
ASTROID 12/3/2020 Prepared by Dr. C. Mitra 52

12/3/2020 Prepared by Dr. C. Mitra 53

12/3/2020 Prepared by Dr. C. Mitra 54

12/3/2020 Prepared by Dr. C. Mitra 55