Warm up 1 Rewrite in slope intercept form

Warm up 1. Rewrite in slope intercept form: 3 x + 5 y = 15. 2. Rewrite in slope intercept form: x = 15 - 5 y 3. Factor: x 2 + 6 x + 9 4. Factor: x 2 - 10 x + 25 5. Expand (by FOIL): (x-7)2

Math is brought to you by the number … • April 15, 2013 • Day 62 of 90 • 90 -62 =

Graphing Quadratic Functions y = ax 2 + bx + c

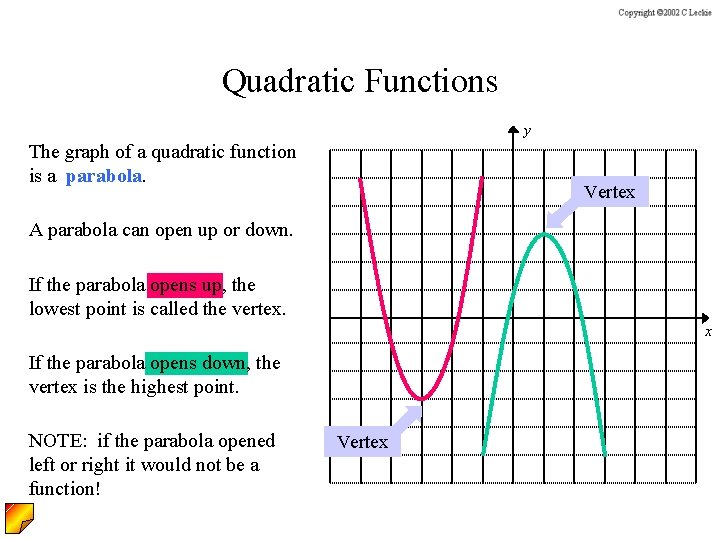
Quadratic Functions y The graph of a quadratic function is a parabola. Vertex A parabola can open up or down. If the parabola opens up, the lowest point is called the vertex. x If the parabola opens down, the vertex is the highest point. NOTE: if the parabola opened left or right it would not be a function! Vertex

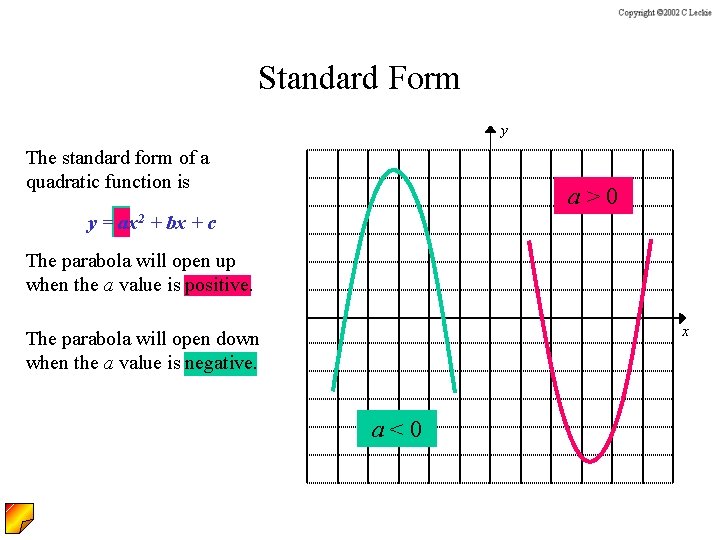
Standard Form y The standard form of a quadratic function is a>0 y = ax 2 + bx + c The parabola will open up when the a value is positive. x The parabola will open down when the a value is negative. a<0

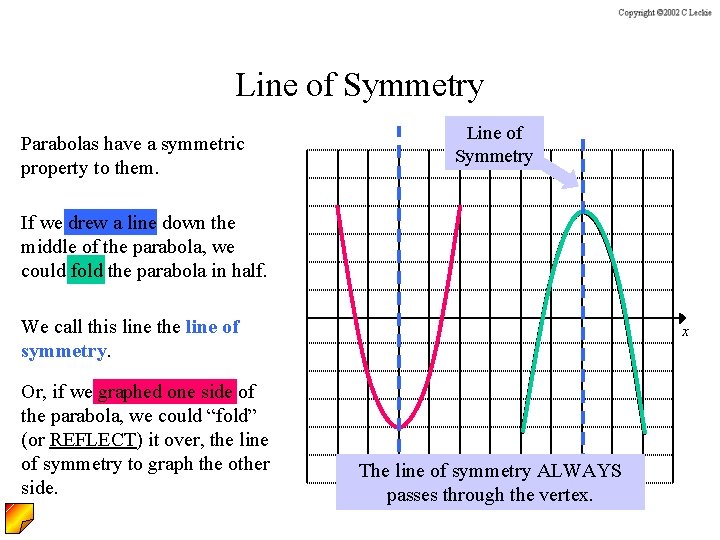
Line of Symmetry Parabolas have a symmetric property to them. Lineyof Symmetry If we drew a line down the middle of the parabola, we could fold the parabola in half. We call this line the line of symmetry. Or, if we graphed one side of the parabola, we could “fold” (or REFLECT) it over, the line of symmetry to graph the other side. x The line of symmetry ALWAYS passes through the vertex.

Finding the Line of Symmetry When a quadratic function is in standard form y = ax 2 + bx + c, The equation of the line of symmetry is For example… Find the line of symmetry of y = 3 x 2 – 18 x + 7 Using the formula… This is best read as … the opposite of b divided by the quantity of 2 times a. Thus, the line of symmetry is x = 3.

Finding the Vertex We know the line of symmetry always goes through the vertex. Thus, the line of symmetry gives us the x – coordinate of the vertex. To find the y – coordinate of the vertex, we need to plug the x – value into the original equation. y = – 2 x 2 + 8 x – 3 STEP 1: Find the line of symmetry STEP 2: Plug the x – value into the original equation to find the y value. y = – 2(2)2 + 8(2) – 3 y = – 2(4)+ 8(2) – 3 y = – 8+ 16 – 3 y=5 Therefore, the vertex is (2 , 5)

A Quadratic Function in Standard Form The standard form of a quadratic function is given by There are 3 steps to graphing a parabola in standard form. y = ax 2 + bx + c STEP 1: Find the line of symmetry STEP 2: Find the vertex STEP 3: Find two other points and reflect them across the line of symmetry. Then connect the five points with a smooth curve. MAKE A USE Plugthe in equation the. TABLE line of symmetry (x – value) to using x – values close to obtain the y – value of the line of symmetry. vertex.

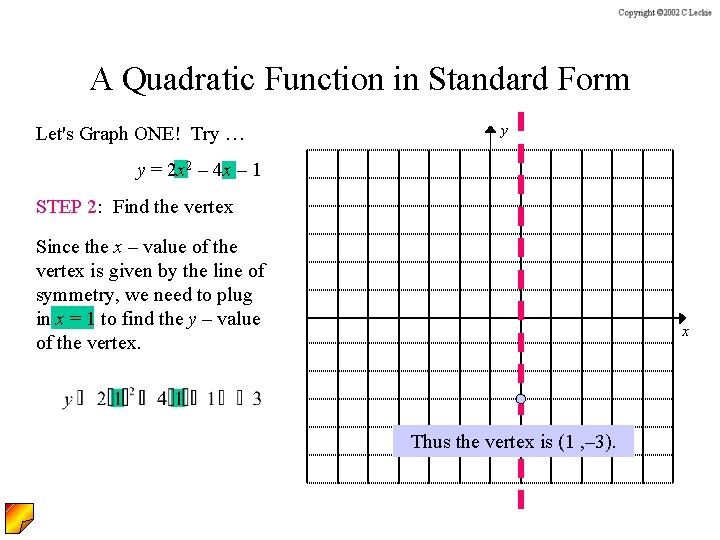
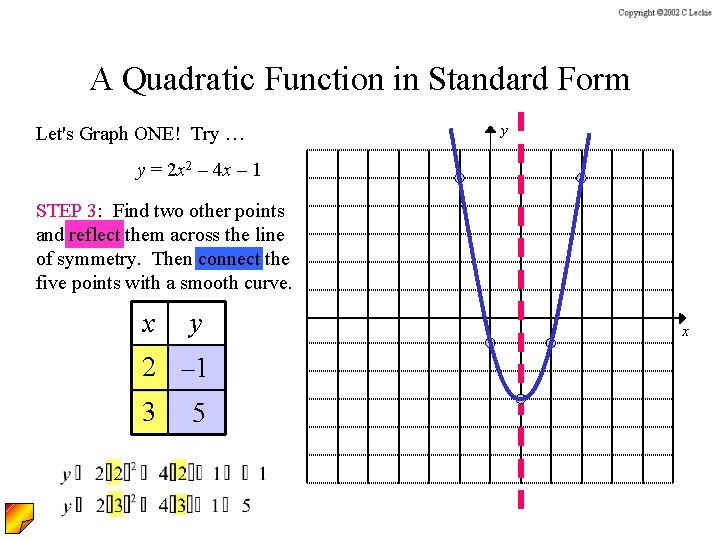
A Quadratic Function in Standard Form Let's Graph ONE! Try … y y = 2 x 2 – 4 x – 1 STEP 1: Find the line of symmetry x Thus the line of symmetry is x = 1

A Quadratic Function in Standard Form Let's Graph ONE! Try … y y = 2 x 2 – 4 x – 1 STEP 2: Find the vertex Since the x – value of the vertex is given by the line of symmetry, we need to plug in x = 1 to find the y – value of the vertex. x Thus the vertex is (1 , – 3).

A Quadratic Function in Standard Form Let's Graph ONE! Try … y y = 2 x 2 – 4 x – 1 STEP 3: Find two other points and reflect them across the line of symmetry. Then connect the five points with a smooth curve. x y 2 – 1 3 5 x

3. 2 Graphing Quadratic Functions in Vertex Form

Vertex Form Equation y=a(x-h)2+k • If a is positive, parabola opens up If a is negative, parabola opens down. • The vertex is the point (h, k). • The axis of symmetry is the vertical line x=h.

Vertex Form v Each function we just looked at can be written in the form (x – h)2 + k, where (h , k) is the vertex of the parabola, and x = h is its axis of symmetry. v(x – h)2 + k – vertex form Equation Vertex Axis of Symmetry y = x 2 or y = (x – 0)2 + 0 (0 , 0) x=0 y = x 2 + 2 or y = (x – 0)2 + 2 (0 , 2) x=0 y = (x – 3)2 or y = (x – 3)2 + 0 (3 , 0) x=3

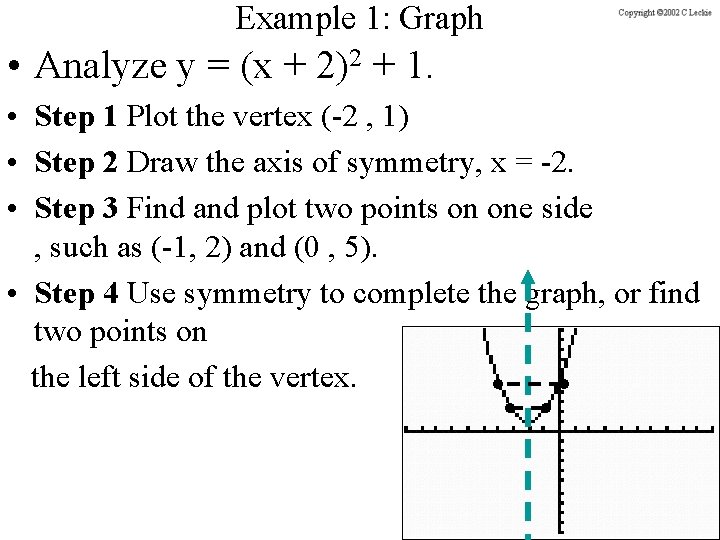
Example 1: Graph • Analyze y = (x + 2)2 + 1. • Step 1 Plot the vertex (-2 , 1) • Step 2 Draw the axis of symmetry, x = -2. • Step 3 Find and plot two points on one side , such as (-1, 2) and (0 , 5). • Step 4 Use symmetry to complete the graph, or find two points on the left side of the vertex.

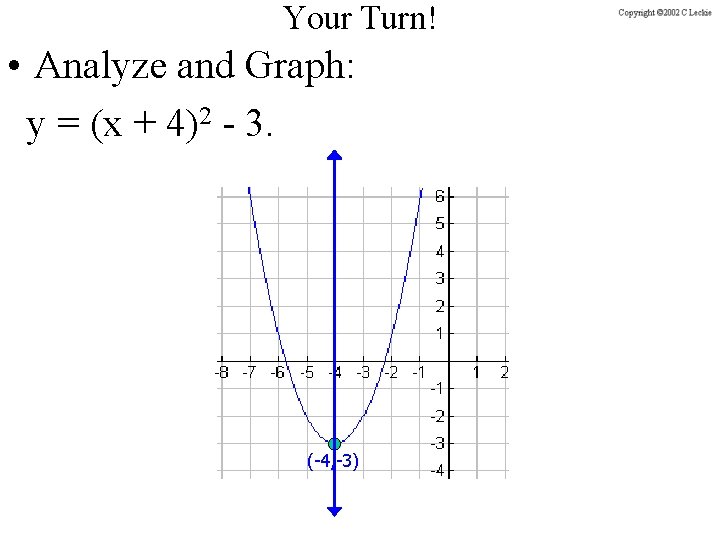
Your Turn! • Analyze and Graph: y = (x + 4)2 - 3. (-4, -3)

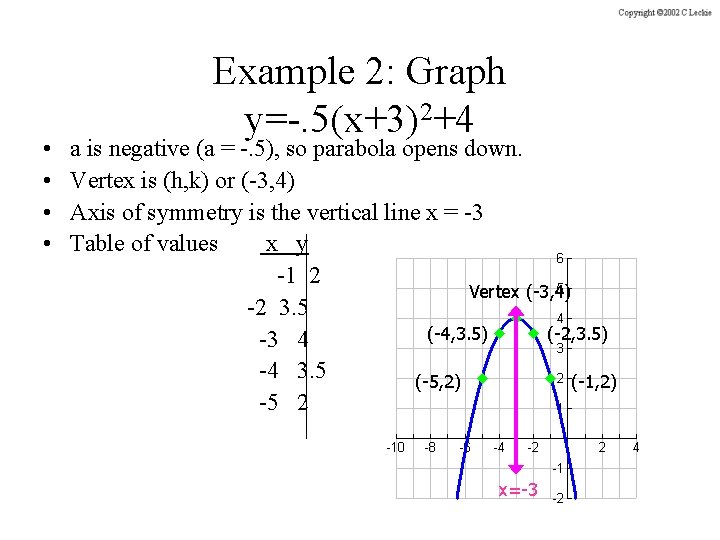
• • Example 2: Graph y=-. 5(x+3)2+4 a is negative (a = -. 5), so parabola opens down. Vertex is (h, k) or (-3, 4) Axis of symmetry is the vertical line x = -3 Table of values x y -1 2 Vertex (-3, 4) -2 3. 5 (-4, 3. 5) (-2, 3. 5) -3 4 -4 3. 5 (-5, 2) (-1, 2) -5 2 x=-3

Now you try one! y=2(x-1)2+3 • Open up or down? • Vertex? • Axis of symmetry? • Table of values with 5 points?

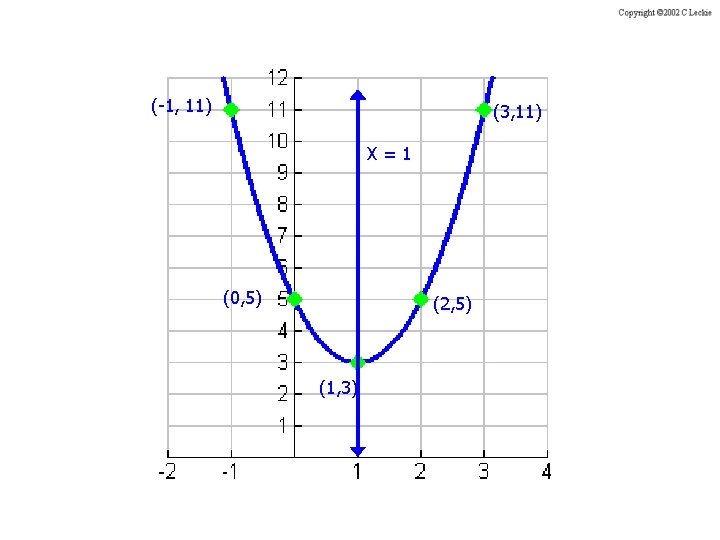
(-1, 11) (3, 11) X=1 (0, 5) (2, 5) (1, 3)

Write an equation for the parabola whose vertex is at (1, 2) and passes through (3, 4). The vertex of the parabola is at (1, 2) so and Since (3, 4) is a point on the graph of the parabola , and Substitute these values into the vertex form of the equation and solve for a. Vertex form Substitute 1 for h, 2 for k, 3 for x, and 4 for y. Simplify.

Subtract 2 from each side. Divide each side by 4. Answer: The equation of the parabola in vertex form is

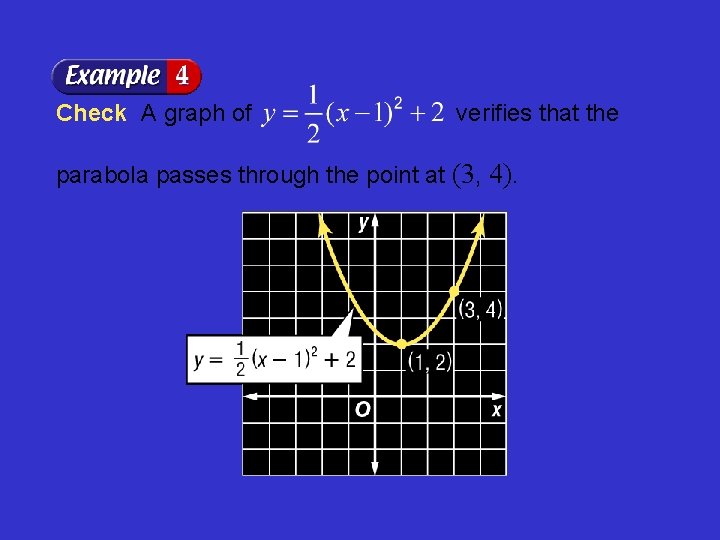
Check A graph of verifies that the parabola passes through the point at (3, 4).

Write an equation for the parabola whose vertex is at (2, 3) and passes through (– 2, 1). Vertex form 1 = a(-2 – 2)2 + 3 Substitute 2 for h, 3 for k, -2 for x, and 1 for y. 1 = 16 a + 3 -2 = 16 a -1/8 = a Answer: