Chapter 4 Interpolation and Approximation 4 1 Lagrange

Chapter 4 Interpolation and Approximation

4. 1 Lagrange Interpolation n The basic interpolation problem can be posed in one of two ways:

Example 4. 1 e-1/2

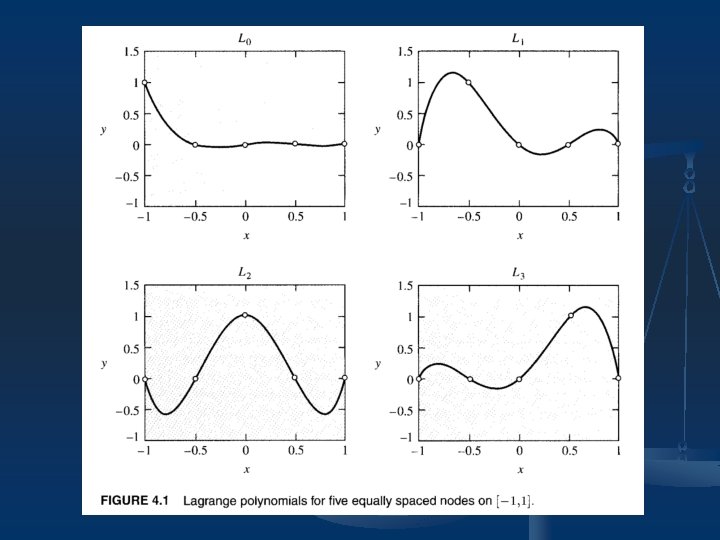
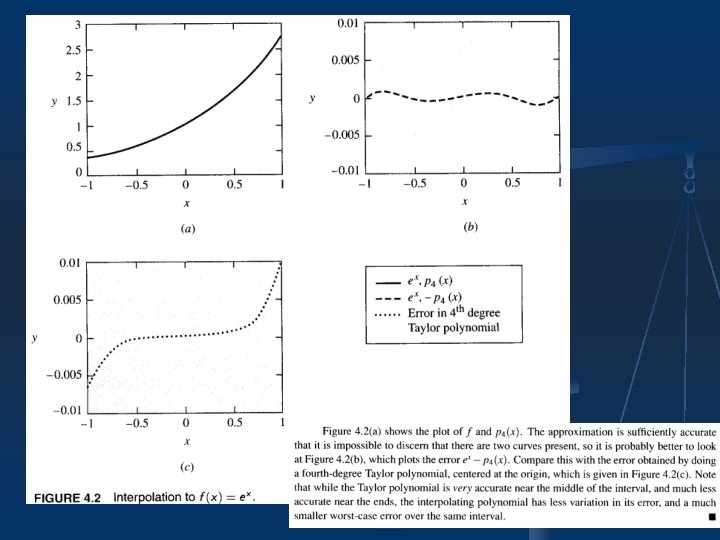
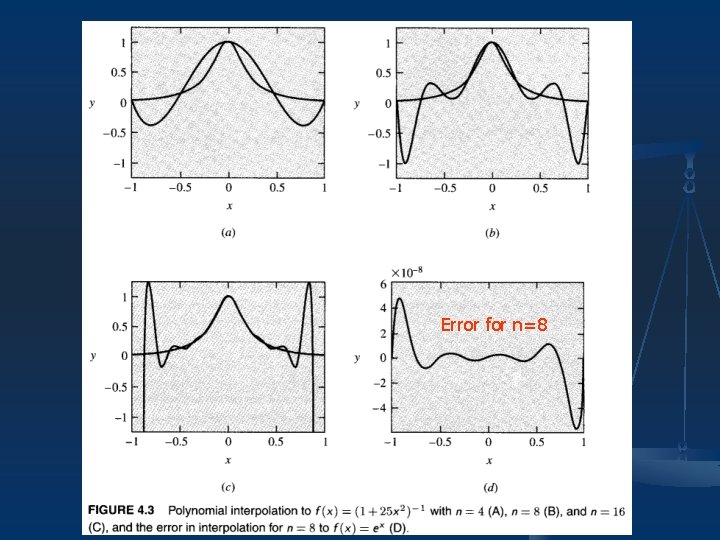
Discussion n The construction presented in this section is called Lagrange interpolation. How good is interpolation at approximating a function? (Sections 4. 3, 4. 11) Consider another example: n If we use a fourth-degree interpolating polynomial to approximate this function, the results are as shown in Figure 4. 3 (a).

Error for n=8

Discussion n n There are circumstances in which polynomial interpolation as approximation will work very well, and other circumstances in which it will not. The Lagrange form of the interpolating polynomial is not well suited for actual computations, and there is an alternative construction that is far superior to it.

4. 2 Newton Interpolation and Divided Differences n The disadvantage of the Lagrange form n n If we decide to add a point to the set of nodes, we have to completely recompute all of the functions. Here we introduce an alternative form of the polynomial: the Newton form. n It can allow us to easily write in terms of

=0

Example 4. 2

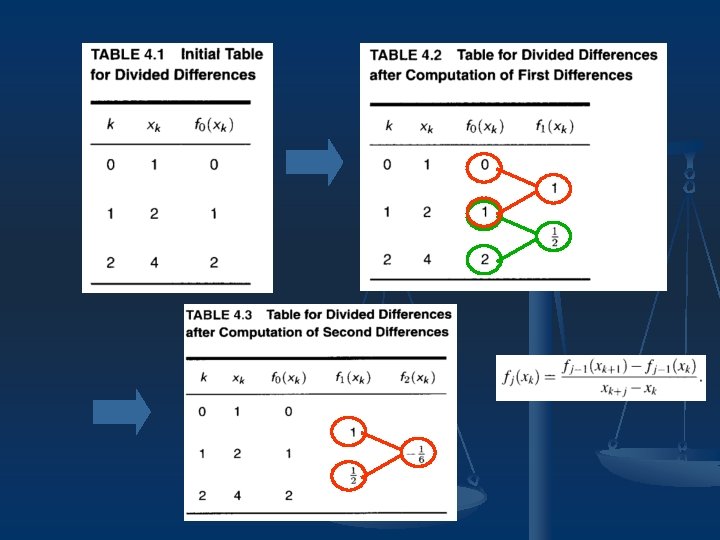
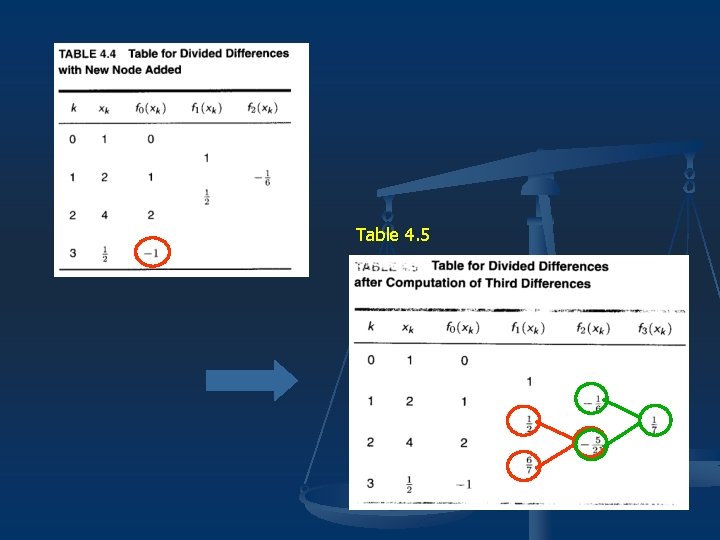
Discussion n n The coefficients are called divided differences. We can use divided-difference table to find them.

Example 4. 3

Example 4. 3 (Con. )

Table 4. 5

4. 3 Interpolation Error

Norms n The infinity norm of pointwise norm: n The 2 -norm:

The interpolation error of linear interpolation

Example 4. 5

Example 4. 5 (Con. )

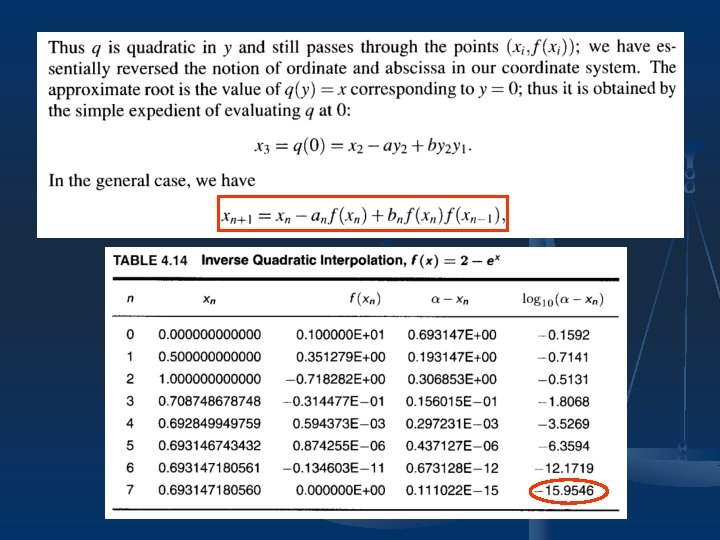
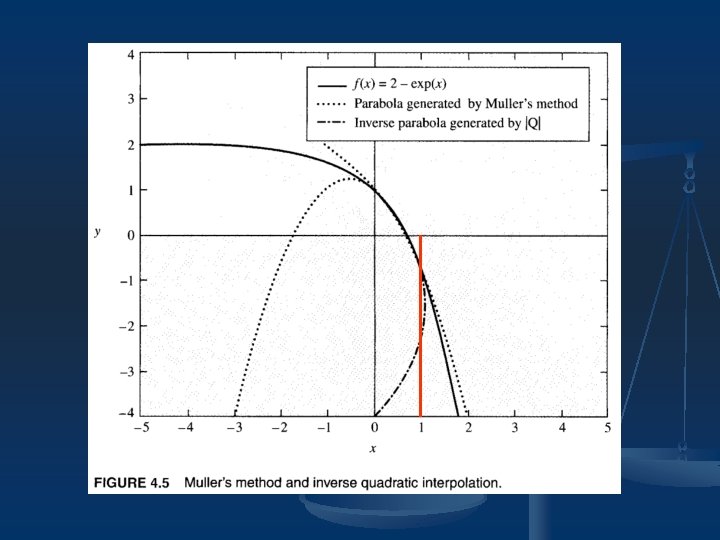
4. 4 Application: Muller’s Method and Inverse Quadratic Interpolation n We can use the idea of interpolation to develop more sophisticated root-finding methods. For example: Muller’s Method Given three points we find the quadratic polynomial such that 0, 1, 2; and then define as the root of that is closest to.

compare

An Alternative to Muller’s Method n Inverse quadratic interpolation:

Discussion n n One great utility of Muller’s method is that it is able to find complex roots of real-valued functions, because of the square root in the computation. Inverse quadratic interpolation is used as part of Brent. Dekker root-finding algorithm, which is a commonly implemented automatic root-finding program.

4. 5 Application: More Approximations to the Derivative depends on x

4. 5 Application: More Approximations to the Derivative n The interpolating polynomial in Lagrange form is n The error is given as in (4. 20), thus n We get

We can use above equations to get:

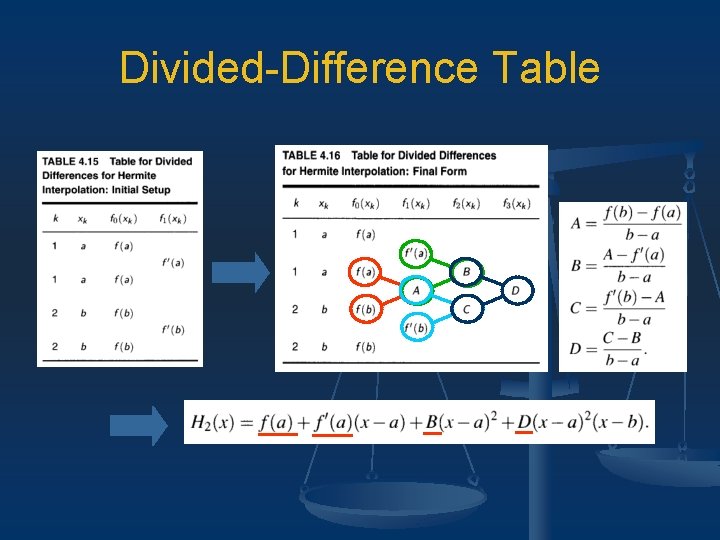
4. 6 Hermite Interpolation n Hermite interpolation problem: n Can we do this? Yes.

Divided-Difference Table

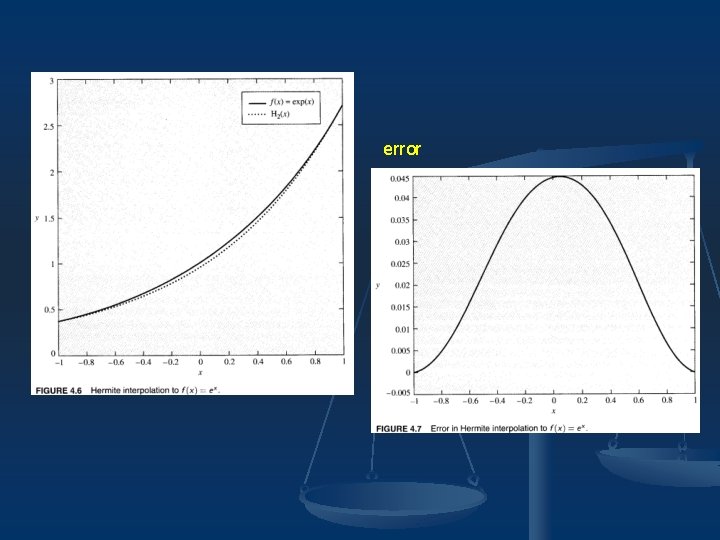
An example

error

Hermite Interpolation Error Theorem

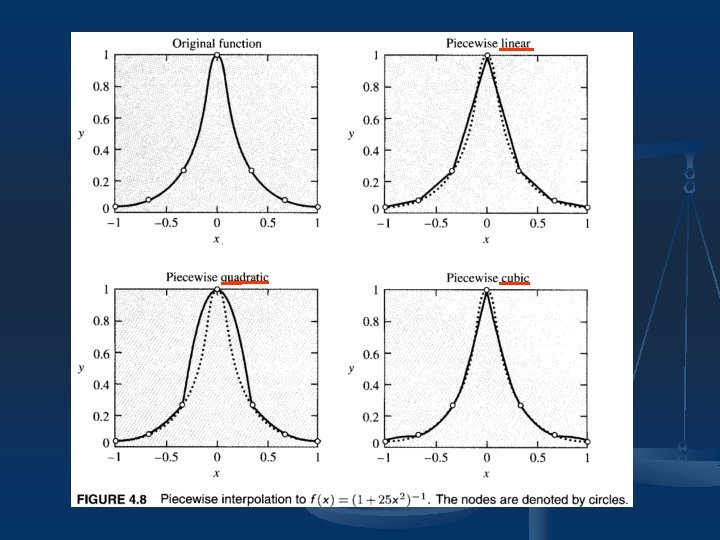
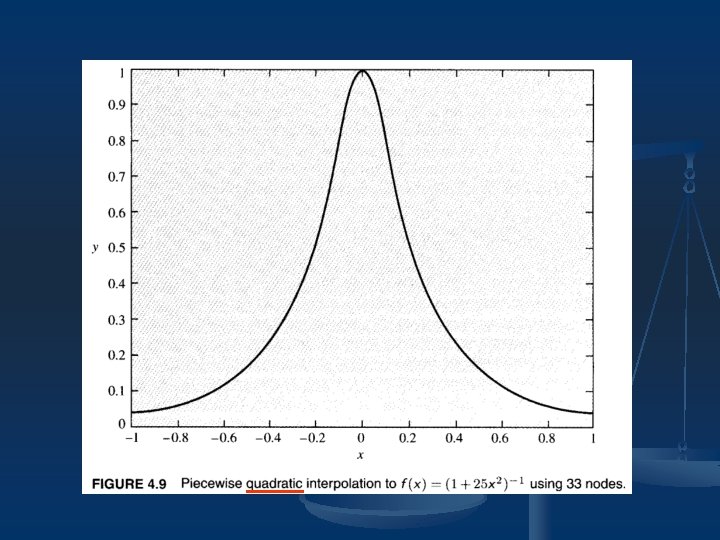
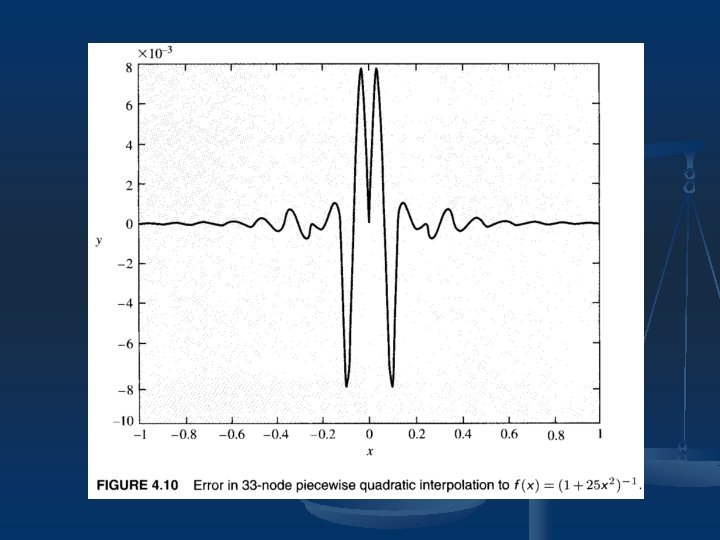
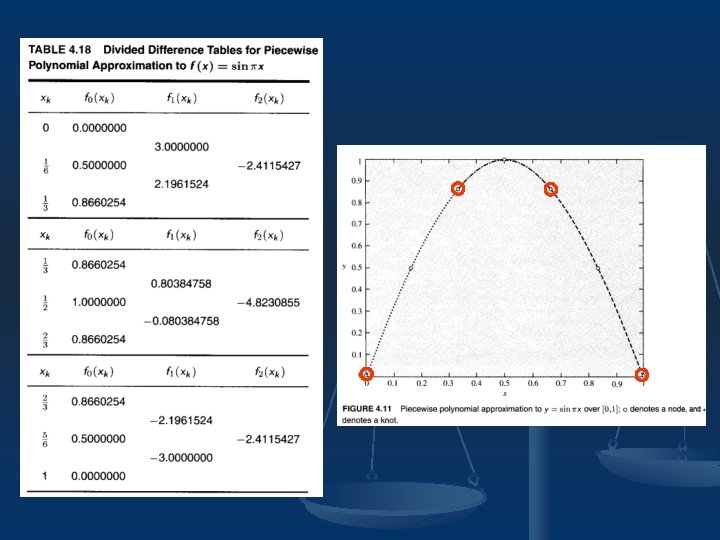
4. 7 Piecewise Polynomial Interpolation n n If we keep the order of the polynomial fixed and use different polynomials over different intervals, with the length of the intervals getting smaller and smaller, then interpolation can be a very accurate and powerful approximation tool. For example:

Example 4. 6