Chapter 3 Interpolation and Polynomial Approximation Hermite Interpolation

Chapter 3 Interpolation and Polynomial Approximation -- Hermite Interpolation 3. 3 Hermite Interpolation Find the osculating polynomial P(x) such that P(xi) = f (xi), P’ (xi) = f ’ (xi), …, P(m_i) (xi) = f (m_i) (xi) for all i = 0, 1, …, n. Note: Given N conditions (and hence N equations), a polynomial of degree N 1 can be determined. The osculating polynomial that agrees with f and all its derivatives of order m 0 at one point x 0 is just the Taylor polynomial with remainder The case when mi = 1 for each i = 0, 1, …, n gives the Hermite polynomials. 1/12

Chapter 3 Interpolation and Polynomial Approximation -- Hermite Interpolation Example: Suppose x 0 x 1 x 2. Given f(x 0), f(x 1), f(x 2) and f ’(x 1), find the polynomial P(x) such that P(xi) = f (xi)，i = 0, 1, 2, and P’(x 1) = f ’(x 1). Analyze the errors. 3. Solution: First of all, the degree of P(x) must be … Similar to Lagrange polynomials, we may assume the form of Hermite polynomial as 2 P 3 ( x ) = f ( x i ) hi ( x ) + f ’� ( x 1 ) h 1 ( x ) Similar to i = 0 Lagrange error analysis where hi(xj) = ij , hi’(x 1) = 0, h 1 (xi) = 0, h 1’(x 1) = 1 h 0(x) Has roots x 1, x 2, and h 0’(x 1) = 0 x 1 is a multiple root. h 0 ( x ) = C 0 ( x x 1 )2 ( x x 2 ) h 0(x 0) = 1 C 0 h 2(x) Similar to h 0(x). = + h 1(x) Has roots x 0, x 2 h 1 ( x ) ( Ax B )( x x 0 )( x x 2 ) A and B can be solved with h 1(x 1) = 1 and h 1’(x 1) = 0. Has roots x , x h 0 1 2 1( x ) = C 1 ( x x 0 )( x x 1 )( x x 2 ) h 1(x) ) = 1 C 1 can be solved. h’(x 1 1 2/12

Chapter 3 Interpolation and Polynomial Approximation -- Hermite Interpolation In general, given x 0 , …, xn; y 0 , …, yn and y 0’ , …, yn’. The Hermite polynomial H 2 n+1(x) satisfies H 2 n+1(xi) = yi and H’ 2 n+1(xi) = yi’ for all i. Solution: Let H 2 n+1( x ) = n i =0 yi hi ( x ) + n i =0 yi’ h i ( x ) )= where hi(xj) = ij, hi’(xj) = 0, hi (xj) = 0, h’(x ij i j hi(x) x 0 , …, xi , …, xn are all roots with multiplicity 2 hi ( x ) = ( Ai x + Bi )Ln, 2 i ( x ) Ai and Bi can be solved by hi(xi) = 1 and hi’(xi) = 0 Such a Hermite interpolating polynomial is unique hi (x) All the roots x 0 , …, xn have multiplicity 2 except xi hi( x) = Ci ( x xi ) Ln, i 2(x) hi(x) = ( x xi ) Ln, i 2(x) h’(x i i) = 1 Ci = 1 If 3/12 , then

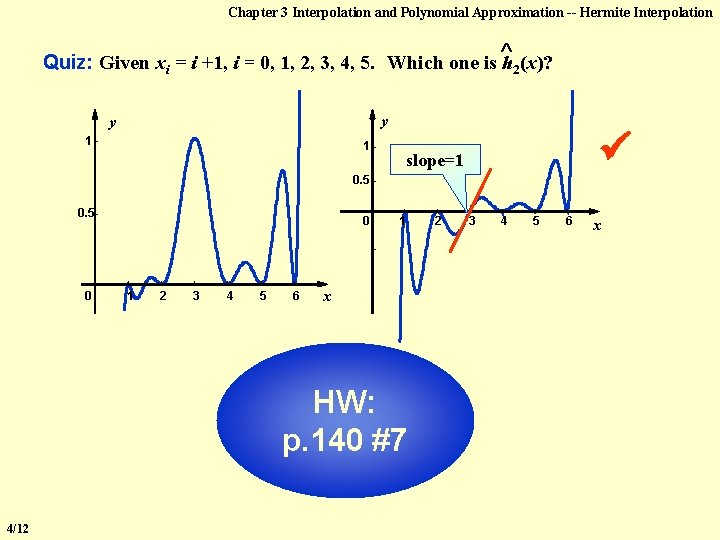
Chapter 3 Interpolation and Polynomial Approximation -- Hermite Interpolation Quiz: Given xi = i +1, i = 0, 1, 2, 3, 4, 5. Which one is h 2(x)? y y 1 - 1 - slope=1 0. 5 - 0 1 2 3 4 5 6 x HW: p. 140 #7 4/12 2 3 4 5 6 x

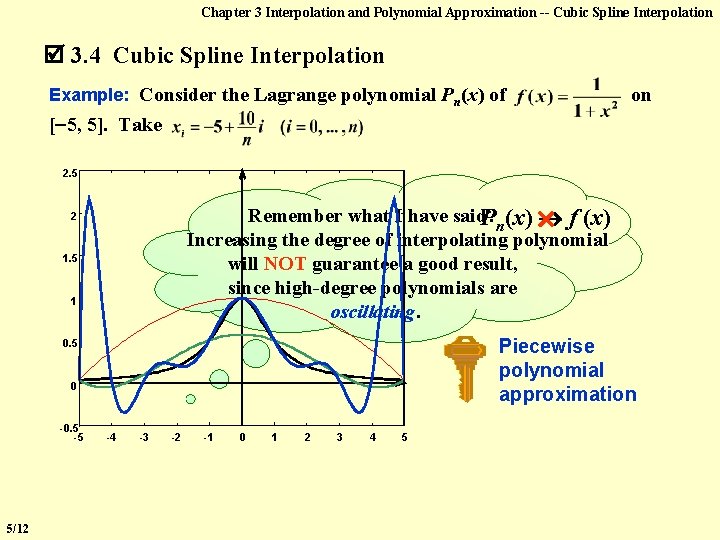
Chapter 3 Interpolation and Polynomial Approximation -- Cubic Spline Interpolation 3. 4 Cubic Spline Interpolation Example: Consider the Lagrange polynomial Pn(x) of on [ 5, 5]. Take 2. 5 Remember what I have said? Pn(x) f (x) Increasing the degree of interpolating polynomial will NOT guarantee a good result, since high-degree polynomials are oscillating. 2 1. 5 1 Piecewise polynomial approximation 0. 5 0 -0. 5 -5 5/12 -4 -3 -2 -1 0 1 2 3 4 5

Chapter 3 Interpolation and Polynomial Approximation -- Cubic Spline Interpolation Piecewise linear interpolation Approximate f (x) by linear polynomials on each subinterval Let . Then uniform as No longer smooth. How can we make a smooth Hermite piecewise polynomials interpolation without asking Given too much from f ? Construct the Hermite polynomial degree 3 with y and y’ on the Headacheof… two endpoints of . It is not easy to obtain the derivatives. 6/12 :

Chapter 3 Interpolation and Polynomial Approximation -- Cubic Spline Interpolation Cubic Spline Definition: Given a function f defined on [a, b] and a set of nodes a = x 0 < x 1 < … < xn = b, a cubic spline interpolant S for f is a function that satisfies the following conditions: a. S(x) is a cubic polynomial, denoted Si(x), on the subinterval [ xi , xi+1] for each i = 0, 1, …, n – 1; b. S(xi) = f (xi) for each i = 0, 1, …, n; c. Si+1(xi+1) = Si(xi+1) for each i = 0, 1, …, n – 2; d. S’i+1(xi+1) = S’i(xi+1) for each i = 0, 1, …, n – 2; e. S”i+1(xi+1) = S”i(xi+1) for each i = 0, 1, …, n – 2; f(x) H(x) S(x) 7/12

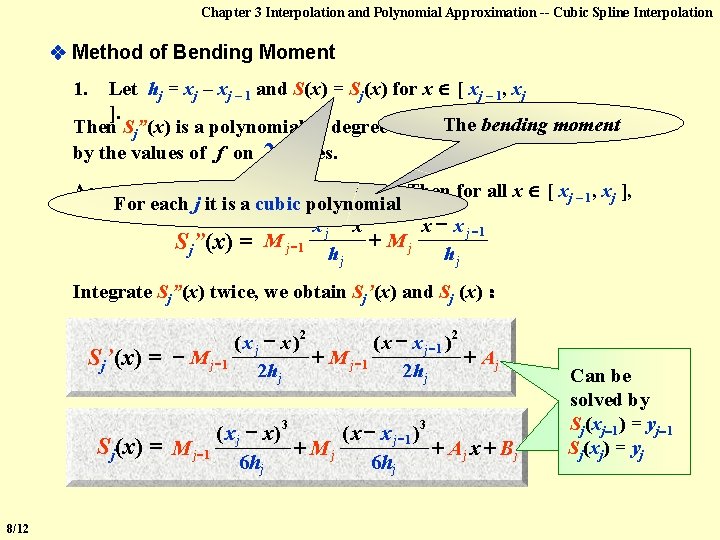
Chapter 3 Interpolation and Polynomial Approximation -- Cubic Spline Interpolation Method of Bending Moment Let hj = xj – 1 and S(x) = Sj(x) for x [ xj – 1, xj ]. The bending moment Then Sj”(x) is a polynomial of degree 1 , which can be determined by the values of f on 2 nodes. 1. Assume Sj”(xj 1) = Mj 1， Sj”(xj) = Mj. Then for all x [ xj – 1, xj ], For each j it is a cubic polynomial xj x x x j 1 Sj”(x) = M j 1 h + M j h j j Integrate Sj”(x) twice, we obtain Sj’(x) and Sj (x) ： Sj’(x) = ( x j x )2 ( x x j 1 ) 2 M j 1 + Aj 2 h j ( x j x) ( x x j 1 ) + Mj + Aj x + B j Sj(x) = M j 1 6 hj 3 8/12 3 Can be solved by Sj(xj 1) = yj 1 Sj(xj) = yj

Chapter 3 Interpolation and Polynomial Approximation -- Cubic Spline Interpolation yj 1 Mj 1 = Aj hj hj 6 M j 1 2 x j x M j 2 x x j 1 + ( yj Aj x + Bj = ( y j 1 hj ) h) 6 hj 6 j hj Now solve for Mj ： Since S’ is continuous at xj ( xj x)2 ( x xj 1 )2 Mj 1 + Mj + f [ xj 1 , xj ] hj [xj 1, xj ]: Sj’(x) = Mj 1 2 hj 6 2 2 ( x j+1 x) ( x xj ) Mj+1 Mj + Mj+1 + f [ xj , xj+1 ] hj+1 [xj , xj+1]: Sj+1’(x) = Mj 2 hj+1 6 From Sj’(xj) = Sj+1’(xj), we can combine the coefficients for Mj 1, Mj, and Mj+1. 6 h j +1 = g ( f [ x j , x j +1 ] - f [ x j -1 , x j ]) Define j = , j = 1 - j , and j hj +1 h j +1 j M j -1 + 2 M j + j M j + 1 = g j for 1 j n 1 That is, we have n+1 unknowns but only n 1 equations. Extra 2 boundary conditions are needed. 9/12

Chapter 3 Interpolation and Polynomial Approximation -- Cubic Spline Interpolation S’(a) = y 0’， S’(b) = yn’ /* Clamped boundary */ 2 M M 0 ( x 1 x) ( x a)2 + M 1 + f [ x 0 , x 1 ] 1 [ a , x 1 ]: S 1’(x) = M 0 h 1 2 h 1 6 2 M 0 + M 1 = 6 ( f [ x 0 , x 1 ] y 0 ’ ) = g 0 Similar for Sn’(x) on [ h 1 xn 1, b ] M n 1 + 2 M n = 6 ( yn’ f [ x n 1 , x n ]) = g n hn S”(a) = y 0” = M 0， S”(b) = yn” = Mn The case when M 0 = Mn = 0 is called a free boundary, and when that occurs, the spline is called a Natural Spline. Periodic boundary: If f is a periodic function, that is, yn = y 0 and S’(a+) = S’(b ) M 0 = Mn 10/12

Chapter 3 Interpolation and Polynomial Approximation -- Cubic Spline Interpolation Note: Cubic Spline can be uniquely determined by its boundary conditions as long as the coefficient matrix is strictly diagonally dominant. If f C[ a, b ] and . Then as max hi 0. That is, the accuracy of approximation can be improved by adding more nodes without increasing the degree of the splines. HW: p. 153 -154 #9, 17 Sketch of the Algorithm: Cubic Spline ② Solve for M ; Compute j , gj ; j ③ Find the subinterval which contains x (i. e. find the corresponding j ); ④ Approximate f(x) by S (x). j ① 11/12

Chapter 3 Interpolation and Polynomial Approximation -- Cubic Spline Interpolation Lab 06. Cubic Spline Time Limit: 1 second; Points: 4 Construct the cubic spline interpolant S for the function f, defined at points x 0 < x 1 < … < xn, satisfying some given boundary conditions. Partition an given interval into m equallength subintervals, and approximate the function values at the endpoints of these subintervals. 12/12