Chapter 3 Interpolation and Polynomial Approximation If a

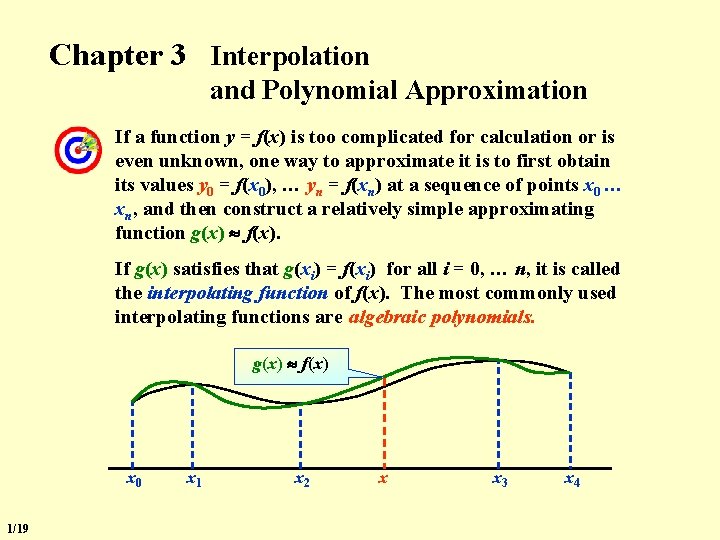
Chapter 3 Interpolation and Polynomial Approximation If a function y = f(x) is too complicated for calculation or is even unknown, one way to approximate it is to first obtain its values y 0 = f(x 0), … yn = f(xn) at a sequence of points x 0 … xn, and then construct a relatively simple approximating function g(x) f(x). If g(x) satisfies that g(xi) = f(xi) for all i = 0, … n, it is called the interpolating function of f(x). The most commonly used interpolating functions are …? algebraic polynomials. g(x) f(x) x 0 1/19 x 1 x 2 x x 3 x 4

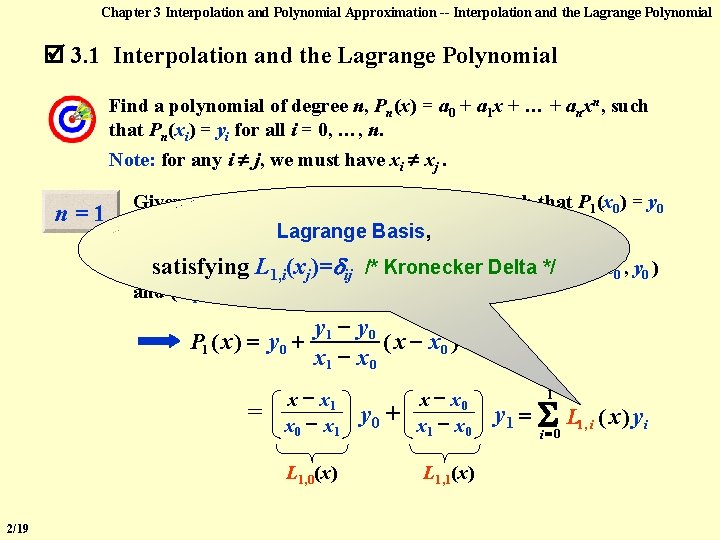
Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial 3. 1 Interpolation and the Lagrange Polynomial Find a polynomial of degree n, Pn(x) = a 0 + a 1 x + … + anxn, such that Pn(xi) = yi for all i = 0, …, n. Note: for any i j, we must have xi xj. n=1 Given x 0 , x 1; y 0 , y 1. Find P 1(x) = a 0 + a 1 x such that P 1(x 0) = y 0 and P 1(x 1) = y 1. Lagrange Basis, P 1 satisfying (x) is the line. Lfunction the two given ( x 0 , y 0 ) Deltapoints */ 1, i(xj)= through ij /* Kronecker and ( x 1, y 1 ). P 1 ( x ) = y 0 + = y 1 y 0 ( x x 0 ) x 1 x 0 x x 1 x 0 x 1 L 1, 0(x) 2/19 y 0 + x x 0 x 1 x 0 L 1, 1(x) 1 y 1 = L 1, i ( x ) y i i =0

Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial The mathematician S. had to move to a new place. His wife didn't trust him very much, so when they stood down on the street with all their things, she asked him to watch their ten trunks, while she got a taxi. Some minutes later she returned. Said the husband: "I thought you said there were ten trunks, but I've only counted to nine!" The wife said: "No, they're TEN!" "But I have counted them: 0, 1, 2, . . . " n 1 Ln, i(x ) Find Ln, i(x) for i = 0, …, n such that Ln, i(xj)= ij. Then let Pn ( x ) = n Ln, i(x) y. i=0 Hence Pn(xi) = yi. Each Ln, i has n roots x 0 … xi … xn n The n-th Lagrange Ln, i(x) = Ci ( x x 0 ). . . (x xi ). . . (x xn ) = Ci (x xj ) interpolating polynomial j i Ln, i ( xi ) = 1 3/19 i Ci = 1 j i ( xi x j ) j =0

Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial Theorem: If x 0, x 1, …, xn are n + 1 distinct numbers and f is a function whose values are given at these numbers, then the n-th Lagrange interpolating polynomial is unique. Proof: If not… Then there exists two polynomials Pn(x) and Qn(x) both satisfying the interpolating conditions. D(x) = Pn(x) – Qn(x) is a polynomial of degree n Yet D(x) has n + 1 distinct roots x 0, x 1, …, xn. Note: The interpolating polynomial is NOT unique unless its degree is constrained to be no greater than n. A counterexample is where p(x) can be a polynomial of any degree. 4/19

Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial Analyze the Remainder and f Cn + 1[a, b]. Suppose Consider the truncation error n = Rnsmooth ( x) K (with x) ((xx ) =xi ) (x ) = 0, Rn(x) has at least If n+1 Rolle’s Theorem: (x)roots is sufficiently 0 1 i =0 then therex exists all(xi 0=, 0, x 1)…, such ’(the ) =function 0. Fix any xi for n. that Define g for t in [a, b] by n In general, if (x 0 g(t) ) = = (x. R ) = (x ) = 0 1 2 K ( x ) (t xi ) i = 0 that such There exist g(x) has n+2 distinct roots x 0 … xn x such that There exists n (t ) f (n +1) ( x ) P(nn +1) ( x ) K ( x )( n + 1) ! = Rn( n 1 ) ( x ) - K ( x ) ( n + 1) ! ( n +1 ) Theref exists ( x ) K ( x) = 5/19 ( n + 1) ! + such that

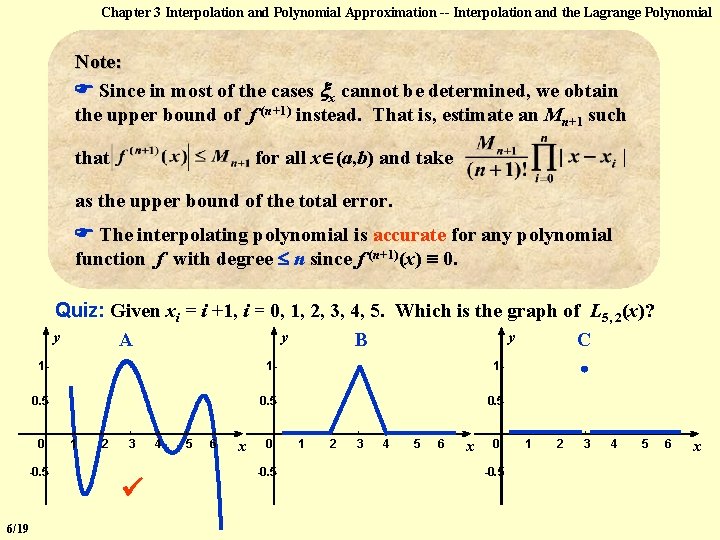
Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial Note: Since in most of the cases x cannot be determined, we obtain the upper bound of f (n+1) instead. That is, estimate an Mn+1 such that for all x (a, b) and take as the upper bound of the total error. The interpolating polynomial is accurate for any polynomial function f with degree n since f (n+1)(x) 0. Quiz: Given xi = i +1, i = 0, 1, 2, 3, 4, 5. Which is the graph of L 5, 2(x)? y y y A B C 1 - 1 - 1 - 0. 5 - 0 -0. 5 - 6/19 1 2 3 4 5 6 x 0 -0. 5 - 1 2 3 4 5 6 x

Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial Example: Suppose a table is to be prepared for the function f(x) = ex for x in [0, 1]. Assume that each entry of the table is accurate up to 8 decimal places and the step size is h. What should h be for linear interpolation to give an absolute error of at most 10– 6 ? Solution: Suppose that [0, 1] is partitioned into n equal-spaced subintervals [x 0, x 1], [x 1, x 2], …, [xn– 1 , xn], and x is in the interval [xk, xk+1]. Then the error estimation gives h 1. 72 10– 3 Simply take n = 1000 and h = 0. 001. 7/19

Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial Example: Given Use the linear and the quadratic Lagrange polynomial of sin x to compute sin 50 and then estimate the errors. Solution: First use x 0, x 1 and x 1, x 2 to compute the linear interpolations. Use p sin 50 0 P 1 ( 5 ) 0. 77614 18 Here In general, interpolation is better than extrapolation. and sin 50 = 0. 7660444… Error of extrapolation 0. 01001 Use sin 50 0. 76008, Error of interpolation 0. 00596 8/19

Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial Now use x 0, x 1 and x 2 to compute the quadratic interpolation. p sin 50 0 P 2 ( 5 ) 0. 76543 18 sin 50 = 0. 7660444… Error of the quadratic interpolation 0. 00061 Interpolation with higher degree usually obtain better results. The higher the better? Nooooooo…. 9/19

Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial When start writing the program, Oh yeah? What ifall I find Right. you Then you will find how easy it iswant to calculate Then you might to take the. Lagrange current interpolation the basis, L (x) , Excellent point ! n, i theinterpolating Lagrange polynomial. more points into account. not accurate enough? will have to look be re-calculated. Let’s at Neville’s Method… 10/19

Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial Definition: Let f be a function defined at x 0, x 1, …, xn, and suppose that m 1, …, mk are k distinct integers with 0 mi n for each i. The Lagrange polynomial that agrees with f(x) at the k points denoted by Theorem: Let f be defined at x 0, x 1, …, xk, and let xi and xj be two distinct numbers in this set. Then describes the k-th Lagrange polynomial that interpolates f at the k+1 points x 0, x 1, …, xk. Proof: For any 0 r k and r i and j, the two interpolating polynomials on the numerator are equal to f(xr) at xr , so P(xr) = f(xr). The first polynomials on the numerator equals f(xi) at xi , while the second term is zero, so P(xi) = f(xi). Similarly P(xj) = f(xj). The k-th Lagrange polynomial that interpolates f at the k+1 points x 0, x 1, …, xk is unique. 11/19

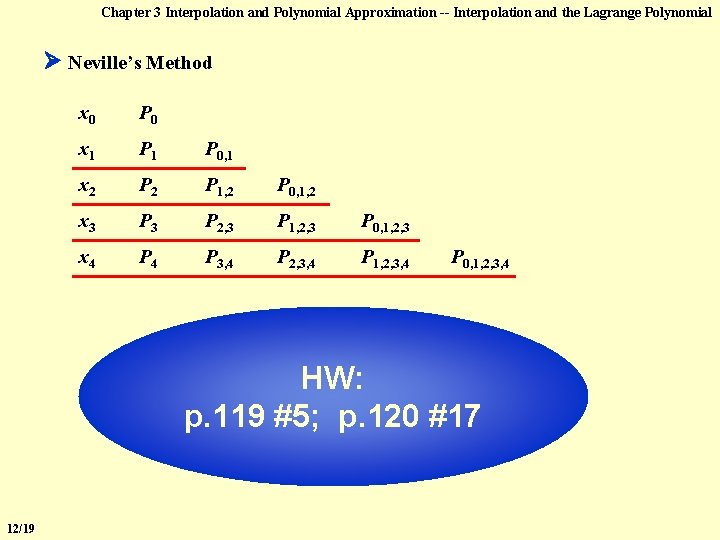
Chapter 3 Interpolation and Polynomial Approximation -- Interpolation and the Lagrange Polynomial Neville’s Method x 0 P 0 x 1 P 0, 1 x 2 P 1, 2 P 0, 1, 2 x 3 P 2, 3 P 1, 2, 3 P 0, 1, 2, 3 x 4 P 3, 4 P 2, 3, 4 P 1, 2, 3, 4 P 0, 1, 2, 3, 4 HW: p. 119 #5; p. 120 #17 12/19

Chapter 3 Interpolation and Polynomial Approximation -- Divided Differences 3. 2 Divided Differences The 1 st divided difference of f w. r. t. xi and xj The 2 nd divided difference of f w. r. t. xi , xj and xk The k+1 st divided difference of f w. r. t. x 0 … xk+1 f [ x 0 , x 1 , . . . , xk ] f [ x 1 , . . . , xk +1 ] f [ x 0 , . . . , xk +1 ] = x 0 x k +1 f [ x 0 , . . . , xk 1 , xk ] f [ x 0 , . . . , xk 1 , xk +1 ] = x k +1 13/19

Chapter 3 Interpolation and Polynomial Approximation -- Divided Differences As a matter of fact, where Warning: my head is exploding… What is the point of this formula? The value of f [ x 0, …, xk ] is independent of the order of the numbers x 0, …, xk. 14/19

Chapter 3 Interpolation and Polynomial Approximation -- Divided Differences Newton’s Interpolation 1 2 ………… n 1 1 + (x x 0) 2 Nn(x) 15/19 + … … + (x x 0)…(x xn 1) ai = f [ x 0, …, xi ] n 1 Rn(x)

Chapter 3 Interpolation and Polynomial Approximation -- Divided Differences Note: Since the n-th interpolating polynomial is unique, Nn(x) Pn(x). They must have the same truncation error. That is, The procedure is similar to Neville’s method. f (x 0) f (x 1) f (x 2) … f (xn 1) f (xn+1) 16/19 f [x 0, x 1] f [x 1, x 2] …… …… f [xn 1, xn] f [xn, xn+1] f [x 0, x 1 , x 2] …… …… f [xn 2, xn 1, xn] f [xn 1, xn+1] f [x 0, …, xn] f [x 1, …, xn+1] f [x 0, …, xn+1]

Chapter 3 Interpolation and Polynomial Approximation -- Divided Differences Formulae with Equal Spacing If the points are equally spaced: forward difference backward difference centered difference 17/19 f i = f i +1 f i k 1 f i = ( k f i ) = k 1 f i + 1 k 1 f i = f i 1 k fi = k 1 f i 1 其中

Chapter 3 Interpolation and Polynomial Approximation -- Divided Differences Some important properties Linearity: If f (x) is a polynomial of degree m , then polynomial of degree m – k and The values of the differences can be obtained from the function n f k = ( 1) f n+ k j j j=0 n n j where And n f k = ( 1) n j =0 n j n f k + j n j /* binomial coefficients */ n vice-versa f [ x 0 , . . . , x k ] = f n + k = nj j f k j =0 From Rn k f 0 k! hk f [ xn , xn 1 , . . . , xn k ] = 18/19 is a fn k ! hk k f (k ) k f 0 ( ) = k h

Chapter 3 Interpolation and Polynomial Approximation -- Divided Differences Newton’s formulae Newton’s forward-difference formula Let , then N n ( x ) = N n ( x 0 + t h ) = n k =0 t k f ( x 0 ) k HW: p. 131 #5(a)(b); Newton’s backward-difference formula p. 132 #13 Reverse the order of the points Let 19/19 n t k =0 k k , then N n ( x ) = N n ( xn + t h) = ( 1) k f ( xn )