Polynomial Interpolation and Extrapolation Marija Stanojevic SI 20100011

Polynomial Interpolation and Extrapolation Marija Stanojevic SI 2010/0011

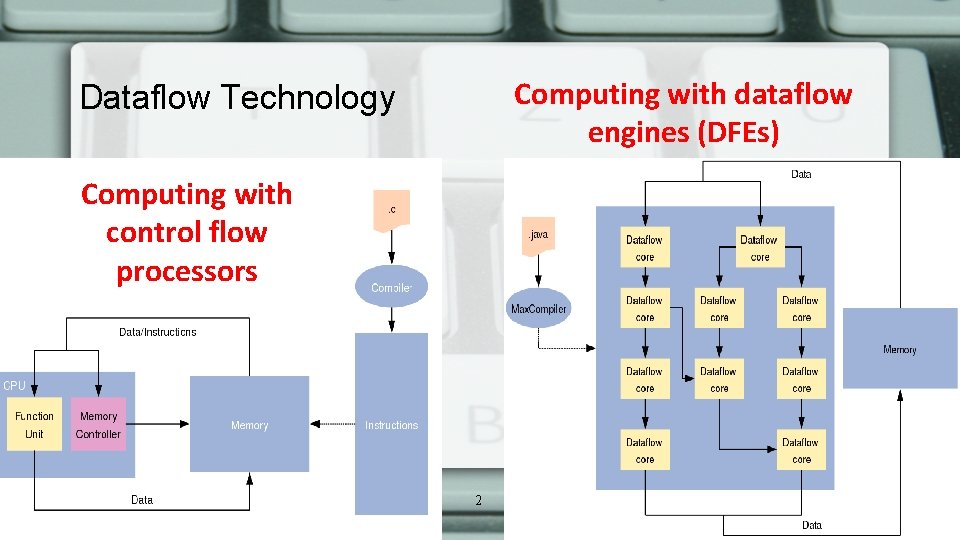
Computing with dataflow engines (DFEs) Dataflow Technology Computing with control flow processors 2

Maxeler Technology MAXELER DATAFLOW COMPUTING One result per clock cycle Engine is written in Java and Host is written in C. Minimal frequency f achieves maximal performance, thus for a given power budget, we get Maximum Performance Computing (MPC)! 3 3 /16

Neville's algorithm Given a set of n+1 data points (xi, yi) where no two xi are the same, the interpolating polynomial is the polynomial p of degree at most n with the property: p(xi) = yi for all i = 0, …, n This polynomial exists and it is unique. Neville's algorithm evaluates this polynomial at some point and gives value y and error estimate dy It is easy to work with algorithm recursively as shown in figure in the right bottom corner 4

Neville's algorithm Algorithm is based on formula: It can be easily become recursive algorithm by next transformations: 5

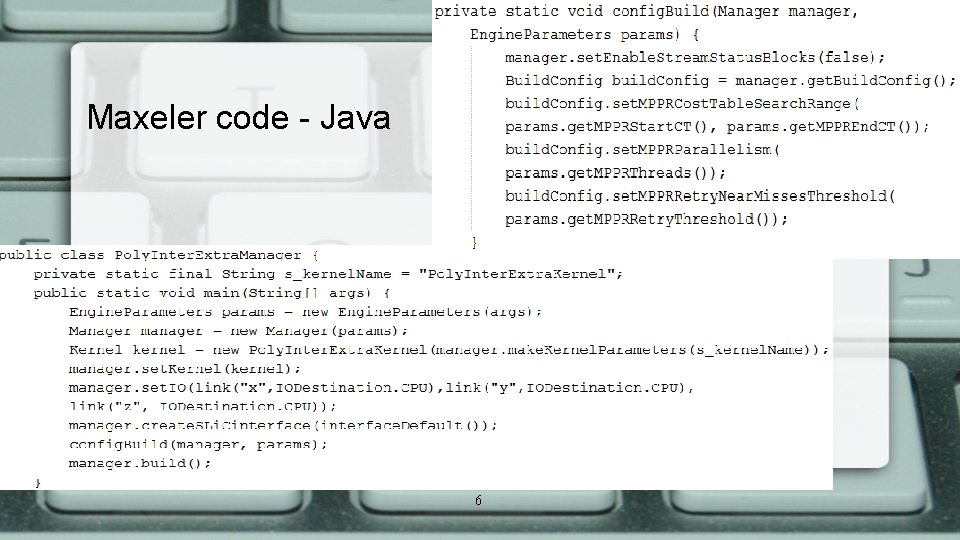
Maxeler code - Java 6

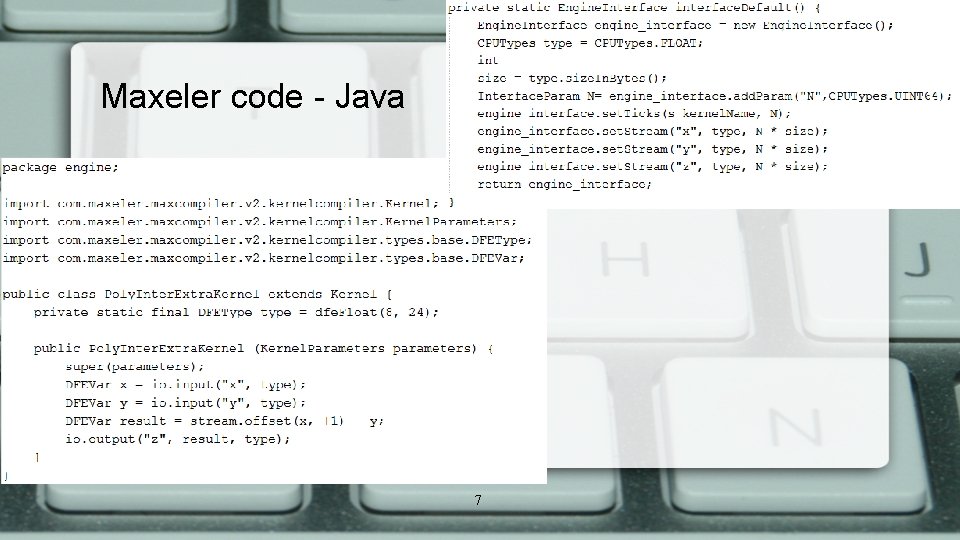
Maxeler code - Java 7

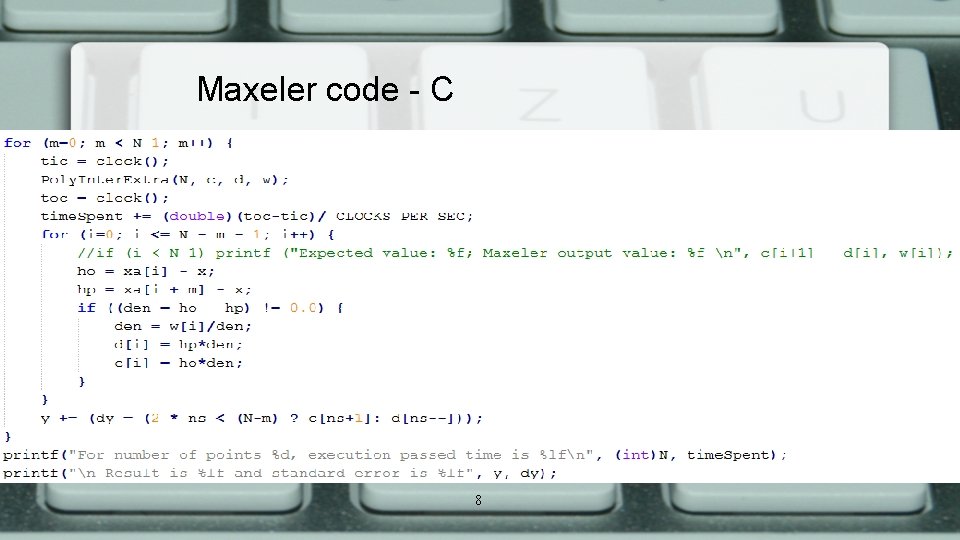
Maxeler code - C 8

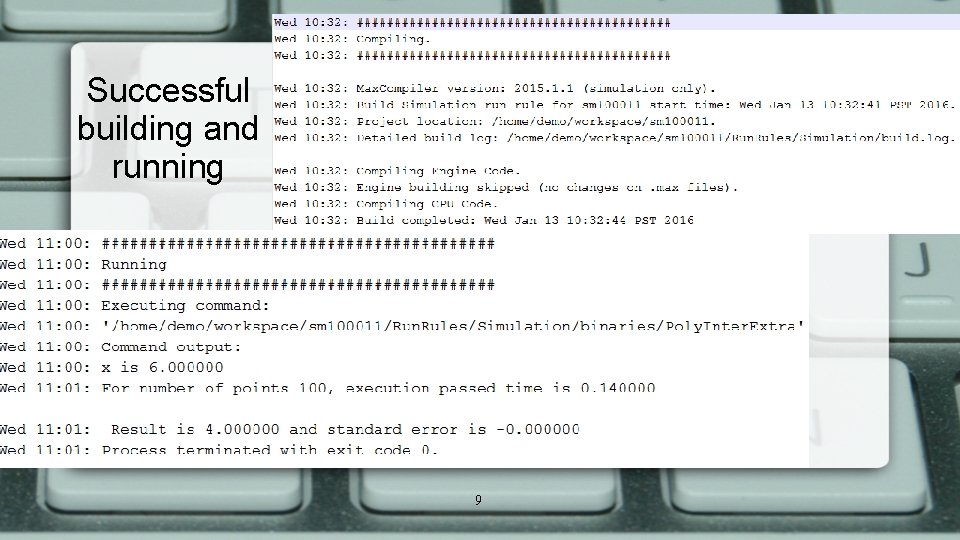
Successful building and running 9

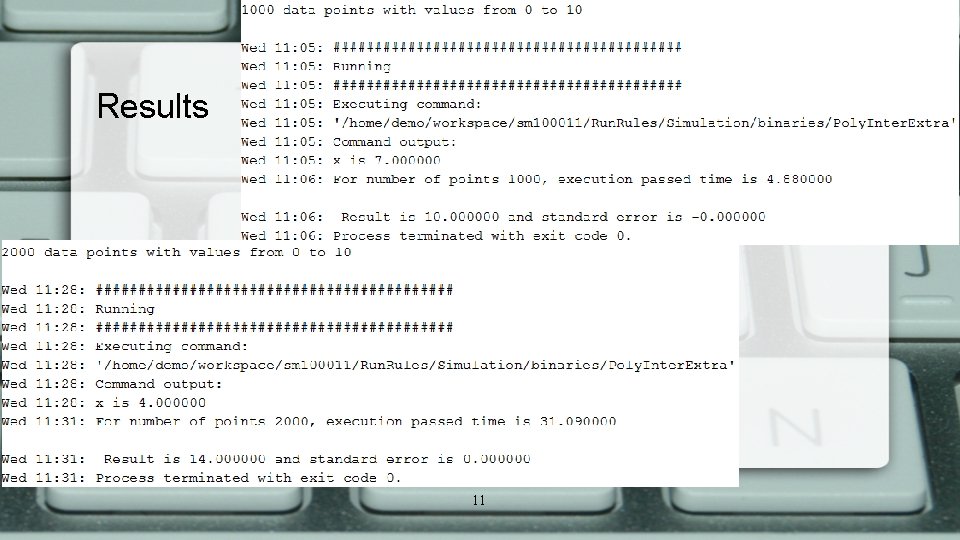
Results X and Y coordinates of points were in range from 0 to 10 Algorithm complexity is N 2 Interpolation is done for: – 4 points with time of execution on Maxeler: 0. 01 s – 100 points with time of execution on Maxeler: 0. 14 s – 1000 points with time of execution on Maxeler: 4. 68 s – 2000 points with time of execution on Maxeler: 31. 09 s 10

Results 11

Conclusion This project implements Neville's interpolation algorithm on Maxeler Whole project code can be found on: https: //github. com/mstanojevic 118/Maxeler. Project There are two versions of C code for Maxeler; File with Nice. Output in name gives nicer, but less extensive output Maxeler is practical for big amount of data, because it's fast and energy saving 12

References Milutinovic V. , Rakocevic G. , Stojanovic S. , Sustran Z. , Mencer O. , Pell O. , Flynn M. , Korolija N. , Data. Flow Exa. Scale Super. Computing: Revisiting the Paradigm and the Algorithms, https: //www. bsc. es/sites/default/files/public/ mare_nostrum/hpc-events/hpcac 2012 -12_maxeler. pdf Selected Max. Compiler Examples, Sustran Z. , Stojanovic S. , home. etf. rs/~vm/tutorial/Berlin/11. %20 Maxeler-examples. pptx Press W. , Teukolsky S. , Vetterling W. , Flannery B. , Numerical Receipes in C, Cambridge University Press, 2002 Neville's algorithm, https: //en. wikipedia. org/wiki/Neville%27 s_algorithm 13

Thank you for your attention! 14