Agenda 1 Dimension reduction 1 Principal component analysis

Agenda 1. Dimension reduction 1. Principal component analysis (PCA) 2. Multi-dimensional scaling (MDS) 2. Microarray visualization

Why Dimension Reduction • Computation: The complexity grows exponentially with the dimension. • Visualization: projection of highdimensional data to 2 D or 3 D. • Interpretation: the intrinsic dimension maybe small.

1. Dimension reduction 1. Principal component analysis (PCA) 2. Multi-dimensional Scaling (MDS)

Philosophy of PCA • A PCA is concerned with explaining the variance-covariance sturcture of a set of variables through a few linear combinations. • We typically have a data matrix of n observations on p correlated variables x 1, x 2, …xp • PCA looks for a transformation of the xi into p new variables yi that are uncorrelated. • Want to present x 1, x 2, …xp with a few yi’s without lossing much information.

PCA • Looking for a transformation of the data matrix X (nxp) such that • Y= T X= 1 X 1+ 2 X 2+. . + p Xp • Where =( 1 , 2 , . . , p)T is a column vector of wheights with 1²+ 2²+. . + p² =1

• Maximize the variance of the projection of the observations on the Y variables • Find so that Var( T X)= T Var(X) is maximal • Var(X) is the covariance matrix of the Xi variables

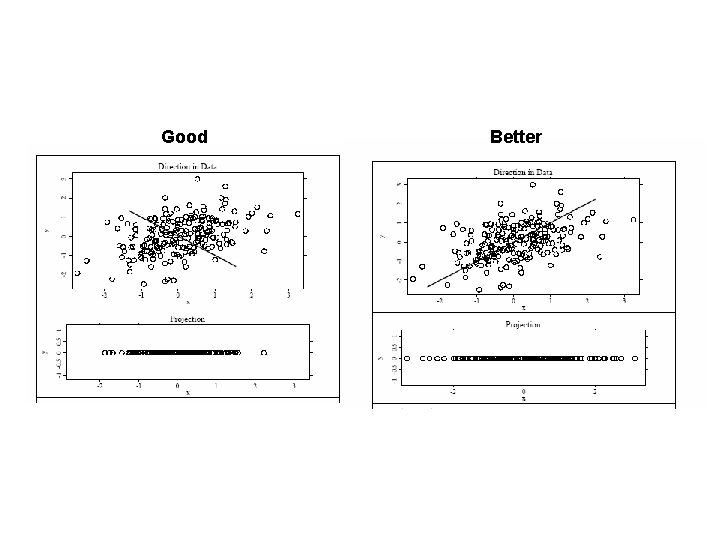
Good Better

Eigen Vector and Eigen Value

PCA

Covariance matrix

And so. . We find that • The direction of is given by the eigenvector 1 correponding to the largest eigenvalue of matrix Σ. • The second vector that is orthogonal (uncorrelated) to the first is the one that has the second highest variance which comes to be the eignevector corresponding to the second eigenvalue • And so on …

So PCA gives • New variables Yi that are linear combination of the original variables (xi): • Yi= ei 1 x 1+ei 2 x 2+…eipxp ; i=1. . p • The new variables Yi are derived in decreasing order of importance; • they are called ‘principal components’

Scale before PCA • PCA is sensitive to scale • PCA should be applied on data that have approximately the same scale in each variable

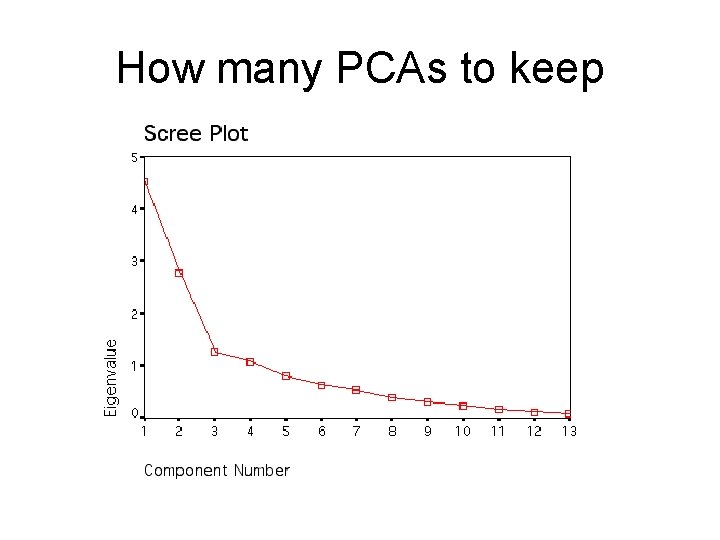
How many PCAs to keep

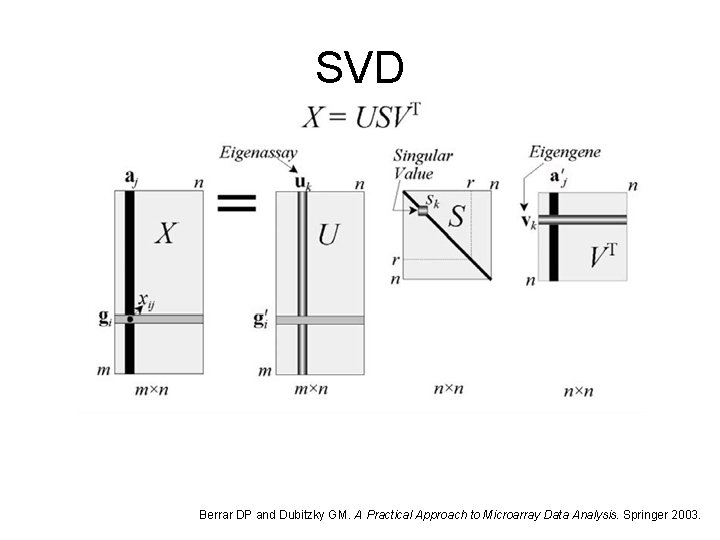
SVD (singular value decomposition)

SVD Berrar DP and Dubitzky GM. A Practical Approach to Microarray Data Analysis. Springer 2003.

SVD and PCA

PCA application: genomic study • Population stratification: allele frequency differences between cases and controls due to systematic ancestry differences— can cause spurious associations in disease studies. • PCA could be used to infer underlying population structure.

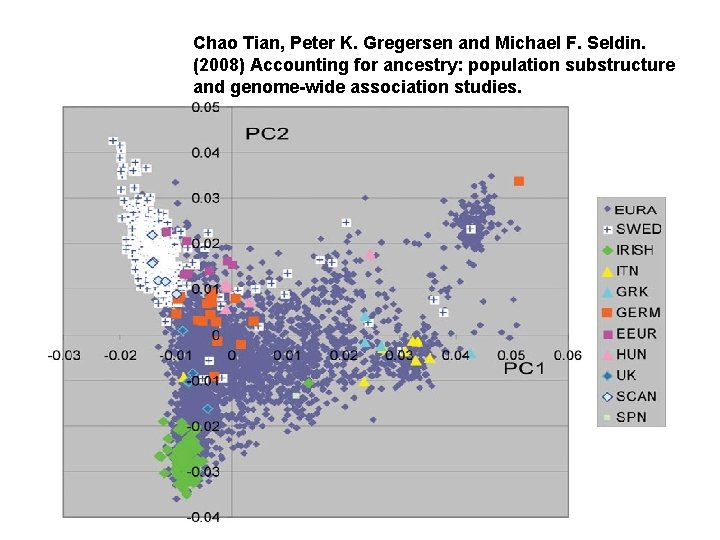
Figure 2 Nature Genetics 38, 904 - 909 (2006) Principal components analysis corrects for stratification in genome-wide association studies Alkes L Price, Nick J Patterson, Robert M Plenge, Michael E Weinblatt, Nancy A Shadick & David Reic

Chao Tian, Peter K. Gregersen and Michael F. Seldin. (2008) Accounting for ancestry: population substructure and genome-wide association studies.

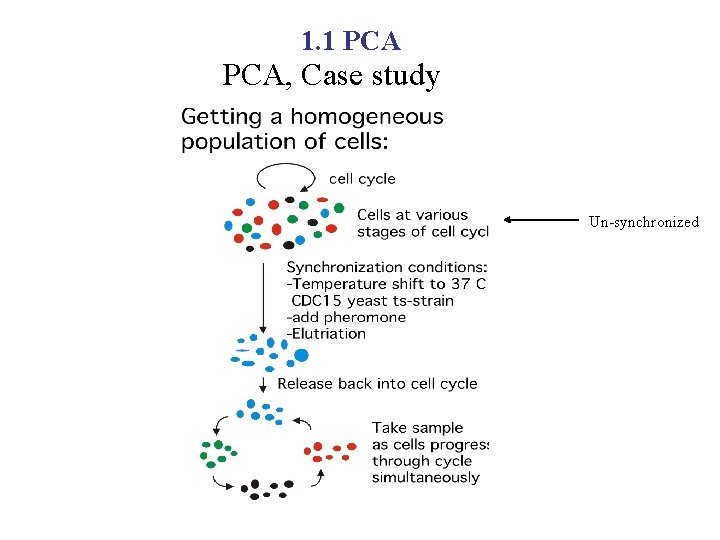
1. 1 PCA, Case study Transcriptional regulation and function during the human cell cycle, Cho et al. (2001) Nature Genetics Vol 27, 48 -54 -- to identify cell-cycle–regulated transcripts in human cells -- Primary fibroblasts prepared from human foreskin were grown to approximately 30% confluence and synchronized in late G 1 using a double thymidine-block protocol 9. Cultures were then released from arrest, and cells were collected every 2 hours for 24 hours, covering nearly 2 complete cell cycles. -- Messenger RNA was isolated, labeled and hybridized to sets of arrays containing probes for approximately 40, 000 human genes and nonoverlapping ESTs. We carried out the entire synchronization experiment in duplicate under identical conditions for 6, 800 genes on Affy array. The two data sets were averaged analyzed using both supervised and unsupervised clustering of expression patterns.

1. 1 PCA, Case study Un-synchronized

1. 1 PCA

1. 1 PCA projection: 387 genes in 13 -dim space (time points) are projected to 2 D space using correlation matrix; Gene phase 1: G 1; 4: S; 2: G 2; 3: M

1. 1 PCA Variance in data explained by the first n principle components

1. 1 PCA The weights of the 13 principle directions

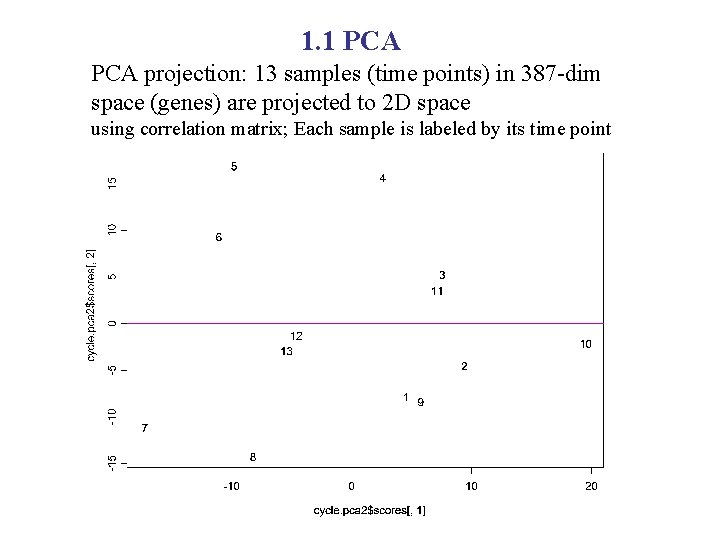
1. 1 PCA projection: 13 samples (time points) in 387 -dim space (genes) are projected to 2 D space using correlation matrix; Each sample is labeled by its time point

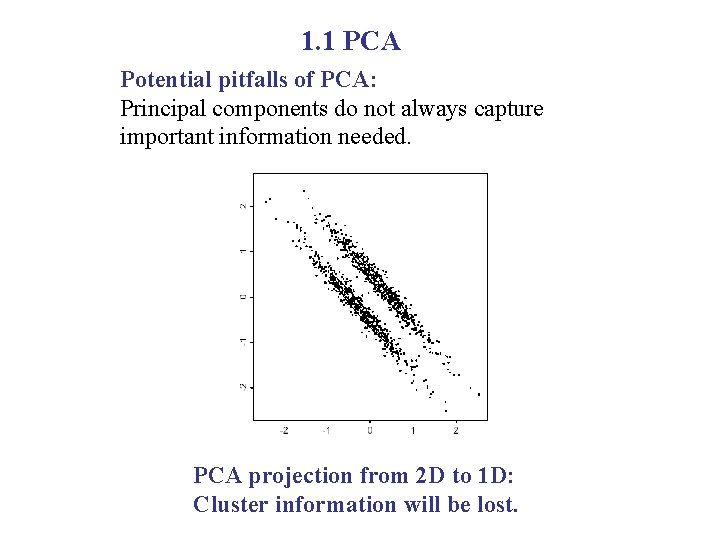
1. 1 PCA Potential pitfalls of PCA: Principal components do not always capture important information needed. PCA projection from 2 D to 1 D: Cluster information will be lost.

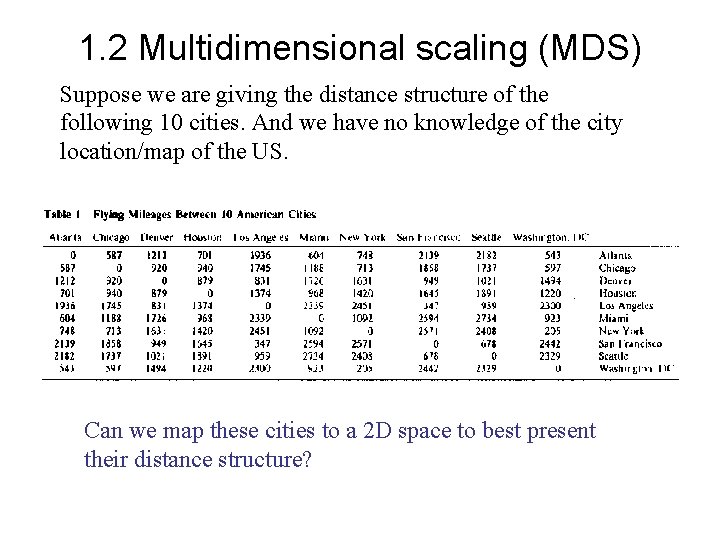
1. 2 Multidimensional scaling (MDS) Suppose we are giving the distance structure of the following 10 cities. And we have no knowledge of the city location/map of the US. Can we map these cities to a 2 D space to best present their distance structure?

1. 2 Multidimensional scaling (MDS) • MDS deals with the following problem: for a set of observed similarities (or distances) between every pair of N items, find a representation of the items in few dimensions such that the interitem proximities “nearly match” the original similarities (or distance). • The numerical measure of how close the original distances and the distances at lower dimensional coordinate is called stress.

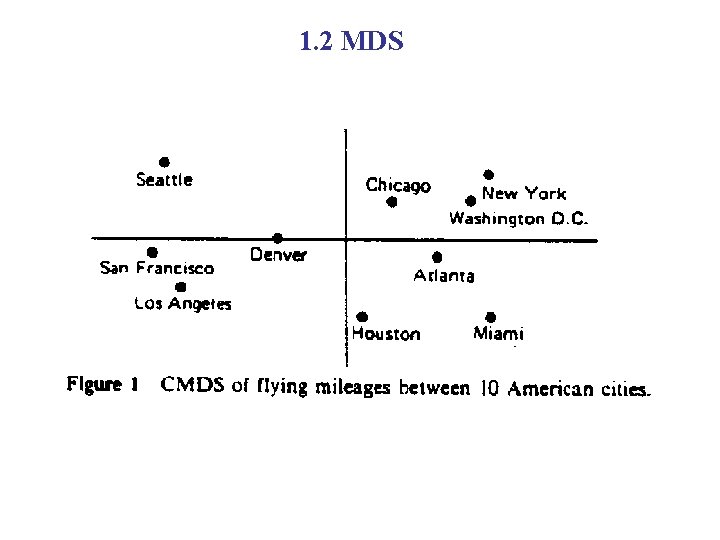
1. 2 MDS

1. 2 MDS

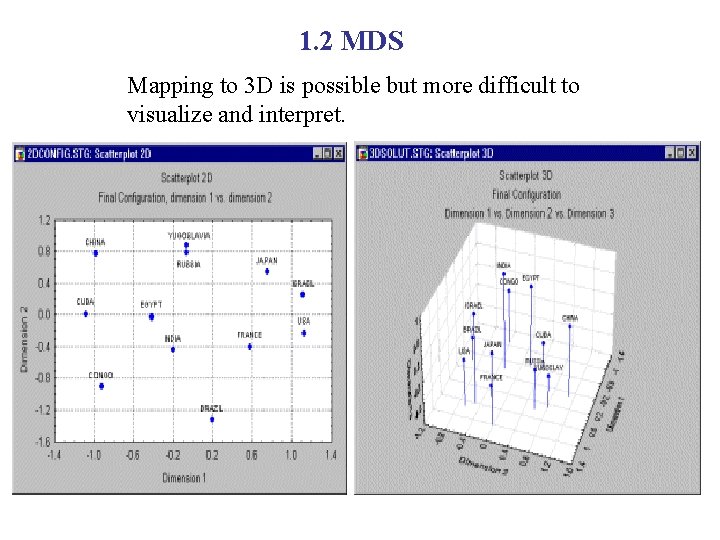
1. 2 MDS Mapping to 3 D is possible but more difficult to visualize and interpret.

1. 2 MDS 1. MDS attempts to map objects to a visible 2 D or 3 D Euclidean space. The goal is to best preserve the distance structure after the mapping. 2. The original data can be of high-dimensional or even non-metric space. The method only cares the distance (dissimilarity) structure. 3. The resulting mapping is not unique. Any rotation or reflection of a mapping solution is also a solution. 4. It could be shown that the results of PCA are exactly those of classical MDS if the distances calculated from the data matrix are Euclidean.

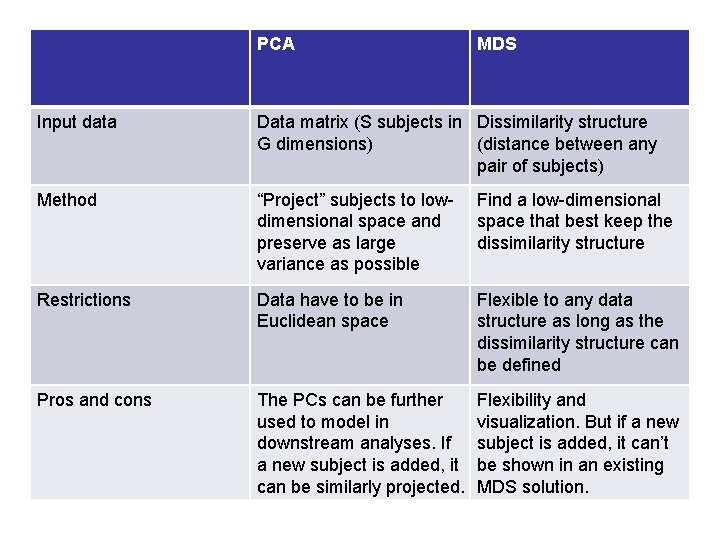
PCA MDS Input data Data matrix (S subjects in Dissimilarity structure G dimensions) (distance between any pair of subjects) Method “Project” subjects to lowdimensional space and preserve as large variance as possible Find a low-dimensional space that best keep the dissimilarity structure Restrictions Data have to be in Euclidean space Flexible to any data structure as long as the dissimilarity structure can be defined Pros and cons The PCs can be further used to model in downstream analyses. If a new subject is added, it can be similarly projected. Flexibility and visualization. But if a new subject is added, it can’t be shown in an existing MDS solution.

2. Microarray visualization Data matrix Data: X={xij}n d , an n (genes) d (samples) matrix.

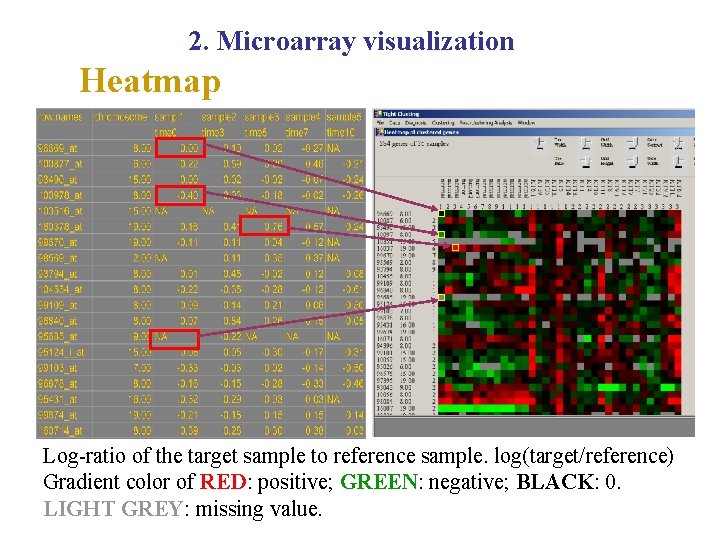
2. Microarray visualization Heatmap Log-ratio of the target sample to reference sample. log(target/reference) Gradient color of RED: positive; GREEN: negative; BLACK: 0. LIGHT GREY: missing value.

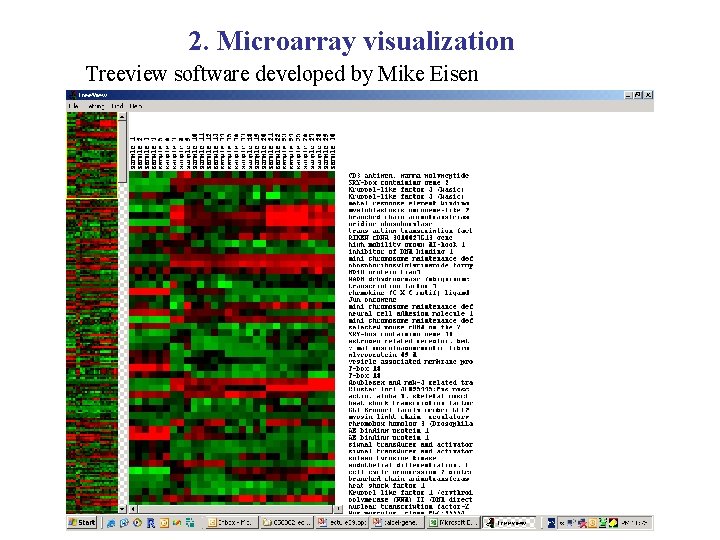
2. Microarray visualization Treeview software developed by Mike Eisen

3. Software for dimension reduction & visualization PCA in R: prcomp(stats) princomp(stats) screeplot(stats) Principal Components Analysis (preferred) Principal Components Analysis Screeplot of PCA Results PCA in IMSL (a commercial C library) MDS in R: iso. MDS(MASS) cmdscale(stats) sammon(MASS) Kruskal's Non-metric Multidimensional Scaling Classical (Metric) Multidimensional Scaling Sammon's Non-Linear Mapping MDS: Various software and resources about MDS http: //www. granular. com/MDS/ Heatmap visualization: Treeview http: //rana. lbl. gov/Eisen. Software. htm