Outline dimension reduction methods Linear dimension reduction Nonlinear

Outline • • • dimension reduction methods Linear dimension reduction Nonlinear dimension reduction Graph-based dimension reduction Applications

Dimension reduction features A 1 A 2 A 3 … C B 1 10 Y : Y 21 N : N 13 Y : Y 14 N : N 15 Y : Y 10 Y : : : objects … … dimenion reduction (차원감소) • feature extraction (특징추출) • feature selection (특징선택) • dimension: the number of features B 2 … C

Dimension reduction • Reduce the dimensionality of high dimensional data • Identify new meaningful underlying features • The computational overhead of the subsequent processing stages is reduced • Reduce noise effects • Visualization of the data

Dimension reduction methods • • PCA(principal component analysis) LDA(Linear discriminant analysis) LLE(Locally linear embedding) Isomap LPP(Locality preserving projection) UDP(Unsupervised discriminant projection) Kernel based nonlinear dimension reduction …….

Linear dimension reduction m R a W: a matrix of size mxp (p << m) p R t Wa § How to find p column vectors of W? - use a training data set - what is objective criteria? § Traditional linear dimension reduction methods - PCA(principal component analysis) - LDA(Linear discriminant analysis) =

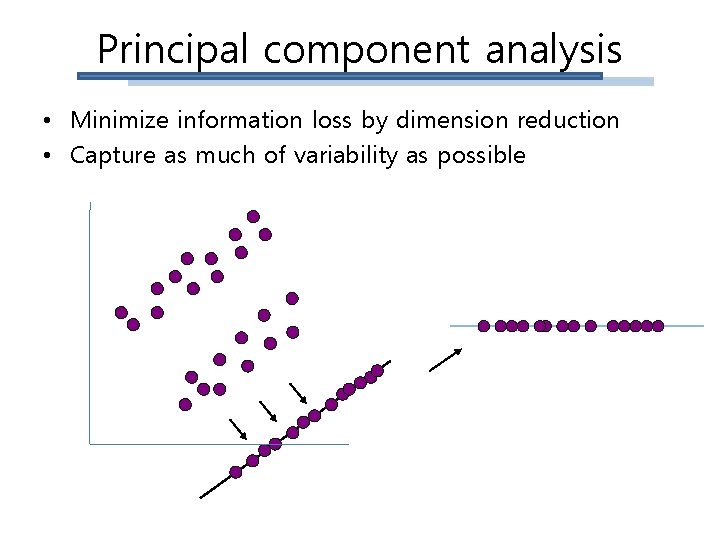
Principal component analysis • Minimize information loss by dimension reduction • Capture as much of variability as possible

PCA (or Karhunen-Loéve transform) § given data set {a 1, ┉, an } , centroid § total scatter matrix § Find a projection vector w to maximize § Find the eigenvector w corresponding to the largest eigenvalue of St : § eigenvectors w 1 , … , wp corresponding to the p largest eigenvalues of St -> reduction to p-dimensional space

Linear Discriminant analysis(LDA) • PCA seeks directions which are efficient for representing data • LDA seeks direction which are useful for discriminating between data in different classes

LDA § given data set {a 1, ┉, an } with class label information , global centroid § § class centroid Within-class scatter matrix Between-class scatter matrix Maximize between-class scatter and minimize within-class scatter Solve the generalized eigenvalue problem

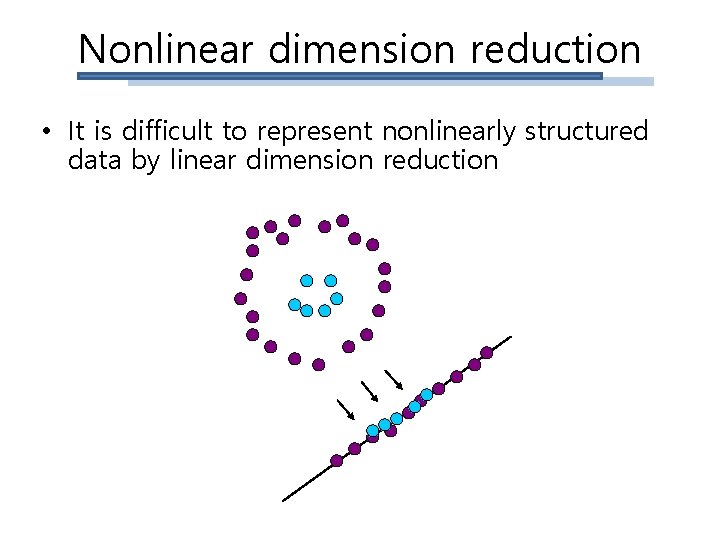
Nonlinear dimension reduction • It is difficult to represent nonlinearly structured data by linear dimension reduction

Locally linear embedding(LLE) • Expectation: each data point and its neighbors lie on a locally linear patch of the manifold • [reference] Nonlinear dimensionality reduction by locally linear embedding, A. T. Roweis and L. K. Saul, Science, vol. 290, pp. 2323 -2326, 2000

LLE • Algorithm 1. Find the nearest neighbors of each data point 2. Express each data point xi as a linear combination of its neighbors wij = 0 if xj is not a near neighbor of xi 3. Find the coordinates yi of each point xi in lowerdimensional space by using the weights wij found in step 2 minimize

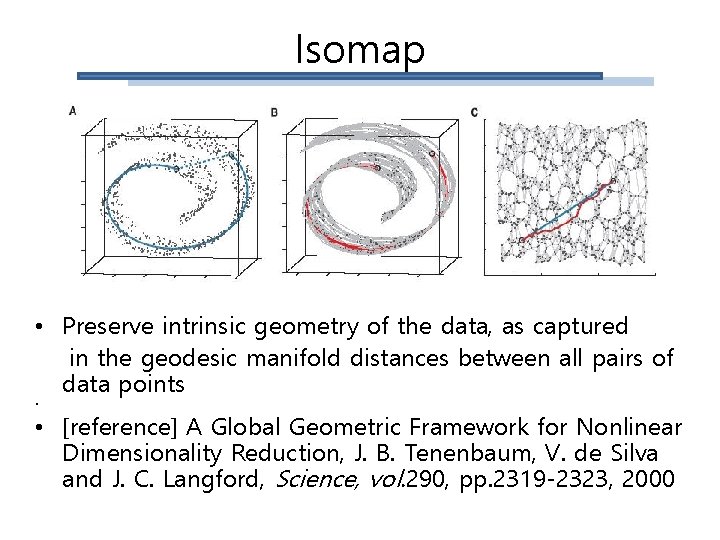
Isomap • Preserve intrinsic geometry of the data, as captured in the geodesic manifold distances between all pairs of data points • • [reference] A Global Geometric Framework for Nonlinear Dimensionality Reduction, J. B. Tenenbaum, V. de Silva and J. C. Langford, Science, vol. 290, pp. 2319 -2323, 2000

Isomap • Algorithm 1. Find the nearest neighbors of each data point and create a weighted graph by connecting a point to its nearest neighbors 2. Redefine the distances between points to be the length of the shortest path between the two points 3. Apply classical MDS(Multidimensional scaling)

Example by Isomap

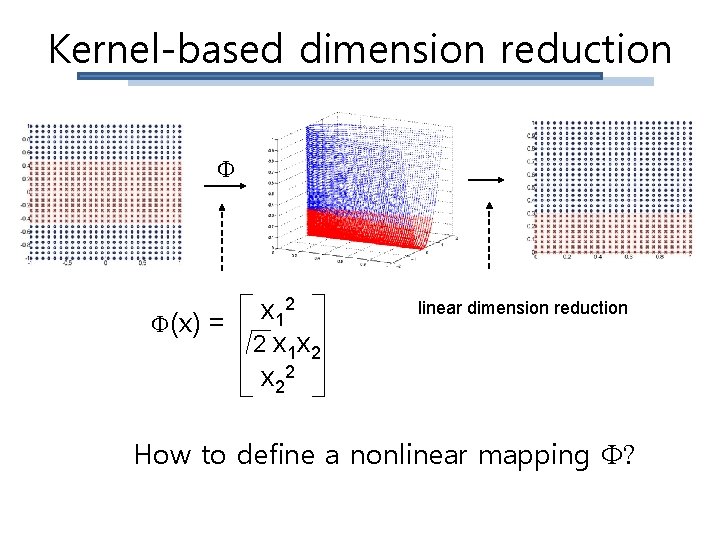
Kernel-based dimension reduction 2 x 1 (x) = 2 x 1 x 2 x 22 linear dimension reduction How to define a nonlinear mapping ?

Kernel methods § If a kernel function k(x, y) satisfies Mercer’s condition, then there exists a mapping A < x, y > (A) < (x), (y)>= k(x, y) • Gaussian kernel • • Polynomial kernel k(x, y) = ( <x, y>+ß )d § As long as an algorithm can be written in terms of inner products, it can be performed on the feature space

Nonlinear discriminant analysis § As long as an algorithm can be written in terms of inner products, it can be performed on the feature space § In LDA, § LDA written in terms of inner products

Graph-based dimension reduction • Graph G=<X, W> X={xi, 1 i n} : n nodes of data points W={ wij }1 i, j n : similarity (or weight) matrix W can be sparse by using -neighborhoods or k nearest neighbors for edge construction • Let yi be the embedding of xi • [LPP(Locality preserving projection)] ensures that if xi and xj are close then yi and yj are close as well minimize

Graph-based methods • Let yi be the embedding of xi minimize • Linearization: minimize • Using a penalty graph <X, P=(pij )> maximize

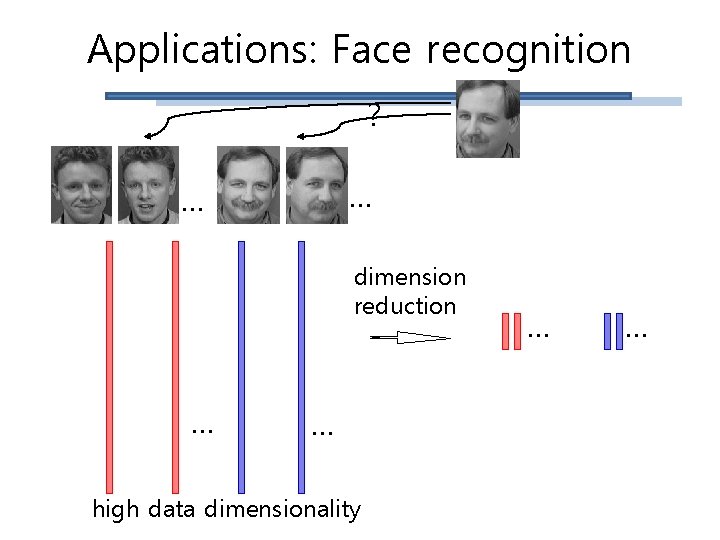
Applications: Face recognition ? … … dimension reduction … … high data dimensionality … …

Applications: text mining • Each document becomes a `term' vector, – each term is a component (attribute) of the vector, – the value of each component is the number of times the corresponding term occurs in the document. • Document data has high dimensionality

Reference • Introduction to data mining, P. Tan, M. Steinbach and V. Kumar, Addison Wesley, 2006 • Pattern classification, R. Duda, P. Hart and D. Stork, Wiley-interscience, 2001 • [LPP] Locality preserving projections, X. He and P. Niyogi, Proc. conf. Neural information processing systems, 2003 • Graph embedding and extensions: a general framework for dimensionality reduction, S. Yan, D. Xu, H. Zhang, Q. Yang and S. Lin, IEEE transactions on pattern analysis and machine intelligence, Vol. 29(1), 2007