A Yu Smirnov International Centre for Theoretical Physics

A. Yu. Smirnov International Centre for Theoretical Physics, Trieste, Italy Invisibles network INT Training lectures June 25 – 29, 2012

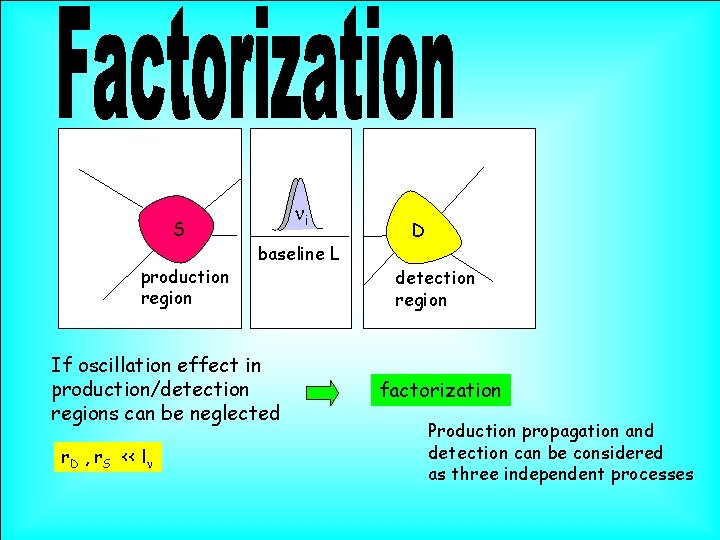
S production region ni baseline L If oscillation effect in production/detection regions can be neglected r. D , r. S << ln D detection region factorization Production propagation and detection can be considered as three independent processes

Amplitude of (survival) probability A(ne) = <ne|n (x, t)> = cos 2 q g 1(x – v 1 t) + sin 2 q g 2(x – v 2 t) e if Probability in the moment of time t + P(ne) = - dx |<ne|n (x, t)>|2 = interference = cos 4 q + sin 4 q + 2 sin 2 q cos f dx g 1(x – v 1 t) g 2(x – v 2 t) If dx| gk|2 = 1 If g 1 = g 2 P(ne) = 1 - 2 sin 2 q cos 2 q (1 - cos f) = 1 - sin 2 2 q sin 2 ½f 2 px Dm 2 x f= = ln 2 E ln = 4 p 2 E Dm Oscillation length depth of oscillations ! !

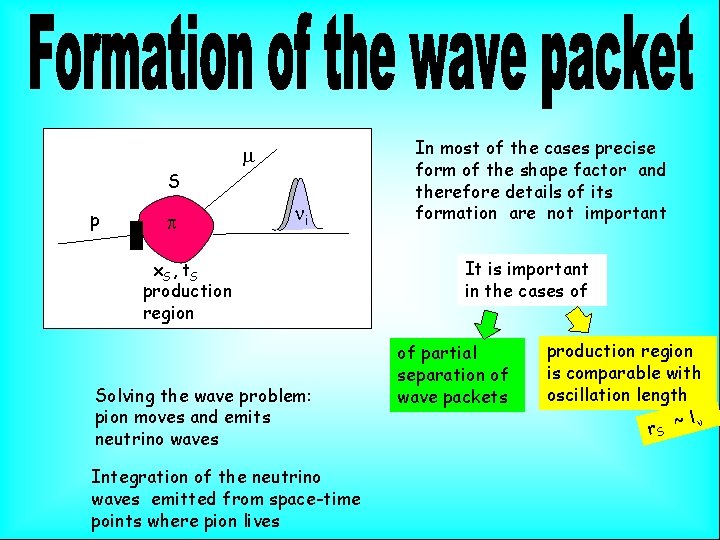
m S p p ni x S , t. S production region Solving the wave problem: pion moves and emits neutrino waves Integration of the neutrino waves emitted from space-time points where pion lives In most of the cases precise form of the shape factor and therefore details of its formation are not important It is important in the cases of of partial separation of wave packets production region is comparable with oscillation length l r. S ~ n

Pion decay: gi(x, t) e ifi ! E. Akhmedov, D. Hernandez, A. S. = dp dx. S dt. S M yp (x. S, t. S) ym (x. S, t. S) exp[ip ( x - x. S) – i. Ei (t – t. S)] integration over production region part of matrix element plane wave for neuutrino Pion wave function: y p (x. S, t. S) = exp[ –½Gt. S] gp(x. S, t. S) exp[ -ifp(x. S, t. S)] usually: gp(x. S, t. S) ~ d (x. S - vpt. S) Muon wave function: y m (x. S, t. S) = gm(x’ - x. S, t’ - t. S) exp[ ifm (x’ - x. S , t’ - t. S)] determined by detection of muon If muon is not detected: plane wave phase factor disappears from probability

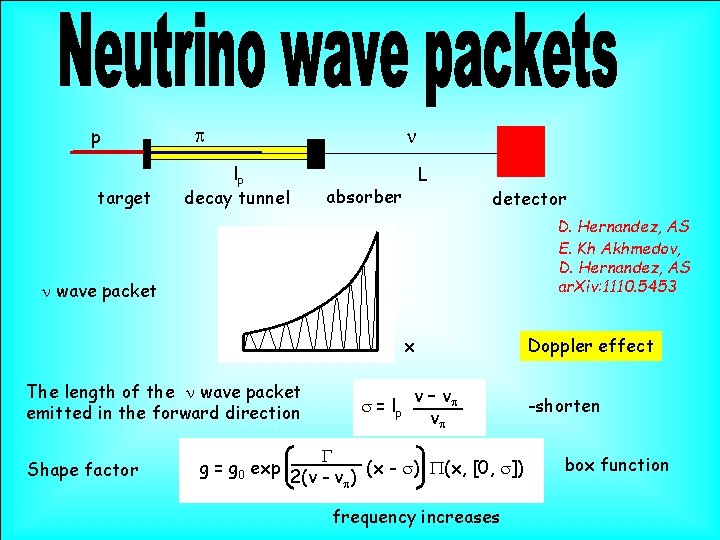
p target p n lp decay tunnel L absorber detector D. Hernandez, AS E. Kh Akhmedov, D. Hernandez, AS ar. Xiv: 1110. 5453 n wave packet x The length of the n wave packet emitted in the forward direction Shape factor g = g 0 exp s = lp v – vp vp G (x - s) P(x, [0, s]) 2(v - vp) frequency increases Doppler effect -shorten box function

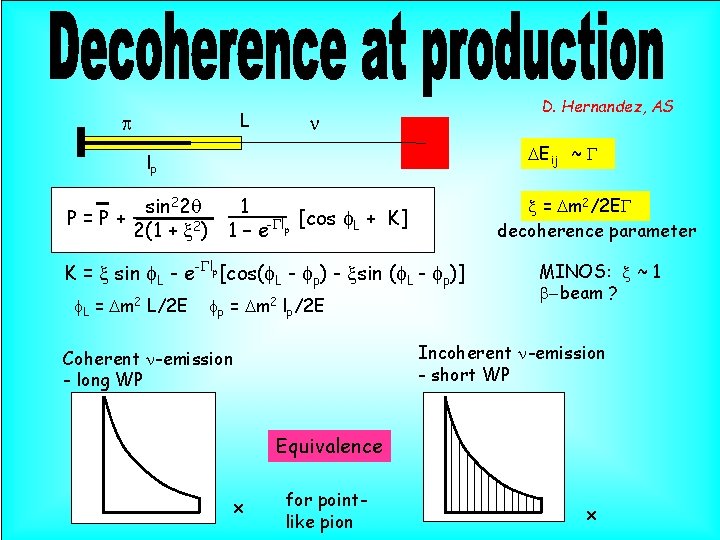
L p D. Hernandez, AS n DEij ~ G lp sin 22 q 1 P=P+ [cos f. L + K] 2(1 + x 2) 1 – e-Glp x = Dm 2/2 EG decoherence parameter K = x sin f. L - e-Glp[cos(f. L - fp) - xsin (f. L - fp)] f. L = Dm 2 L/2 E fp = Dm 2 lp/2 E MINOS: x ~ 1 b-beam ? Incoherent n-emission - short WP Coherent n-emission - long WP Equivalence x for pointlike pion x

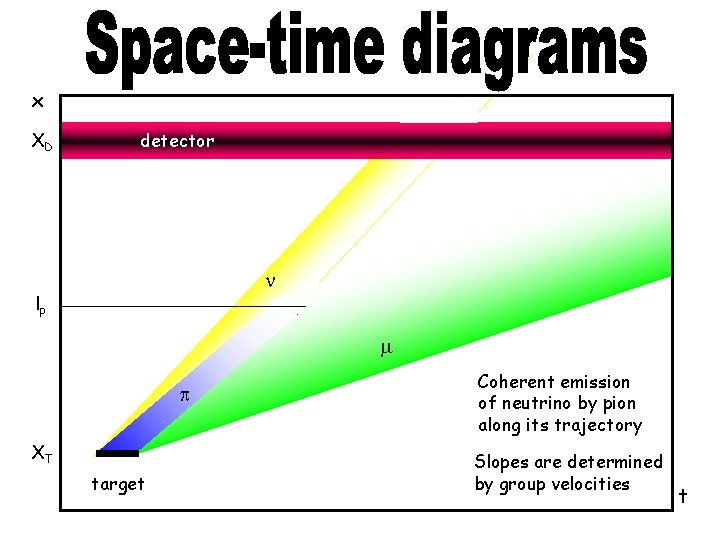
x XD detector n lp m p XT target pion Coherent emission of neutrino by pion along its trajectory Slopes are determined by group velocities t

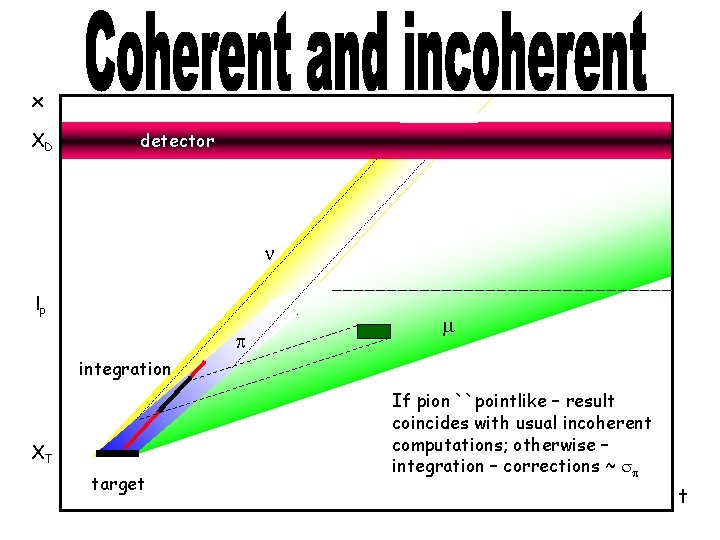
x XD detector n lp p integration XT target pion m If pion ``pointlike – result coincides with usual incoherent computations; otherwise – integration – corrections ~ sp t

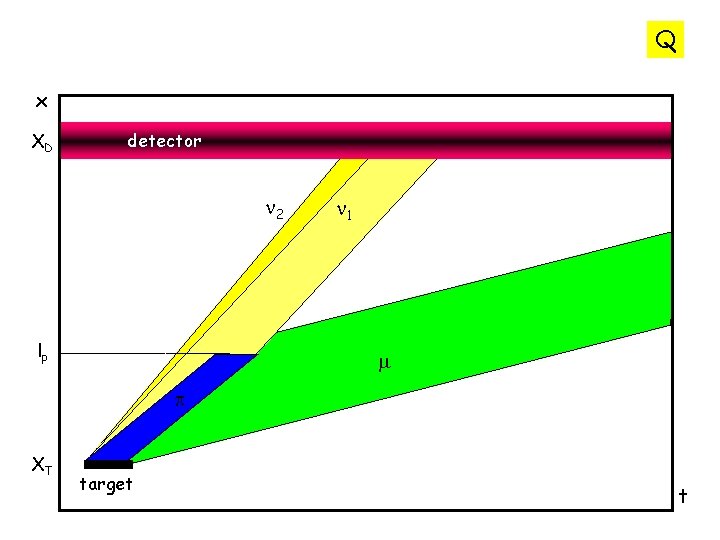
Q x XD detector n 2 lp p XT target p n 1 m pion t

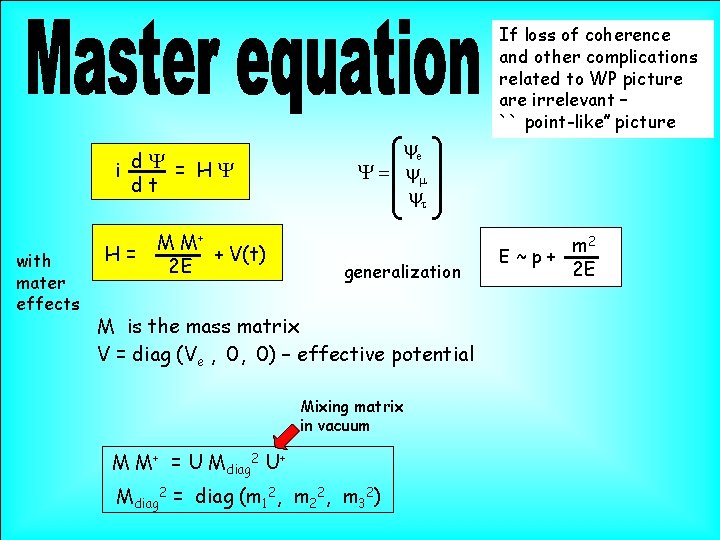
If loss of coherence and other complications related to WP picture are irrelevant – `` point-like’’ picture i d. Y = HY dt with mater effects H= M M+ + V(t) 2 E ye Y = ym yt generalization M is the mass matrix V = diag (Ve , 0, 0) – effective potential Mixing matrix in vacuum M M+ = U Mdiag 2 U+ Mdiag 2 = diag (m 12, m 22, m 32) m 2 E~p+ 2 E

y= Polarization vector: ne nt , P = y+ s/2 y P= Re ne+ nt, Im ne+ nt, ne+ ne - 1/2 Evolution equation: d. Y i = HY dt d. Y i d t = (B s ) Y B= 2 p (sin 2 qm, 0, cos 2 qm) lm Differentiating P and using equation of motion d. P = ( B x P) dt Coincides with equation for the electron spin precession in the magnetic field

n =P = (Re ne+ nt, Im ne+ nt, ne+ ne - 1/2) B= ne 2 p (sin 2 qm, 0, cos 2 qm) lm nt, Evolution equation dn = ( B x n) dt f = 2 pt/ lm - phase of oscillations P = ne+ne = n. Z + 1/2 = cos 2 q. Z/2 probability to find ne

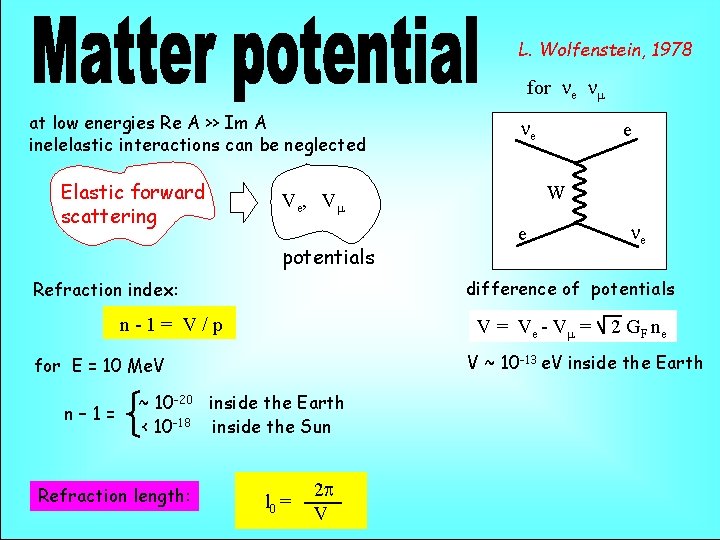
L. Wolfenstein, 1978 for ne nm at low energies Re A >> Im A inelelastic interactions can be neglected Elastic forward scattering e ne difference of potentials Refraction index: n-1= V/p V = Ve - Vm = 2 GF ne V ~ 10 -13 e. V inside the Earth for E = 10 Me. V ~ 10 -20 inside the Earth < 10 -18 inside the Sun Refraction length: e W Ve , Vm potentials n– 1= ne l 0 = 2 p V

derivation At low energies: neglect the inelastic scattering and absorption effect is reduced to the elastic forward scattering (refraction) described by the potential V: Hint(n) = < y | Hint | y > = V n n y is the wave function of the medium ne CC interactions with electrons Hint = GF n gm(1 - g ) n e g (1 - g ) e 5 m 5 2 < e g 0 (1 - g 5 ) e> = ne W e - the electron number density < e g e> = ne v < e g g 5 e > = n e l e e - averaged polarization vector of e ne For unpolarized medium at rest: V = 2 GFne

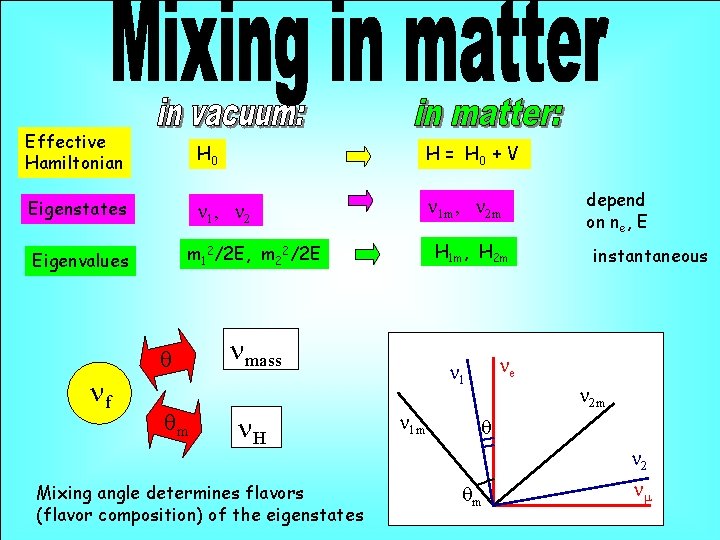
Effective Hamiltonian H 0 H = H 0 + V Eigenstates n 1, n 2 n 1 m, n 2 m q nf H 1 m, H 2 m m 12/2 E, m 22/2 E Eigenvalues qm nmass n. H Mixing angle determines flavors (flavor composition) of the eigenstates instantaneous ne n 1 m depend on ne, E n 2 m q n 2 qm nm

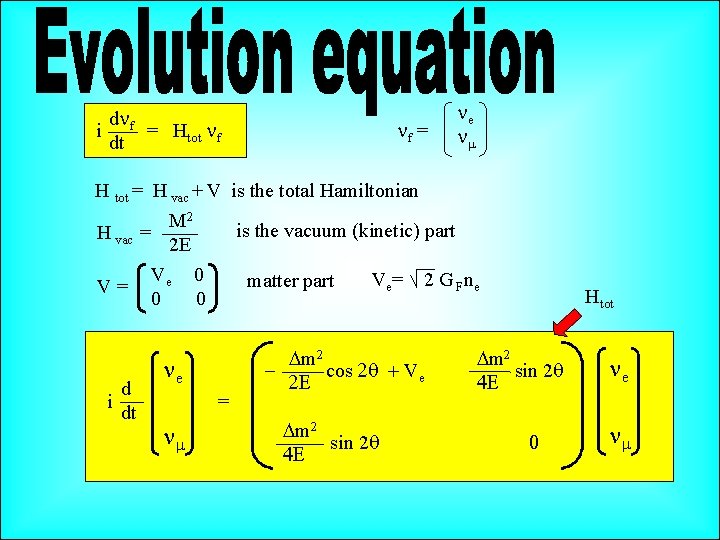
dn i f = Htot nf dt nf = ne nm H tot = H vac + V is the total Hamiltonian M 2 is the vacuum (kinetic) part H vac = 2 E V= d i dt Ve 0 0 0 matter part ne = nm Ve = 2 G Fne Dm 2 cos 2 q + Ve 2 E Dm 2 sin 2 q 4 E Htot Dm 2 sin 2 q 4 E 0 ne nm

Diagonalization of the Hamiltonian: sin 22 q m= sin 22 q V = 2 G F ne ( cos 2 q - 2 EV/Dm 2)2 + sin 22 q Mixing is maximal if V = Dm 2 cos 2 q 2 E Resonance condition sin 22 qm = 1 Difference of the eigenvalues Dm 2 ( cos 2 q - 2 EV/Dm 2)2 + sin 22 q H 2 m - H 1 m = 2 E He = H m

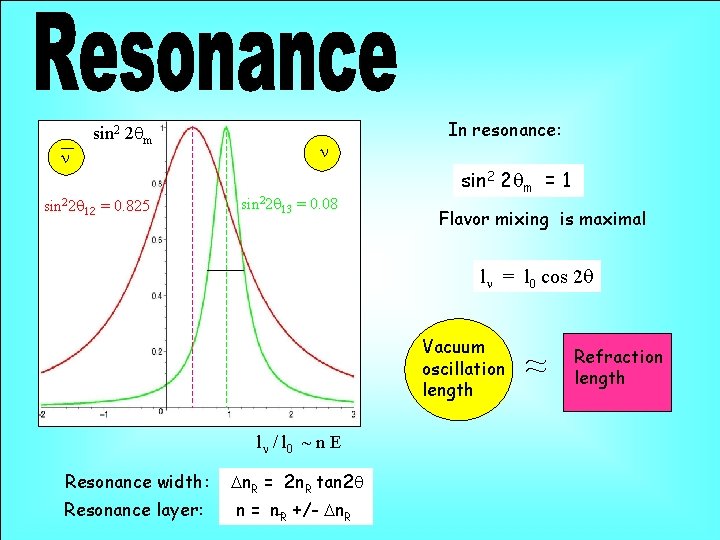
n sin 2 2 qm sin 22 q 12 = 0. 825 n sin 22 q 13 = 0. 08 In resonance: sin 2 2 qm = 1 Flavor mixing is maximal ln = l 0 cos 2 q Vacuum oscillation length ln / l 0 ~ n E Resonance width: Dn. R = 2 n. R tan 2 q Resonance layer: n = n. R +/- Dn. R ~ ~ Refraction length

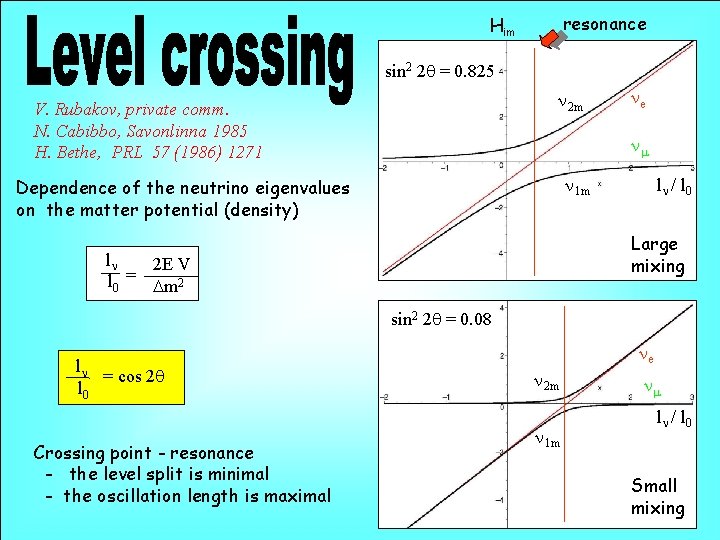
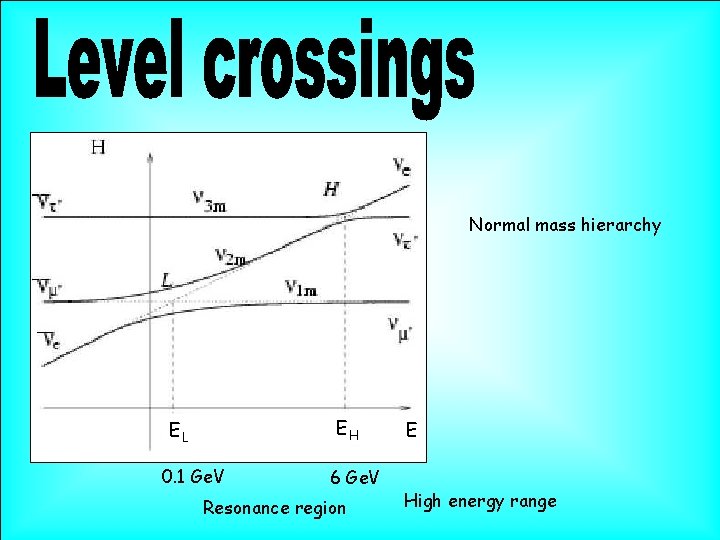
resonance Him sin 2 2 q = 0. 825 n 2 m V. Rubakov, private comm. N. Cabibbo, Savonlinna 1985 H. Bethe, PRL 57 (1986) 1271 ne nm n 1 m Dependence of the neutrino eigenvalues on the matter potential (density) ln / l 0 Large mixing ln 2 E V = l 0 Dm 2 sin 2 2 q = 0. 08 ln = cos 2 q l 0 Crossing point - resonance - the level split is minimal - the oscillation length is maximal ne n 2 m n 1 m nm ln / l 0 Small mixing

Normal mass hierarchy EH EL 0. 1 Ge. V 6 Ge. V Resonance region E High energy range

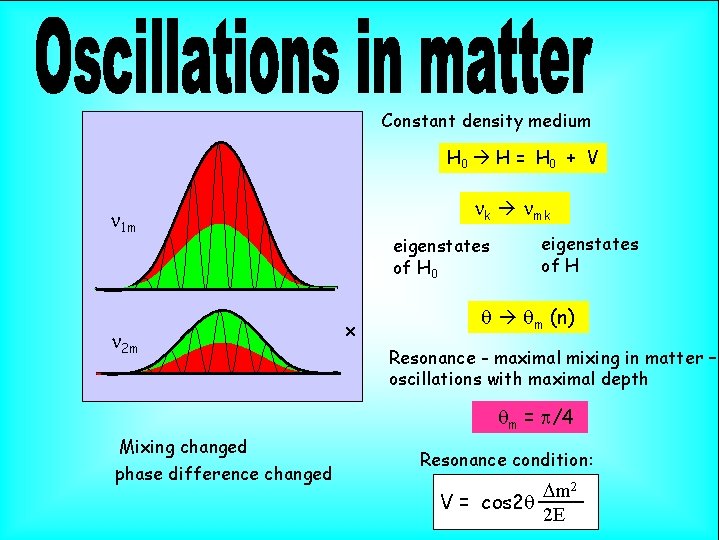
Constant density medium H 0 H = H 0 + V nk nmk n 1 m n 2 m eigenstates of H 0 x eigenstates of H q qm (n) Resonance - maximal mixing in matter – oscillations with maximal depth qm = p/4 Mixing changed phase difference changed Resonance condition: Dm 2 V = cos 2 q 2 E

Oscillation probability constant density P(ne -> na) = sin 22 qm sin 2 Amplitude of oscillations qm(E, n ) - mixing angle in matter lm(E, n ) – oscillation length in matter lm = 2 p/(H 2 m – H 1 m) Maximal effect: sin 22 qm = 1 f = p/2 + pk p. L lm half-phase f oscillatory factor In vacuum: qm q lm ln MSW resonance condition

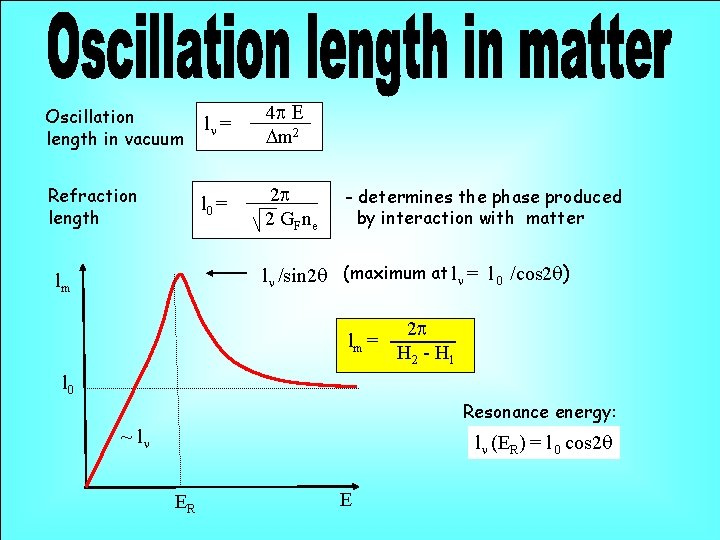
Oscillation length in vacuum ln = 4 p E Dm 2 Refraction length l 0 = 2 p 2 GFne - determines the phase produced by interaction with matter ln /sin 2 q (maximum at ln = l 0 /cos 2 q) lm lm = 2 p H 2 - H 1 l 0 Resonance energy: ~ ln ln (ER) = l 0 cos 2 q ER E

Constant density

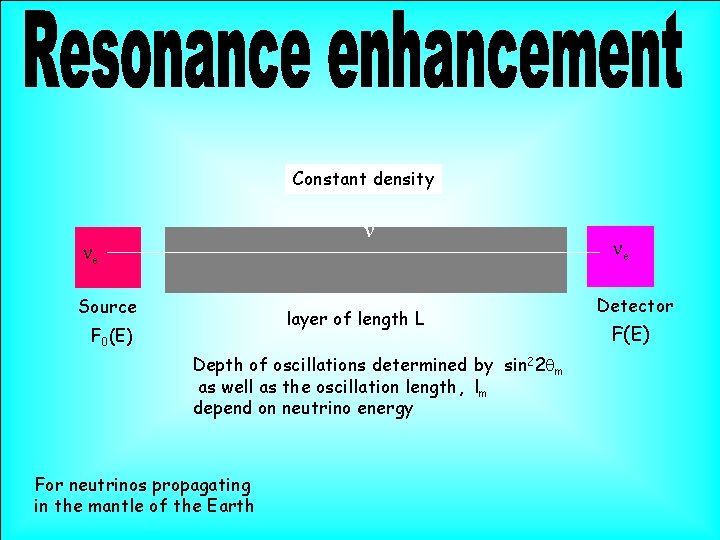
Constant density n ne Source layer of length L F 0(E) Depth of oscillations determined by sin 22 qm as well as the oscillation length, lm depend on neutrino energy For neutrinos propagating in the mantle of the Earth ne Detector F(E)

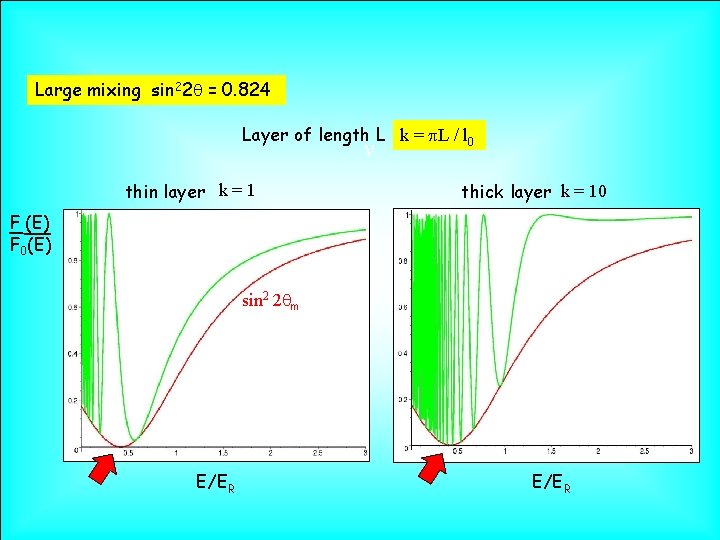
Large mixing sin 22 q = 0. 824 Layer of length L k = p. L / l 0 n thin layer k = 1 thick layer k = 10 F (E) F 0(E) sin 2 2 qm E/ER

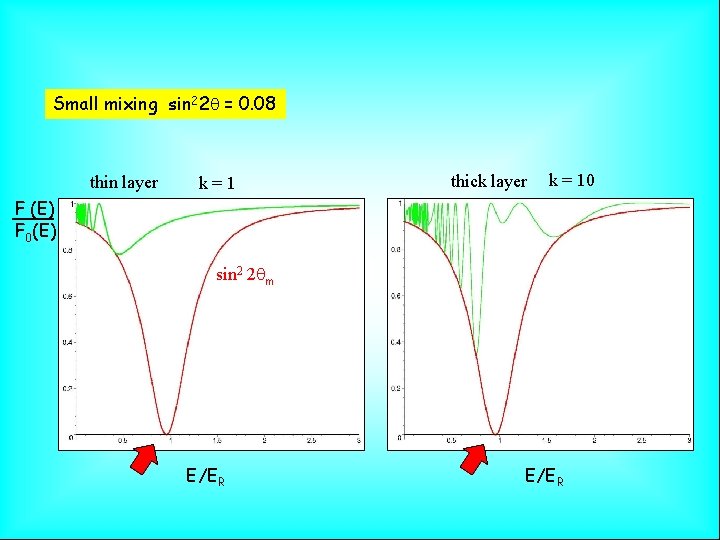
Small mixing sin 22 q = 0. 08 thin layer k=1 thick layer k = 10 F (E) F 0(E) sin 2 2 qm E/ER

Varying density

In non-uniform medium the Hamiltonian depends on time: = H tot(ne(t)) n 1 m nm = n 2 m Inserting nf = U(qm) nm n 1 m = n 2 m tot ne nf = n m dn i dt f = Htot nf d i dt H 0 dqm -i dt dqm i dt H 2 m - H 1 m qm = qm(n e(t)) n 1 m n 2 m off=diagonal terms imply transitios n 1 m n 2 m r ve owe H if dqm << H 2 m - H 1 m dt off-diagonal elements can be neglected no transitions between eigenstates propagate independently

dqm dt Adiabaticity condition transitions between the neutrino eigenstates can be neglected External conditions (density) change slowly the system has time to adjust them << H 2 m - H 1 m The eigenstates propagate independently n 1 m n 2 m Shape factors of the eigenstates do not change Crucial in the resonance layer: - the mixing changes fast - level splitting is minimal Dr. R > l. R = ln / sin 2 q if vacuum mixing is small oscillation length in resonance Dr. R = n. R / (dn/dx)R tan 2 q If vacuum mixing is large, the point of maximal adiabaticity violation is shifted to larger densities width of the res. layer n(a. v. ) -> n. R 0 = Dm 2/ 2 2 GF E

k= H 2 m - H 1 m dqm dt most crucial in the resonance where the mixing angle in matter changes fast Adiabaticity condition: k>1 k. R = Dr. R = hn tan 2 q is the width of the resonance layer n hn = is the scale of density change dn/dx l. R = ln/sin 2 q is the oscillation length in resonance Explicitly: Dm 2 sin 22 q hn k. R = 2 E cos 2 q Dr. R l. R

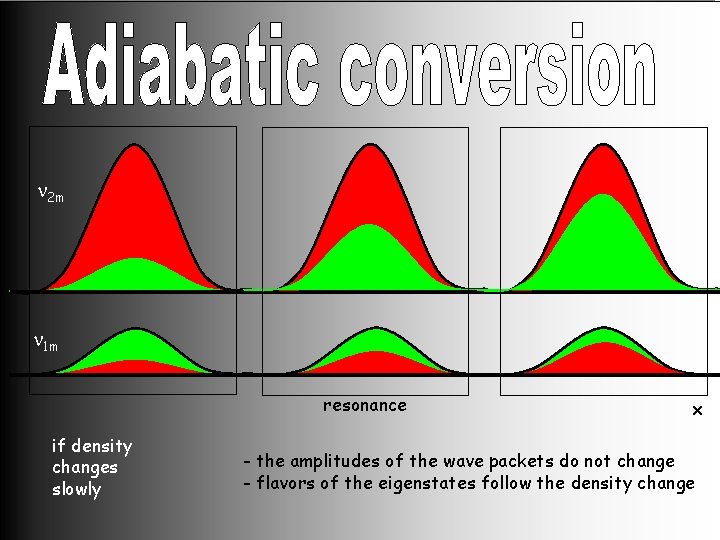
n 2 m n 1 m resonance if density changes slowly x - the amplitudes of the wave packets do not change - flavors of the eigenstates follow the density change

Sun, Supernova Initial state: From high to low densities n(0) = ne = cosqm 0 n 1 m(0) + sinqm 0 n 2 m(0) Adiabatic evolution to the surface of the Sun (zero density): Final state: Mixing angle in matter in initial state n 1 m(0) n 1 n 2 m(0) n 2 -if n(f) = cosqm 0 n 1 + sinqm 0 n 2 e Probability to find ne P = |< n | n(f) >|2 = (cosq 0)2 + (sinq 0)2 e m m averaged over oscillations = 0. 5[ 1 + cos 2 qm 0 cos 2 q ] P = sin 2 q + cos 2 qm 0

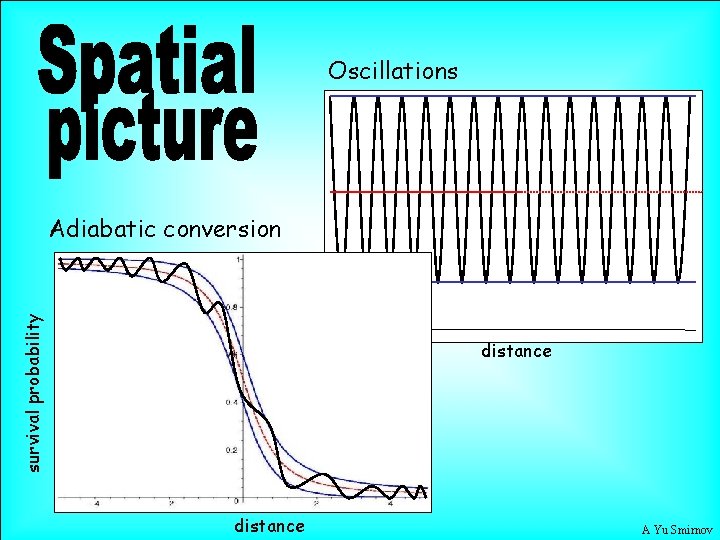
Oscillations survival probability Adiabatic conversion distance A Yu Smirnov

If density ne(t) changes fast k ~1 SN shock waves dqm dt ~ | H 2 m - H 1 m | the off-diagonal terms in the Hamiltonian can not be neglected transitions n 1 m n 2 m Admixtures of n 1 m n 2 m in a given neutrino state change ``Jump probability’’ penetration under barrier: H P 12= e H 2 m En ~ 1/hn DH H 1 m P 12= e n DH En is the energy associated to change of parameter (density) -pk. R/2 Landau-Zener

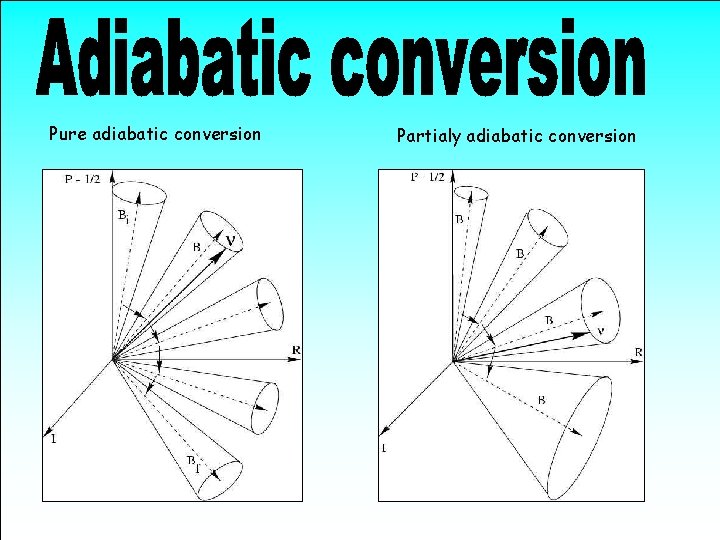
Pure adiabatic conversion ne nm Partialy adiabatic conversion

Different degrees of freedom Vacuum or uniform medium with constant parameters Non-uniform medium or/and medium with varying in time parameters Phase difference increase between the eigenstates Change of mixing in medium = change of flavor of the eigenstates qm f In non-uniform medium: interplay of both processes

ect ff MSW-e Oscillati ons Can be resonantly enhanced in matter

d. Y =HY dx M M+ H= + V(x) + … 2 E i ye Y = ym yt M is the mass matrix V = diag (Ve , 0, 0) – effective potential due to scattering on electrons M M+ = U Mdiag 2 U+ mixing matrix in vacuum Mdiag 2 = diag (m 12, m 22, m 32) ation m i x o r p ic ap Adiabat ory e h t n o i t perturba Small/large d ensity limits Approximate decoupling of some states

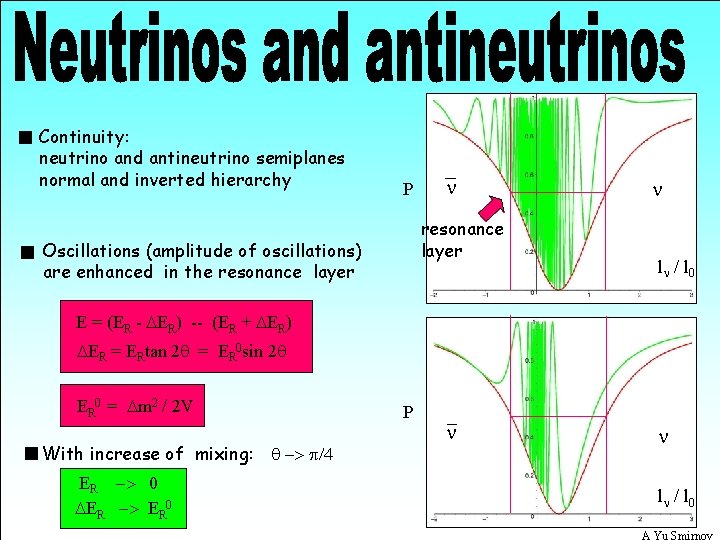
Continuity: neutrino and antineutrino semiplanes normal and inverted hierarchy P n resonance layer Oscillations (amplitude of oscillations) are enhanced in the resonance layer n ln / l 0 E = (ER - DER) -- (ER + DER) DER = ERtan 2 q = ER 0 sin 2 q ER 0 = Dm 2 / 2 V With increase of mixing: q -> p/4 ER -> 0 DER -> ER 0 P n n ln / l 0 A Yu Smirnov

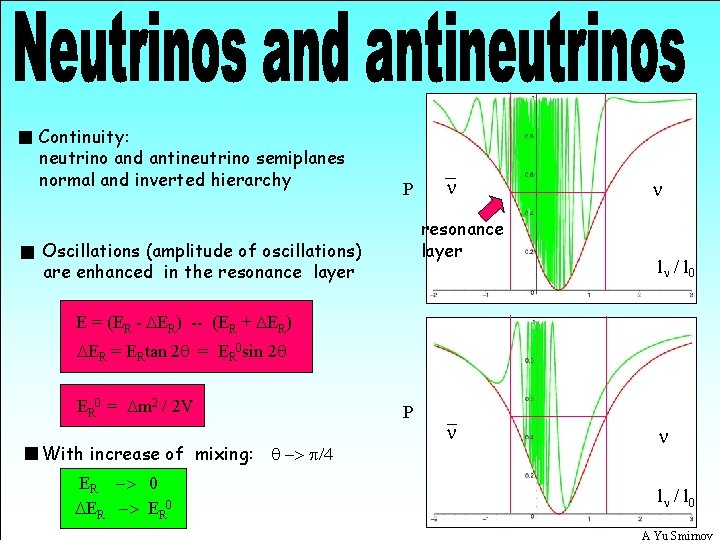
Continuity: neutrino and antineutrino semiplanes normal and inverted hierarchy P n resonance layer Oscillations (amplitude of oscillations) are enhanced in the resonance layer n ln / l 0 E = (ER - DER) -- (ER + DER) DER = ERtan 2 q = ER 0 sin 2 q ER 0 = Dm 2 / 2 V With increase of mixing: q -> p/4 ER -> 0 DER -> ER 0 P n n ln / l 0 A Yu Smirnov

`Physics derivation’ Input neutrinos are ultrarelativistic E ~ p + m 2/2 E no spin-flip, no change of the spinor structure lowest order in m/E In vacuum the mass states are the eigenstates of Hamiltonian dnmass i = dt 1 m 1 2 0 p. I + n 2 E 0 m 22 mass nmass = Using relation nmass = U+n f find equation for the flavor states: where ne nm dnf M 2 i = n dt 2 E f nf = 2 0 m 1 + M 2 = U 0 m 22 U mass matrix in flavor basis n 1 n 2 the term p. I proportional to unit matrix is omitted

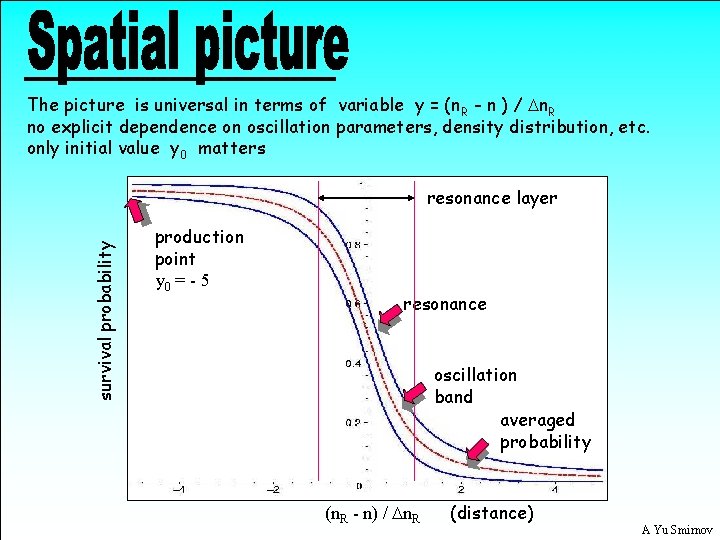
The picture is universal in terms of variable y = (n R - n ) / Dn. R no explicit dependence on oscillation parameters, density distribution, etc. only initial value y 0 matters survival probability resonance layer production point y 0 = - 5 resonance oscillation band averaged probability (n. R - n) / Dn. R (distance) A Yu Smirnov

Arbitrary state: -if(t) n (t) = cosqa n 1 m + sinqa n 2 m e Effects associated to different degrees of freedom Ø qa = qa(t) - determines the admixtures of the eigenstates Ø f (t) is the phase difference between the two eigenstates f (t) = t 0 H dt` Ø Flavors (flavor composition) of the eigenstates are determined by the mixing angle in matter <ne |n 1 m> = cosqm Ø Combination of effects Adiabaticity violation Oscillations Adiabatic conversion <nm |n 1 m> = - sin qm qa(t) + f (t) -> parametric effects, etc. qm(t) + f (t) -> ad. conv. + oscillations

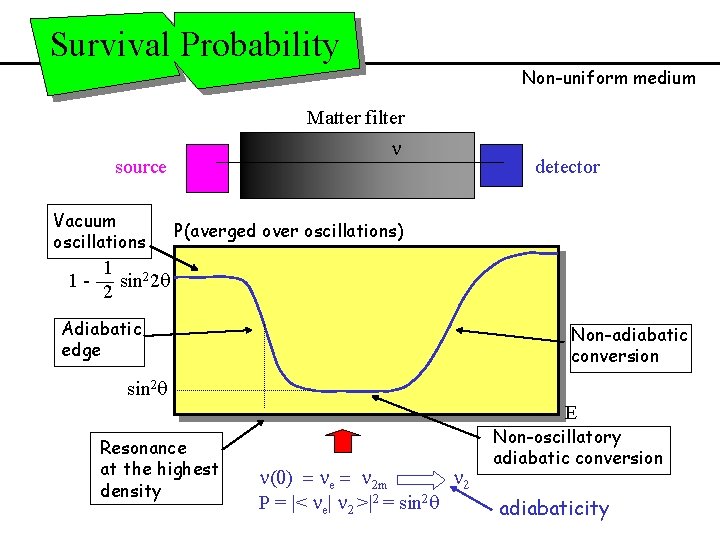
Survival Probability Non-uniform medium Matter filter n source Vacuum oscillations 1 - detector P(averged over oscillations) 1 sin 22 q 2 Adiabatic edge Non-adiabatic conversion sin 2 q E Resonance at the highest density n(0) = ne = n 2 m n 2 P = |< ne| n 2 >|2 = sin 2 q Non-oscillatory adiabatic conversion adiabaticity