A reexamination of the Mac ArthurMay theory of

A reexamination of the Mac. Arthur-May theory of species packing Olof Leimar Stockholm University • Historical background to species packing • The Mac. Arthur-May theory • Mac. Arthur's minimization principle • The importance of waste in competition • Reexamination using Fourier analysis • Is a continuum of types possible?

Some history • Why are organisms apportioned into clusters separated by gaps? (Coyne and Orr 2005) – "The manifest tendency of life toward formation of discrete arrays is not deducible from any a priori considerations. It is simply a fact to be reckoned with. " (Dobzhansky 1935) – "Homage to Santa Rosalia or Why are there so many kinds of animals? " (Hutchinson 1959) Hutchinson noted a ratio of 1: 1. 28 in size of resource extracting body parts in mammals and birds that occupied “neighboring niches” • What are the limits to similarity in coexistence?

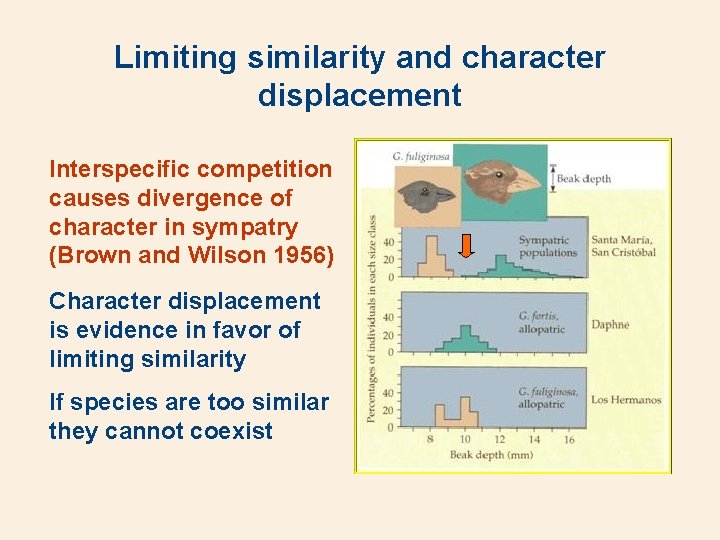
Limiting similarity and character displacement Interspecific competition causes divergence of character in sympatry (Brown and Wilson 1956) Character displacement is evidence in favor of limiting similarity If species are too similar they cannot coexist

Darwin’s finches

Mac. Arthur-May theory of species packing Robert H Mac. Arthur Robert M May Geographical ecology, 1972 Stability and complexity in model ecosystems, 1973

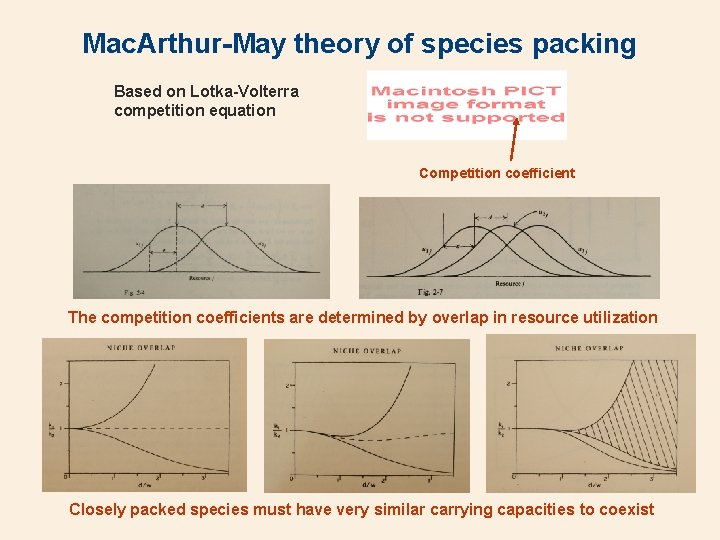
Mac. Arthur-May theory of species packing Based on Lotka-Volterra competition equation Competition coefficient The competition coefficients are determined by overlap in resource utilization Closely packed species must have very similar carrying capacities to coexist

May-Mac. Arthur community matrix analysis They assumed a large number m of equidistant species, each with the same carrying capacity and density, and with competition given by the overlap of Gaussian utilization kernels Linearization around the equilibrium gives a community matrix proportional to minus the competition matrix ij. The ij matrix is symmetric and positive definite and thus has positive eigenvalues May and Mac. Arthur (1972) approximated the smallest eigenvalue as For large overlap (small d/w) this eigenvalue is very close to zero. They referred to this near-neutrality of the community stability as “an essential singularity” They concluded that the inter-species gaps d need to be a bit larger than w for robust coexistence (e. g. in the face of environmental fluctuations)

May-Mac. Arthur community matrix analysis Lotka-Volterra dynamics: Linearization around equilibrium community: Nj = N* + Uj The equilibrium community is stable if the eigenvalues of the community matrix are negative

May-Mac. Arthur community matrix analysis May and Mac. Arthur studied matrices like These are symmetric and positive definite: For large matrices, May and Mac. Arthur claimed that the smallest eigenvalue was • They also claimed that this was approximated (for small d/w) by • The checked this numerically for different matrices A • • A circular niche-space • •

Examples (Lack, Mac. Arthur) North American tits and their European counterparts Foraging height in antbirds (Formicariidae)

Mac. Arthur’s minimization principle • Mac. Arthur (1969) “Species packing, and what interspecies competition minimizes” • Mac. Arthur (1970) “Species packing and competitive equilibrium for many species” “It has always been interesting to some scientists to construct minimum principles for their science. … Here I attempt an ecological minimum principle” The principle is, roughly, to obtain the best fit of total resource utilization to available production Lotka-Volterra competition equations Q should be minimized by the dynamics The principle only works when the competition coefficients form a symmetric matrix. The principle is nicest when this matrix is positive definite (with a close connection to a positive Fourier transform of the competition kernel), in which case there is a single local minimum (related to close-packing)

There are, of course, many different species number explanations Suggestions mentioned by Mac. Arthur (1972) There are more species where • • • there are more opportunities for speciation there are fewer hazards and catastrophes more competitors can be packed closely climate is benign climate is more stable the environment is more complex (more readily subdivided) the environment is more productive there is heavy predation (giving low abundance of each species) predators ‘sweep an area clean’ (leaving it ripe for colonization) “Some of these are almost meaningless, but most are plausible”

Reexamination of the Mac. Arthur-May theory of species packing Collaborators: Ulf Dieckmann, Michael Doebeli, Géza Meszéna, Akira Sasaki Situation to be studied Types of organisms (species) characterized by a one-dimensional trait x Nj is the population density of the type with trait xj Lotka-Volterra dynamics with and Questions to investigate: How does the shape of the competition kernel a(x) affect • the (population dynamical) stability of an equilibrium community • the uninvadability of an equilibrium community

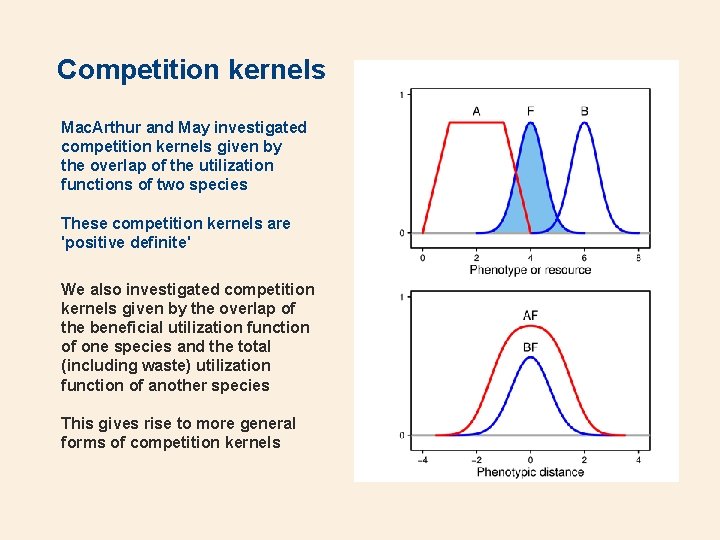
Competition kernels Mac. Arthur and May investigated competition kernels given by the overlap of the utilization functions of two species These competition kernels are 'positive definite' We also investigated competition kernels given by the overlap of the beneficial utilization function of one species and the total (including waste) utilization function of another species This gives rise to more general forms of competition kernels

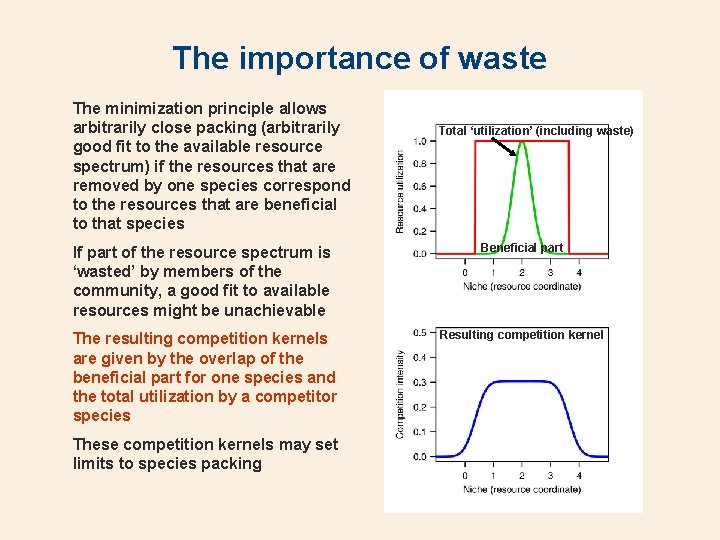
The importance of waste The minimization principle allows arbitrarily close packing (arbitrarily good fit to the available resource spectrum) if the resources that are removed by one species correspond to the resources that are beneficial to that species Total ‘utilization’ (including waste) If part of the resource spectrum is ‘wasted’ by members of the community, a good fit to available resources might be unachievable Beneficial part The resulting competition kernels are given by the overlap of the beneficial part for one species and the total utilization by a competitor species Resulting competition kernel These competition kernels may set limits to species packing

Examples of waste in competition • Birds ‘dropping seeds’ that are too small or too large to be optimal for their beak; the dropped seeds are eaten by mice rather than by competitors • Predators scaring prey (or inducing defenses in prey) that are outside of their hunting range • Different forms of ‘excessive’ territoriality • Mammal herbivores trampling plants that might be suitable for competitors So-called trait-mediated interactions between predators and prey have been studied a lot in recent years

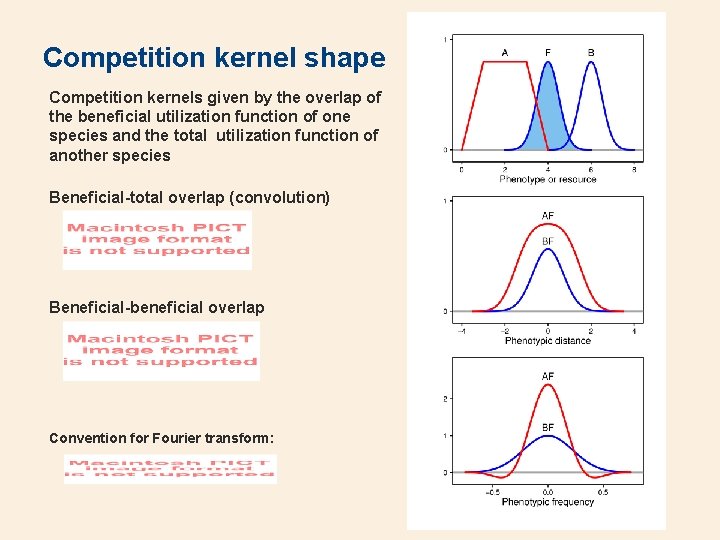
Competition kernel shape Competition kernels given by the overlap of the beneficial utilization function of one species and the total utilization function of another species Beneficial-total overlap (convolution) Beneficial-beneficial overlap Convention for Fourier transform:

Three limiting similarity results • First result on species packing A version of our problem The stability of an equilibrium community given by the distribution n(x) (the previous formulation corresponds to with ) Assumptions about the competition kernel Equilibrium community (infinitely close-packed) Fourier transform of (generalized) function f(x) Result 1 The equilibrium community n(x) = is stable if the Fourier transform â( ) of the competition kernel a(x) is positive and unstable if â( ) changes sign

Verification of Result 1 The equation is Linearization around equilibrium community; n(x) = + u(x) Fourier transform of the linearized equation (our assumptions about a(x) imply that â( ) is real and symmetric and that â(0) > 0) We see that all small perturbations (i. e. with any frequency ) of the equilibrium die down if â( ) > 0. If â( ) < 0 for some frequency , the corresponding perturbation will grow, destabilizing the equilibrium.

Some Fourier analysis we need Poisson’s summation formula where a(x) is a continuous function of bounded variation with The following two relations are versions of Poisson’s summation formula is since the transform of and the transform of is

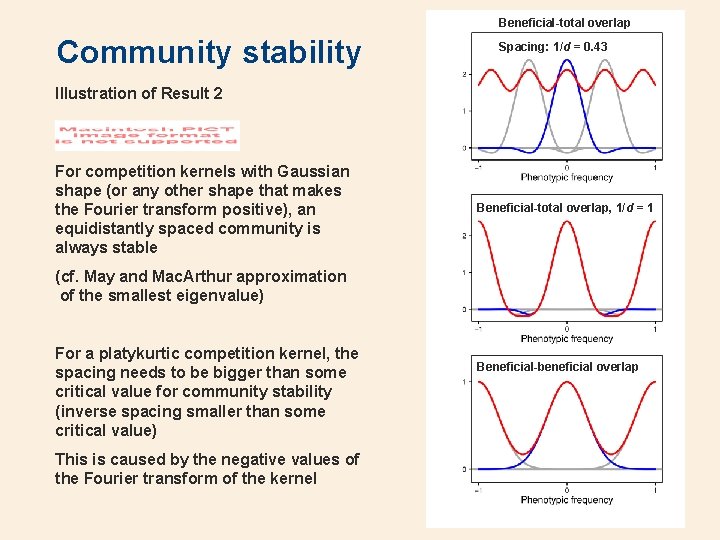
• Second result on species packing Community stability for�equidistantly spaced community on the real line • with • By requiring periodicity with period md, i. e. Nj+m = Nj, we get a community on a “circular trait-space” • The “sampled” kernel has the Fourier transform The equilibrium community Nj = N* is stable if the Fourier transform ( ) of the “sampled” kernel A(x) is positive and unstable if ( ) changes sign Note that ( ) is periodic with period 1/d, so ( ) for 0 < 1/d is enough For a community on a circle, only frequencies = k/(md) with 0 k < m apply Note that ( ) approaches â( ) as d goes to zero and that > 0 holds if â > 0 • A circular niche-space Equilibrium community: Result 2 • •

Verification of Result 2 The equation is Linearization around equilibrium community; Nj = N* + Uj Writing the deviation as where the linearized equation becomes ; the Fourier transform of the linearized equation is then

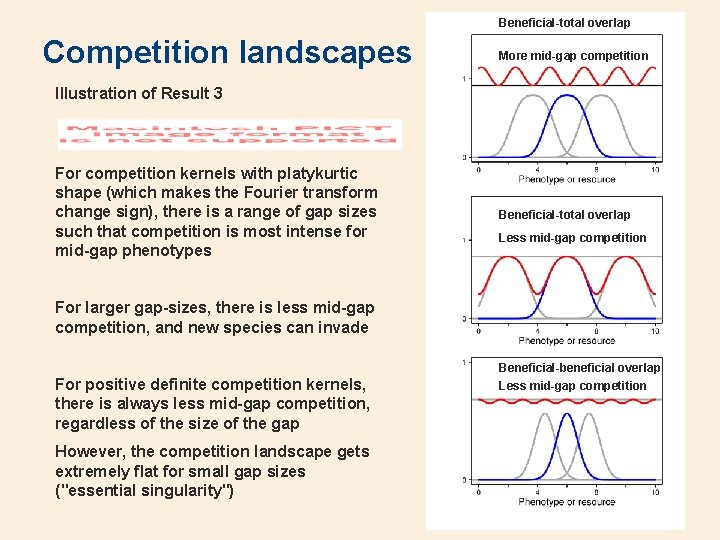
• Third result on species packing Uninvadability for�equidistantly spaced equilibrium community on the real line with to first order Fitness landscape From Poisson’s summation formula Since F(0) = 0, we have Result 3 (i) The equilibrium community Nj = N* is uninvadable if F(x) is non-positive (ii) If the competition kernel a(x) has a positive Fourier transform â( ), every equidistantly spaced community is invadable If â(1/d) is substantially less than zero, there is “a good chance” that the equilibrium community with spacing d is uninvadable If â(k/d) < 0 for k > 0 the community is uninvadable

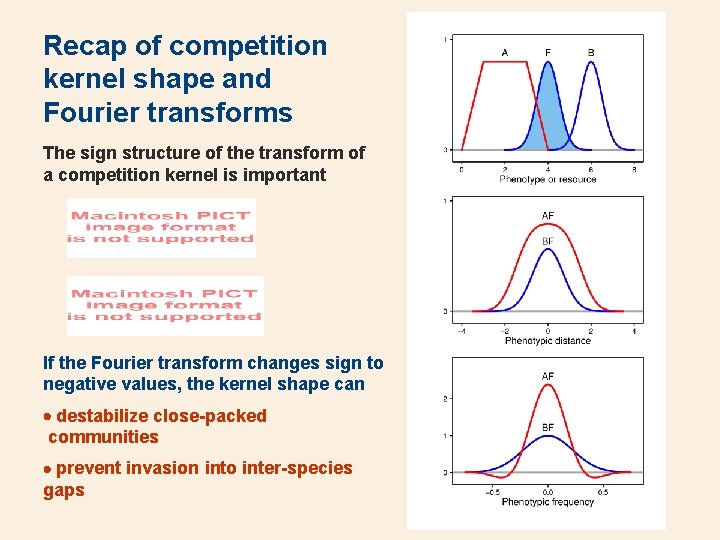
Recap of competition kernel shape and Fourier transforms The sign structure of the transform of a competition kernel is important If the Fourier transform changes sign to negative values, the kernel shape can destabilize close-packed communities prevent invasion into inter-species gaps

Beneficial-total overlap Community stability Spacing: 1/d = 0. 43 Illustration of Result 2 For competition kernels with Gaussian shape (or any other shape that makes the Fourier transform positive), an equidistantly spaced community is always stable Beneficial-total overlap, 1/d = 1 (cf. May and Mac. Arthur approximation of the smallest eigenvalue) For a platykurtic competition kernel, the spacing needs to be bigger than some critical value for community stability (inverse spacing smaller than some critical value) This is caused by the negative values of the Fourier transform of the kernel Beneficial-beneficial overlap

Beneficial-total overlap Competition landscapes More mid-gap competition Illustration of Result 3 For competition kernels with platykurtic shape (which makes the Fourier transform change sign), there is a range of gap sizes such that competition is most intense for mid-gap phenotypes Beneficial-total overlap Less mid-gap competition For larger gap-sizes, there is less mid-gap competition, and new species can invade For positive definite competition kernels, there is always less mid-gap competition, regardless of the size of the gap However, the competition landscape gets extremely flat for small gap sizes ("essential singularity") Beneficial-beneficial overlap Less mid-gap competition

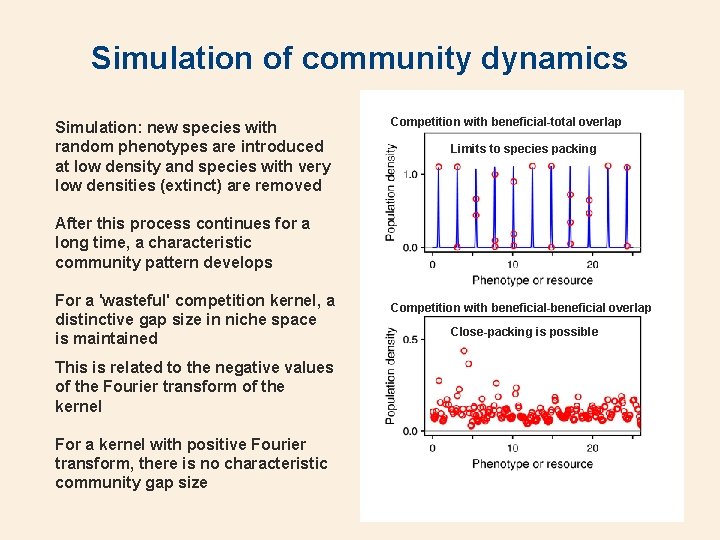
Simulation of community dynamics Simulation: new species with random phenotypes are introduced at low density and species with very low densities (extinct) are removed Competition with beneficial-total overlap Limits to species packing After this process continues for a long time, a characteristic community pattern develops For a 'wasteful' competition kernel, a distinctive gap size in niche space is maintained This is related to the negative values of the Fourier transform of the kernel For a kernel with positive Fourier transform, there is no characteristic community gap size Competition with beneficial-beneficial overlap Close-packing is possible

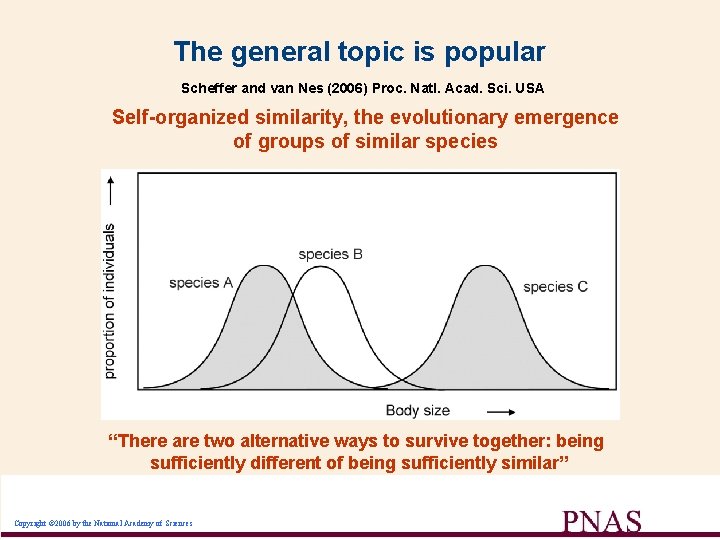
The general topic is popular Scheffer and van Nes (2006) Proc. Natl. Acad. Sci. USA Self-organized similarity, the evolutionary emergence of groups of similar species “There are two alternative ways to survive together: being sufficiently different of being sufficiently similar” Copyright © 2006 by the National Academy of Sciences

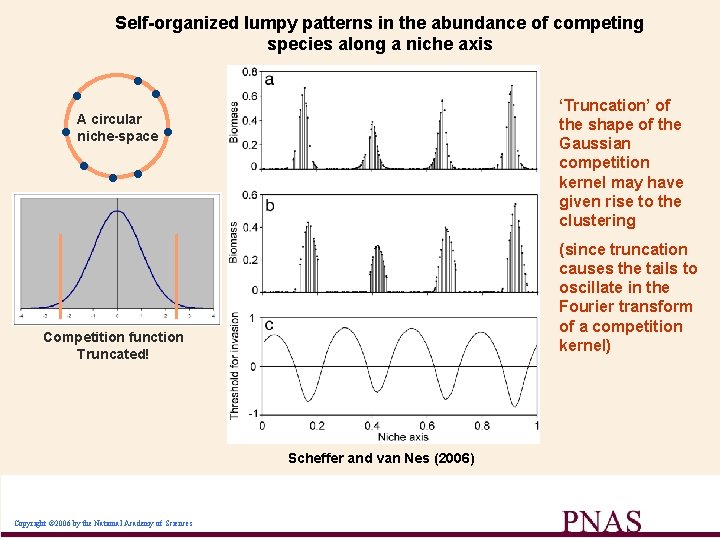
Self-organized lumpy patterns in the abundance of competing species along a niche axis • • • • A circular niche-space ‘Truncation’ of the shape of the Gaussian competition kernel may have given rise to the clustering • • (since truncation causes the tails to oscillate in the Fourier transform of a competition kernel) Competition function Truncated! Scheffer and van Nes (2006) Copyright © 2006 by the National Academy of Sciences

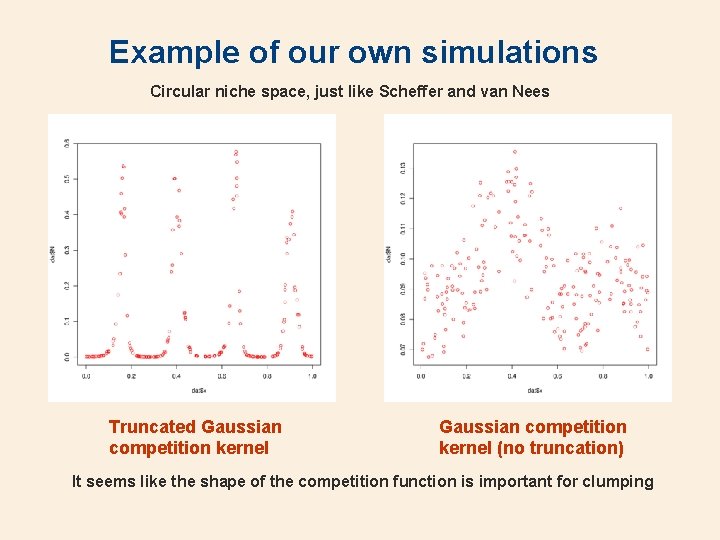
Example of our own simulations Circular niche space, just like Scheffer and van Nees Truncated Gaussian competition kernel (no truncation) It seems like the shape of the competition function is important for clumping

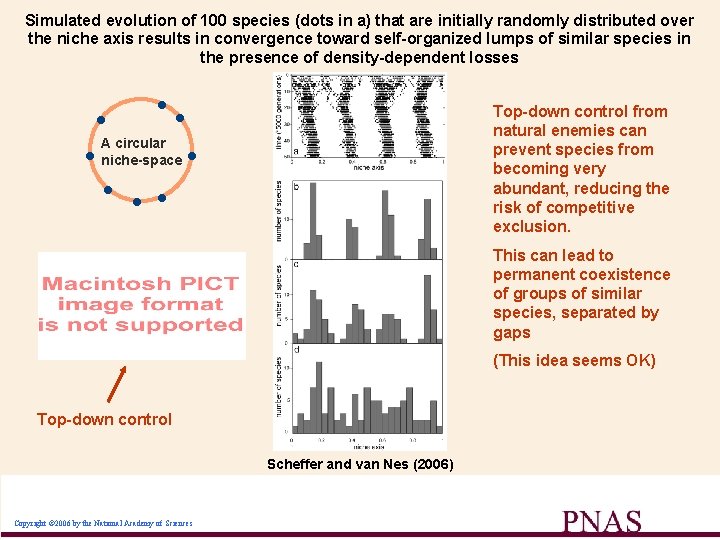
Simulated evolution of 100 species (dots in a) that are initially randomly distributed over the niche axis results in convergence toward self-organized lumps of similar species in the presence of density-dependent losses • • • • A circular niche-space Top-down control from natural enemies can prevent species from becoming very abundant, reducing the risk of competitive exclusion. • • This can lead to permanent coexistence of groups of similar species, separated by gaps (This idea seems OK) Top-down control Scheffer and van Nes (2006) Copyright © 2006 by the National Academy of Sciences

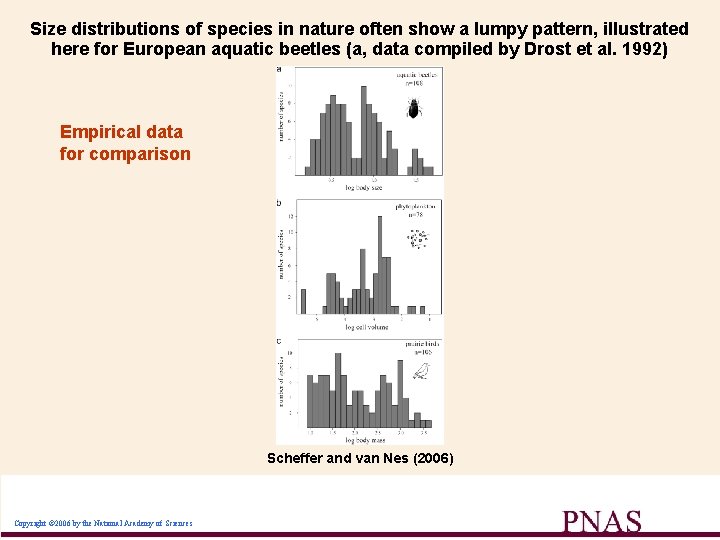
Size distributions of species in nature often show a lumpy pattern, illustrated here for European aquatic beetles (a, data compiled by Drost et al. 1992) Empirical data for comparison Scheffer and van Nes (2006) Copyright © 2006 by the National Academy of Sciences

Summing up • The shape of competition kernels influences species packing and limiting similarity • Shapes such that the Fourier transform of the kernel changes sign destabilize very close packing • These shapes can also, for situations with intermediate interspecies gaps, prevent invasion into the gaps • There can be rather strong selection against invasion into the gap • Waste in resource utilization is one possible cause of such competition kernel shapes