18 337 Parallel Prefix 18 337 The Parallel

18. 337 Parallel Prefix 18. 337

The Parallel Prefix Method – This is our first example of a parallel algorithm – Watch closely what is being optimized for • Parallel steps – Beautiful idea with surprising uses – Not sure if the parallel prefix method is used much in the real world • Might maybe be inside MPI scan • Might be used in some SIMD and SIMD like cases – The real key: What is it about the real world that differs from the naïve mental model of parallelism? 18. 337

Students early mental models • Look up or figure out how to do things in parallel • Then we get speedups! – NOT! 18. 337

Parallel Prefix Algorithms 1. A theoretical (may or may not be practical) secret to turning serial into parallel 2. Suppose you bump into a parallel algorithm that surprises you “there is no way to parallelize this algorithm” you say 3. Probably a variation on parallel prefix! 18. 337

Example of a prefix Sum Prefix Input x = (x 1, x 2, . . . , xn) Output y = (y 1, y 2, . . . , yn) yi = Σj=1: I xj Example x = ( 1, 2, 3, 4, 5, 6, 7, 8 ) y = ( 1, 3, 6, 10, 15, 21, 28, 36) Prefix Functions-- outputs depend upon an initial string 18. 337

What do you think? • Can we really parallelize this? • It looks like this sort of code: y=0; for i=2: n, y(i)=y(i-1)+x(i); end • The ith iteration of the loop is not at all decoupled from the (i-1)st iteration. • Impossible to parallelize right? 18. 337

A clue? x = ( 1, 2, 3, 4, 5, 6, 7, 8 ) y = ( 1, 3, 6, 10, 15, 21, 28, 36) Is there any value in adding, say, 4+5+6+7? Note if we separately have 1+2+3, what can we do? Suppose we added 1+2, 3+4, etc. pairwise, what could we do? 18. 337

Prefix Functions -- outputs depend upon an initial string Suffix Functions -- outputs depend upon a final string Other Notations 1. + “plus scan” APL (“A Programming Language” source of the very name “scan”, an array based language that was ahead of its time) 2. MPI_scan 3. MATLAB command: y=cumsum(x) 4. MATLAB matmul: y=tril(ones(n))*x 18. 337

Parallel Prefix Recursive View prefix( [1 2 3 4 5 6 7 8])=[1 3 6 10 15 21 28 36] 1 2 3 4 5 6 7 8 3 7 11 15 3 10 21 36 1 3 6 10 15 21 28 36 • Any associative operator 100 111 18. 337 Pairwise sums Recursive prefix Update “odds”

MATLAB simulation function y=prefix(x) n=length(x); if n==1, y=x; else w=x(1: 2: n)+x(2: 2: n); % Pairwise adds w=prefix(w); % Recur y(1: 2: n)= x(1: 2: n)+[0 w(1: end-1) ]; y(2: 2: n)=w; % Update Adds end What does this reveal? What does this hide? 18. 337

Operation Count • Notice • # adds = 2 n • # required = n • Parallelism at the cost of more work! 18. 337

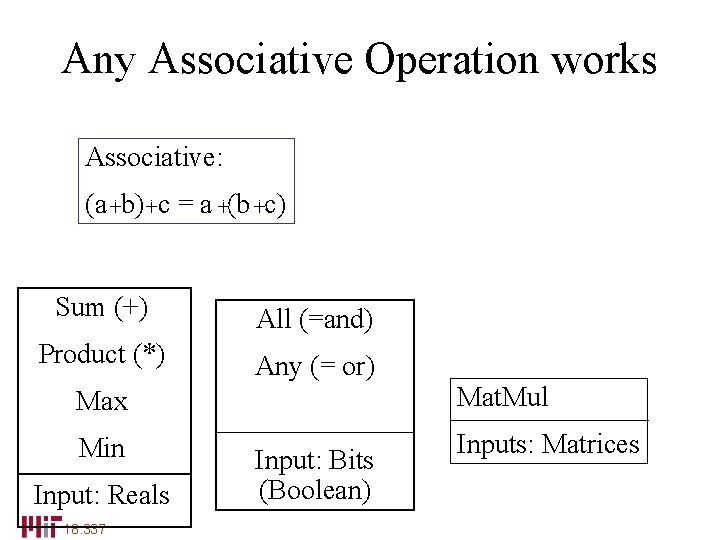
Any Associative Operation works Associative: (a +b) +c = a +(b +c) Sum (+) All (=and) Product (*) Any (= or) Max Mat. Mul Min Inputs: Matrices Input: Reals 18. 337 Input: Bits (Boolean)

Fibonacci via Matrix Multiply Prefix Fn+1 = Fn + Fn-1 Can compute all Fn by matmul_prefix on [ , , , , ] then select the upper left entry 18. 337

Arithmetic Modulo 2 (binary arithmetic) 0+0=0 0+1=1 1+0=1 1+1=0 Add = exclusive or 18. 337 0*0=0 0*1=0 1*0=0 1*1=1 Mult = and

Carry-Look Ahead Addition (Babbage 1800’s) Example 1 0 1 1 1 Carry 1 0 1 1 1 First Int 1 0 1 Second Int 1 0 1 1 0 0 Sum Goal: Add Two n-bit Integers 18. 337

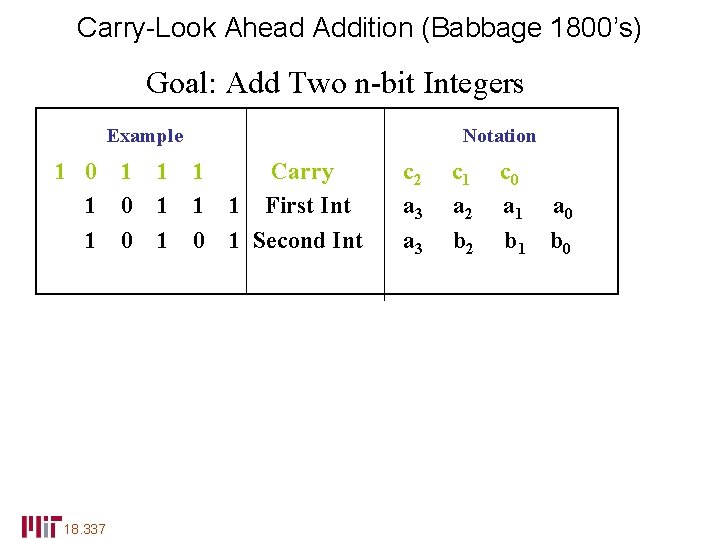
Carry-Look Ahead Addition (Babbage 1800’s) Goal: Add Two n-bit Integers Example 1 0 1 1 1 Carry 1 0 1 1 1 First Int 1 0 1 Second Int 1 0 1 1 0 0 Sum 18. 337 Notation c 2 a 3 s 3 c 1 a 2 b 2 s 2 c 0 a 1 b 1 s 1 a 0 b 0 s 0

Carry-Look Ahead Addition (Babbage 1800’s) Goal: Add Two n-bit Integers Example Notation 1 0 1 1 1 Carry c 2 c 1 c 0 1 1 1 First Int a 3 a 2 a 1 1 0 1 Second Int a 3 b 2 b 1 1 0 0 Sum s 3 s 2 s 1 c-1 = 0 (addition mod 2) for i = 0 : n-1 a 0 b 0 si = ai + bi + ci-1 ci = aibi + ci-1(ai + bi) end 18. 337 sn = cn-1

Carry-Look Ahead Addition (Babbage 1800’s) Goal: Add Two n-bit Integers Example Notation 1 0 1 1 1 Carry 1 0 1 1 1 First Int 1 0 1 Second Int 1 0 1 1 0 0 Sum c-1 = 0 (addition mod 2) for i = 0 : n-1 ci s =a +b +c i i-1 ci = aibi + ci-1(ai + bi) end sn = cn-1 18. 337 1 c 2 a 3 s 3 = c 1 a 2 b 2 s 2 c 0 a 1 b 1 s 1 a 0 b 0 s 0 ai + bi aibi ci-1 0 1 1

Carry-Look Ahead Addition (Babbage 1800’s) Goal: Add Two n-bit Integers Example Notation 1 0 1 1 1 Carry 1 0 1 1 1 First Int 1 0 1 Second Int 1 0 1 1 0 0 Sum c-1 = 0 (addition mod 2) for i = 0 : n-1 si = ai + bi + ci-1 ci = aibi + ci-1(ai + bi) end s = cn-1 18. 337 n ci c 2 a 3 s 3 c 1 a 2 b 2 s 2 ai + bi c 0 a 1 b 1 s 1 a 0 b 0 s 0 aibi ci-1 1 = 0 1 1 Matmul prefix with binary arithmetic is equivalent to carry-look ahead! Compute ci by prefix, then si = ai + bi +ci-1 in parallel

[ ] Tridiagonal Factor a 1 b 1 c 1 a 2 b 2 T Determinants (D 0=1, D 1=a 1) (Dk is the det of the kxk upper left): Dn-1 c 2 a 3 b 3 = Dn c 3 a 4 b 4 Dn = an Dn-1 - bn-1 cn-1 Dn-2 c 4 a 5 Dn = Dn-1 an -bn-1 cn-1 Dn-1 1 0 Dn-2 1 T 3 embarassing Parallels + prefix 18. 337 Compute Dn by matmul_prefix = d 1 b 1 l 1 1 l 2 1 d 2 b 2 d 3 dn = Dn/Dn-1 ln = cn/dn

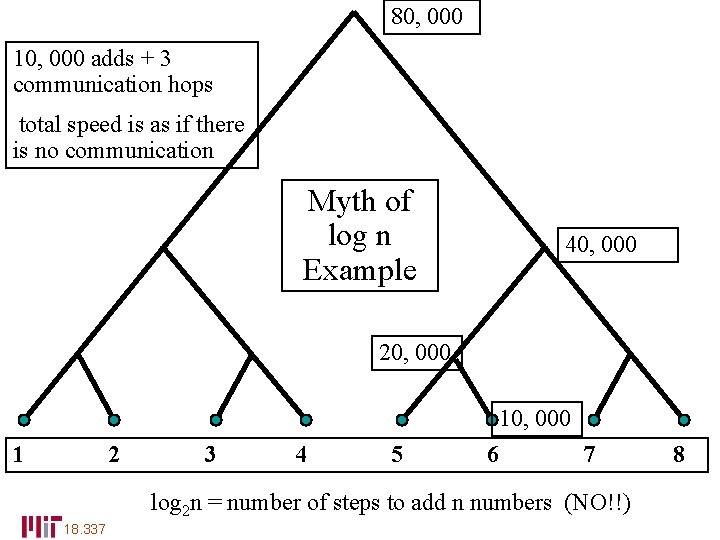
The “Myth” of log n The log 2 n parallel steps is not the main reason for the usefulness of parallel prefix. Say n = 1000 p (1000 summands per processor) Time = (2000 adds) + (log 2 P message passings) fast & embarassingly parallel (2000 local adds are serial for each 18. 337

80, 000 10, 000 adds + 3 communication hops total speed is as if there is no communication Myth of log n Example 40, 000 20, 000 1 2 3 4 5 6 7 log 2 n = number of steps to add n numbers (NO!!) 18. 337 8

Any Prefix Operation May Be Segmented! 18. 337

Segmented Operations Inputs = Ordered Pairs (operand, boolean) e. g. (x, T) or (x, F) (y, T) (y, F) (x, T) (x+ y, T) (y, F) (x, F) (y, T) (xÅy, F) +2 e. g. Result 18. 337 Change of segment indicated by switching T/F 1 2 3 4 5 6 7 8 T T F F F T 1 3 3 7 12 6 7 8

Copy Prefix: x +y = x (is associative) Segmented 1 T 1 18. 337 2 T 1 3 F 3 4 F 3 5 F 3 6 T 6 7 F 7 8 T 8

High Performance Fortran SUM_PREFIX ( ARRAY, DIM, MASK, SEG, EXC) A= 1 2 3 4 5 6 7 8 9 10 M= 11 12 13 14 15 1 20 42 67 45 7 27 50 76 105 18 39 63 90 120 SUM_SUFFIX(A) 1 3 6 10 15 SUM_PREFIX(A, DIM = 2) = 6 13 21 30 40 11 23 36 1 14 17 . 1 14 25 . 12 14 38 SUM_PREFIX(A) = SUM_PREFIX(A, MASK = M) = 18. 337 T T T F F T T F T F F

More HPF Segmented A= 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 T T |F| T T| F F S= T F T T F F T T Sum_Prefix (A, SEGMENTS = S) 1 13 3 6 20 11 32 18. 337

Example of Exclusive A= 1 2 3 4 5 Sum_Prefix(A) 1 3 6 10 15 Sum_Prefix(A, EXCLUSIVE = TRUE) 0 1 3 6 10 (Exclusive: Don’t count myself) 18. 337

Parallel Prefix prefix( [1 2 3 4 5 6 7 8])=[1 3 6 10 15 21 28 36] 1 2 3 4 5 6 7 8 3 7 11 15 3 10 21 36 Pairwise sums Recursive prefix Update “evens” 1 3 6 10 15 21 28 36 • Any associative operator • AKA: + (APL), cumsum(Matlab), MPI_SCAN, 100 111 18. 337

Variations on Prefix exclusive( [1 2 3 4 5 6 7 8])=[0 1 3 6 10 15 21 28] 1 2 3 4 5 6 7 8 3 7 11 15 0 3 10 21 0 1 3 6 10 15 21 28 18. 337 1)Pairwise Sums 2)Recursive Prefix 3)Update “odds”

Variations on Prefix exclusive( [1 2 3 4 5 6 7 8])=[0 1 3 6 10 15 21 28] 1 2 3 4 5 6 7 8 3 7 11 15 0 3 10 21 0 1 3 6 10 15 21 28 1)Pairwise Sums 2)Recursive Prefix 3)Update “odds” The Family. . . Directions Inclusive Exc=0 Exc=1 Prefix Exc Prefix Left 18. 337

Variations on Prefix exclusive( [1 2 3 4 5 6 7 8])=[0 1 3 6 10 15 21 28] 1 2 3 4 5 6 7 8 3 7 11 15 0 3 10 21 0 1 3 6 10 15 21 28 1)Pairwise Sums 2)Recursive Prefix 3)Update “evens” The Family. . . Directions Inclusive Exc=0 Prefix Left Suffix Right 18. 337 Exclusive Exc=1 Exc Prefix Exc Suffix

Variations on Prefix reduce( [1 2 3 4 5 6 7 8])=[36 36 36] 1 2 3 4 5 6 3 7 11 36 36 36 7 8 15 36 36 36 1)Pairwise Sums 2)Recursive Reduce 3)Update “odds” The Family. . . Directions Inclusive Exc=0 Prefix Left Suffix Right Left/Right Reduce 18. 337 Exclusive Exc=1 Exc Prefix Exc Suffix Exc Reduce

Variations on Prefix exclusive( [1 2 3 4 5 6 7 8])=[0 1 3 6 10 15 21 28] 1 2 3 4 5 6 7 8 3 7 11 15 0 3 10 21 0 1 3 6 10 15 21 28 1)Pairwise Sums 2)Recursive Prefix 3)Update “evens” The Family. . . Directions Inclusive Exc=0 Prefix Left Suffix Right Left/Right Reduce 18. 337 Exclusive Neighbor Exc=1 Exc=2 Exc Prefix Left Multipole Exc Suffix Right " " " Exc Reduce Multipole

Multipole in 2 d or 3 d etc Notice that left/right generalizes more readily to higher dimensions Ask yourself what Exc=2 looks like in 3 d The Family. . . Directions Inclusive Exc=0 Prefix Left Suffix Right Left/Right Reduce 18. 337 Exclusive Neighbor Exc=1 Exc=2 Exc Prefix Left Multipole Exc Suffix Right " " " Exc Reduce Multipole

Not Parallel Prefix but PRAM § Only concerned with minimizing parallel time (not communication) § Arbitrary number of processors § One element per processor 18. 337

Csanky’s (1977) Matrix Inversion Lemma 1: ( Proof Idea: -1) in O(log 2 n) (triangular matrix inv) A 0 -1 A-1 0 = C B -B-1 CA-1 B-1 Lemma 2: Cayley - Hamilton p(x) = det (x. I - A) = xn + c 1 xn-1 +. . . + cn ± (cn = det A) 0 = p(A) = An + c 1 An-1 +. . . + cn. I A-1 = (An-1 + c 1 An-2 +. . . + cn-1)(-1/cn) Powers of A via Parallel Prefix 18. 337

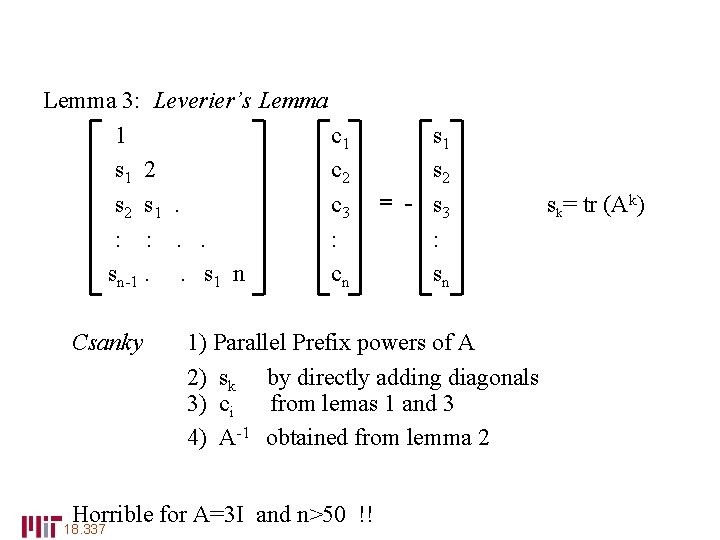
Lemma 3: Leverier’s Lemma 1 c 1 s 1 2 c 2 s 1. c 3 : : . . : sn-1. . s 1 n cn Csanky 1) Parallel Prefix powers of A 2) sk by directly adding diagonals 3) ci from lemas 1 and 3 4) A-1 obtained from lemma 2 Horrible for A=3 I and n>50 !! 18. 337 s 1 s 2 = - s 3 : sn sk= tr (Ak)

Matrix multiply can be done in log n steps on n 3 processors with the pram model Can be useful to think this way, but must also remember how real machines are built! • Parallel steps are not the whole story • Nobody puts one element per processor 18. 337