Parallel Prefix Sum Scan GPU Graphics Gary J

Parallel Prefix Sum (Scan) GPU Graphics Gary J. Katz University of Pennsylvania CIS 665 Adapted from articles taken from GPU Gems III

Scan o Definition: n The all-prefix-sums operation takes a binary associative operator with identity I, and an array of n elements [a 0, a 1, …, an-1] and returns the array [I, a 0, (a 0 a 1), … , (a 0 o a 1 … Example: [ 1 13 35 2 6 8 10 23 52 11 26 19 ] [ 0 1 14 49 51 57 65 75 98 150 161 187 206] an-2)]

Sequential Scan out[0] = 0; for (k = 1; k < n; k++) out[k] = in[k-1] + out[k -1]; o o Performs n adds for an array length of n Work Complexity is O(n)

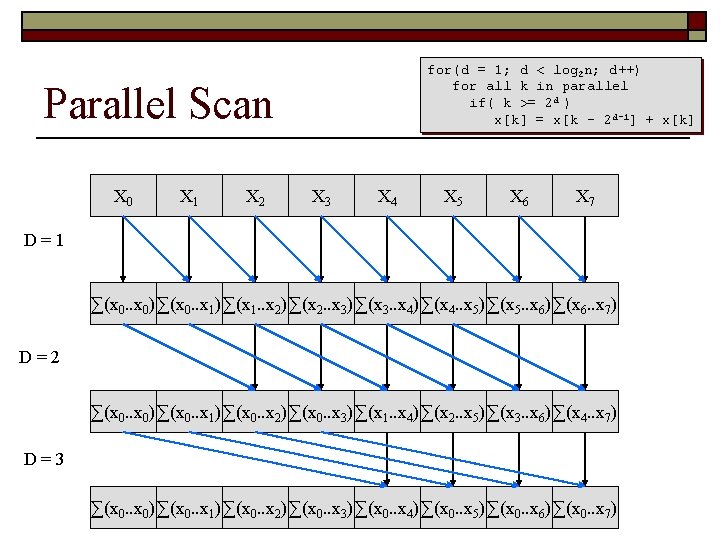
Parallel Scan for(d = 1; d < log 2 n; d++) for all k in parallel if( k >= 2 d ) x[k] = x[k – 2 d-1] + x[k] o o Performs O(nlog 2 n) addition operations Assumes there as many processors as data elements

for(d = 1; d < log 2 n; d++) for all k in parallel if( k >= 2 d ) x[k] = x[k – 2 d-1] + x[k] Parallel Scan X 0 X 1 X 2 X 3 X 4 X 5 X 6 X 7 D=1 ∑(x 0. . x 0) ∑(x 0. . x 1) ∑(x 1. . x 2) ∑(x 2. . x 3) ∑(x 3. . x 4) ∑(x 4. . x 5) ∑(x 5. . x 6) ∑(x 6. . x 7) D=2 ∑(x 0. . x 0) ∑(x 0. . x 1) ∑(x 0. . x 2) ∑(x 0. . x 3) ∑(x 1. . x 4) ∑(x 2. . x 5) ∑(x 3. . x 6) ∑(x 4. . x 7) D=3 ∑(x 0. . x 0) ∑(x 0. . x 1) ∑(x 0. . x 2) ∑(x 0. . x 3) ∑(x 0. . x 4) ∑(x 0. . x 5) ∑(x 0. . x 6) ∑(x 0. . x 7)

Parallel Scan for(d = 1; d < log 2 n; d++) for all k in parallel if( k >= 2 d ) x[k] = x[k – 2 d-1] + x[k] o What’s the problem with this algorithm for the GPU?

Parallel Scan for(d = 1; d < log 2 n; d++) for all k in parallel if( k >= 2 d ) x[out][k] = x[in][k – 2 d-1] + x[in][k] else x[out][k] = x[in][k] o GPU needs to double buffer the array

Issues with Current Implementation? o o Only works for 512 elements (one thread block) GPU has a complexity of O(nlog 2 n) ( CPU version is O(n) )

A work efficient parallel scan o o Goal is a parallel scan that is O(n) instead of O(nlog 2 n) Solution: Balanced Trees: Build a binary tree on the input data and sweep it to and from the root. Binary tree with n leaves has d=log 2 n levels, each level d has 2 d nodes One add is performed per node, therefore O(n) add on a single traversal of the tree. n

Balanced Binary Trees Binary tree with n leaves has d=log 2 n levels, each level d has 2 d nodes One add is performed per node, therefore O(n) add on a single traversal of the tree. Two Phase Algorithm 1. Up-sweep phase 2. Down-sweep phase d=0 d=1 d=2 d=3 Tree for n = 8

The Up-Sweep Phase for(d = 1; d < log 2 n-1; d++) for all k=0; k < n-1; 2 d+1 in parallel x[k+2 d+1 -1] = x[k+2 d-1] + x[k+2 d+1 -1] Where have we seen this before?

The Down-Sweep Phase x[n-1] = 0; for(d = log 2 n – 1; d >=0; d--) for all k = 0; k < n-1; k += 2 d+1 in parallel t = x[k + 2 d – 1] x[k + 2 d - 1] = x[k + 2 d+1 -1] x[k + 2 d+1 - 1] = t + x[k + 2 d+1 – 1] x 0 ∑(x 0. . x 1) x 2 ∑(x 0. . x 3) x 4 ∑(x 4. . x 5) x 6 ∑(x 0. . x 7) x 0 ∑(x 0. . x 1) x 2 ∑(x 0. . x 3) x 4 ∑(x 4. . x 5) x 6 0 x 0 ∑(x 0. . x 1) x 2 0 x 4 ∑(x 4. . x 5) x 6 ∑(x 0. . x 3) x 0 0 x 2 ∑(x 0. . x 1) x 4 ∑(x 0. . x 3) x 6 ∑(x 0. . x 5) 0 x 0 ∑(x 0. . x 1) ∑(x 0. . x 2) ∑(x 0. . x 3) ∑(x 0. . x 4) ∑(x 0. . x 5) ∑(x 0. . x 6)

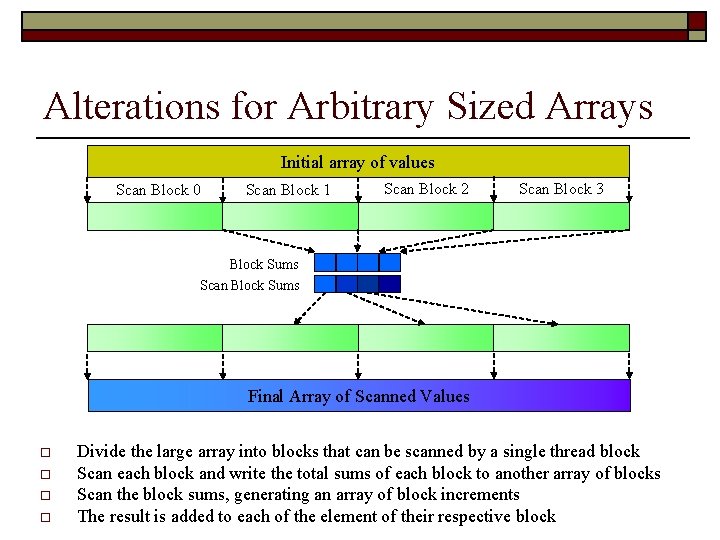
Current Limitations o o Array sizes are limited to 1024 elements Array sizes must be a power of two

Alterations for Arbitrary Sized Arrays Initial array of values Scan Block 0 Scan Block 1 Scan Block 2 Scan Block 3 Block Sums Scan Block Sums Final Array of Scanned Values o o Divide the large array into blocks that can be scanned by a single thread block Scan each block and write the total sums of each block to another array of blocks Scan the block sums, generating an array of block increments The result is added to each of the element of their respective block

Applications o o o Stream Compaction Summed-Area Tables Radix Sort

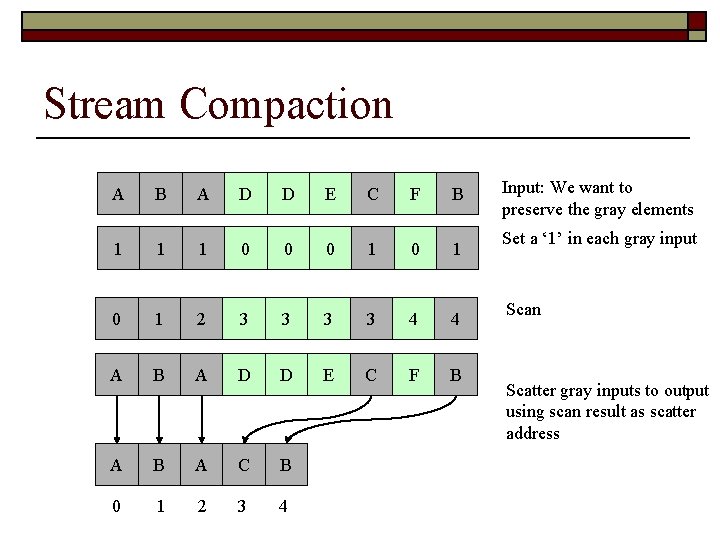
Stream Compaction Definition: n o Extracts the ‘interest’ elements from an array of elements and places them continuously in a new array Uses: n n Collision Detection Sparse Matrix Compression A B A D D A B A C B E C F B

Stream Compaction A B A D D E C F B 1 1 1 0 0 0 1 0 1 2 3 3 4 4 A B A D D E C F B A C B 0 1 2 3 4 Input: We want to preserve the gray elements Set a ‘ 1’ in each gray input Scan Scatter gray inputs to output using scan result as scatter address

Summed Area Tables o Definition: n o A 2 D table generated from an input image in which each entry in the table stores the sum of all pixels between the entry location and the lowerleft corner of the input image Uses: n Can be used to perform filters of different widths at every pixel in the image in constant time per pixel

Summed Area Tables 1. 2. 3. Apply sum scan to all rows of the image Transpose image Apply a sum scan to all rows of the result

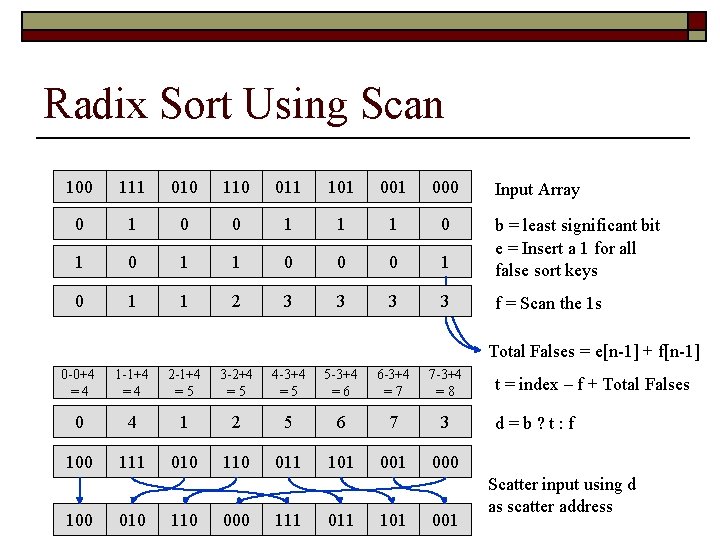
Radix Sort Initial Array 110011 51 101001 41 010011 19 000110 6 110000 48 011001 25 010111 23 Pass 1 Pass 2 000110 6 110000 48 110011 51 101001 41 010011 19 011001 25 010111 23 110000 48 101001 41 011001 25 000110 6 110011 51 010011 19 010111 23 Pass 4 Pass 5 000110 6 101001 41 110000 48 110011 51 010011 19 010111 23 011001 25 000110 6 010011 19 010111 23 011001 25 101001 41 110000 48 110011 51 Pass 3 110000 48 101001 41 011001 25 110011 51 010011 19 000110 6 010111 23 110000 48 110011 51 010011 19 000110 6 010111 23 101001 41 011001 25

Radix Sort Using Scan 100 111 010 110 011 101 000 0 1 1 1 0 0 0 1 b = least significant bit e = Insert a 1 for all false sort keys 0 1 1 2 3 3 f = Scan the 1 s Input Array Total Falses = e[n-1] + f[n-1] 0 -0+4 =4 1 -1+4 =4 2 -1+4 =5 3 -2+4 =5 4 -3+4 =5 5 -3+4 =6 6 -3+4 =7 7 -3+4 =8 0 4 1 2 5 6 7 3 100 111 010 110 011 101 000 100 010 110 000 111 011 101 001 t = index – f + Total Falses d=b? t: f Scatter input using d as scatter address

Radix Sort Using GPU o o o Partial Radix sort is performed once for each block. Scan needs to be performed once for each bit Partial sorts are then sorted together using bitonic sort

References o These slides are directly based upon the following resource and are meant for education purposes only. GPU Gems III, Chapter 39, Parallel Prefix Sum (Scan) with CUDA, Mark Harris, Shubhabrata Sengupta, John D. Owens