1 A quadratic equation is an equation equivalent










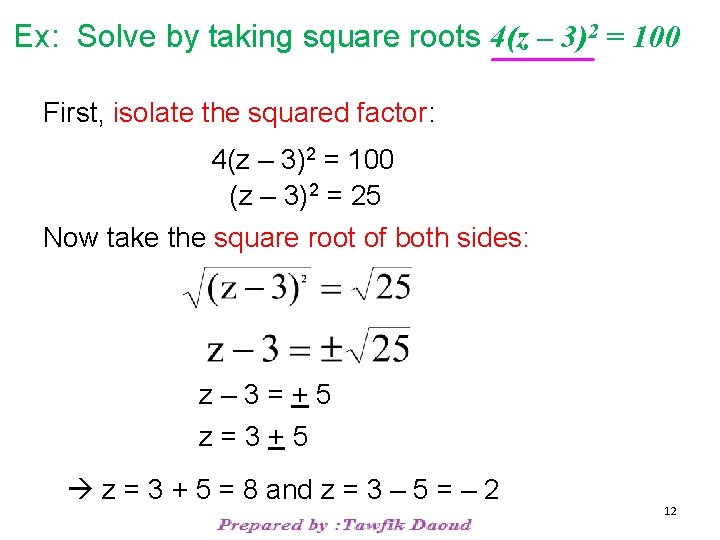



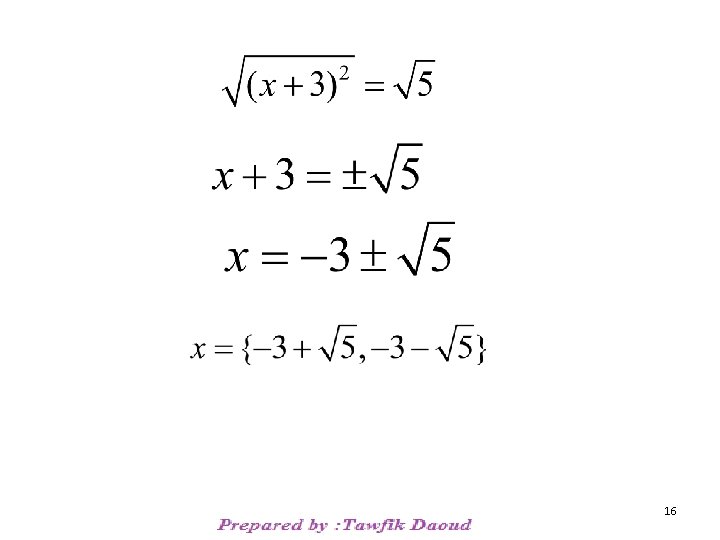




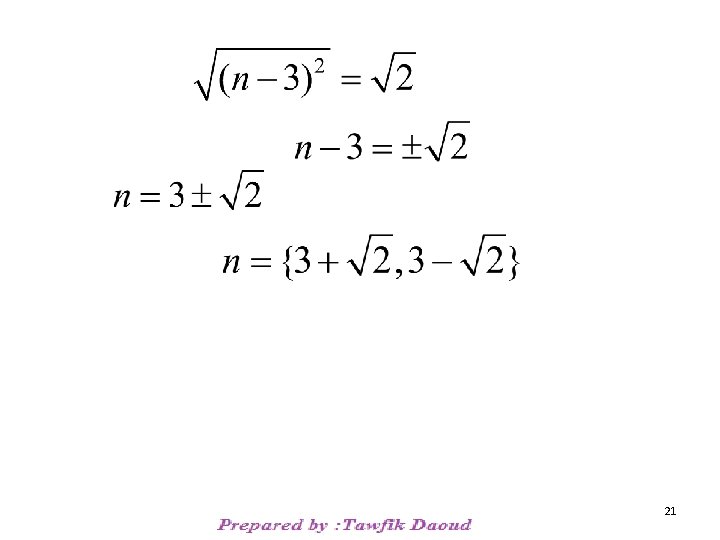















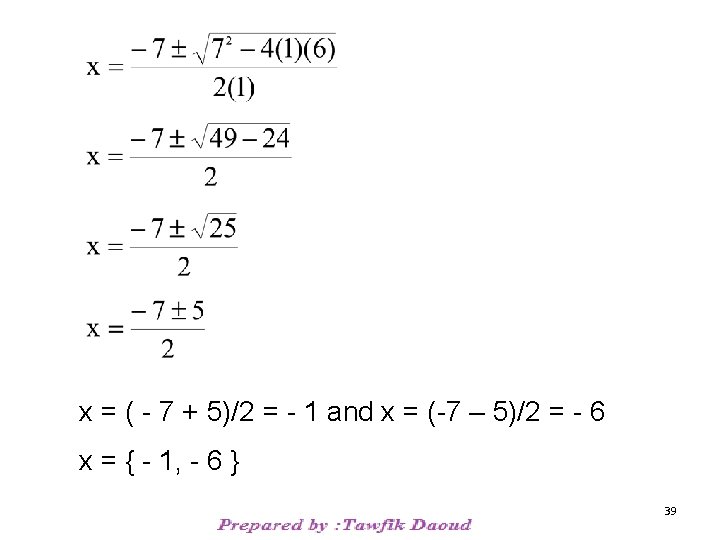

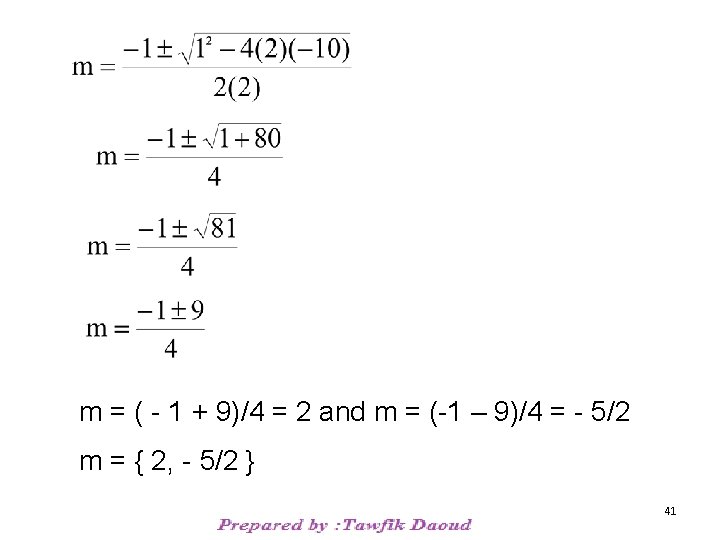













- Slides: 54

1

A quadratic equation is an equation equivalent to one of the form Where a, b, and c are real numbers and a 0 So if we have an equation in x and the highest power is 2, it is quadratic. To solve a quadratic equation we get it in the form above and see if it will factor. -5 x + 6 Get form above by subtracting 5 x and adding 6 to both sides to get zero on right side. Factor of 6 {1, 6 or 2, 3} Use the Null Factor law and set each factor = 0 and solve. 2

Remember standard form for a quadratic equation is: In this form we could have the case where b = 0. When this is the case, we get the x 2 alone and then square root both sides. +6 2 +6 Get x 2 alone by adding 6 to both sides and then dividing both sides by 2 2 Now take the square root of both sides remembering that you must consider both the positive and negative root. Let's check: 3

What if in standard form, c = 0? We could factor by pulling an x out of each term. Factor out the common x Use the Null Factor law and set each factor = 0 and solve. 4

Solving Quadratic Equations by Factoring Example 5

Example 6

Example 7

Example 8

Example 9

Solving Quadratic Equations by square roots An alternate method of solving a quadratic equation is using the Principle of Taking the Square Root of Each Side of an Equation If x 2 = a, then x=+ 10

Ex: Solve by taking square roots 3 x 2 – 36 = 0 First, isolate x 2: 3 x 2 – 36 = 0 3 x 2 = 36 x 2 = 12 Now take the square root of both sides: 11
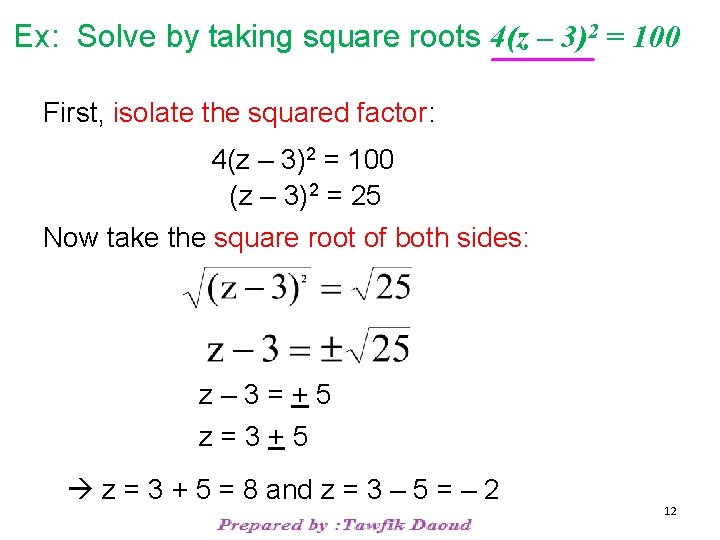
Ex: Solve by taking square roots 4(z – 3)2 = 100 First, isolate the squared factor: 4(z – 3)2 = 100 (z – 3)2 = 25 Now take the square root of both sides: z– 3=+5 z=3+5 z = 3 + 5 = 8 and z = 3 – 5 = – 2 12

Ex: Solve by taking square roots 5(x + 5)2 – 75 = 0 First, isolate the squared factor: 5(x + 5)2 = 75 (x + 5)2 = 15 Now take the square root of both sides: 13

Steps to solving Quadratic Equations by Completing the Square 14

Ex: Solve x 2 + 6 x + 4 = 0 by completing the square First, rewrite the equation with the constant on one side of the equals and a lead coefficient of 1. x 2 + 66 x = – 4 b= 6 x 2 + 6 x + 9 = – 4 + 9 x 2 + 6 x + 9 = 5 (x + 3)2 = 5 Now take the square root of both sides 15
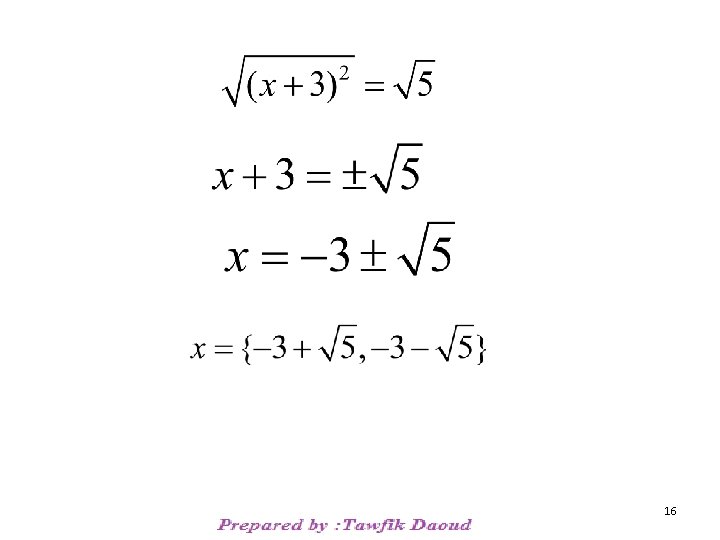
16

solve by completing the square. 2 2 To complete the square we want the coefficient of the x 2 term to be 1. Divide everything by 2 16 16 Since it doesn't factor get the constant on the other side ready to complete the square. So what do we add to both sides? the middle term's coefficient divided by 2 and squared Factor the left hand side Add 4 to both sides to get x alone 17

Ex: Solve 2 y 2 = 3 – 5 y by completing the square First, rewrite the equation with the constant on one side of the equals and a lead coefficient of 1. 2 y 2 + 5 y = 3 y 2 + (5/2)y = (3/2) Add [½(b)]2 to both sides: b = 5/2 [½(5/2)]2 = (5/4)2 = 25/16 y 2 + (5/2)y + 25/16 = (3/2) + 25/16 y 2 + (5/2)y + 25/16 = 24/16 + 25/16 (y + 5/4)2 = 49/16 Now take the square root of both sides 18


Ex: Solve 3 n– 5 = (n – 1)(n – 2) Is this a quadratic equation? 3 n – 5 = n 2 – 2 n – n + 2 3 n – 5 = n 2 – 3 n + 2 n 2 – 6 n + 7 = 0 n 2 – 6 n = – 7 Collect all terms [½(-6)]2 = (-3)2 = 9 n 2 – 6 n + 9 = – 7 + 9 (n – 3)2 = 2 20
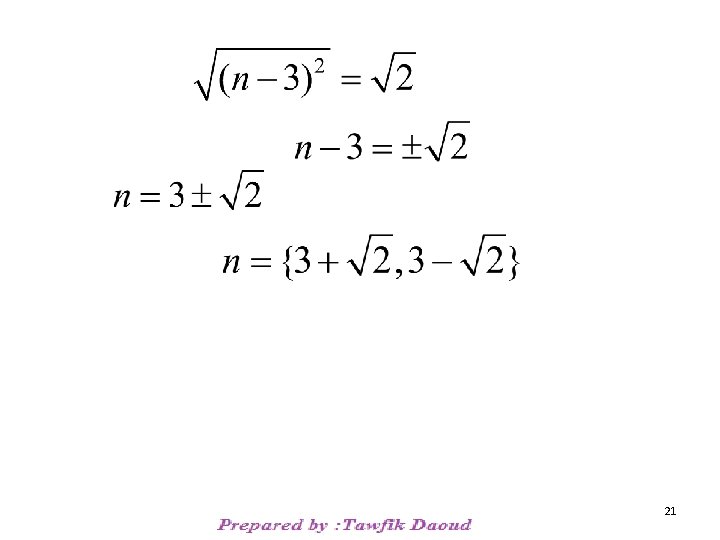
21

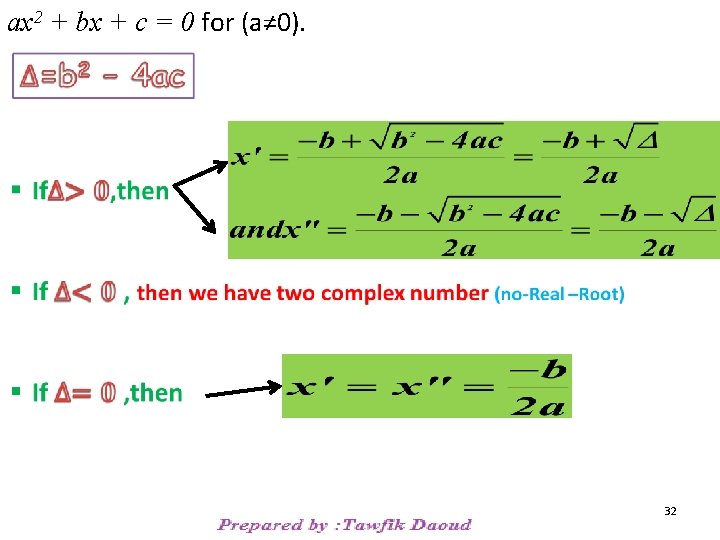
Solving Quadratic Equations by Quadratic Formula q. Consider a quadratic equation of the form ax 2 + bx + c = 0 for (a≠ 0). q. Completing the square 22

Solutions to ax 2 + bx + c = 0 for (a≠ 0) are: 23

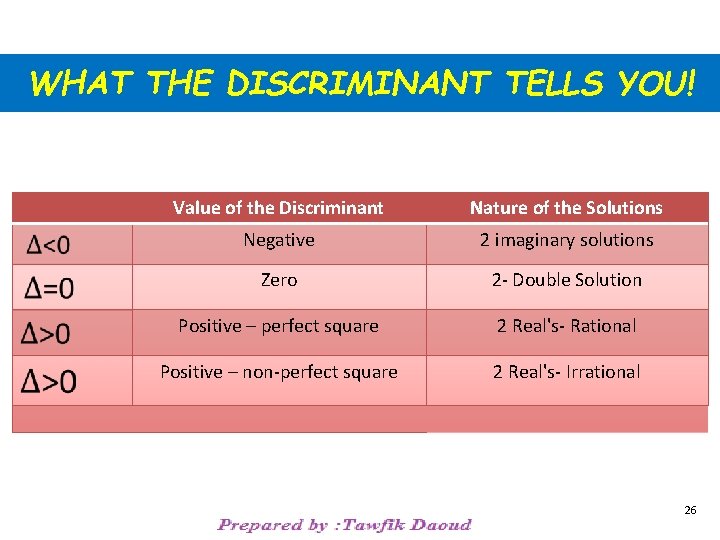
WHY USE THE QUADRATIC FORMULA? The quadratic formula allows you to solve any quadratic equation, even if you cannot factor it. An important piece of the quadratic formula is what’s under the radical: b 2 – 4 ac This piece is called the discriminant. 24

WHY IS THE DISCRIMINANT IMPORTANT? The discriminant will take on a value that is positive, 0, or negative. The value of the discriminant indicates two distinct real solutions, one real solution, or no real solutions, respectively. 25

WHAT THE DISCRIMINANT TELLS YOU! Value of the Discriminant Nature of the Solutions Negative 2 imaginary solutions Zero 2 - Double Solution Positive – perfect square 2 Real's- Rational Positive – non-perfect square 2 Real's- Irrational 26

Example Use the discriminant to determine the number and type of solutions for the following equation. 5 – 4 x + 12 x 2 = 0 a = 12, b = – 4, and c = 5 b 2 – 4 ac = (– 4)2 – 4(12)(5) = 16 – 240 = – 224<0 There are no real solutions. 27

Example 6 – 3 x 2 – 2 x = 0 a = – 3, b = – 2, and c = 6 b 2 – 4 ac = (– 2)2 – 4(– 3)(6) = 4 + 72 = 76>0 There are 2 distinct root. 28

Example x 2 – 4 x +4= 0 a = 1, b = – 4, and c = 4 b 2 – 4 ac = (– 4)2 – 4(1)(4) = 16 – 16 = 0 We have two double root 29

By completing the square on a general quadratic equation in standard form we come up with what is called the quadratic formula. This formula can be used to solve any quadratic equation whether it factors or not. If it factors, it is generally easier to factor---but this formula would give you the solutions as well. We solved this by completing the square but let's solve it using the quadratic formula 1 6 6 (1) (3) Don't make a mistake with order of operations! Let's do the power and the multiplying first. 30

There's a 2 in common in the terms of the numerator These are the solutions we got when we completed the square on this problem. NOTE: When using this formula if you've simplified under the radical and end up with a negative, there are no real solutions. (There are complex (imaginary) solutions, but that will be dealt with in year 12 Calculus). 31

ax 2 + bx + c = 0 for (a≠ 0). 32

If b is an even number in the quadratic Equation ax 2 + bx + c = 0 for (a≠ 0). 33

Sum and Product of the Root The sum of the roots of the Quadratic equation: ax 2 + bx + c = 0 is And the product of roots is This means that: 34

Note: Two numbers whose given sum is S and given product is P are roots of the equation x 2 - Sx + P= 0 Example: Find two numbers knowing their sum S and their product P : S=4 and P=4 The two required numbers are the solutions of the equation: x 2 - 4 x + 4= 0 , that is (x-2)2 =0, which gives x’=x”=2 35

Example • 36

Example Solve using the Quadratic Formula 37

Ex: Use the Quadratic Formula to solve x 2 + 7 x + 6 = 0 Recall: For quadratic equation ax 2 + bx + c = 0, the solutions to a quadratic equation are given by Identify a, b, and c in ax 2 + bx + c = 0: a=1 b= 7 c= 6 Now evaluate the quadratic formula at the identified values of a, b, and c 38
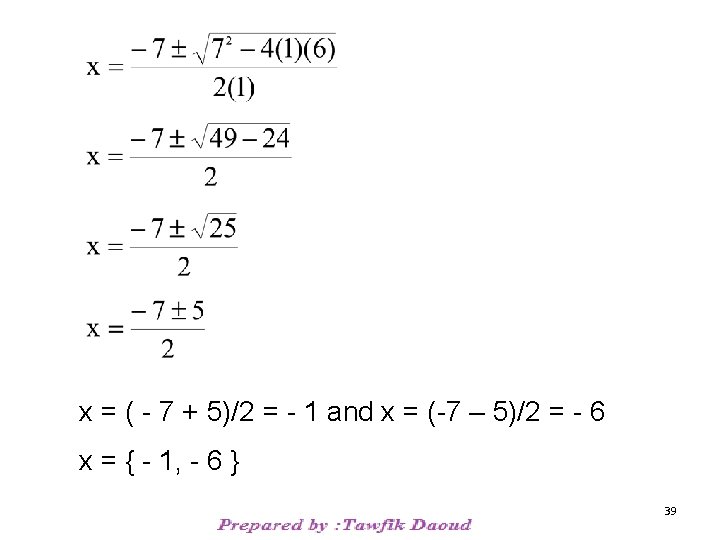

Ex: Use the Quadratic Formula to solve 2 m 2 + m – 10 = 0 Recall: For quadratic equation ax 2 + bx + c = 0, the solutions to a quadratic equation are given by Identify a, b, and c in am 2 + bm + c = 0: a=2 b= 1 c = - 10 Now evaluate the quadratic formula at the identified values of a, b, and c 40
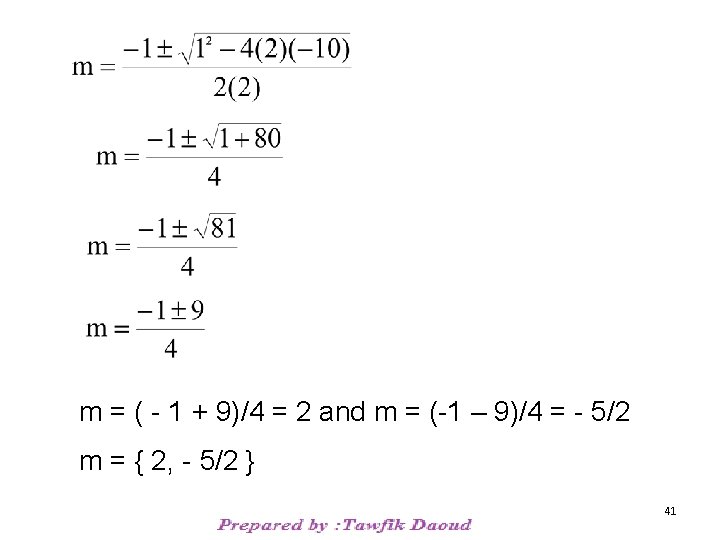

Example Solve 11 n 2 – 9 n = 1 by the quadratic formula. 11 n 2 – 9 n – 1 = 0, so a = 11, b = -9, c = -1 42

Example Solve x 2 + x – = 0 by the quadratic formula. x 2 + 8 x – 20 = 0 (multiply both sides by 8) a = 1, b = 8, c = 20 43

Example Solve x(x + 6) = 30 by the quadratic formula. x 2 + 6 x + 30 = 0 a = 1, b = 6, c = 30 So there is no real solution. 44

Example Solve 12 x = 4 x 2 + 4. 0 = 4 x 2 – 12 x + 4 0 = 4(x 2 – 3 x + 1) Let a = 1, b = -3, c = 1 45

Example Solve the following quadratic equation. 46

Solving Quadratic Equations by the Quadratic Formula Try the following examples. Do your work on your paper and then check your answers. 47

Quadratic Equations and Problem Solving A cliff diver is 64 feet above the surface of the water. The formula for calculating the height (h) of the diver after t seconds is: How long does it take for the diver to hit the surface of the water? seconds 48

Quadratic Equations and Problem Solving The length of a rectangular garden is 5 feet more than its width. The area of the garden is 176 square feet. What are the length and the width of the garden? The width is w. The length is w+5. feet 49

Quadratic Equations and Problem Solving Find two consecutive odd numbers whose product is 23 more than their sum? Consecutive odd numbers: 50

Quadratic Equations and Problem Solving The length of one leg of a right triangle is 7 meters less than the length of the other leg. The length of the hypotenuse is 13 meters. What are the lengths of the legs? meters 51

Quadratic Equations and Problem Solving The square of a number minus twice the number is 63. Find the number. x is the number. 52

SUMMARY OF SOLVING QUADRATIC EQUATIONS • Get the equation in standard form: • If there is no middle term (b = 0) then get the x 2 alone and square root both sides (if you get a negative under the square root there are no real solutions). • If there is no constant term (c = 0) then factor out the common x and use the null factor law to solve (set each factor = 0). • If a, b and c are non-zero, see if you can factor and use the null factor law to solve. • If it doesn't factor or is hard to factor, use the quadratic formula to solve (if you get a negative under the square root there are no real solutions). 53

This "discriminates" or tells us what type of solutions we'll have. If we have a quadratic equation and are considering solutions from the real number system, using the quadratic formula, one of three things can happen. 1. The "stuff" under the square root can be positive and we'd get two unequal real solutions 2. The "stuff" under the square root can be zero and we'd get one solution (called a repeated or double root because it would factor into two equal factors, each giving us the same solution). 3. The "stuff" under the square root can be negative and we'd get no real solutions. The "stuff" under the square root is called the discriminant. 54