Nature of Roots Nature of Roots Quadratic Equation

Nature of Roots

Nature of Roots Quadratic Equation: ax 2 + bx + c = 0 ; a 0 Discriminant = = b 2 – 4 ac >0 Two unequal real roots =0 One double real root (Two equal real roots) <0 No real roots Note: 0 Real roots

Transformation of a graph

Translation The original graph is y = f(x). Let h, k > 0. Graph Transformation Description y = f(x) + k Translation The graph y = f(x) + k is obtained by translating the graph along the y-axis of y = f(x) k units upwards. y = f(x) k Translation The graph y = f(x) k is obtained by translating the graph along the y-axis of y = f(x) k units downwards. y = f(x – h) Translation The graph y = f(x – h) is obtained by translating the graph along the x-axis of y = f(x) h units to the right. y = f(x + h) Translation The graph y = f(x + h) is obtained by translating the graph along the x-axis of y = f(x) h units to the left.

Translation Examples Graph Transformation Description y = f(x) + 3 Translation The graph y = f(x) + 3 is obtained by translating the graph along the y-axis of y = f(x) 3 units upwards. y = f(x) 3 Translation The graph y = f(x) 3 is obtained by translating the graph along the y-axis of y = f(x) 3 units downwards. y = f(x – 2) Translation The graph y = f(x – 2) is obtained by translating the graph along the x-axis of y = f(x) 2 units to the right. y = f(x + 2) Translation The graph y = f(x + 2) is obtained by translating the graph along the x-axis of y = f(x) 2 units to the left.

Reflection The original graph is y = f(x). Graph Transformation Description y = f( x) Reflection about The graph y = f( x) is obtained by reflecting the graph of the y-axis y = f(x) about the y-axis. y = f(x) Reflection about The graph y = f(x) is obtained by reflecting the graph of the x-axis y = f(x) about the x-axis.

Reflection Examples Graph Transformation Description y = 2 x Reflection about The graph y = 2 x is obtained by reflecting the graph of the y-axis y = 2 x about the y-axis. y = 2 x Reflection about The graph y = 2 x is obtained by reflecting the graph of the x-axis y = 2 x about the x-axis.

Enlargement and Reduction The original graph is y = f(x). Graph Transformation Description y = kf(x) , k>1 Enlargement The graph of y = kf(x) is obtained by enlarging to k times along the y-axis the graph of y = f(x) along the y-axis. y = kf(x) , k<1 Reduction along The graph of y = kf(x) is obtained by reducing to k of the y-axis graph of y = f(x) along the y-axis. y = f(kx) , k>1 Reduction along The graph of y = f(kx) is obtained by reducing to 1/k of the x-axis the graph of y = f(x) along the x-axis. y = f(kx) , k<1 Enlargement The graph of y = f(kx) is obtained by enlarging to 1/k along the x-axis times of the graph of y = f(x) along the x-axis.

Enlargement and Reduction Examples Graph Transformation Description y = 2 f(x) Enlargement The graph of y = 2 f(x) is obtained by enlarging to 2 times along the y-axis the graph of y = f(x) along the y-axis. y = f(x) Reduction along The graph of y = f(x) is obtained by reducing to 1/2 of the y-axis the graph of y = f(x) along the y-axis. y = f(2 x) Reduction along The graph of y = f(2 x) is obtained by reducing to 1/2 of the x-axis the graph of y = f(x) along the x-axis. y = f( x) Enlargement The graph of y = f( x) is obtained by enlarging to 2 times along the x-axis of the graph of y = f(x) along the x-axis.

Trigonometric Functions

Trigonometric Functions of Special Angles (I) 0 sin 30 45 0 60 90 1 30 2 2 60 cos 1 tan 0 0 1 1 undefined 1 45 1

Trigonometric Functions of Special Angles (II) (0, 1) ( 1, 0) (0, 1) 1 0 sin 1 0 0 1 cos 0 undefined 1 0 tan undefined 0

Trigonometric Functions of General Angles (I) S T II I III IV A C

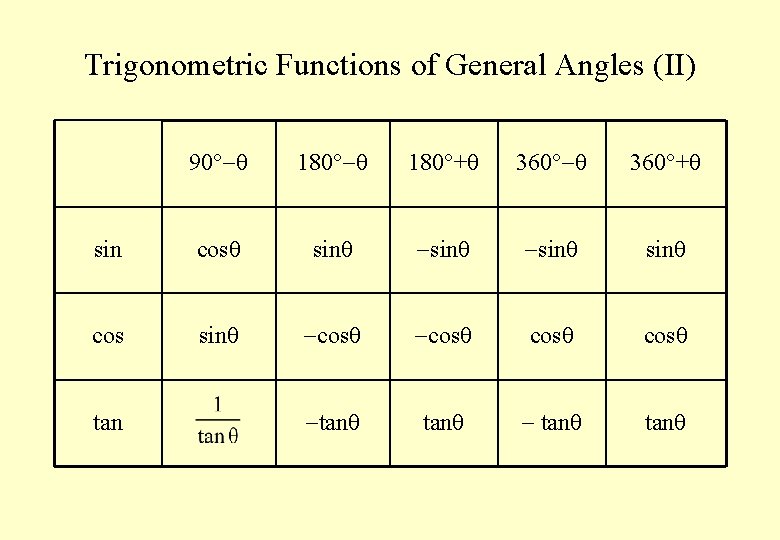
Trigonometric Functions of General Angles (II) 90 180 + 360 + sin cos sin cos sin cos tan tan

Nets of a cube

Nets of a cube Two nets are identical if one can be obtained from the other from rotation (turn it round) or/and reflection (turn it over). An example of identical nets.

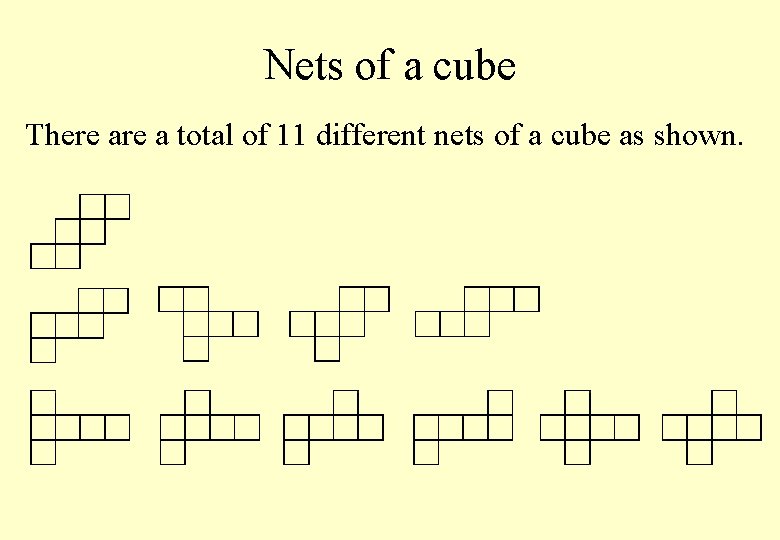
Nets of a cube There a total of 11 different nets of a cube as shown.

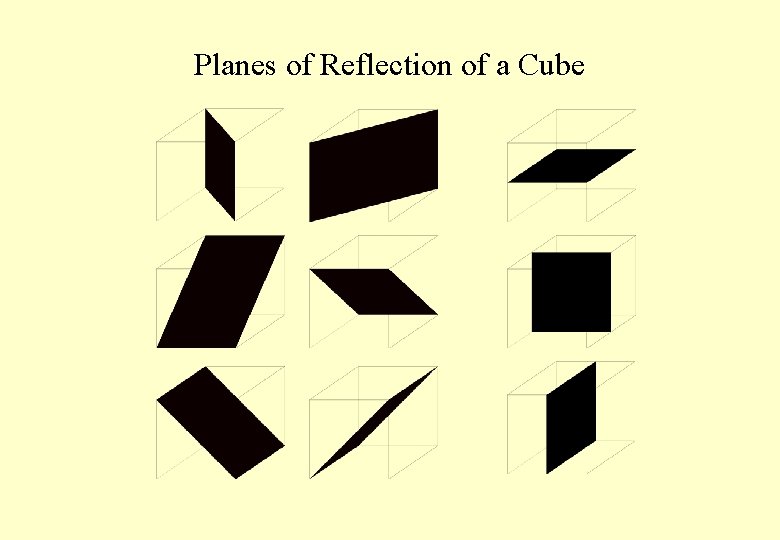
Planes of Reflection

Planes of Reflection of a Cube

Planes of Reflection of a Regular Tetrahedron

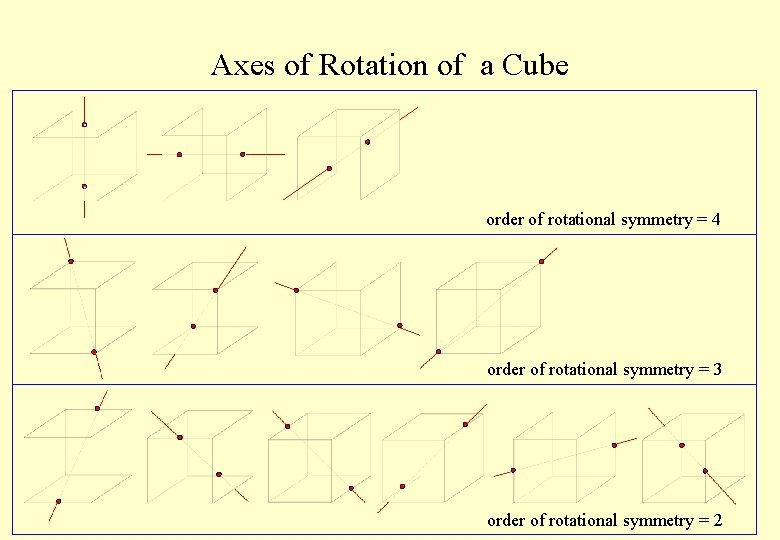
Axes of Rotation

Axes of Rotation of a Cube order of rotational symmetry = 4 order of rotational symmetry = 3 order of rotational symmetry = 2

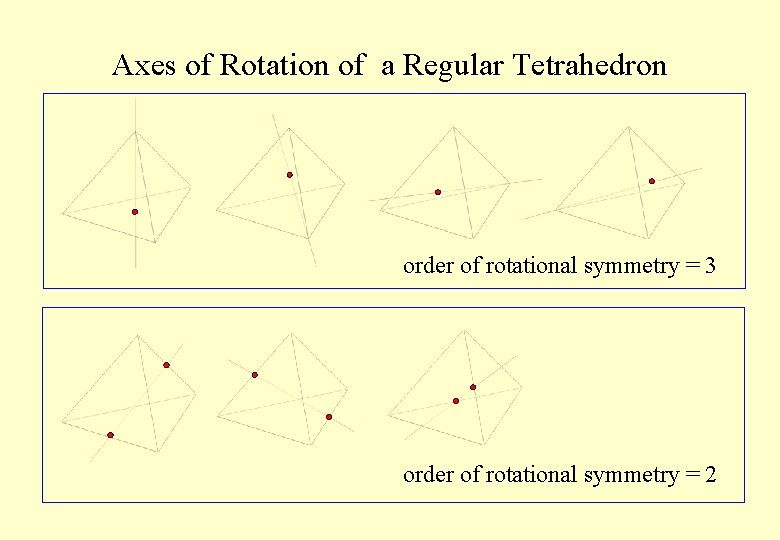
Axes of Rotation of a Regular Tetrahedron order of rotational symmetry = 3 order of rotational symmetry = 2

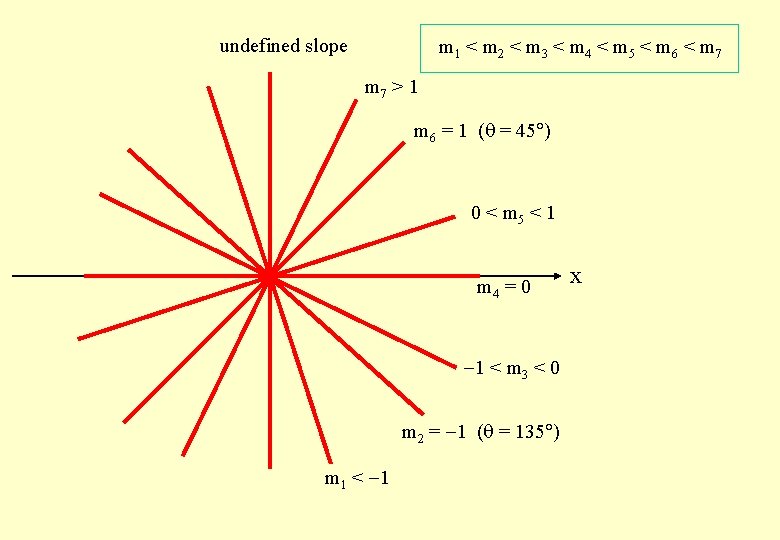
Compare Slopes of Different Lines

undefined slope m 1 < m 2 < m 3 < m 4 < m 5 < m 6 < m 7 > 1 m 6 = 1 ( = 45 ) 0 < m 5 < 1 m 4 = 0 1 < m 3 < 0 m 2 = 1 ( = 135 ) m 1 < 1 x