VIII Funktsiooni piirvrtus ja tuletis Taimi TammVask Phioskused

VIII Funktsiooni piirväärtus ja tuletis. Taimi Tamm-Vask

Põhioskused. Funktsiooni piirväärtuse leidmine lihtsamatel juhtudel. Funktsiooni tuletise leidmine. Funktsiooni kasvamis- ja kahanemisvahemike leidmine. Funktsiooni graafiku maksimum- ja miinimumpunktide leidmine. Ekstreemumülesannete lahendamine. Funktsiooni graafiku puutuja võrrandi leidmine antud punktis, puutuja joonestamine. Lihtsamate funktsioonide uurimine tuletise abil ja nende graafiku skitseerimine. 2

Funktsioonide piirväärtus. Funktsioonide y = f(x) ja y = g(x) korral: 3

Kaks olulist piirväärtust. 4

Tuletis. Funktsiooni y = f (x) muut Funktsiooni y = f(x) tuletis 5

Tuletiste tabel 6

Tuletiste tabel 7

Tuletiste tabel 8

Tuletiste tabel 9

Tuletiste tabel 10

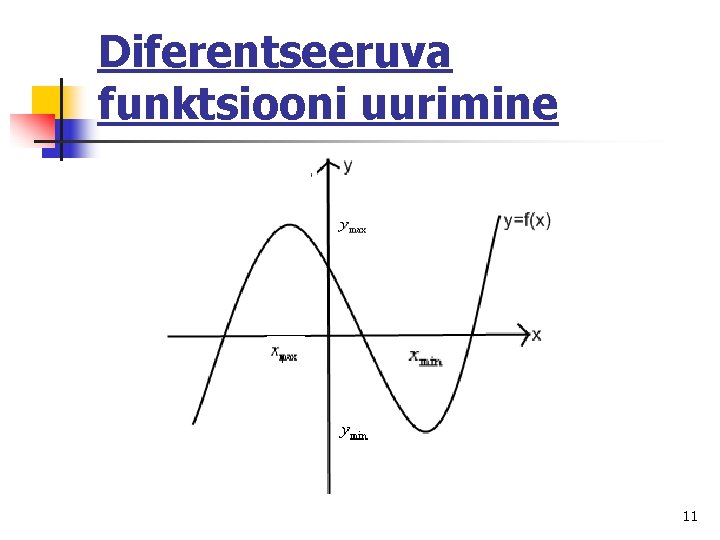
Diferentseeruva funktsiooni uurimine 11

Diferentseeruva funktsiooni uurimine Funktsiooni y = f(x) kasvamispiirkonna kahanemispiirkonna moodustavad kõik need argumendi x väärtused, mis on võrratuse lahendid. 12

Diferentseeruva funktsiooni uurimine Funktsiooni graafiku punkte, milles funktsiooni kasvamine läheb üle kahanemiseks või vastupidi, nimetatakse ekstreemumpunktideks ja vastava punkti abstsissi väärtust ekstreemumkohaks ning ordinaadi väärtust funktsiooni ekstreemumiks. 13

Maksimumpunktiks nimetatakse funktsiooni ekstreemumpunkti, milles kasvamine läheb üle kahanemiseks. Miinimumpunktiks nimetatakse ekstreemumpunkti, milles funktsiooni kahanemine läheb üle kasvamiseks. 14

Funktsioon võib omada ekstreemumit kohal, kus tema tuletis võrdub nulliga või kus tal tuletis puudub. Funktsiooni ekstreemumkohtade leidmiseks tuleb leida tuletise nullkohad s. o lahendada võrrand ja kohad, kus tuletis puudub. 15

Kui leitud kohal funktsiooni tuletis muudab märki, siis on tegemist ekstreemumkohaga. Kui tuletis märki ei muuda, siis funktsioonil pole sellel kohal ekstreemumit. 16

Maksimumkoht Miinimumkoht 17

Funktsiooni maksimum Funktsiooni miinimum 18

Kui funktsiooni ekstreemumit otsitakse mingil lõigul, tuleb eespool märgitud argumendi väärtustele vaatluse alla võtta ka lõigu otspunktid. Kõigi saadud argumendi väärtuste korral arvutatakse vastavad funktsiooni väärtused ning viimaste seast leitakse vastavalt vajadusele kas suurim või vähim. 19

Funktsiooni kumerusvahemike leidmiseks tuleb lahendada võrratus Nõgususvahemike leidmiseks tuleb lahendada võrratus 20

Graafiku selliseid punkte, kus funktsioon on diferentseeruv ja tema graafiku kumerus asendub nõgususega või vastupidi, nimetatakse käänupunktideks. Nende punktide abstsisse nimetatakse käänukohtadeks. Funktsiooni käänukohtade leidmiseks tuleb lahendada võrrand 21

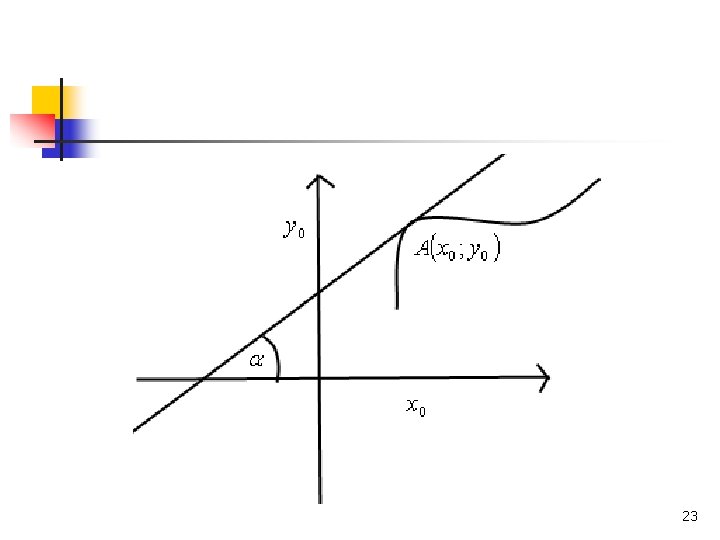
Funktsiooni graafiku puutuja. Funktsiooni y = f(x) graafiku puutuja punktis on sirge Milles puutuja tõus on puutuja tõusunurk. Kui on antud ja puutepunkt on , siis 22

23