Funktsiooni esitusviisid Urve Paulmann 2009 Funktsiooni esitusviisid n

Funktsiooni esitusviisid Urve Paulmann 2009

Funktsiooni esitusviisid n n n analüütiline esitus (valemi abil) tabeli abil arvupaaridena graafiku abil nooldiagrammina sõnaline formuleering

Valem n n n võrdus, mille kohaselt on vastavalt x väärtusele võimalik arvutada y väärtust milliseid tehteid ja millises järjekorras tuleb argumendi väärtusega teha, et saada vastav funktsiooni väärtus seni kõige enim kasutatav funktsiooni esitusviis

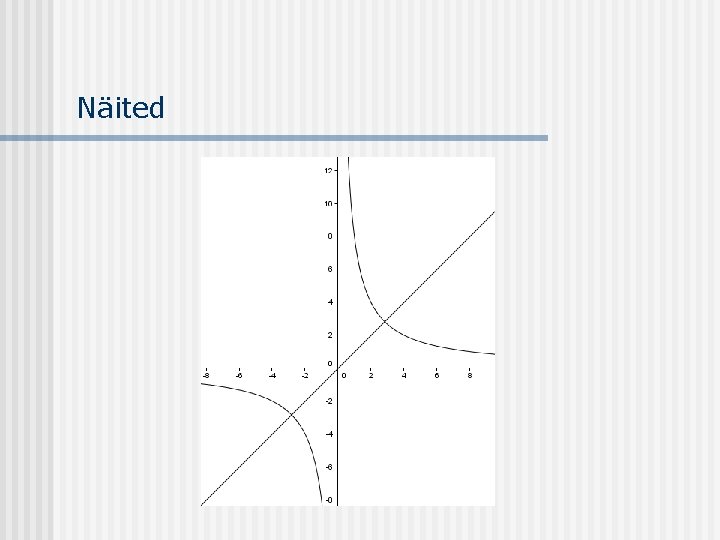
Näited n n y = 3 x – 1 on lineaarfunktsioon võrdus y = 1/x esitab pöördvõrdelist sõltuvust s = vt on teepikkuse valem funktsioon võib olla esitatud ka mitme valemiga

Tabel n n n ühes reas (või veerus) argumendi x väärtused, teises reas (veerus) sellele vastavad funktsiooni väärtused astmete, juurte ja trigonomeetriliste funktsioonide tabelid mõnikord polegi funktsiooni esitamiseks muud võimalust peale tabeli

Näited n n praktikas leitakse sageli suuruste vaheline sõltuvus katseliselt eksperimendi käigus saadud tulemused auto sõidukiiruse ja bensiinikulu vahel Kiirus km/h Bensiini kulu l 30 60 11 9 80 100 120 10 11 12

Arvupaarid n n kõikvõimalikud järjestatud arvupaarid, milles esimesel kohal on argumendi väärtus ja teisel kohal sellele vastav funktsiooni väärtus näiteks: on antud funktsioon y = Ix. I, kus X = {-2; -1; 0; 1; 2}. See funktsioon avaldub arvupaaridena järgmiselt: {(-2; 2), (-1; 1), (0; 0), (1; 1), (2; 2)}

Graafik n n funktsiooni f graafikuks on joon, mille võrrand on y = f(x) saab olla vaid selline joon, mille korral igale x väärtusele vastab vaid üks punkt sellel joonel koordinaatteljestikus võimalik kujutada vaid osa graafikust võib koosneda kas üksikutest punktidest, pidevast joonest või mitmest pidevast joonest

Graafik n n n võimaldab funktsiooni kujutada piltlikumalt funktsiooni mitmed omadused selgemini nähtavad kui valemist eksperimentaalteadustes väga levinud seoste esitamisviis

Näited

Nooldiagramm n n n esitatakse kahe hulgana, millest üks neist kujutab funktsiooni määramispiirkonda, teine muutumispiirkonda seoseid hulkade vahel kujutatakse noolte abil argumendi igale väärtusele vastab funktsiooni väärtus neid väärtusi oleks argumendi iga väärtuse jaoks vaid üks hulga X iga elemendi juurest peab lähtuma täpselt üks nool

Näited n Näide 1 Igal inimesel on teatav vanus. Seega igale inimesele saame vastavusse seada ühe arvu – tema vanuse. Inimese “vanus” on funktsioon, mille määramispiirkonnaks on inimeste hulk ja muutumispiirkonnaks arvude hulk. Mart Mai Anu 35 28 22

Näited n Näide 2 Olgu määramispiirkonnaks inimeste hulk ja muutumispiirkonnaks riikide hulk. Kas “kodakondsus” on funktsioon? Kodakondsus ei ole funktsioon, sest leidub inimesi, kellel on mitme riigi kodakondsus, kuid on ka kodakondsuseta isikuid. Vene Lepp Al Ibn Sarah Mc. Donalds Eesti Kanada Somaalia

Sõnaline formuleering n n Dirichle`t funktsiooni pole võimalik esitada graafiku abil, vaid defineeritakse sõnalise formuleeringu abil arvu täisosa leidmine : arvu x täisosa on suurim täisarv, mis ei ületa arvu x

Kokkuvõte n n n enim kasutatav funktsiooni esitusviis on valem mõnikord polegi funktsiooni esitamiseks muud võimalust peale tabeli graafiku konstrueerimisel on saadud tulemus sageli ebatäpne, mistõttu lisatakse graafikule ka see reegel, mille abil leitakse need graafiku punktid (e. valem) leidub funktsioone, mille graafikut pole võimalik esitada kooskasutamine: valem, tabel, graafik

Kodune ülesanne n n n Selgita, kas järgmine seos määrab funktsiooni: - inimese vanus ja tema kehakaal - juhuslik täisarv ja selle ruutjuur - ringi raadius ja ringi pindala Miks ei saa Dirichle´t funktsiooni graafikuna esitada? Too näide iga funktsiooni esitusviisi kohta