UN SISTEMA DE DEDUCCIN NATURAL PARA EL CLCULO





































- Slides: 38

UN SISTEMA DE DEDUCCIÓN NATURAL PARA EL CÁLCULO PROPOSICIONAL Dr. Pedro Arturo Ramos Villegas l Academia de Filosofía, UACM Colegio de Filosofía, FFy. L, UNAM l parv@servidor. unam. mx l l

ANTECEDENTES Una primera versión del sistema de reglas de deducción natural para el cálculo proposicional que presento a continuación fue elaborada por los profesores Raúl Orayen, Arturo Yáñez y yo en la primera mitad de la década de los 90 s. Hasta la fecha no he sabido de alguien más que proponga un sistema similar a aquél. Ø La elaboración de ese sistema obedecía a objetivos didácticos y prácticos. Ø El sistema que presento a continuación pretende mejorar el sistema original atendiendo a los mismos objetivos. Ø

OBJETIVOS DEL SISTEMA EN LO DIDÁCTICO Está diseñado expresamente para facilitar la enseñanza y el aprendizaje de las reglas del cálculo proposicional, al clasificarlas en cinco grupos atendiendo a sus propiedades lógicas y su utilidad; a diferencia de las presentaciones tradicionales, que las clasifican únicamente en dos grupos, como reglas de implicación y reglas de equivalencia, atendiendo sólo a su forma lógica. Ø EN LO PRÁCTICO: Ø Está diseñado expresamente para facilitar el empleo de las reglas al efectuar deducciones, justo debido a sus ventajas didácticas. Ø Ø

VENTAJAS DIDÁCTICAS DEL SISTEMA Ø El sistema está diseñado expresamente para facilitar la enseñanza y el aprendizaje de la lógica proposicional, debido básicamente a dos aspectos: 1. Debido al modo peculiar en que se expone y contextualiza dentro del sistema cada regla en particular, como ilustraremos a continuación.

VENTAJAS DIDÁCTICAS DEL SISTEMA 2. Debido a que anexo a cada grupo de reglas se incluyen dos conjuntos de ejercicios. Uno diseñado para el grupo mismo y otro para la conjunción de ese grupo con los anteriores que ya hayan sido expuestos. De modo que al final de la exposición del sistema el alumno adquiere los siguientes saberes prácticos: l Sabe para qué sirve cada regla, en particular, y cómo articular ese saber práctico dentro del manejo del grupo al que la regla pertenece y, más en general, dentro del manejo del sistema en el que ésta se inserta. l Es capaz de realizar inferencia con todas las reglas de manera fluida.

ASPECTOS QUE SE CONSIDERAN EN LA EXPOSICIÓN DE CADA REGLA Ø 1. 2. 3. 4. 5. Hay seis aspectos de cada regla que se consideran dentro del sistema. Veamos un ejemplo: Nombre: Doble Negación. Abreviatura: DN. Presentación formal: A A. Lectura estructural: Una fórmula equivale a su doble negación. Prueba de validez: A A A v v vf f v fv

ASPECTOS QUE SE CONSIDERAN EN LA EXPOSICIÓN DE CADA REGLA 6. Utilidad: l Individual: Permite introducir o eliminar el signo de negación en fórmulas o subfórmulas individuales. l Grupal: Misma que la anterior, dado que el grupo de reglas al que pertenece incluye una sola regla. l Sistémica: Es auxiliar de todas aquellas reglas que incluyen negación.

REGLA AUXILIAR 1. Doble Negación (DN) A A

I. REGLAS DE IMPLICACIÓN PARA LA CONJUNCIÓN Y LA DISYUNCIÓN 2. Conjunción (Conj) A B______ / A B 3. Simplificación (Simp) A B / A 4. Adición (Ad) A______ / A B 5. Silogismo Disyuntivo (SD) A B A __ / B

II. REGLAS DE IMPLICACIÓN PARA EL CONDICIONAL 6. Modus Ponens (MP) A B A____ / B 8. Silogismo Hipotético (SH) A B B C___ / A C 7. Modus Tollens (MT) A B B___ / A

III. REGLAS DE EQUIVALENCIA PARA LA CONJUNCIÓN Y LA DISYUNCIÓN 9. Conmutación (Conm) 10. Asociación (Asoc) (A B) (B A) [A (B C)] [(A B) C] 11. Idempotencia (Idem) 12. Distribución (Dist) A (A A) [A (B C)] [(A B) (A C)]

IV. REGLAS DE EQUIVALENCIA PARA EL CONDICIONAL 13. Transposición (Tr) ( A B) ( B A) 14. Exportación (Exp) (A B) C] [A (B C)] 15. Distribución del Condicional (DC) [(A B) C)] [(A C) (B C)] [A (B C)] [(A B) (A C)]

V. REGLAS DE TRADUCCIÓN 16. Leyes de Morgan (de M) 17. Implicación Material(IM) (A B ) ( A B ) (A B ) ( A B ) (A B ) 18. Equivalencia Material (EM) 19. Ley Expansiva Fundamental (LEF) (A B) [(A B) (B A)] A [(A B) (A B)] (A B) [(A B) ( A B)] A [(A B) (A B)]

ØGRACIAS POR SUS COMENTARIOS Y CRÍTICAS

CONDICIONALIZACIÓN Y REDUCCIÓN AL ABSURDO EN UN SISTEMA DE DEDUCCIÓN NATURAL PARA EL CÁLCULO PROPOSICIONAL Dr. Pedro Arturo Ramos Villegas l Academia de Filosofía, UACM Colegio de Filosofía, FFy. L, UNAM l parv@servidor. unam. mx l l

INTRODUCCIÓN Hace poco presenté ante el TDL un sistema de reglas de deducción natural para la lógica proposicional (LP), el cual modificaba un sistema anterior elaborado originalmente durante la primera mitad de la década de los 90 s por los profesores Raúl Orayen, Arturo González y el que esto escribe. Ø En lo que sigue, expondré los métodos de prueba condicional (PC) y de reducción al absurdo (RAA) dentro del sistema modificado. Ø

INTRODUCCIÓN Primero, presentaré informalmente ambos métodos. Luego, propondré demostraciones semánticas y sintácticas de validez para cada uno, mostrando las ventajas didácticas de las primeras sobre las segundas (estas últimas las desarrollaré dentro del sistema modificado). Por último, hablaré sobre la utilidad de estos métodos de prueba. Ø Debo aclarar que la exposición de ambos métodos es una elaboración mía, por lo que cualquier error lógico que contenga no debe atribuirse a los otros profesores mencionados. Ø

TRES MÉTODOS FORMALES DE PRUEBA: MD, PC Y RAA Los sistemas deductivos de LP suelen contar con tres tipos de métodos formales o sintácticos de demostración: el método directo (MD) y dos métodos indirectos, la PC y la RAA. Ø El MD consiste en deducir una conclusión a partir de un conjunto dado de premisas usando sólo ese conjunto de premisas y las reglas de deducción habituales (conjunción, adición, etc. ). Ø Los métodos indirectos operan sumando premisas extra al conjunto original de premisas y deduciendo, con el auxilio de las reglas habituales, no directamente la conclusión, sino otras fórmulas (de las que la conclusión deseada es deducible en cualquier caso). Ø

DESCRIPCIÓN INFORMAL DE LA PC Y LA RAA La PC opera añadiendo como premisa extra el antecedente de un condicional que se desea demostrar y deduciendo su consecuente (del cual es deducible el condicional usando básicamente adición e implicación material). Ø La RAA opera añadiendo como premisa extra lo contradictorio de lo que se desea demostrar y deduciendo a partir de ello una contradicción cualquiera (de la cual es deducible la conclusión usando básicamente adición y silogismo disyuntivo). Ø

DEMOSTRACIÓN SEMÁNTICA DE LA PC Si P 1, P 2, …, Pn son las fórmulas-premisa de un argumento cualquiera y A B su fórmulaconclusión, entonces Ø No es posible que: P 1 = v P 2 = v. . . . Pn ___ _ = v Pn = v / A B = f A___ = v / B = f Ø

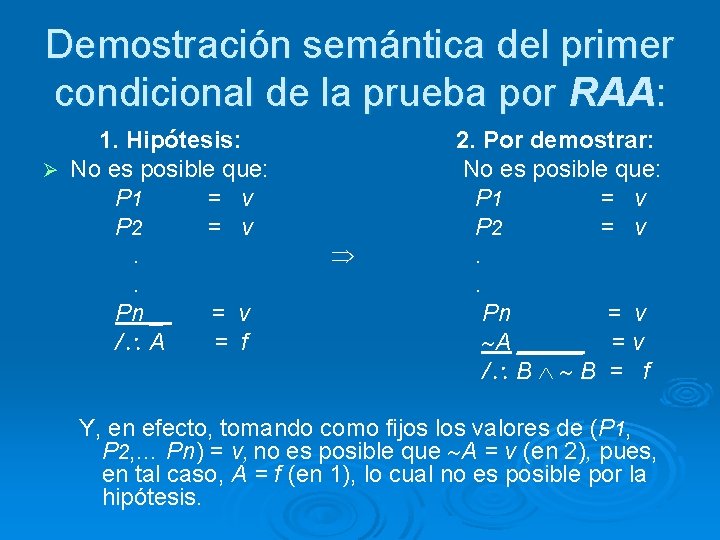
Demostración semántica del primer condicional de la PC: 1. Hipótesis: Ø No es posible que: P 1 = P 2 =. . Pn ___ = / A B = 2. Por demostrar: No es posible que: v P 1 = v v P 2 = v . . v Pn = v f A___ = v / B = f Y, en efecto, tomando como fijos los valores de (P 1, P 2, … Pn) = v, no es posible que A = v y B = f (en 2), pues, en tal caso, A B = f (en 1), lo cual no es posible por la hipótesis.

Demostración semántica del segundo condicional de la PC: 1. Hipótesis: 2. Por demostrar: Ø No es posible que: P 1 = v P 2 = v. . . . Pn = v Pn_____ = v A___ = v / A B = f / B = f Y, en efecto, tomando como fijos los valores de (P 1, P 2, … Pn) = v, no es posible que A B = f (en 2), pues, en tal caso, A = v y B = f (en 1), lo cual no es posible por la hipótesis.

DEMOSTRACIÓN SEMÁNTICA DE LA PRUEBA POR RAA Ø Si P 1, P 2, …, Pn son las fórmulas-premisa de un argumento cualquiera, A su fórmula-conclusión y B una subfórmula cualquiera de P 1, P 2, …, Pn o A, entonces Ø No es posible que: P 1 = v P 2 = v. . Pn _ = v / A = f No es posible que: P 1 = v P 2 = v. . Pn = v A_____ = v / B B = f

Demostración semántica del primer condicional de la prueba por RAA: 1. Hipótesis: Ø No es posible que: P 1 = v P 2 = v. . Pn _ = v / A = f 2. Por demostrar: No es posible que: P 1 = v P 2 = v. . Pn = v A _____ = v / B B = f Y, en efecto, tomando como fijos los valores de (P 1, P 2, … Pn) = v, no es posible que A = v (en 2), pues, en tal caso, A = f (en 1), lo cual no es posible por la hipótesis.

Demostración semántica del segundo condicional de la prueba por RAA: 1. Hipótesis: 2. Por demostrar: Ø No es posible que: P 1 = v P 2 = v. . . . Pn = v Pn__ = v A______ = v / A = f / B B = f Y, en efecto, tomando como fijos los valores de (P 1, P 2, … Pn) = v, no es posible que A = f (en 2), pues, en tal caso, A = v , lo cual no es posible por la hipótesis.

DEMOSTRACIÓN FORMAL DE LA PC Ø Si P 1, P 2, …, Pn son las fórmulas-premisa de un argumento cualquiera y A B su fórmula-conclusión, entonces: P 1 P 2. . Pn_______ / A B P 2. . Pn A___ / B

Demostración formal del primer condicional de la PC: Hipótesis: Por demostrar: P 1 P 2. . Pn_____ / A B P 1 P 2. . Pn A___ / B

Demostración: 1. 2. . . n. n+1. . . n+k+1. P 1 P 2 Pn A / B A B B 1, 2, …, n, Hip. n+1, n+k, MP

Demostración formal del segundo condicional de la PC: Hipótesis: P 1 P 2. . Pn A___ / B Por demostrar: P 1 P 2. . Pn____ / A B

Demostración: 1. P 1 2. P 2. n. Pn / A B. n+(n-1). P 1 P 2 Pn 1, 2, …n, Conj. . n+(n-1)+k. (P 1 P 2 Pn A) B Hip. , LEF n+(n-1)+k+1. (P 1 P 2 Pn) (A B) n+(n-1)+k, Exp. n+(n-1)+k+2. A B n+(n-1), n+(n-1)+k+1, MP

DEMOSTRACIÓN FORMAL DE LA PRUEBA POR RAA Ø Si P 1, P 2, …, Pn son las fórmulas-premisa de un argumento cualquiera, A su fórmula-conclusión y B una subfórmula cualquiera de P 1, P 2, …, Pn o A, entonces P 1 P 2. . Pn__ / A P 1 P 2. . Pn A______ / B B

Demostración formal del primer condicional de la prueba por RAA: Hipótesis: P 1 P 2. . Pn__ / A Por demostrar: P 1 P 2. . Pn A____ / B B

Demostración 1. 2. . . n. P 1 P 2 Pn n+1. A. . n+k. A n+k+1. A v (B B) N+K+2 B B / B B 1, 2, …, n, Hip. n+k Ad n+1, n+k+1, SD

Demostración formal del segundo condicional de la prueba por RAA: Hipótesis: P 1 P 2. . Pn A_____ / B B Por demostrar: P 1 P 2. . Pn__ / A

Demostración: 1. 2. . . n+k. N+k+1. n+k+2. n+k+3. n+k+4. P 1 P 2 Pn A (B B) A v (B B) A v (B B ) (A ( v B) (A v B) A / A Hip. , PC n+k, IM n+k+1, DN n+k+2, Dist n+k+3, LEF

UTILIDAD DE LOS MÉTODOS DE DEMOSTRACIÓN DE LA PC Y LA RAA En general, la utilidad de ambos métodos radica en que facilitan las deducciones pues, debido a la premisa extra que permiten añadir, aumentan las posibilidades deductivas respecto del conjunto original de premisas. Ø En particular, la PC se aplica con provecho a la demostración de fórmulas cuya conectiva principal sea ‘ ’, ‘≡’ o ‘v’; mientras que la RAA se puede aplicar con provecho a cualquier tipo de fórmula. Ø Usando cualquiera de ambos métodos pueden deducirse conclusiones intermedias que coadyuven, luego, a deducir la conclusión final de argumentos; también pueden combinarse ambos en una misma deducción. En todos estos casos deben introducirse hipótesis con alcances limitados en las demostraciones, cuidándose de cerrarlos adecuadamente a fin de evitar falacias en las deducciones. Ø

UTILIDAD DE LOS MÉTODOS DE DEMOSTRACIÓN DE LA PC Y LA RAA El sistema de reglas de deducción natural para la LP modificado, mencionado al principio de esta charla, cuenta con una LEF para introducir tautologías, por lo que es completo: ‘A [(A B) (A B)]’. Mediante esta regla puede demostrarse que una tautología se deduce de cualquier fórmula. Ø Los métodos de la PC y la RAA también permiten introducir tautologías en las demostraciones. Se diferencian de LEF en que son más manejables, debido a lo ya mencionado, y más potentes, pues permiten demostrar que una tautología se deduce del conjunto vacío de fórmulas. Ø En sistemas de deducción directa incompletos en los que no se pueden demostrar tautologías (como el de Copi en Lógica simbólica) estos métodos permiten, pues, completarlos (tal como lo hace Copi con su sistema mencionado). Ø

GRACIAS POR SUS COMENTARIOS Y CRÍTICAS
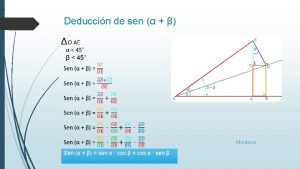
 Sen de 45
Sen de 45 Serie cronologica en excel
Serie cronologica en excel Clculo
Clculo Hojas de clculo
Hojas de clculo Esquema de una hoja
Esquema de una hoja Hojas de clculo
Hojas de clculo Tablas mentales
Tablas mentales Natural hazards vs natural disasters
Natural hazards vs natural disasters Natural capital
Natural capital Antigenos virales
Antigenos virales Plano europeo y americano
Plano europeo y americano Sistema 1 sistema 2
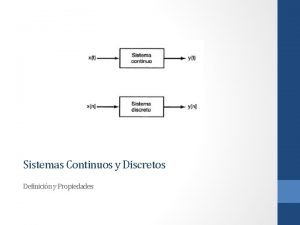
Sistema 1 sistema 2 Sistema continuo y sistema discreto
Sistema continuo y sistema discreto Sistema semashko o sistema centralizado
Sistema semashko o sistema centralizado Paisagem natural e paisagem modificada
Paisagem natural e paisagem modificada Paisaje natural y cultural para niños de primaria
Paisaje natural y cultural para niños de primaria Sistemas de informacion para ejecutivos
Sistemas de informacion para ejecutivos Sistemas de información para ejecutivos
Sistemas de información para ejecutivos Pensamiento aleatorio ejercicios
Pensamiento aleatorio ejercicios Relieve periférico
Relieve periférico Adivinanzas sistema solar
Adivinanzas sistema solar Sistema venda direta
Sistema venda direta Escaleno musculo
Escaleno musculo Moneycar login
Moneycar login Objetivo del sistema de ahorro para el retiro
Objetivo del sistema de ahorro para el retiro Glandula que produce insulina
Glandula que produce insulina Sistema web para gerenciamento
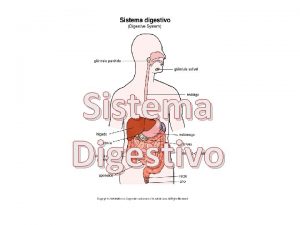
Sistema web para gerenciamento Sistema digestivo
Sistema digestivo Objetivos verticales
Objetivos verticales Imagen del sistema respiratorio con todas sus partes
Imagen del sistema respiratorio con todas sus partes Termorreceptores
Termorreceptores Mapa conceptual del sistema muscular
Mapa conceptual del sistema muscular Que es la degradacion en el sistema digestivo
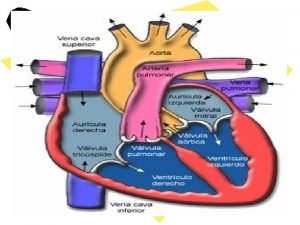
Que es la degradacion en el sistema digestivo Recorrido de la sangre dentro del corazón
Recorrido de la sangre dentro del corazón Roscas de potencia
Roscas de potencia Sistemas operativos y sus funciones
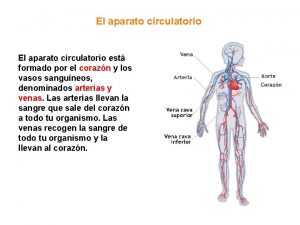
Sistemas operativos y sus funciones Sistema circulatorio y sus partes para niños
Sistema circulatorio y sus partes para niños Sistema nacional para la calidad
Sistema nacional para la calidad Carnet de cientifico para niños
Carnet de cientifico para niños