Tratamento de rudos em imagens e aplicaes da
























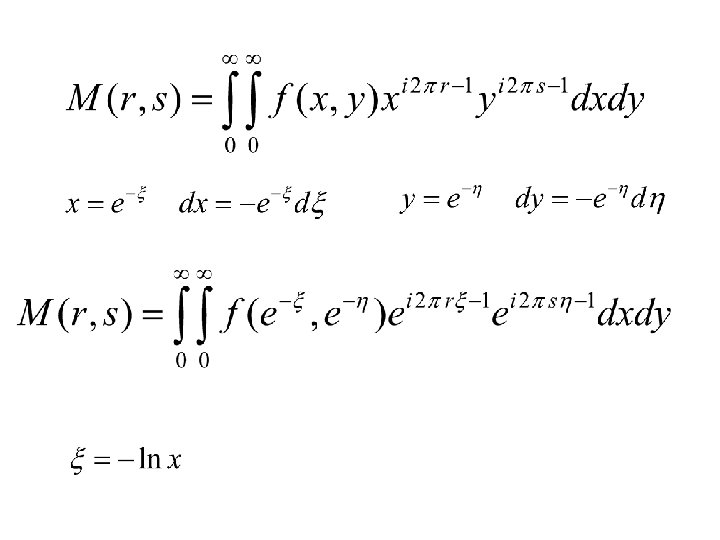










- Slides: 73

Tratamento de ruídos em imagens e aplicações da transformada de Fourier

Redução de ruídos • Dada uma imagem I com um ruído n, reduza n o máximo que puder (preferencialmente elimine n completamente) sem alterar significativamente I. 20 d. B significam

Dois tipos básicos de ruídos • Ruído Gaussiano branco : processo estocástico de média zero, independente do tempo e dos espaço. é o mesmo processo estocástico que não varia no tempo. é uma variável aleatória com a distribuição:

Dois tipos básicos de ruídos • Ruído impulsivo: causado por erro de transmissão, CCDs defeituosos, etc. . . Também chamado de pico e de sal e pimenta. são v. a. uniformemente distribuídas imin, imax, e l são parâmetos de controle da quantidade de ruídos.

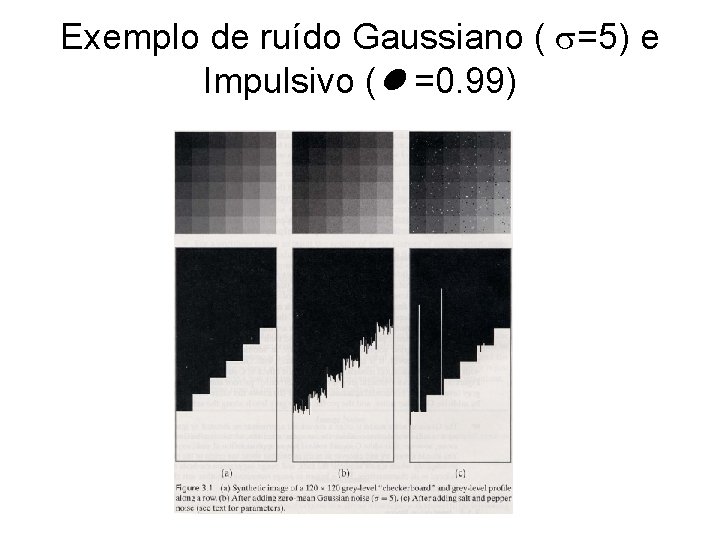
Exemplo de ruído Gaussiano ( =5) e Impulsivo ( =0. 99)


Imagem com ruído impulsivo Uso da mediana 223 204 204 204 223 171 120 120 18 120 50 120 120 120 171 120 120 116 120 120 171 138 120 120 120 50 120 97 120 120 171 120 120 120 187 120 242 172 120 120 120 171 120 120 120 179 120 120 167 120 171 120 120 120 235 120 120 120 171 120 120 120 235 120 76 175 120 171 120 120 120 171 120 120 123 120 214 120 114 171 120 120 120 143 171 120 120 232 120 198 120 120 120 171 203 171 171 205 171 171 203 Iij = mediana Ωij

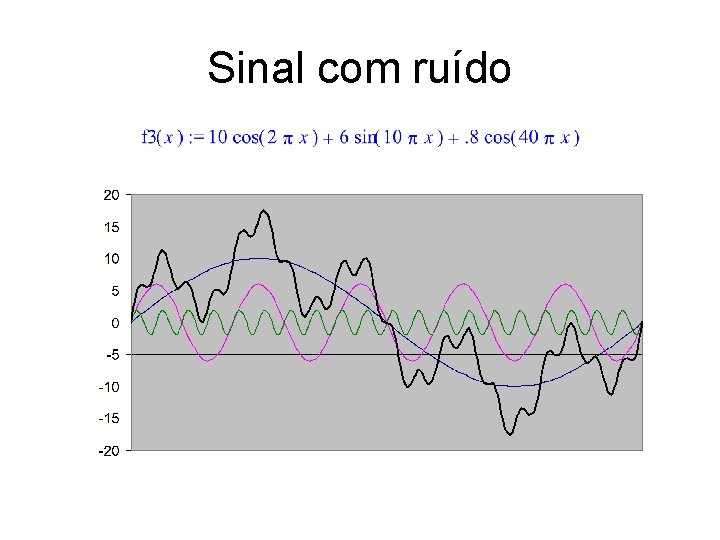
Sinal com ruído

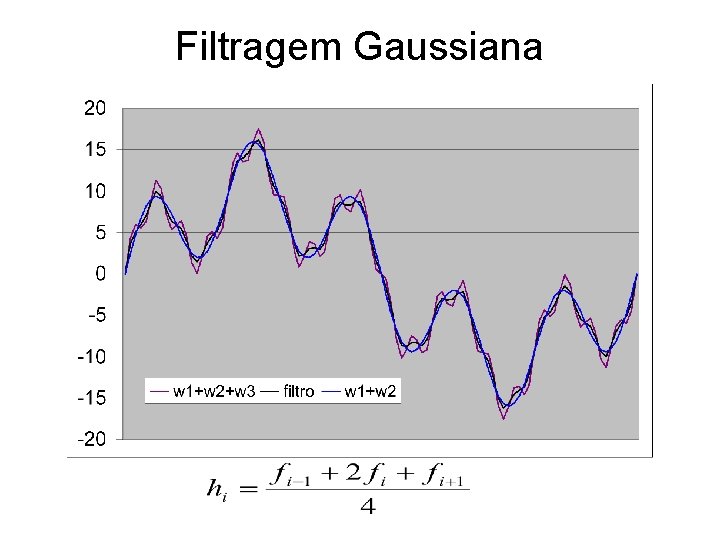
Filtragem Gaussiana

Mascara ou Filtro ou:

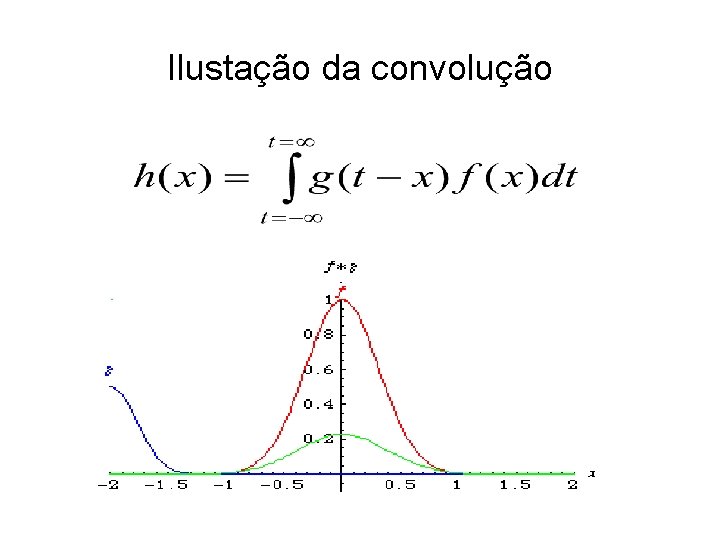
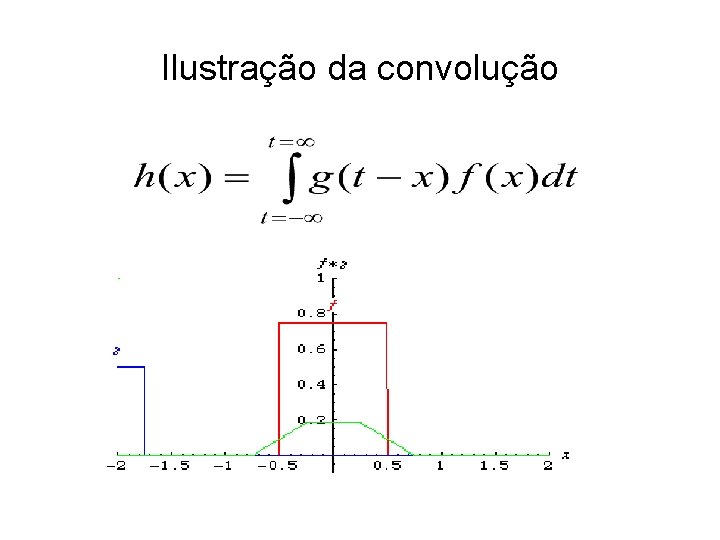
Convolução

Ilustação da convolução

Ilustração da convolução

Discretização da Gaussiana 1 D 0. 3 0. 2 0. 1 -4 -3 -2 -1 0 1 2 3 4

Discretização da Gaussiana 2 D

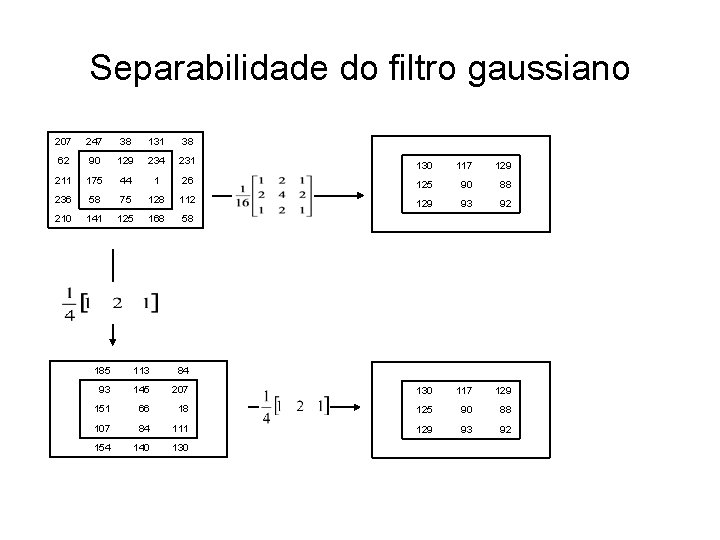
Separabilidade do filtro gaussiano 207 247 38 131 38 62 90 129 234 231 130 117 129 211 175 44 1 26 125 90 88 236 58 75 128 112 129 93 92 210 141 125 168 58 185 113 84 93 145 207 130 117 129 151 66 18 125 90 88 107 84 111 129 93 92 154 140 130

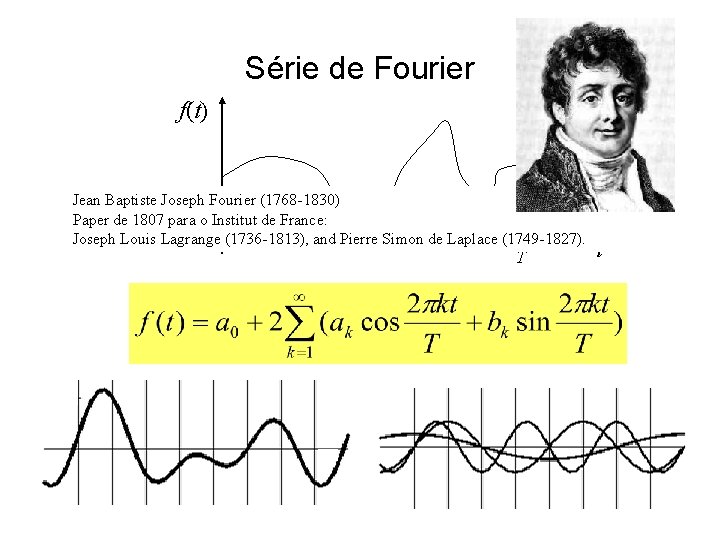
Série de Fourier f(t) Jean Baptiste Joseph Fourier (1768 -1830) Paper de 1807 para o Institut de France: Joseph Louis Lagrange 0 (1736 -1813), and Pierre Simon de Laplace (1749 -1827). T t

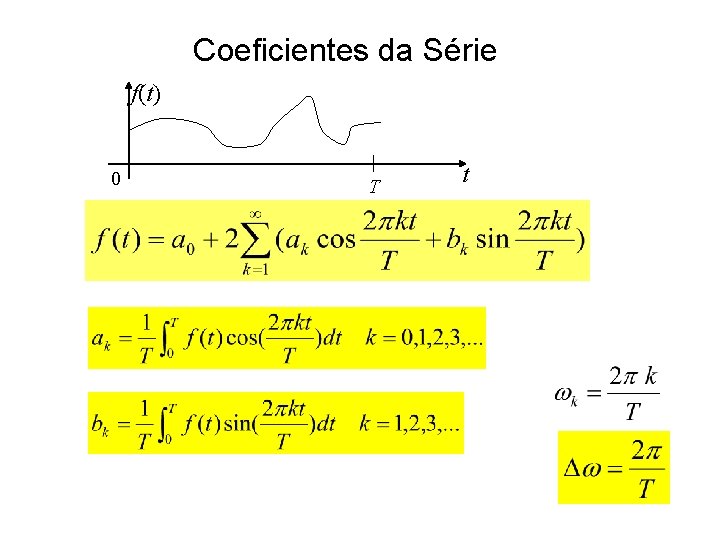
Coeficientes da Série f(t) 0 T t

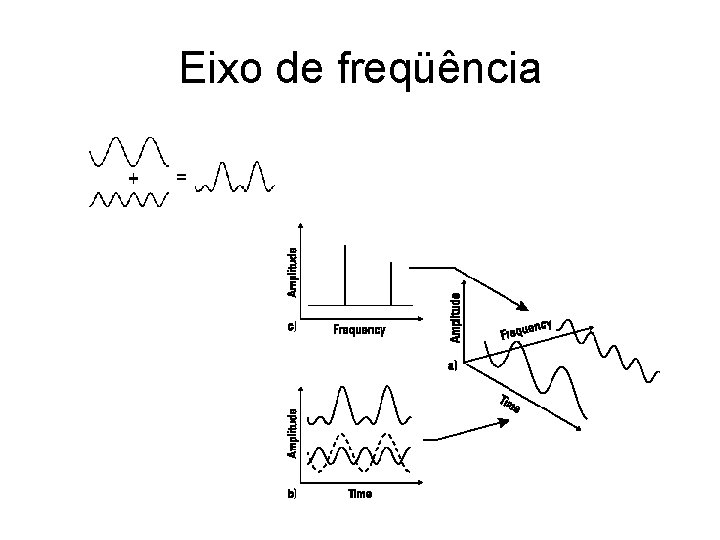
Eixo de freqüência

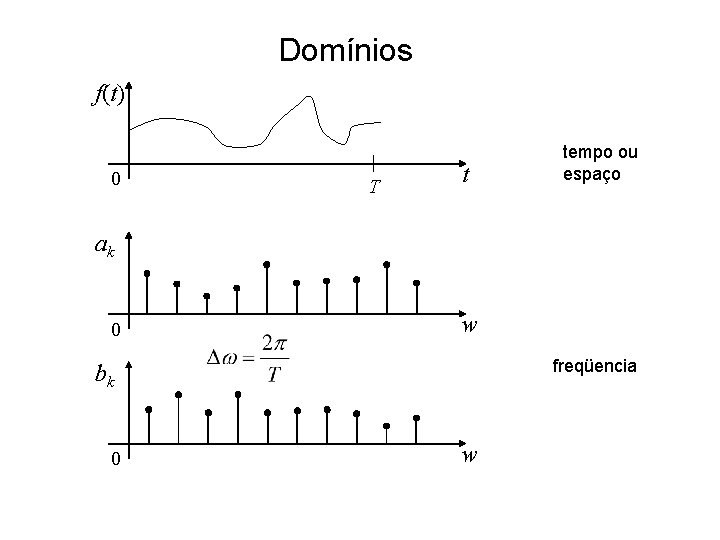
Domínios f(t) 0 T t tempo ou espaço ak 0 w freqüencia bk 0 w

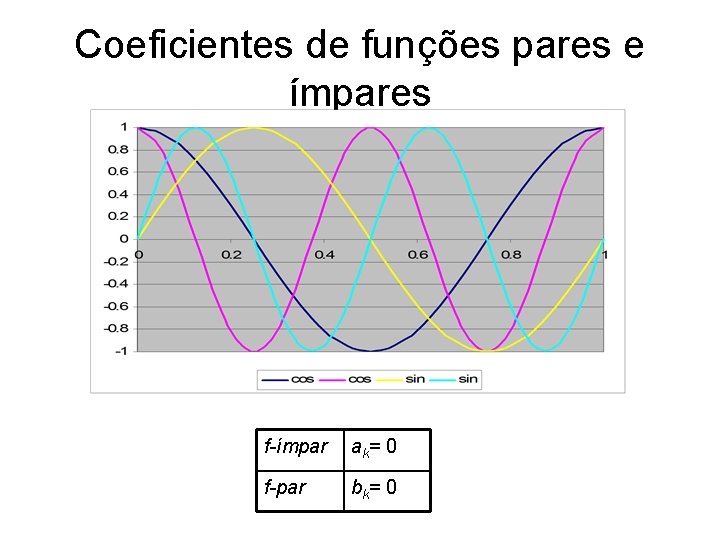
Coeficientes de funções pares e ímpares f-ímpar ak = 0 f-par bk = 0

Série de Fourier com números complexos

Escrevendo em complexos

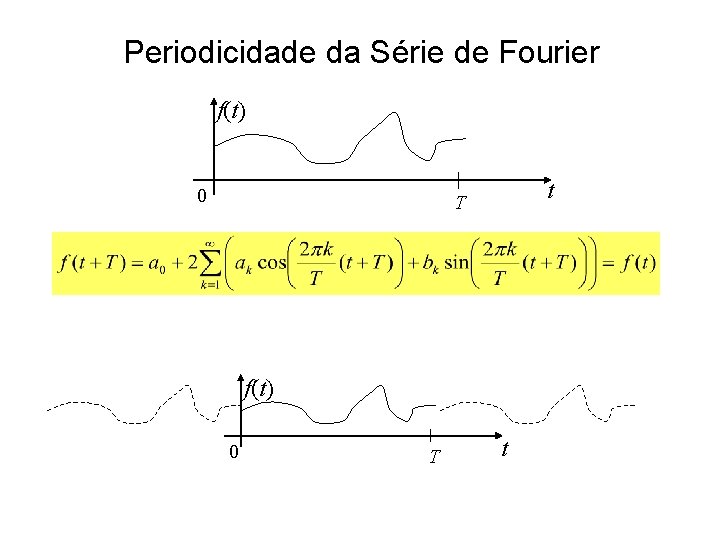
Periodicidade da Série de Fourier f(t) 0 t T f(t) 0 T t

Transformada de Fourier

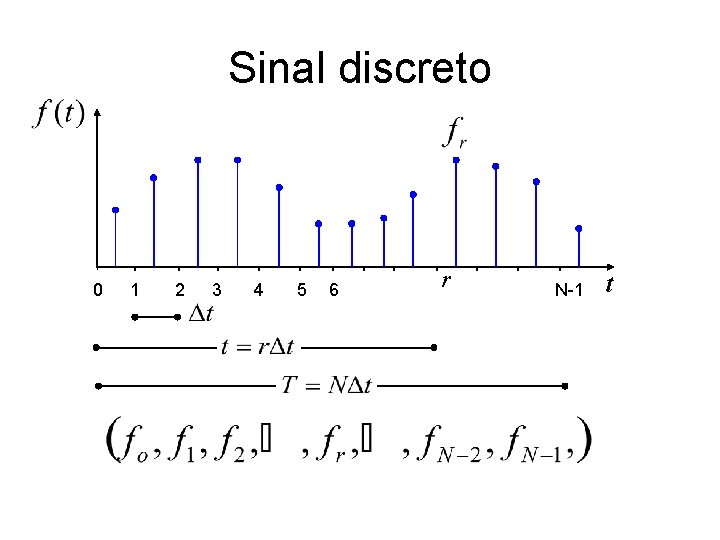
Sinal discreto 0 1 2 3 4 5 6 r N-1 t

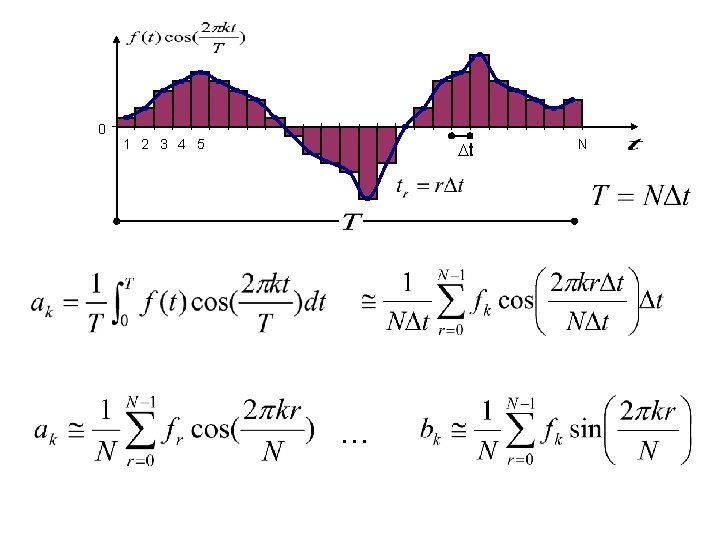
0 1 2 3 4 5 t . . . N

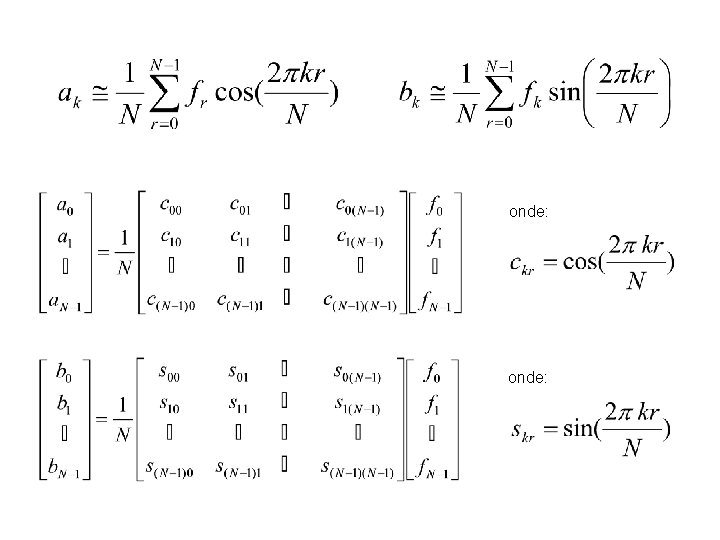
onde:

onde:

Transformada de Fourier

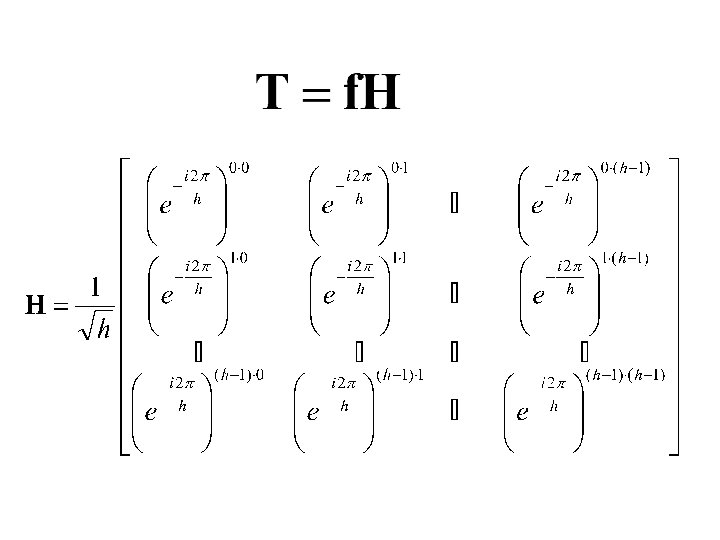
Transformada de Fourier (discreta e normalizada)

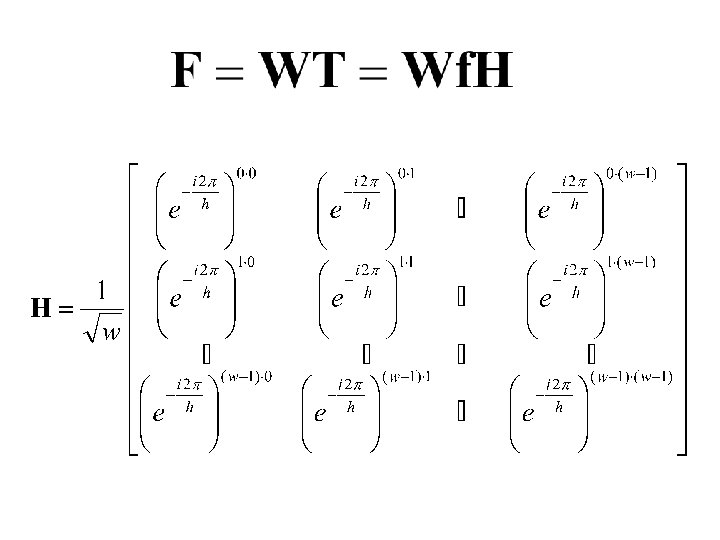
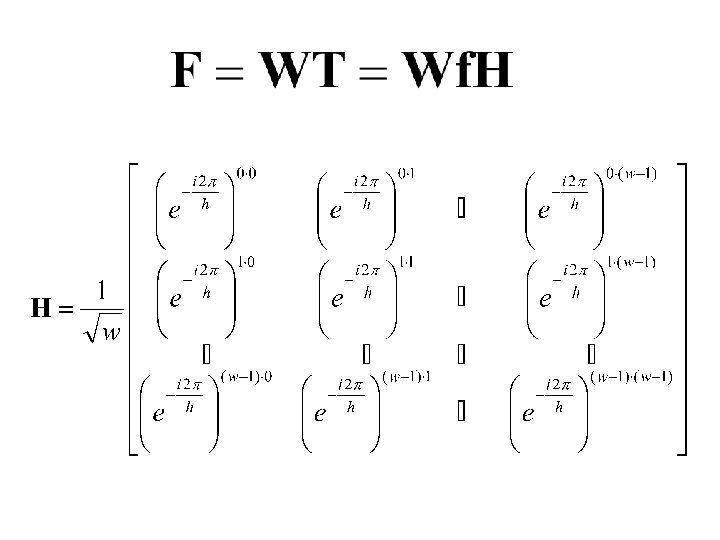
Transformada normalizada de Fourier: separação

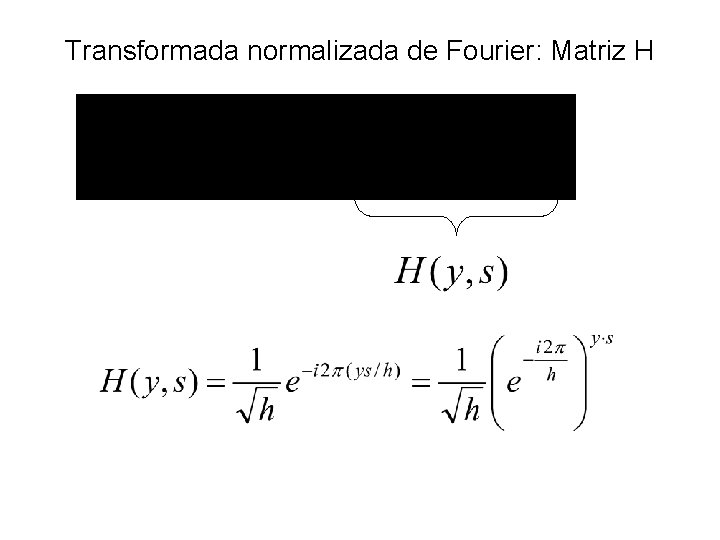
Transformada normalizada de Fourier: Matriz H





Problemas com a Transformada de Fourier

Transformada de Mellin

Transformada de Mellin

Transformada de Mellin

Transformada de Mellin


Transformada de Mellin
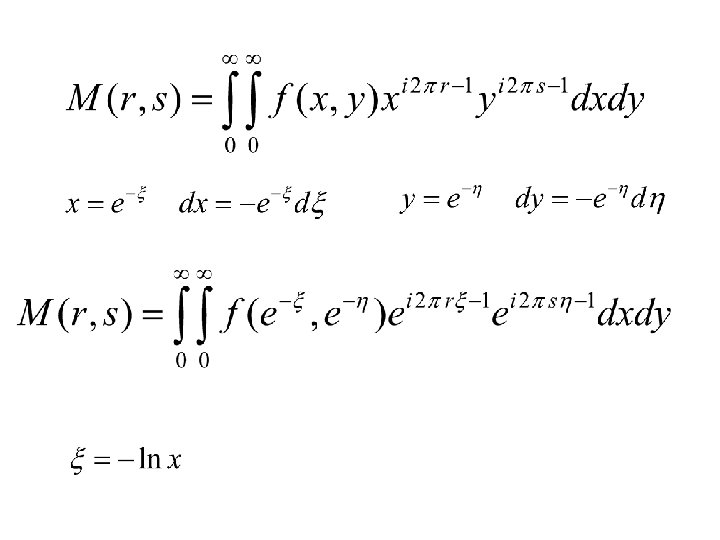

Resultados da Transformada de Fourier

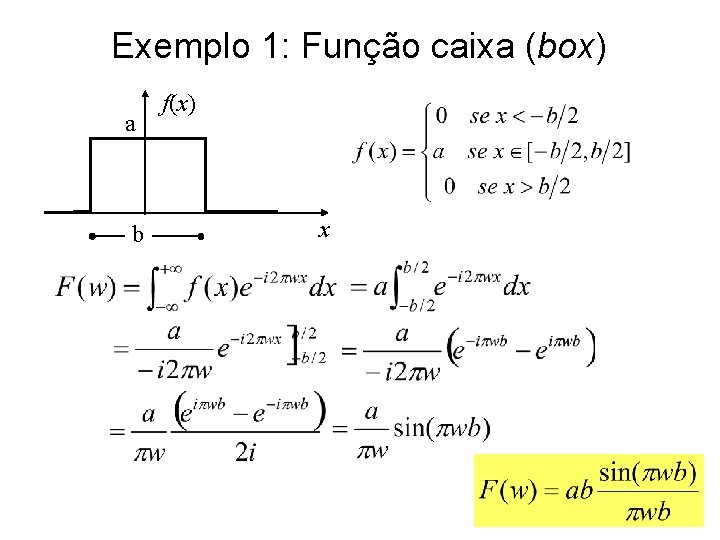
Exemplo 1: Função caixa (box) a b f(x) x

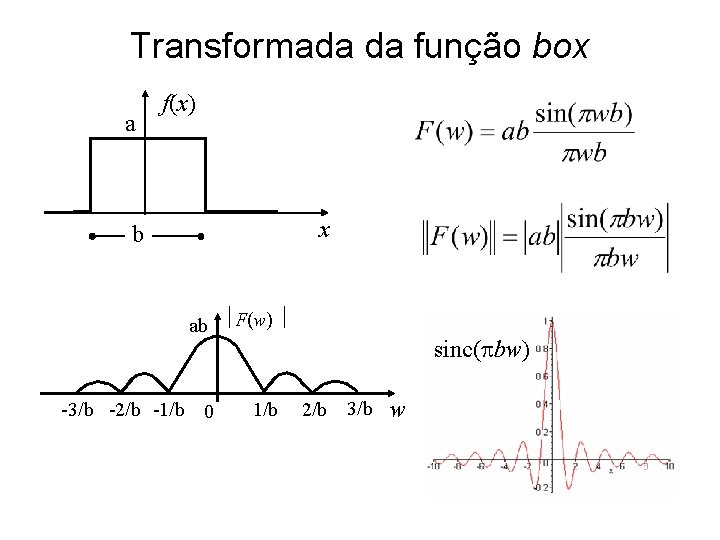
Transformada da função box a f(x) x b ab F(w) -3/b -2/b -1/b 0 1/b sinc( bw) 2/b 3/b w

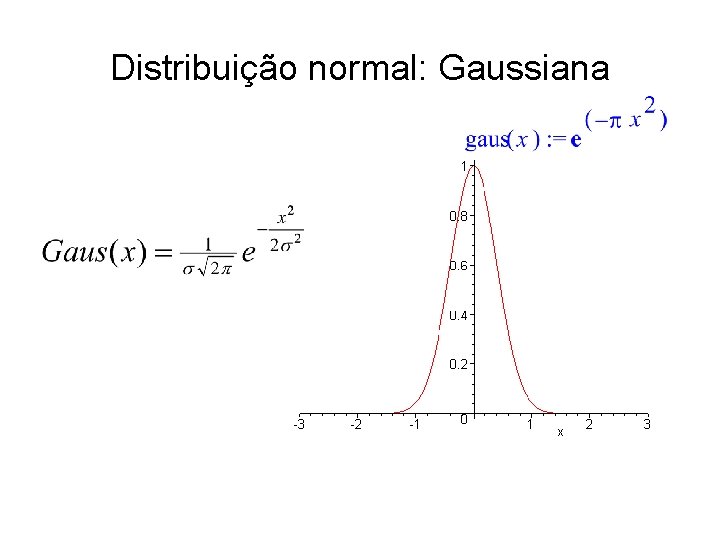
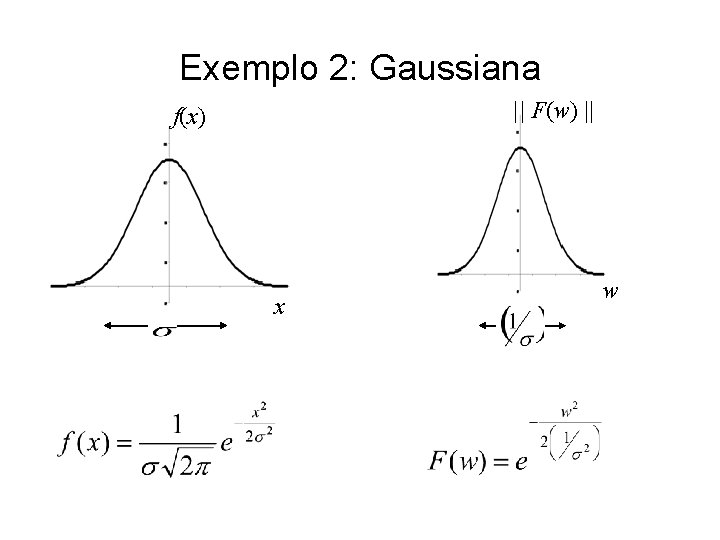
Distribuição normal: Gaussiana

Exemplo 2: Gaussiana || F(w) || f(x) x w

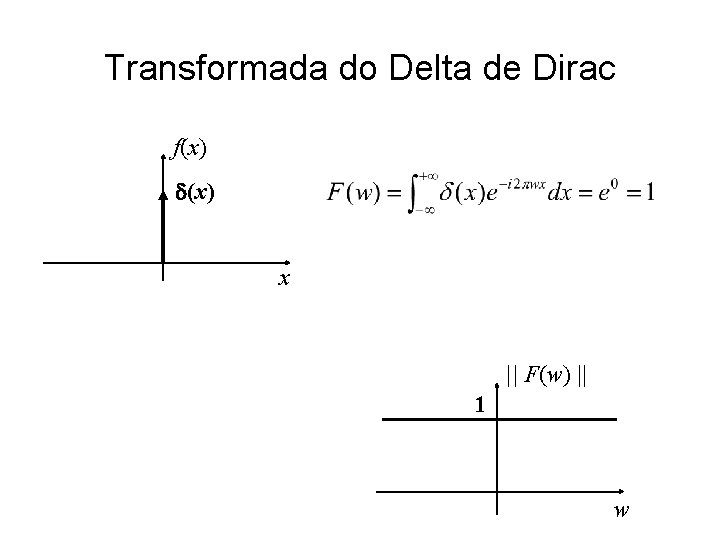
Transformada do Delta de Dirac f(x) x || F(w) || 1 w

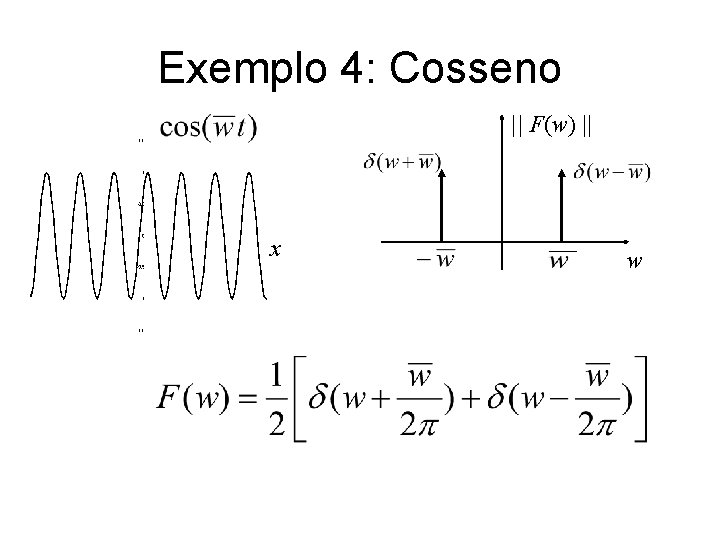
Exemplo 4: Cosseno || F(w) || x w

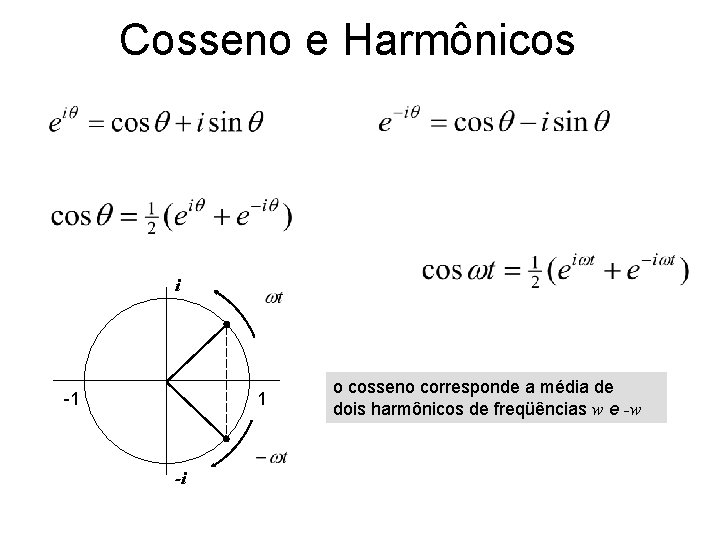
Cosseno e Harmônicos i -1 1 -i o cosseno corresponde a média de dois harmônicos de freqüências w e -w

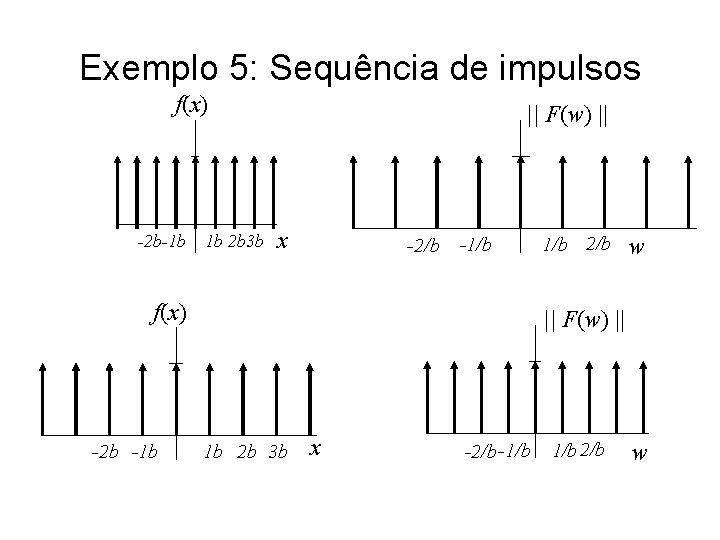
Exemplo 5: Sequência de impulsos f(x) -2 b-1 b 1 b 2 b 3 b || F(w) || x -2/b -1/b f(x) -2 b -1 b 1/b 2/b w || F(w) || 1 b 2 b 3 b x -2/b -1/b 2/b w

Pares importantes

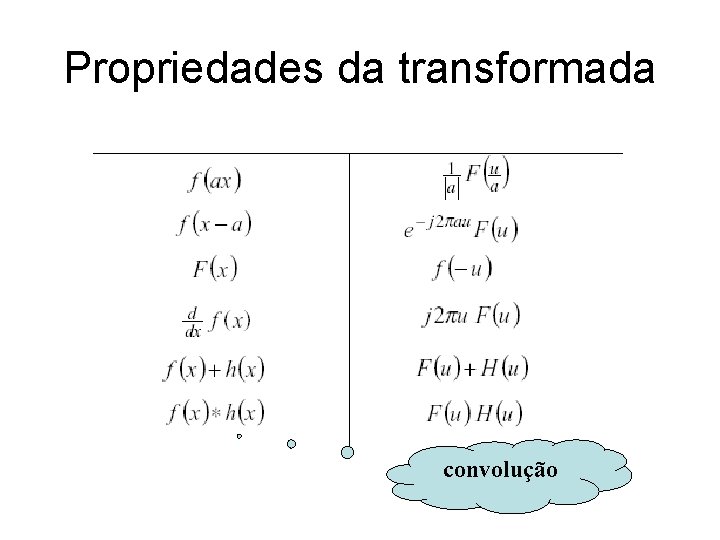
Propriedades da transformada convolução

Filtragem nos domínios espacial e de freqüência ou: • Filtragem no domínio espacial pode ser obtida pela convolução • Filtragem no domínio da frequencia pode ser obtida por uma transformada, seguida de um produto e de uma transformada inversa.

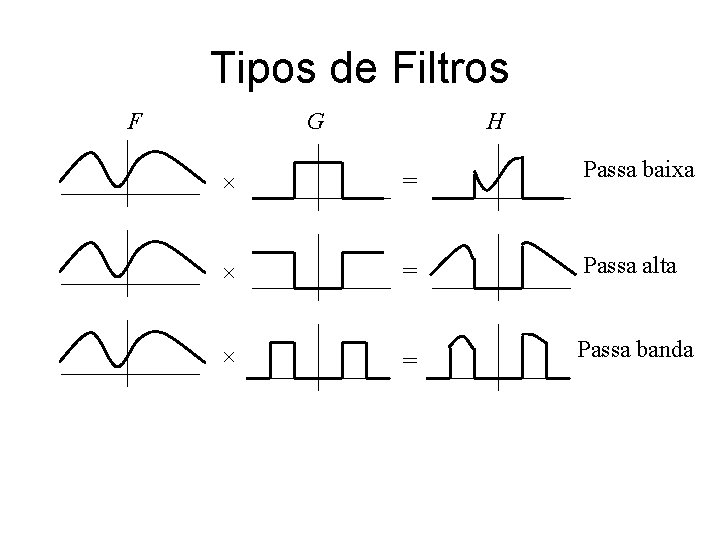
Tipos de Filtros F G H = Passa baixa = Passa alta = Passa banda

Imagem filtrada com um filtro passa baixa

Imagem filtrada com um filtro passa alta

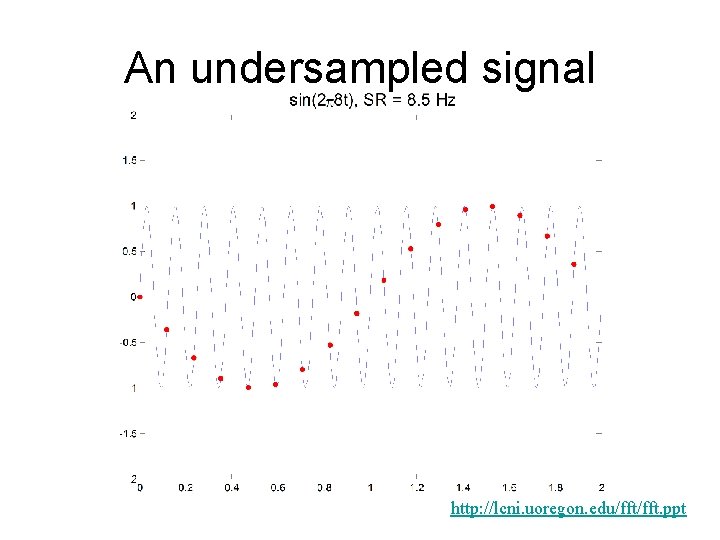
An undersampled signal http: //lcni. uoregon. edu/fft. ppt

Amostragem e Reconstrução Observando os domínio do espaço e das freqüências

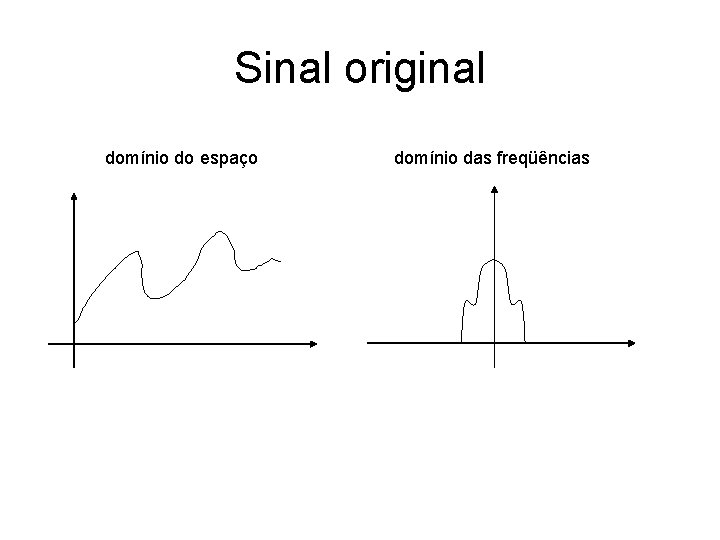
Sinal original domínio do espaço domínio das freqüências

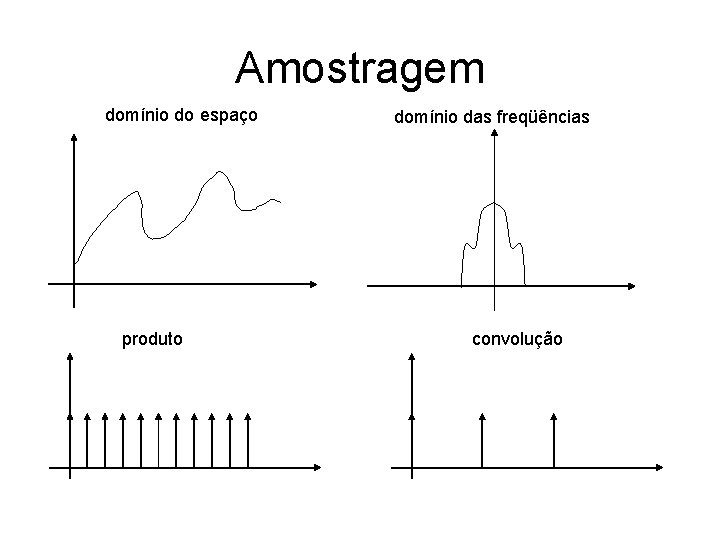
Amostragem domínio do espaço produto domínio das freqüências convolução

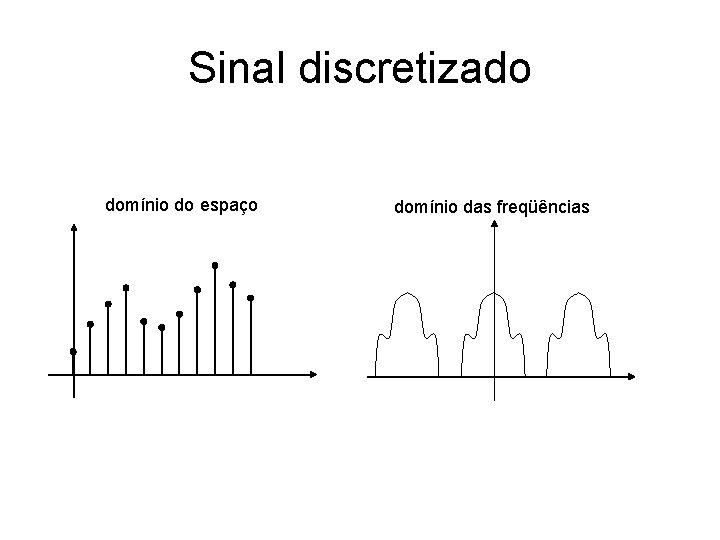
Sinal discretizado domínio do espaço domínio das freqüências

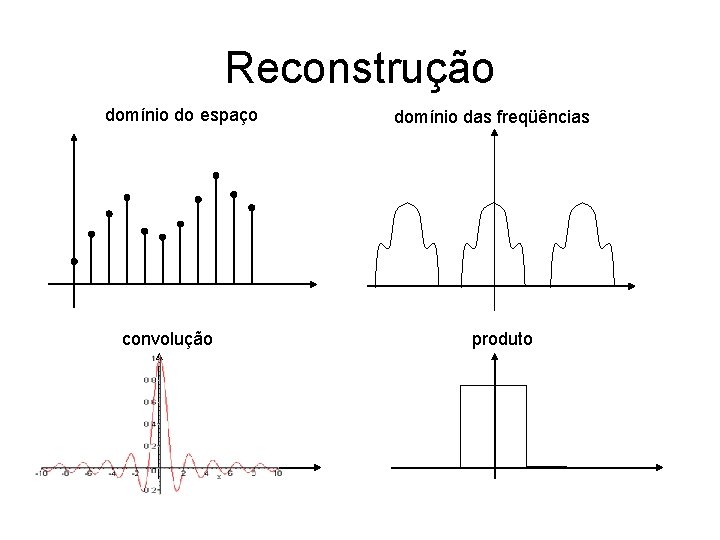
Reconstrução domínio do espaço convolução domínio das freqüências produto

Retorno ao sinal original domínio do espaço domínio das freqüências

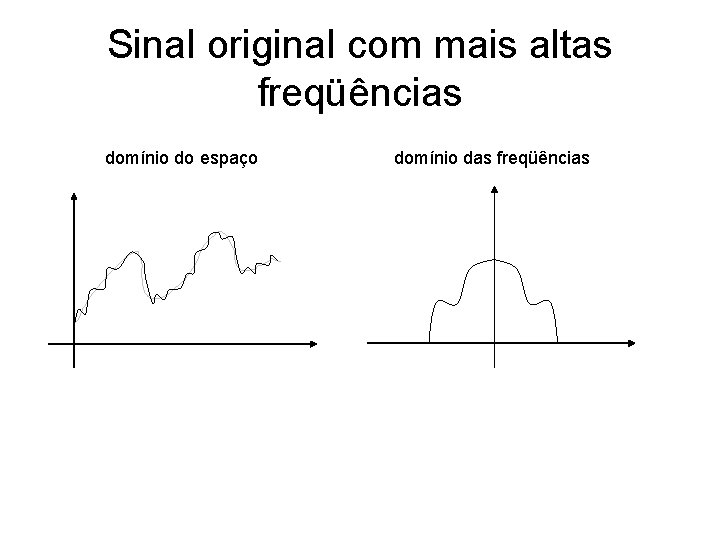
Sinal original com mais altas freqüências domínio do espaço domínio das freqüências

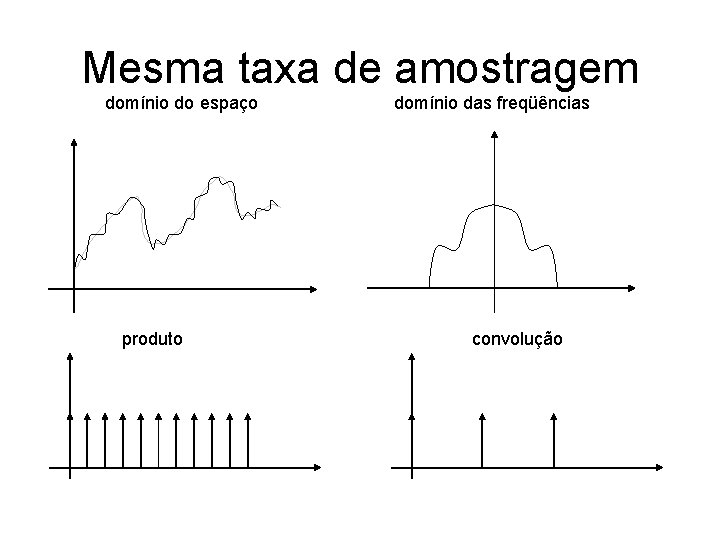
Mesma taxa de amostragem domínio do espaço produto domínio das freqüências convolução

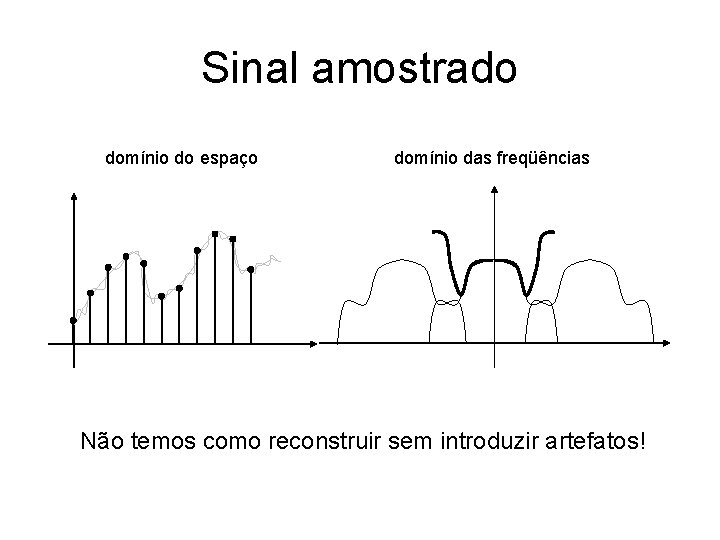
Sinal amostrado domínio do espaço domínio das freqüências Não temos como reconstruir sem introduzir artefatos!

Teorema de Nyquist Para que um sinal de banda limitada (i. e. aqueles cuja a transformada resultam em zero para freqüências f > B) seja reconstruido plenamente ele precisa ser amostrado numa freqüência f >= 2 B. Um sinal amostrado na freqüência (f=2 B) é dito amostrado por Nyquist e f=2 B é a freqüência de Nyquist. Não há perda de informação nos sinais amostrados na freqüência de Nyquist, e não adicionamos nenhuma informação se amostrarmos numa freqüência maior.

Aliasing • Esta mistura de espectros é chamada de aliasing. • Existem duas maneiras de lidarmos com aliasing. – Passar um filtro passa-baixa no sinal. – Aumentar a freqüência de amostragem.

Alias Texture errors