Transition of Component States Normal state continues Component

Transition of Component States Normal state continues Component fails N F Component is repaired Failed state continues

The Repair-to-Failure Process

Definition of Reliability • The reliability of an item is the probability that it will adequately perform its specified purpose for a specified period of time under specified environmental conditions.

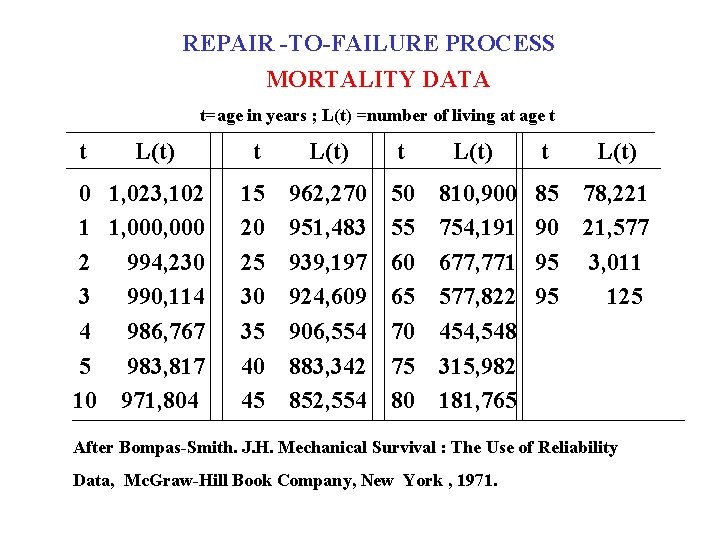
REPAIR -TO-FAILURE PROCESS MORTALITY DATA t=age in years ; L(t) =number of living at age t t L(t) 0 1, 023, 102 1 1, 000 2 994, 230 3 990, 114 4 986, 767 5 983, 817 10 971, 804 t L(t) 15 20 25 30 35 40 45 962, 270 951, 483 939, 197 924, 609 906, 554 883, 342 852, 554 50 55 60 65 70 75 80 810, 900 754, 191 677, 771 577, 822 454, 548 315, 982 181, 765 85 90 95 95 78, 221 21, 577 3, 011 125 After Bompas-Smith. J. H. Mechanical Survival : The Use of Reliability Data, Mc. Graw-Hill Book Company, New York , 1971.

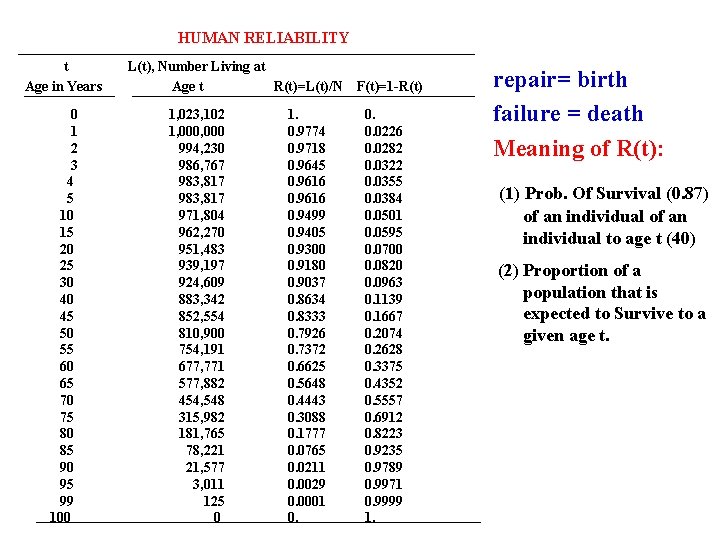
HUMAN RELIABILITY t Age in Years 0 1 2 3 4 5 10 15 20 25 30 40 45 50 55 60 65 70 75 80 85 90 95 99 100 L(t), Number Living at Age t R(t)=L(t)/N 1, 023, 102 1, 000 994, 230 986, 767 983, 817 971, 804 962, 270 951, 483 939, 197 924, 609 883, 342 852, 554 810, 900 754, 191 677, 771 577, 882 454, 548 315, 982 181, 765 78, 221 21, 577 3, 011 125 0 1. 0. 9774 0. 9718 0. 9645 0. 9616 0. 9499 0. 9405 0. 9300 0. 9180 0. 9037 0. 8634 0. 8333 0. 7926 0. 7372 0. 6625 0. 5648 0. 4443 0. 3088 0. 1777 0. 0765 0. 0211 0. 0029 0. 0001 0. F(t)=1 -R(t) 0. 0. 0226 0. 0282 0. 0322 0. 0355 0. 0384 0. 0501 0. 0595 0. 0700 0. 0820 0. 0963 0. 1139 0. 1667 0. 2074 0. 2628 0. 3375 0. 4352 0. 5557 0. 6912 0. 8223 0. 9235 0. 9789 0. 9971 0. 9999 1. repair= birth failure = death Meaning of R(t): (1) Prob. Of Survival (0. 87) of an individual to age t (40) (2) Proportion of a population that is expected to Survive to a given age t.

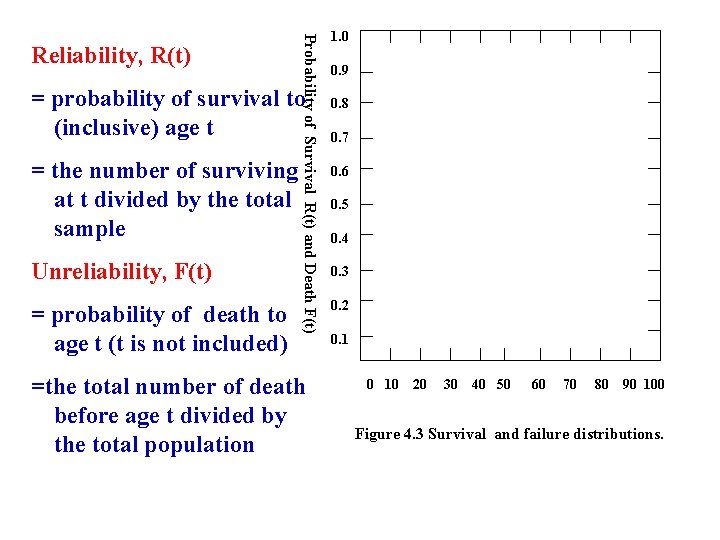
Probability of Survival R(t) and Death F(t) Reliability, R(t) = probability of survival to (inclusive) age t = the number of surviving at t divided by the total sample Unreliability, F(t) = probability of death to age t (t is not included) =the total number of death before age t divided by the total population 1. 0 0. 9 0. 8 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0 10 20 30 40 50 60 70 80 90 100 Figure 4. 3 Survival and failure distributions.

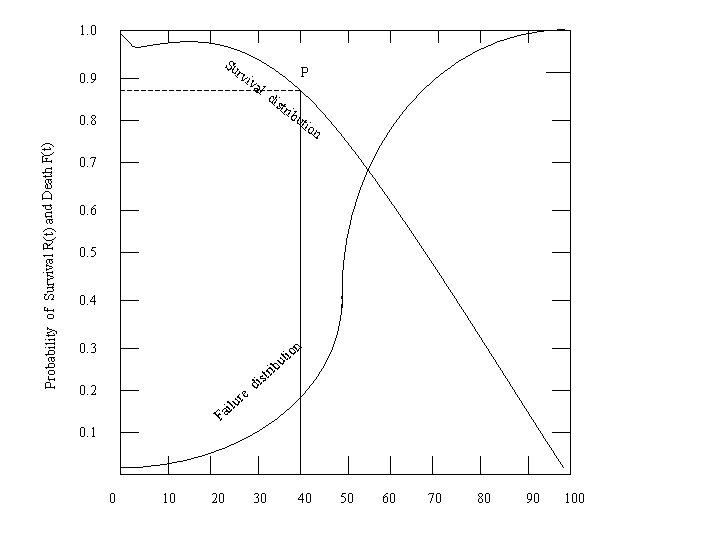
1. 0 Su rv 0. 9 0. 8 Probability of Survival R(t) and Death F(t) P iva ld ist rib uti on 0. 7 0. 6 0. 5 0. 4 0. 3 io ut 0. 2 e ur l i Fa n ib si tr d 0. 1 0 10 20 30 40 50 60 70 80 90 100

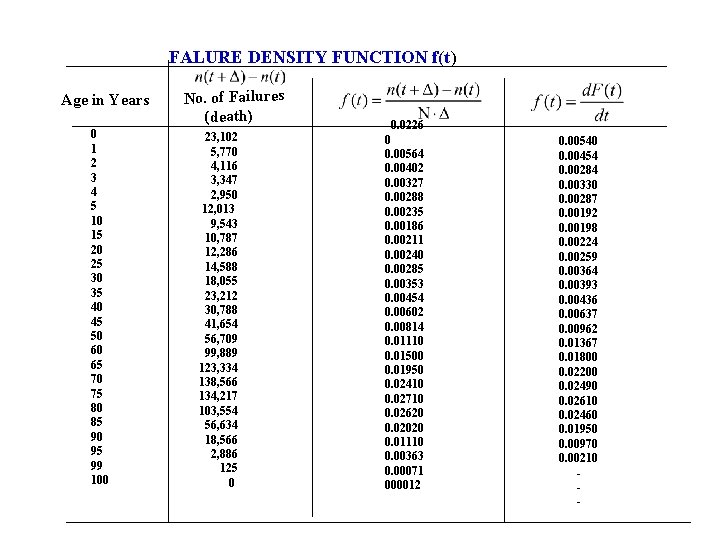
FALURE DENSITY FUNCTION f(t) Age in Years 0 1 2 3 4 5 10 15 20 25 30 35 40 45 50 60 65 70 75 80 85 90 95 99 100 No. of Failures (death) 23, 102 5, 770 4, 116 3, 347 2, 950 12, 013 9, 543 10, 787 12, 286 14, 588 18, 055 23, 212 30, 788 41, 654 56, 709 99, 889 123, 334 138, 566 134, 217 103, 554 56, 634 18, 566 2, 886 125 0 0. 0226 0 0. 00564 0. 00402 0. 00327 0. 00288 0. 00235 0. 00186 0. 00211 0. 00240 0. 00285 0. 00353 0. 00454 0. 00602 0. 00814 0. 01110 0. 01500 0. 01950 0. 02410 0. 02710 0. 02620 0. 02020 0. 01110 0. 00363 0. 00071 000012 0. 00540 0. 00454 0. 00284 0. 00330 0. 00287 0. 00192 0. 00198 0. 00224 0. 00259 0. 00364 0. 00393 0. 00436 0. 00637 0. 00962 0. 01367 0. 01800 0. 02200 0. 02490 0. 02610 0. 02460 0. 01950 0. 00970 0. 00210 -

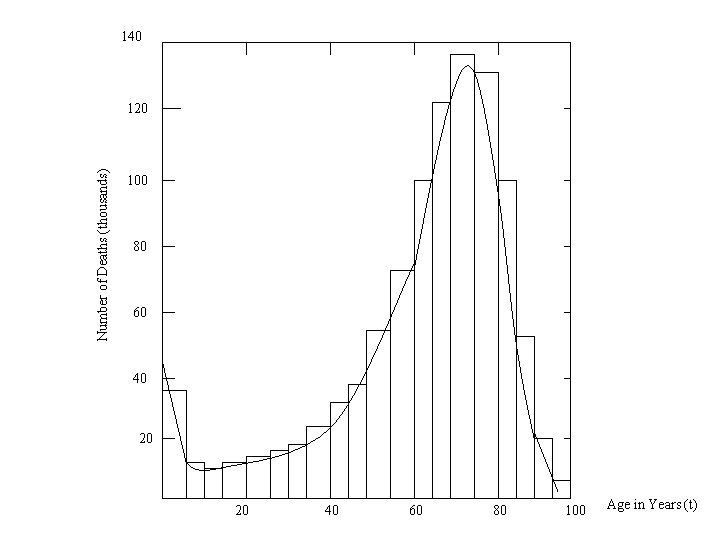
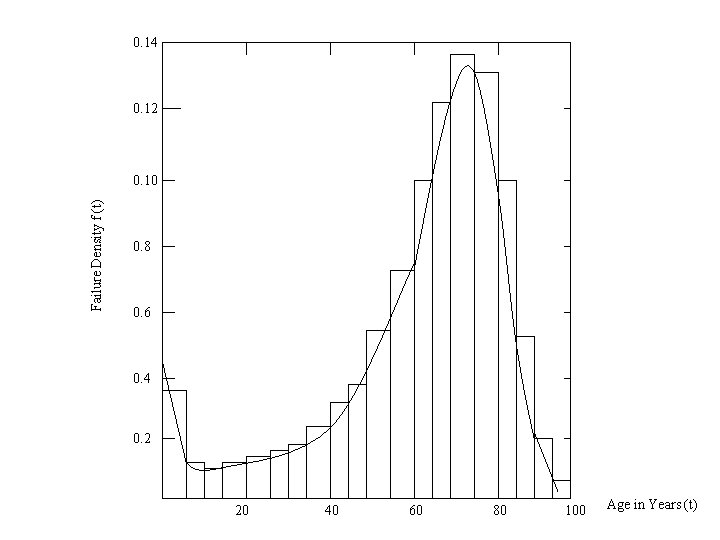
0. 14 120 0. 12 Failure Density f(t) Numbre of Deaths (thousands) 140 100 80 60 40 0. 10 0. 8 0. 6 0. 4 20 0. 2 0 20 40 60 Age in Years (t) 80 Figure 4. 4 Histogram and smooth curve 100 0. 0 0 20 40 60 80 100

140 Number of Deaths (thousands) 120 100 80 60 40 20 20 40 60 80 100 Age in Years (t)

0. 14 0. 12 Failure Density f (t) 0. 10 0. 8 0. 6 0. 4 0. 2 20 40 60 80 100 Age in Years (t)

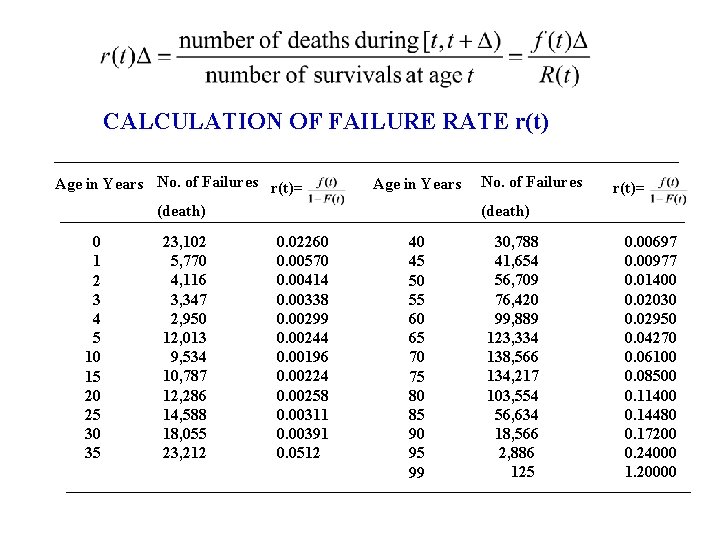
CALCULATION OF FAILURE RATE r(t) Age in Years No. of Failures r(t)= (death) 0 1 2 3 4 5 10 15 20 25 30 35 23, 102 5, 770 4, 116 3, 347 2, 950 12, 013 9, 534 10, 787 12, 286 14, 588 18, 055 23, 212 0. 02260 0. 00570 0. 00414 0. 00338 0. 00299 0. 00244 0. 00196 0. 00224 0. 00258 0. 00311 0. 00391 0. 0512 Age in Years No. of Failures r(t)= (death) 40 45 50 55 60 65 70 75 80 85 90 95 99 30, 788 41, 654 56, 709 76, 420 99, 889 123, 334 138, 566 134, 217 103, 554 56, 634 18, 566 2, 886 125 0. 00697 0. 00977 0. 01400 0. 02030 0. 02950 0. 04270 0. 06100 0. 08500 0. 11400 0. 14480 0. 17200 0. 24000 1. 20000

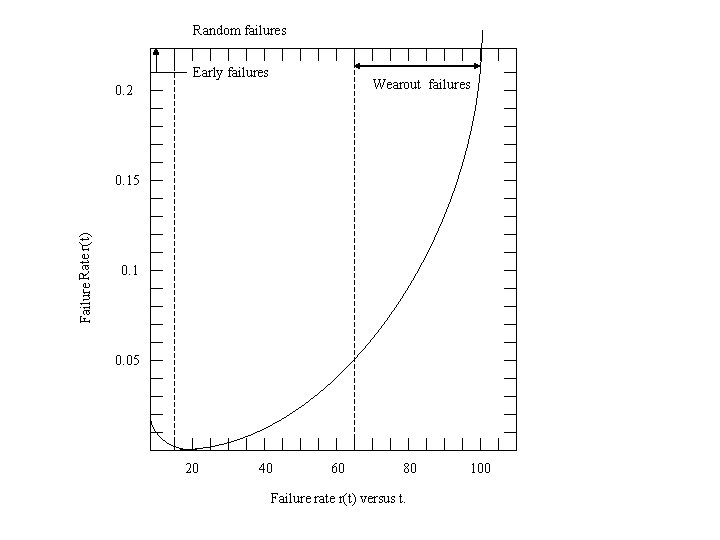
Random failures 0. 2 Wearout failures Failure rate f (t) 0. 15 0. 1 0. 05 0 20 40 60 80 t, years Figure 4. 6 Failure rate r (t) versus t. 100 Bathtub Curve

Random failures Early failures Wearout failures 0. 2 Failure Rate r(t) 0. 15 0. 1 0. 05 20 40 60 80 Failure rate r(t) versus t. 100

Reliability - R(t) • The probability that the component experiences no failure during the time interval (0, t). • Example: exponential distribution

Unreliability - F(t) • The probability that the component experiences the first failure during (0, t). • Example: exponential distribution

Failure Density - f(t) (exponential distribution)

Failure Rate - r(t) • The probability that the component fails per unit time at time t, given that the component has survived to time t. • Example: The component with a constant failure rate is considered as good as new, if it is functioning.

Mean Time to Failure - MTTF

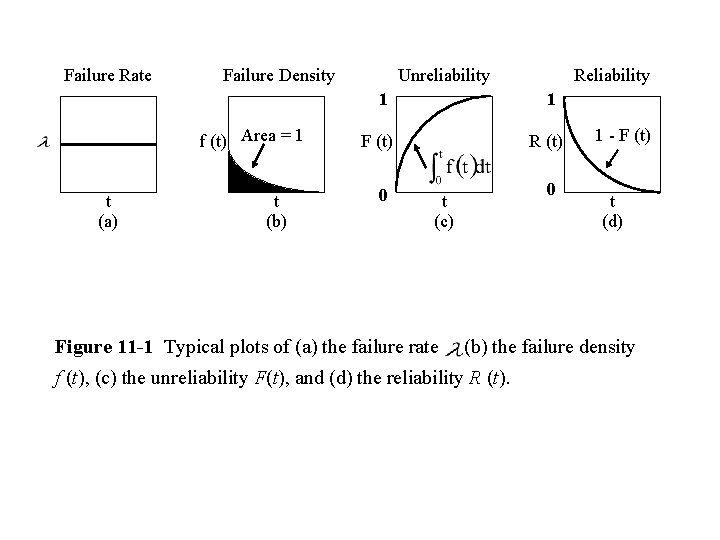
Failure Rate Failure Density Unreliability 1 f (t) Area = 1 t (a) t (b) 1 F (t) 0 Reliability R (t) 0 t (c) Figure 11 -1 Typical plots of (a) the failure rate 1 - F (t) t (d) (b) the failure density f (t), (c) the unreliability F(t), and (d) the reliability R (t).

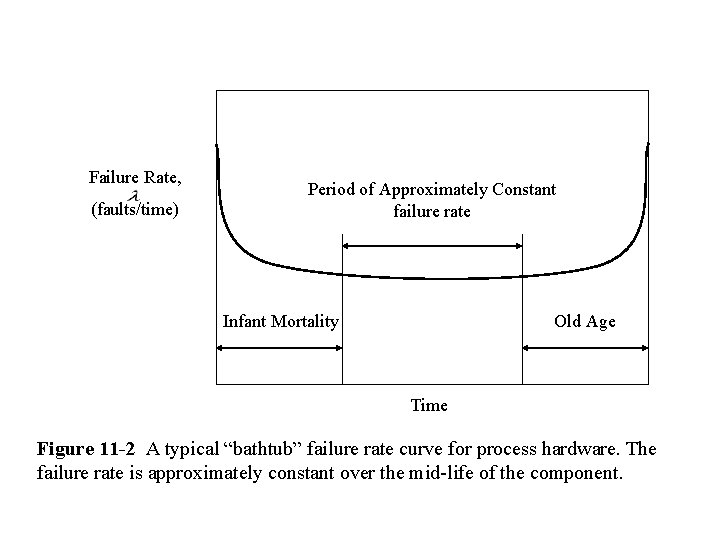
Failure Rate, (faults/time) Period of Approximately Constant failure rate Infant Mortality Old Age Time Figure 11 -2 A typical “bathtub” failure rate curve for process hardware. The failure rate is approximately constant over the mid-life of the component.

TABLE 11 -1: FAILURE RATE DATA FOR VARIOUS SELECTED PROCESS COMPONENTS 1 Instrument Fault/year Controller Control valve Flow measurement (fluids) 0. 29 0. 60 1. 14 Flow measurement (solids) Flow switch Gas - liquid chromatograph 3. 75 1. 12 30. 6 Hand valve Indicator lamp Level measurement (liquids) 0. 13 0. 044 1. 70 Level measurement (solids) Oxygen analyzer p. H meter 6. 86 5. 65 5. 88 Pressure measurement Pressure relief valve Pressure switch 1. 41 0. 022 0. 14 Solenoid valve Stepper motor Strip chart recorder 0. 42 0. 044 0. 22 Thermocouple temperature measurement Thermometer temperature measurement Valve positioner 0. 52 0. 027 0. 44 1 Selected from Frank P. Lees, Loss Prevention in the Process Industries (London: Butterworths, 1986), p. 343.

A System with n Components in Parallel • Unreliability • Reliability

A System with n Components in Series • Reliability • Unreliability

Upper Bound of Unreliability for Systems with n Components in Series

Pressure Switch Alarm at P > PA PIC Pressure Feed Solenoid Valve Reactor Figure 11 -5 A chemical reactor with an alarm and inlet feed solenoid. The alarm and feed shutdown systems are linked in parallel.

Alarm System • The components are in series Faults/years

Shutdown System • The components are also in series:

The Overall Reactor System • The alarm and shutdown systems are in parallel:

The Failure-to-Repair Process

Repair Probability - G(t) • The probability that repair is completed before time t, given that the component failed at time zero. • If the component is non-repairable

Repair Density - g(t)

Repair Rate - m(t) • The probability that the component is repaired per unit time at time t, given that the component failed at time zero and has been failed to time t. • If the component is non-repairable

Mean Time to Repair - MTTR

The Whole Process

Availability - A(t) • The probability that the component is normal at time t. • For non-repairable components • For repairable components

Unavailability - Q(t) • The probability that the component fails at time t. • For non-repairable components • For repairable components

Unconditional Repair Density, w(t) The probability that a component fails per unit time at time t, given that it jumped into the normal state at time zero. Note, for non-repairable components.

Unconditional Repair Density, v(t) The probability that the component is repaired per unit time at time t, give that it jumped into the normal state at time zero.

Conditional Failure Intensity, λ(t) The probability that the component fails per unit time, given that it is in the normal state at time zero and normal at time t. In general , λ(t)≠r(t). For non-repairable components, λ(t) = r(t). However, if the failure rate is constant (λ) , then λ(t) = r(t) = λ for both repairable and nonrepairable components.

Conditional Repair Intensity, µ(t) The probability that a component is repaired per unit time at time t, given that it is jumped into the normal state at time zero and is failed at time t, For non-repairable component, µ(t)=m(t)=0. For constant repair rate m, µ(t)=m.

ENF over an interval, W(t 1, t 2 ) Expected number of failures during (t 1, t 2) given that the component jumped into the normal state at time zero. For non-repairable components

SHORT-CUT CALCULATION METHODS Information Required Approximation of Event Unavailability When time is long compared with MTTR and can be made, Where, is the MTTR of component j. , the following approximation

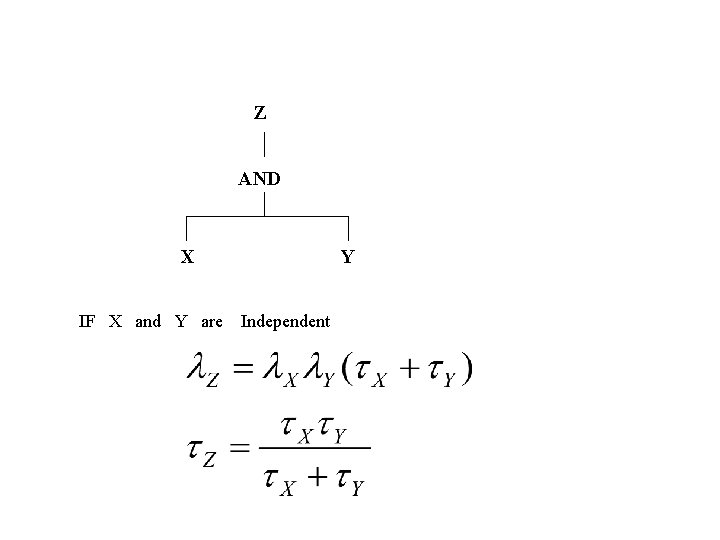
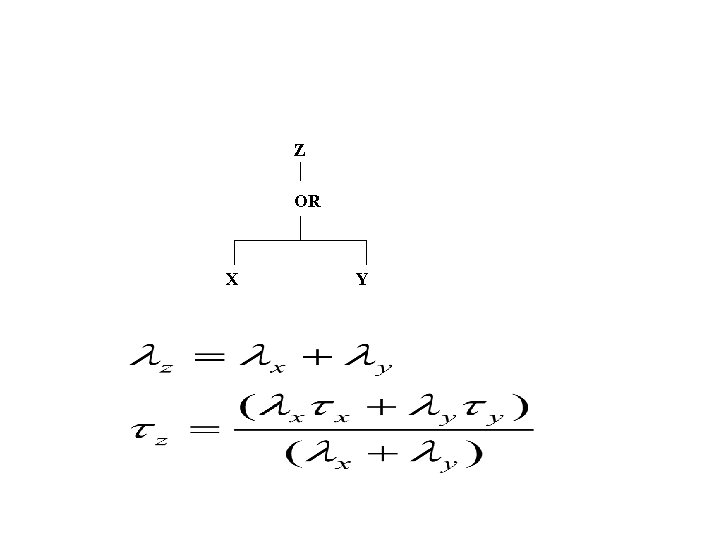
Z AND X IF X and Y are Y Independent

Z OR X Y

COMPUTATION OF ACROSS LOGIC GATES 2 INPUTS AND GATES OR GATES 3 INPUTS n INPUTS

CUT SET IMPORTANCE The importance of a cut set K is defined as Where, is the probability of the top event. as the conditional probability that the cut set top event has occurred. may be interpreted occurs given that the PRIMAL EVENT IMPORTANCE The importance of a primal event is defined as or Where, the sum is taken over all cut sets which contain primal event.

[ EXAMPLE ] As an example , consider the tree used in the section on cut sets. The cut sets for this tree are (1) , (2) , (6) , (3, 4) , (3, 5). The following data are given from which we compute the unavailabilities for each event. 1 2 3 4 5 6 . 16. 2 1. 4 30 5. 5 1. 5 E-5 (. 125) 7 E-4 (6) 1. 1 E-4 (1) 5. 5 E-5 (. 5) 2. 4 E-6 3. 0 E-6 9. 8 E-4 3. 3 E-3 5. 5 E-4 2. 75 E-5 Now, compute the probability of occurrence for each cut set and top event probability. (1) 2. 4 E-6 (2) 3. 0 E-6 (6) 2. 75 E-5 (3, 4) 3. 23 E-6 (3, 5) 5. 39 E-7 3. 67 E-5