TIF 4216 Matematika Diskrit Pencacahan Counting Justanintermezzo Pengelola

TIF 4216 Matematika. Diskrit

Pencacahan. Counting

Justanintermezzo Pengelola Pantai Hanakapiai, Hawaii memperingatkan pengunjung agar tidak mendekati kawasan air, dan menegaskan peringatan tersebut dengan membuat menyusun tallymarks yang berfungsi menghitung secara diskrit jumlah korban yang nekat

Macam Pencacahan Tally. Marks

Kombinatorial • Cabang matematika yang mempelajari pengaturan objek • Jumlah cara/solusi yang diperoleh dari himpunannya • Contoh: 1. Plat mobil di negara X teridiri dari 5 angka dan diikuti 2 huruf. Angka pertama tidak boleh 0. Berapa banyak nomor plat mobil yang dapat di buat. 2. Password sebuah sistem komputer panjang nya 6 – 8 karakter. Tiap karakter boleh berupa huruf dan atau angka. Tidak case sensitive. Berapa banyak password yang dapat dibuat? Matematika Komputasi 5

Kombinatorial • Kombinatorial didasarkan pada hasil yang di peroleh dari percobaan: • Contoh: • Melempar dadu Enam hasil percobaan yang mungkin untuk pelemparan dadu adalah muka dadu 1, 2, 3, 4, 5, atau 6. • Melempar uang koin uang Rp. 100 Hasil percobaan melempar koin 100 ada dua kemungkinan: muka koin gambar rumah gadang atau koin gambar wayang. Matematika Komputasi 6

Case Password with 6 character, consist of letter and number abcdef aaaade a 123 fr 123789 34 qwer. . . COMBINATION

Kombinatorial cabang matematika untuk menghitung jumlah penyusunan objek-objek tanpa harus mengenumerasi semua kemungkinan susunannya

Kaidah Dasar Menghitung Rule of Sum (Kaidah Penjumlahan) Misal: Percobaan 1: p hasil Percobaan 2: q hasil maka: Perc. 1 atau Perc. 2: p + q hasil Rule of Product (Kaidah Perkalian) Misal: Percobaan 1: p hasil Percobaan 2: q hasil maka: Perc. 1 dan Perc. 2: p x q hasil

Latihan 1 Dari seluruh mahasiswa Tif angkatan 2010, terdapat 250 laki 2 dan 150 perempuan. Dengan tanpa memperhitungkan gender, berapa cara memilih satu ketua himpunan? Solusi: 250 + 150 = 400 cara

Latihan 2 Dari seluruh mahasiswa Tif angkatan 2010, terdapat 300 peminat jaringan dan 100 peminat vision. Dari setiap bidang minat akan dipilih 1 wakil untuk ikut seminar, berapa cara memilih dua orang peserta seminar? Solusi: 300 x 100 = 30. 000 cara

Perluasan kaidah menghitung • Dapat mengandung lebih dari dua percobaan. • Jika n buah percobaan masing-masing mempunyai p 1, p 2, p 3, . . . pn. hasil percobaan tidak bergantung pada percobaan sebelumnya: • Rule of sum – p 1 x p 2 x p 3. . . x pn – Hal. 231 Rinaldi Munir • Rule of product – P 1 + p 2 + p 3. . . + p 4 – Hal. 232 Rinaldi Munir Matematika Komputasi 12

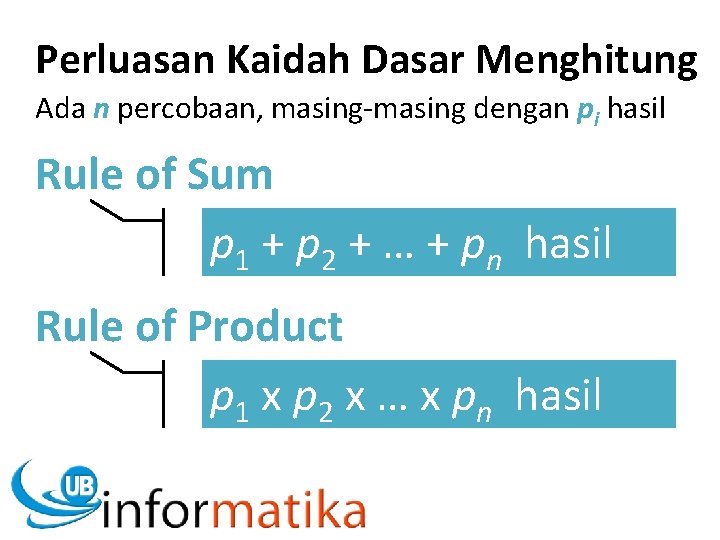
Perluasan Kaidah Dasar Menghitung Ada n percobaan, masing-masing dengan pi hasil Rule of Sum p 1 + p 2 + … + pn hasil Rule of Product p 1 x p 2 x … x pn hasil

Latihan 3 Dari seluruh pemain Arema yang siap bertanding, terdapat 1 kiper, 3 bek, 4 gelandang dan 3 penyerang. Dengan tanpa memperhitungkan posisinya, berapa cara memilih satu kapten tim? Solusi: 1 + 3 + 4 + 3 = 11 cara

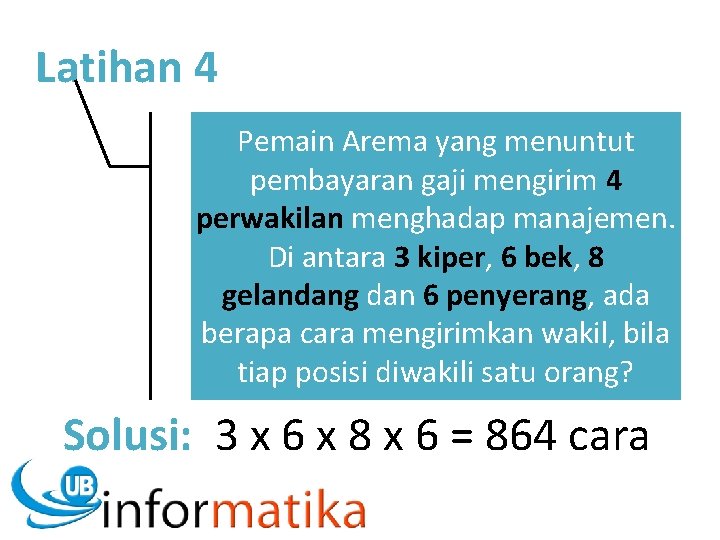
Latihan 4 Pemain Arema yang menuntut pembayaran gaji mengirim 4 perwakilan menghadap manajemen. Di antara 3 kiper, 6 bek, 8 gelandang dan 6 penyerang, ada berapa cara mengirimkan wakil, bila tiap posisi diwakili satu orang? Solusi: 3 x 6 x 8 x 6 = 864 cara

Soal 2 Password pada sebuah sistem komputer panjangnya enam sampai delapan karakter. Tiap karakter boleh berupa huruf atau angka; TIDAK case sensitive. Berapa banyak kombinasi password yang dapat dibuat?

Pembahasan Soal 8 digit 1 2 kemungkinan: 0 / 1 Terdapat 1 byte string yang berupa bilangan biner. Berapa banyak string yang dapat dibentuk? Solusi: 2 x 2 x 2 = 28 = 256 cara

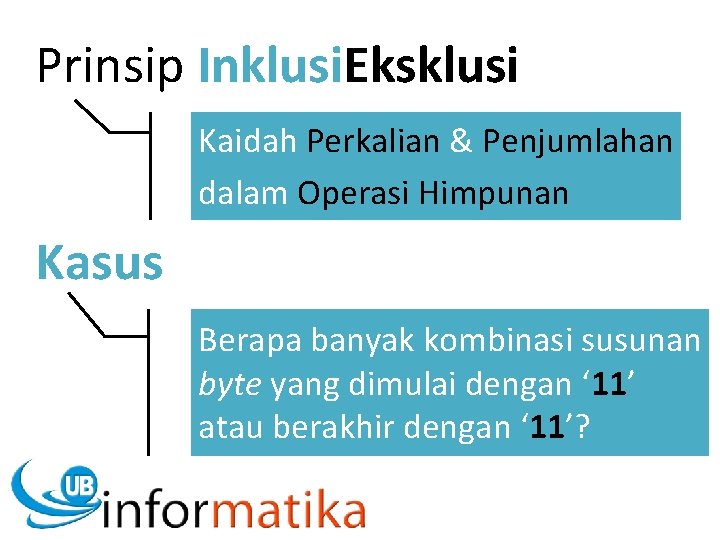
Prinsip Inklusi. Eksklusi Kaidah Perkalian & Penjumlahan dalam Operasi Himpunan Kasus Berapa banyak kombinasi susunan byte yang dimulai dengan ‘ 11’ atau berakhir dengan ‘ 11’?

! AT G N I Prinsip Divide & Conquer A = himpunan byte yang dimulai dengan ‘ 11’, B = himpunan byte yang diakhiri dengan ‘ 11’ |A| = |B| = 1 x 2 x 2 = 64 2 x 2 x 2 x 1 x 1 = 64 ? |A B| = 128

|A B| = 1 x 2 x 2 x 1 x 1 = 16 |A B| = |A| + |B| - |A B| = 64 + 64 - 16 = 112

P igeon. Hole P rinciple

9 holes 10 pigeons Bila terdapat n obyek yang diletakkan pada m buah tempat, dengan nilai n > m, maka: Paling tidak, satu tempat berisi lebih dari 1 obyek 1 2 5 8 2 1 4 3 4 7 6 9 5 8 7 10 3 6 9

Pigeon-holeprinciple Dirichlet drawer principle 1834 Gustav. Lejeune. Dirichlet (1805 – 1859)

Case 1. Di antara tiga orang, maka pasti ada dua orang yang berjenis kelamin sama 2. Dari 32 orang, pasti ada 2 orang yang memiliki tanggal lahir yang sama. 3. Bila sebuah tim sepakbola menang 12 -0, pasti ada pemain yang mencetak lebih dari satu gol a l Je ! n a k s

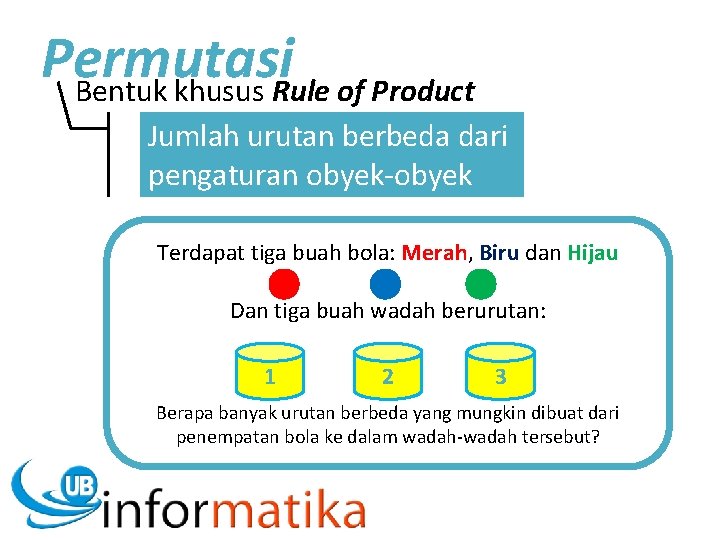
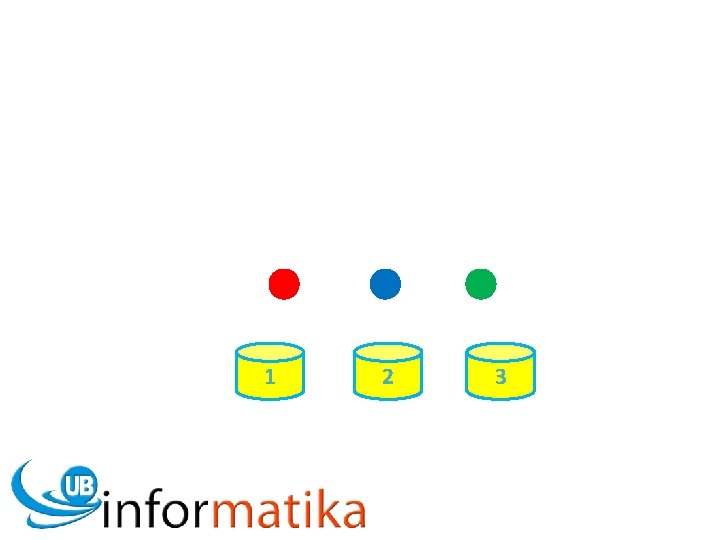
Permutasi Bentuk khusus Rule of Product Jumlah urutan berbeda dari pengaturan obyek-obyek Terdapat tiga buah bola: Merah, Biru dan Hijau Dan tiga buah wadah berurutan: 1 2 3 Berapa banyak urutan berbeda yang mungkin dibuat dari penempatan bola ke dalam wadah-wadah tersebut?

1 2 3

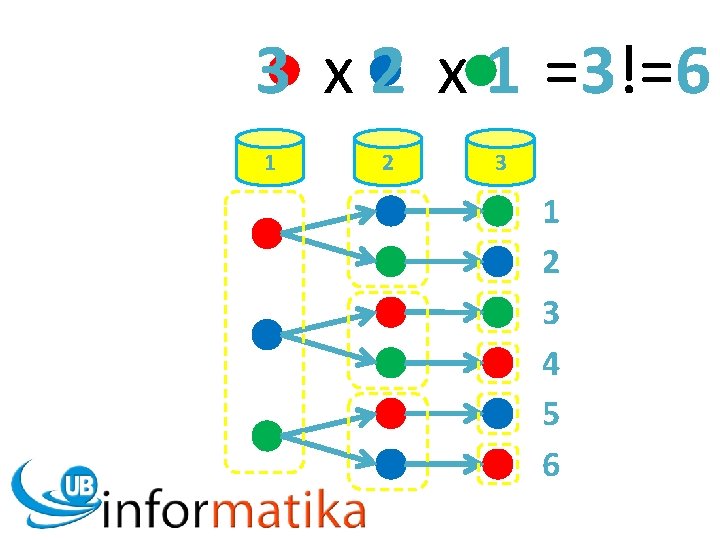
3 x 2 x 1 =3!=6 1 2 3 4 5 6

Permutasi n obyek P(n, n) = n x (n-1) x (n-2) x. . . 2 x 1 P(n, n) = n ! Permutasi r dari n elemen P(n, r) = n x (n-1) x (n-2) x. . . (n-(r-1)) n ! P(n, r) = (n-r) !

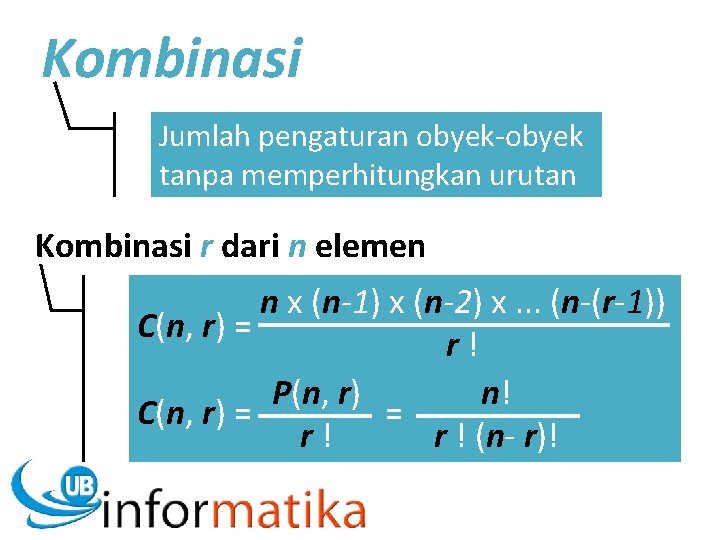
Kombinasi Jumlah pengaturan obyek-obyek tanpa memperhitungkan urutan Kombinasi r dari n elemen n x (n-1) x (n-2) x. . . (n-(r-1)) C(n, r) = r ! n! P(n, r) C(n, r) = = r ! (n- r)! r !

Soal 3 Di antara 10 orang mahasiswa Teknik Informatika Angkatan 2010, berapa banyak cara membentuk sebuah perwakilan beranggotakan 5 orang sedemikian sehingga: a. mahasiswa bernama A selalu termasuk di dalamnya; b. mahasiswa bernama A tidak termasuk di dalamnya; c. mahasiswa bernama A selalu termasuk di dalamnya, tetapi B tidak; d. mahasiswa bernama B selalu termasuk di dalamnya, tetapi A tidak; e. mahasiswa bernama A dan B termasuk di dalamnya; f. setidaknya salah satu dari mahasiswa yang bernama A atau B termasuk di dalamnya.

Terimakaish

Kombinatioral - Permutasi - Kombinasi 34

Permutasi • Mengabungkan beberapa objek dari suatu grup dengan memperhatikan urutan • Permutasi dari n unsur yang berbeda x 1, x 2, …, xn adalah pengurutan dari n unsur tersebut. • Contoh: ABC; Tentukan permutasi dari tiga huruf yang berbeda! Permutasi: ABC, ACB, BAC, BCA, CAB, CBA # 6 permutasi huruf ABC 35

Permutasi • Permutasi-r dari n unsur yang berbeda x 1, x 2, …, xn adalah pengurutan dari sub himpunan dengan r anggota dari himpunan {x 1, x 2, …, xn} • Dinotasikan P(n, r) • Contoh: Tentukan permutasi-3 dari 5 huruf yang berbeda, ABCDE! Banyaknya permutasi-3 dari 5 : 60 ABC ABD ABE ACB ACD ACE ADB ADC ADE AEB AEC AED . . . . ECA ECB ECD EDA EDB EDC 36

Permutasi • Banyaknya permutasi-r dari n unsur yang berbeda: • P(n, r) = n!/(n-r)! • Contoh: Permutasi-3 dari 5 huruf yang berbeda, ABDCE P(5, 3) = 5!/(5 -3)! = 5 × 4 × 3 = 60 37

Kombinasi • Menggabungkan beberapa objek dari suatu grup tanpa memperhatikan urutan • Kombinasi-r dari n unsur yang berbeda x 1, x 2, …, xn adalah seleksi tak terurut r anggota dari himpunan {x 1, x 2, …, xn} • Banyaknya kombinasi-r dari n unsur dinotasikan C(n, r) • Contoh: Kombinasi-3 dari huruf ABCDE adalah: ABC ABD ABE ACD ACE ADE BCD BCE BDE CDE Kombinasi-3 dari 5 huruf : 10 38

Kombinasi • Banyaknya kombinasi-r dari n unsur yang berbeda adalah C(n, r) = n!/(n-r)!. r! • Contoh: Kombinasi-3 dari 5 huruf berbeda, ABCDE adalah C(5 -3) = 5!/(5 -3)!. 3! = 5!/2!. 3! = 5 × 4/2 = 10 39

Kombinasi • Contoh: Berapa banyak cara sebuah panitia yang terdiri dari 2 mahasiswa dan 3 mahasiswi yang bisa dipilih dari 5 mahasiswa dan 6 mahasiswi? • Jawab: Pertama: memilih 2 mahasiswa dari 5 mahasiswa C(5, 2) = 10 Kedua: memilih 3 mahasiswi dari 6 mahasiswi C(6, 3) = 20 Sehingga terdapat 10 × 20 = 200 cara 40

Terimakasih