There are two things to aim at in

“There are two things to aim at in life: first, to get what you want; and, after that, to enjoy it. Only the wisest of mankind achieve the second. ” Logan Pearsall Smith, Afterthought (1931), “Life and Human Nature”

Chapter 3 Crystal Geometry and Structure Determination

Contents Crystal, Lattice and Motif Symmetry Crystal systems Bravais lattices Miller Indices Structure Determination

Crystal ? A 3 D translationaly periodic arrangement of atoms in space is called a crystal.

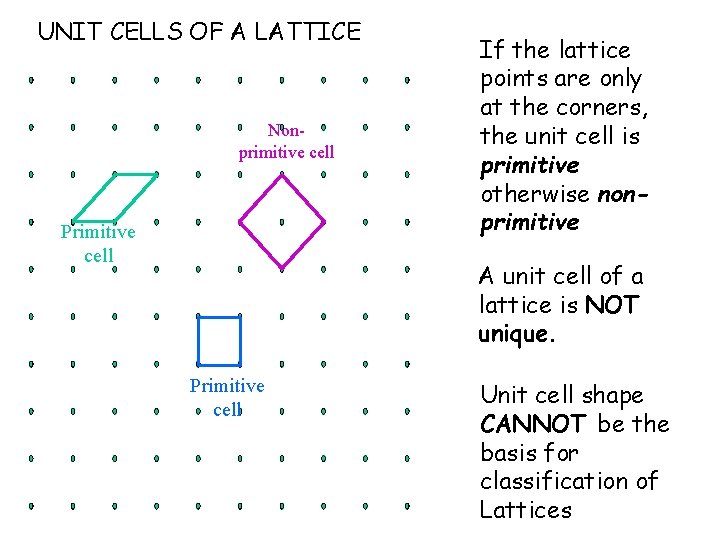
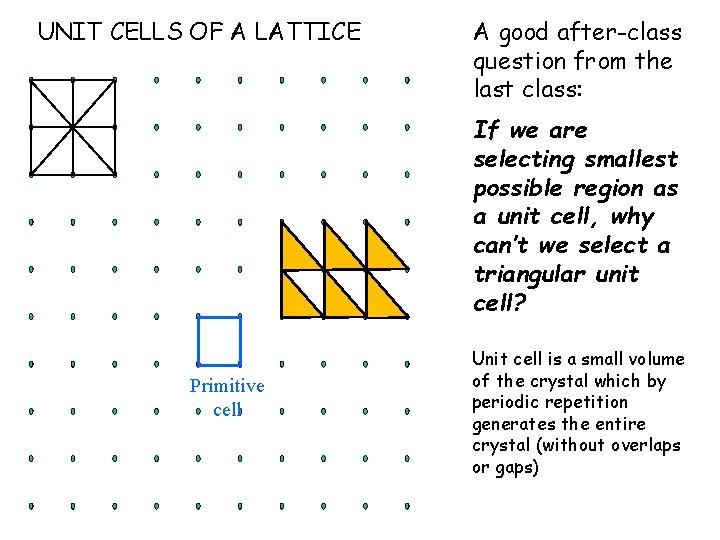
Unit cell description : 1 Translational Periodicity One can select a small volume of the crystal which by periodic repetition generates the entire crystal (without overlaps or gaps) Unit Cell

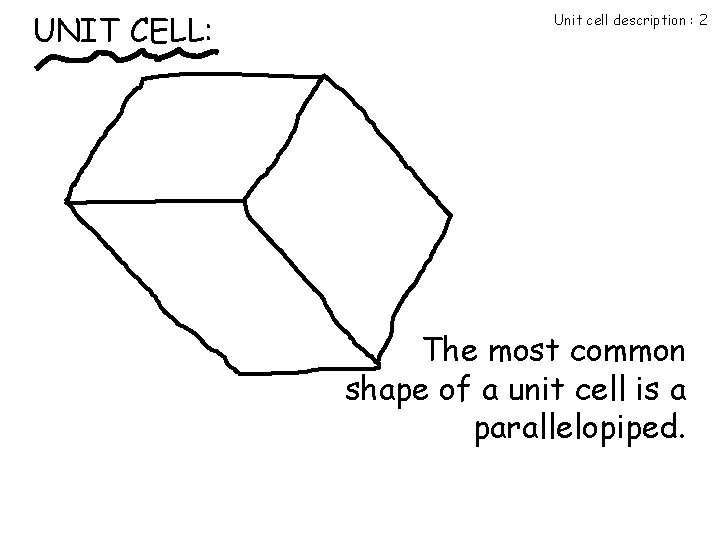
UNIT CELL: Unit cell description : 2 The most common shape of a unit cell is a parallelopiped.

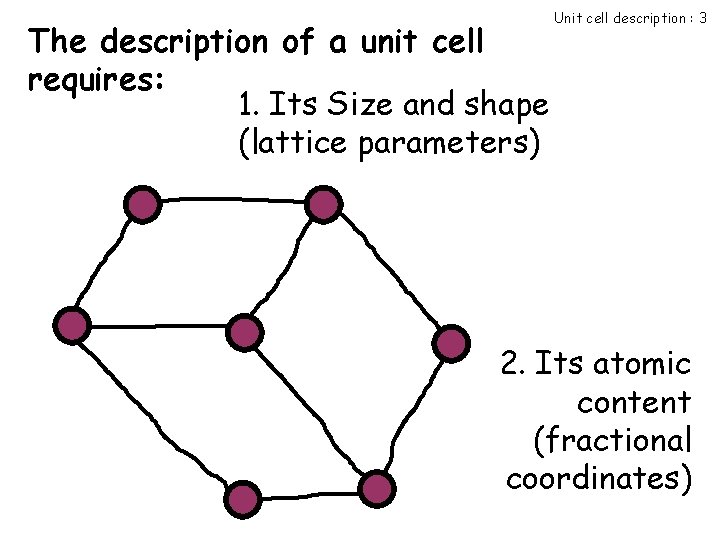
The description of a unit cell requires: 1. Its Size and shape (lattice parameters) Unit cell description : 3 2. Its atomic content (fractional coordinates)

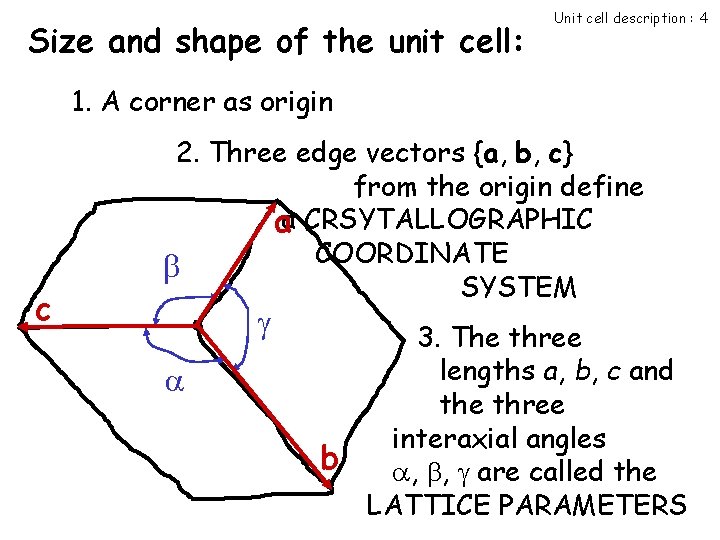
Size and shape of the unit cell: Unit cell description : 4 1. A corner as origin c 2. Three edge vectors {a, b, c} from the origin define aa CRSYTALLOGRAPHIC COORDINATE SYSTEM b 3. The three lengths a, b, c and the three interaxial angles , , are called the LATTICE PARAMETERS

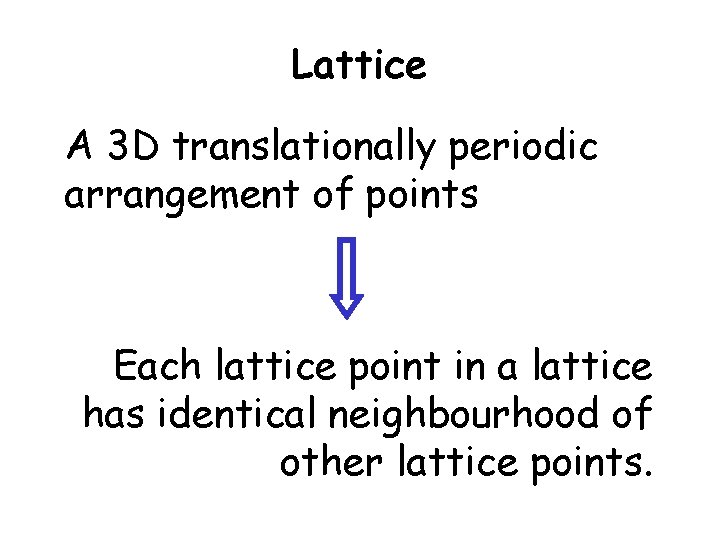
Lattice? A 3 D translationally periodic arrangement of points in space is called a lattice.

Lattice A 3 D translationally periodic arrangement of points Each lattice point in a lattice has identical neighbourhood of other lattice points.

Classification of lattice The Seven Crystal System And The Fourteen Bravais Lattices

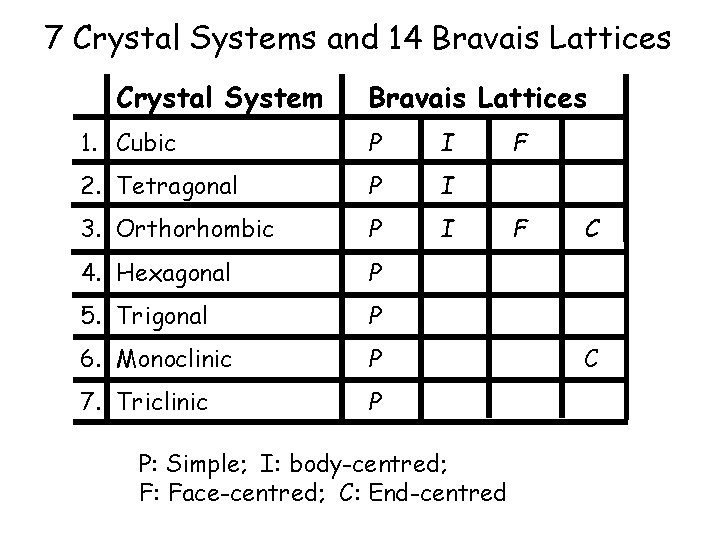
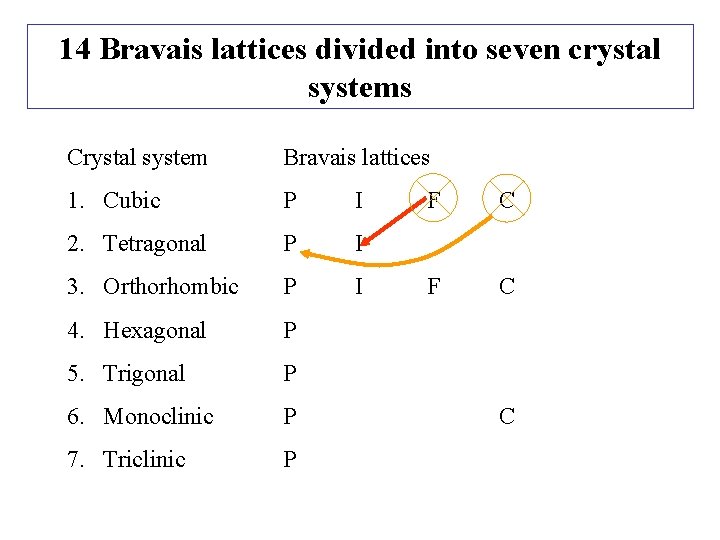
7 Crystal Systems and 14 Bravais Lattices Crystal System Bravais Lattices 1. Cubic P I 2. Tetragonal P I 3. Orthorhombic P I 4. Hexagonal P 5. Trigonal P 6. Monoclinic P 7. Triclinic P P: Simple; I: body-centred; F: Face-centred; C: End-centred F F C C

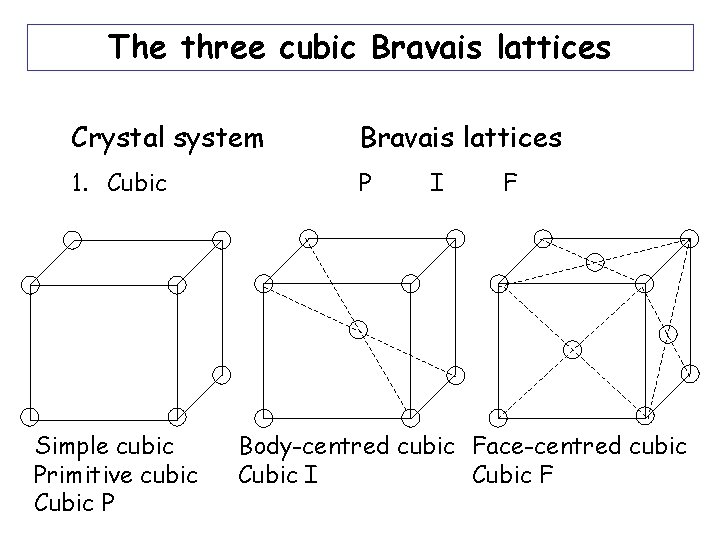
The three cubic Bravais lattices Crystal system Bravais lattices 1. Cubic P Simple cubic Primitive cubic Cubic P I F Body-centred cubic Face-centred cubic Cubic I Cubic F

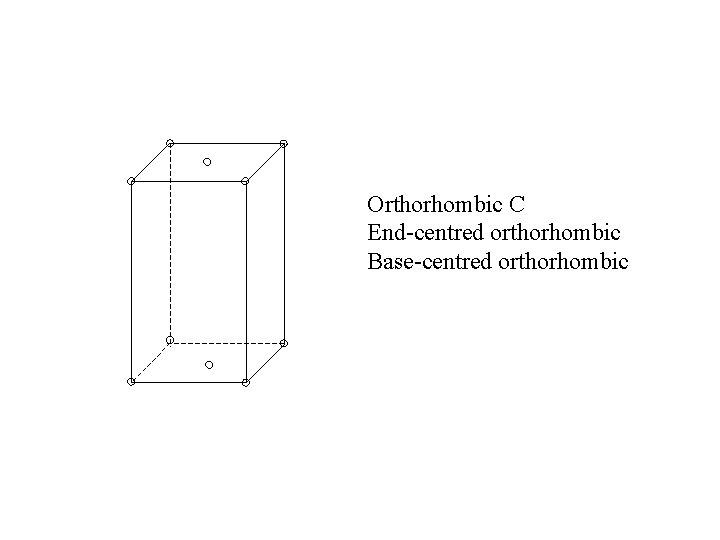
Orthorhombic C End-centred orthorhombic Base-centred orthorhombic

15/87 Cubic Crystals? a=b=c; = = =90

7 crystal Systems Unit Cell Shape Crystal System 1. a=b=c, = = =90 Cubic 2. a=b c, = = =90 Tetragonal 3. a b c, = = =90 Orthorhombic 4. a=b c, = = 90 , =120 Hexagonal 5. a=b=c, = = 90 Rhombohedral OR Trigonal 6. a b c, = =90 Monoclinic 7. a b c, Triclinic

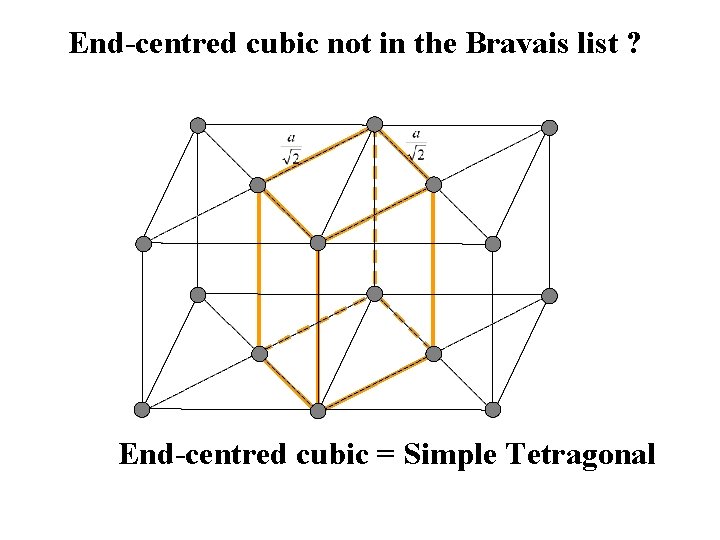
Why half the boxes are empty? Crystal System Bravais Lattices 1. Cubic P I 2. Tetragonal P I 3. Orthorhombic P I 4. Hexagonal P 5. Trigonal P 6. Monoclinic P 7. Triclinic P F ? F C E. g. Why cubic C is absent? C

End-centred cubic not in the Bravais list ? End-centred cubic = Simple Tetragonal

14 Bravais lattices divided into seven crystal systems Crystal system Bravais lattices 1. Cubic P I 2. Tetragonal P I 3. Orthorhombic P I 4. Hexagonal P 5. Trigonal P 6. Monoclinic P 7. Triclinic P F C C

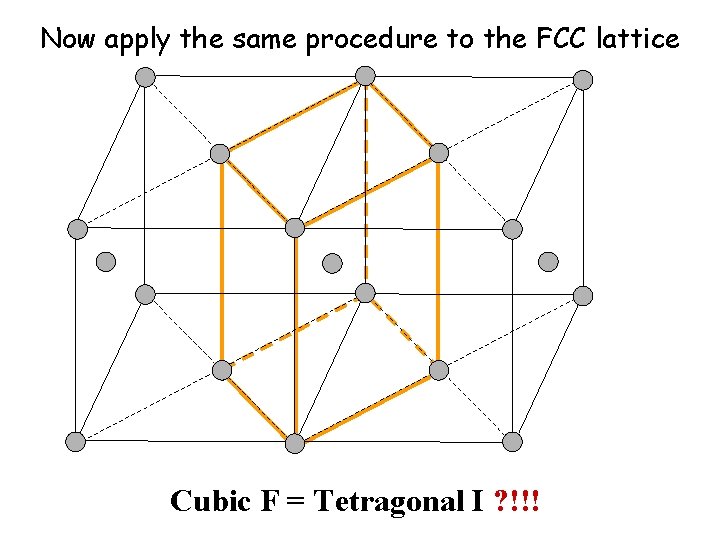
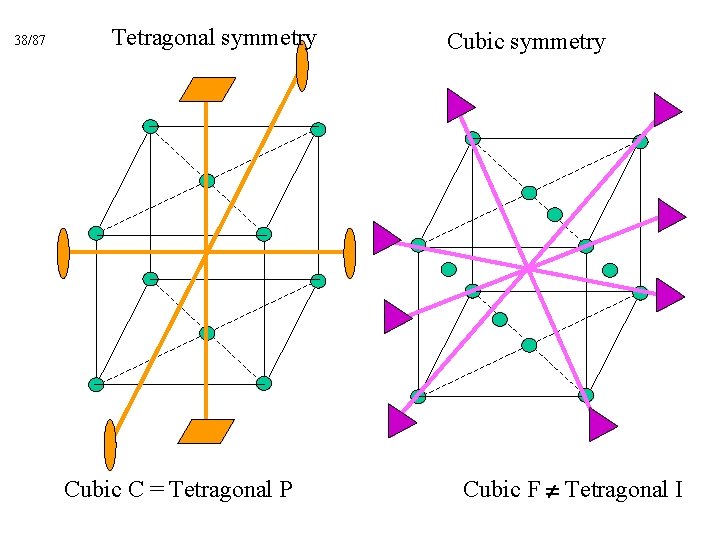
Now apply the same procedure to the FCC lattice Cubic F = Tetragonal I ? !!!

14 Bravais lattices divided into seven crystal systems Crystal system Bravais lattices 1. Cubic P I 2. Tetragonal P I 3. Orthorhombic P I 4. Hexagonal P 5. Trigonal P 6. Monoclinic P 7. Triclinic P F C C

History: ML Frankenheim 1801 -1869 1835: 1856: 15 lattices X 14 lattices Couldn’t find his photo on the net IIT-Delhi Auguste Bravais 1811 -1863 1850: 14 lattices 26 th July 2013: AML 120 Class Sem I 2013 -2014 13 lattices !!!

UNIT CELLS OF A LATTICE Nonprimitive cell Primitive cell If the lattice points are only at the corners, the unit cell is primitive otherwise nonprimitive A unit cell of a lattice is NOT unique. Primitive cell Unit cell shape CANNOT be the basis for classification of Lattices

End of Lec 3 (Lec 1 on crystallography)

UNIT CELLS OF A LATTICE A good after-class question from the last class: If we are selecting smallest possible region as a unit cell, why can’t we select a triangular unit cell? Primitive cell Unit cell is a small volume of the crystal which by periodic repetition generates the entire crystal (without overlaps or gaps)

Why can’t the Face. Centred Cubic lattice (Cubic F) be considered as a Body-Centred Tetragonal lattice (Tetragonal I) ?

What is the basis for classification of lattices into 7 crystal systems and 14 Bravais lattices?

Lattices are classified on the basis of their symmetry

Symmetry? If an object is brought into selfcoincidence after some operation it said to possess symmetry with respect to that operation.

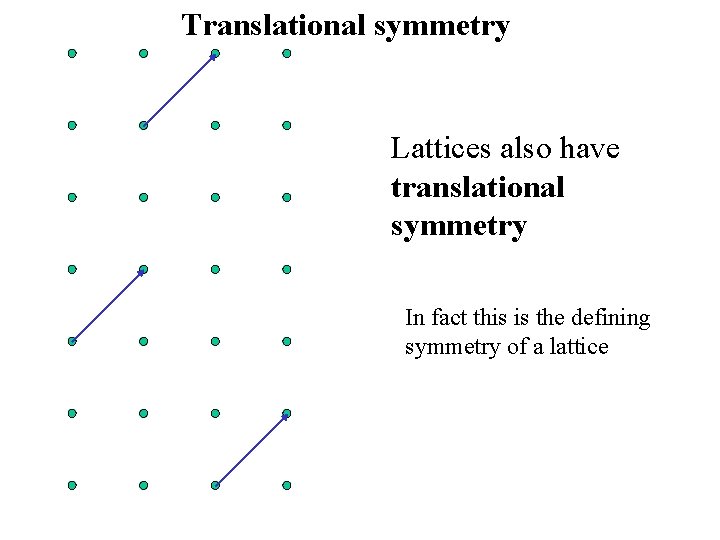
Translational symmetry Lattices also have translational symmetry In fact this is the defining symmetry of a lattice

Rotation Axis If an object come into self-coincidence through smallest non-zero rotation angle of then it is said to have an nfold rotation axis where =180 n=2 2 -fold rotation axis =90 n=4 4 -fold rotation axis

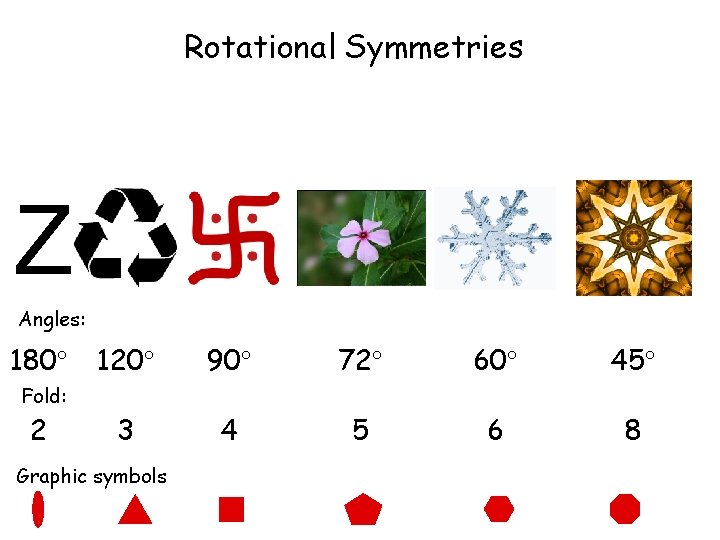
Rotational Symmetries Z Angles: 180 120 90 72 60 45 3 4 5 6 8 Fold: 2 Graphic symbols

Crsytallographic Restriction 5 -fold symmetry or Pentagonal symmetry is not possible for Periodic Tilings Symmetries higher than 6 -fold also not possible Only possible rotational symmetries for lattices 2 3 4 5 6 7 8 9…

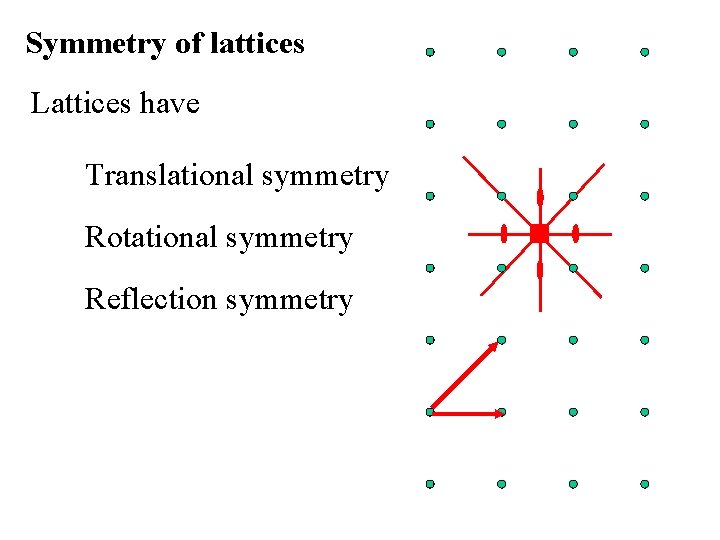
Symmetry of lattices Lattices have Translational symmetry Rotational symmetry Reflection symmetry

Point Group and Space Group The group of all symmetry elements of a crystal except translations (e. g. rotation, reflection etc. ) is called its POINT GROUP. The complete group of all symmetry elements including translations of a crystal is called its SPACE GROUP

Classification of Lattices Crystal systems and Bravais Lattices Classification of lattices Based on the point group symmetry alone (i. e. excluding translational symmetry 7 types of lattices 7 crystal systems Based on the space group symmetry, i. e. , rotational, reflection and translational symmetry 14 types of lattices 14 Bravais lattices

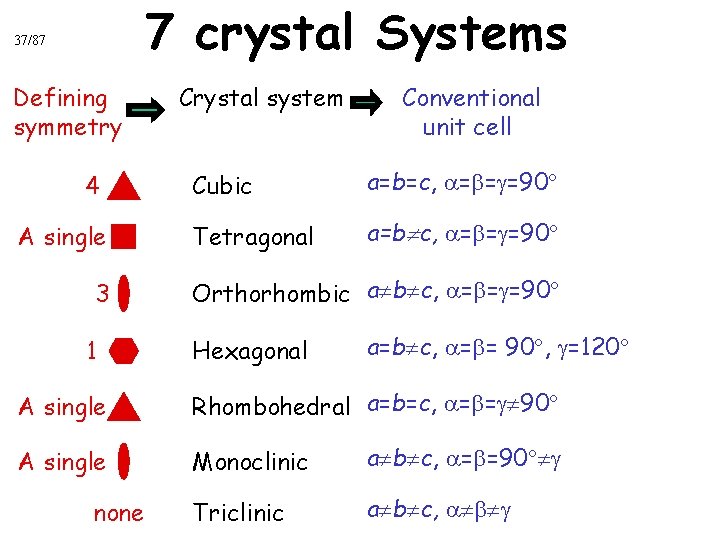
7 crystal Systems 37/87 Defining symmetry 4 A single 3 1 Crystal system Conventional unit cell Cubic a=b=c, = = =90 Tetragonal a=b c, = = =90 Orthorhombic a b c, = = =90 Hexagonal a=b c, = = 90 , =120 A single Rhombohedral a=b=c, = = 90 A single Monoclinic a b c, = =90 Triclinic a b c, none

38/87 Tetragonal symmetry Cubic C = Tetragonal P Cubic symmetry Cubic F Tetragonal I

End of Lec 4 on 30. 07. 2013 Lec 2 on crystallography

Crystal Lattice A 3 D translationally periodic arrangement of atoms A 3 D translationally periodic arrangement of points

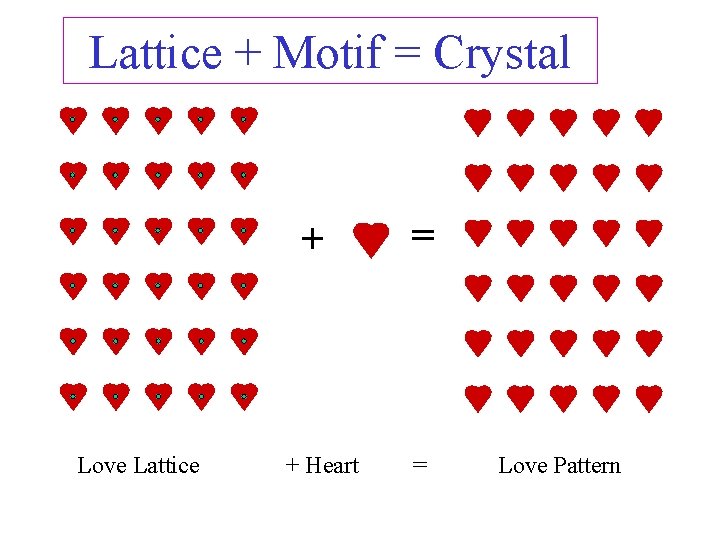
What is the relation between the two? Crystal = Lattice + Motif or basis: an atom or a group of atoms associated with each lattice point

Crystal=lattice+basis Lattice: the underlying periodicity of the crystal, Basis: atom or group of atoms associated with each lattice points Lattice: how to repeat Motif: what to repeat

Lattice + Motif = Crystal + Love Lattice + Heart = = Love Pattern

Air, Water and Earth by M. C. Esher

Every periodic pattern (and hence a crystal) has a unique lattice associated with it

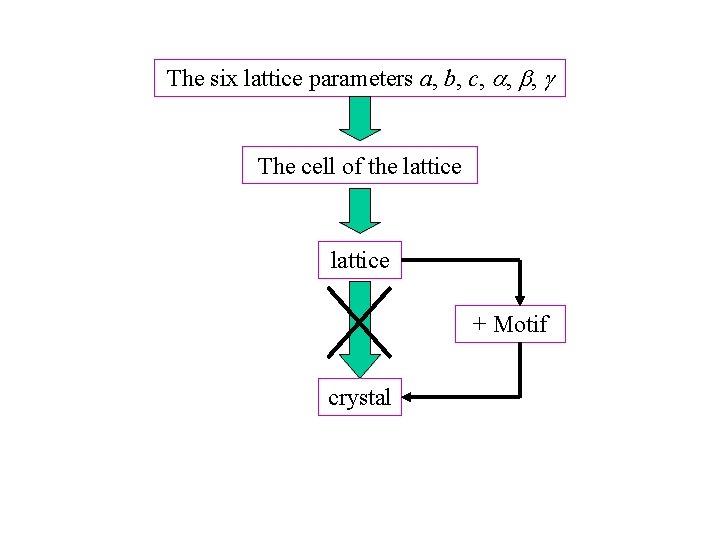
The six lattice parameters a, b, c, , , The cell of the lattice + Motif crystal

Richard P. Feynman Nobel Prize in Physics, 1965

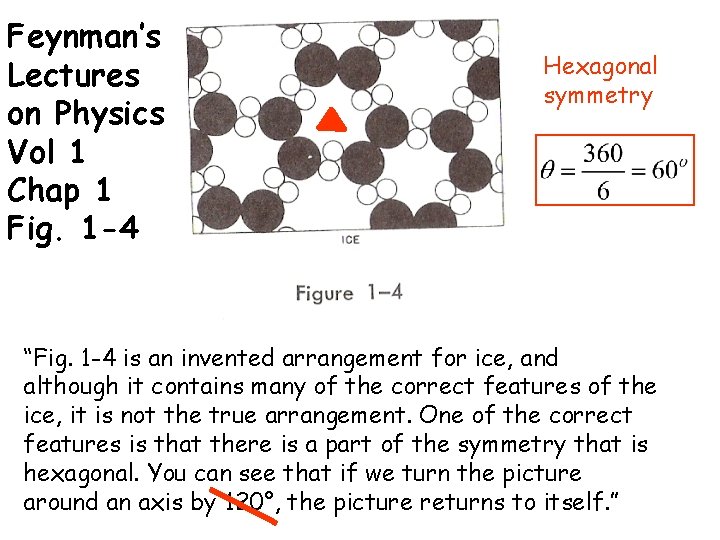
Feynman’s Lectures on Physics Vol 1 Chap 1 Fig. 1 -4 Hexagonal symmetry “Fig. 1 -4 is an invented arrangement for ice, and although it contains many of the correct features of the ice, it is not the true arrangement. One of the correct features is that there is a part of the symmetry that is hexagonal. You can see that if we turn the picture around an axis by 120°, the picture returns to itself. ”

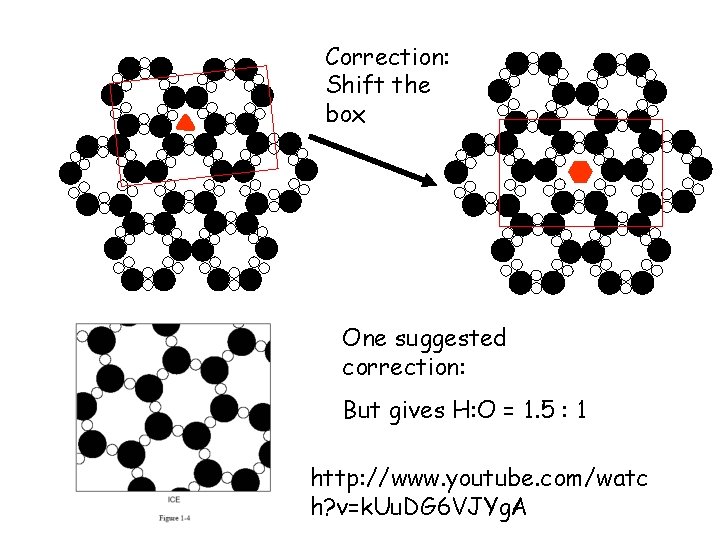
Correction: Shift the box One suggested correction: But gives H: O = 1. 5 : 1 http: //www. youtube. com/watc h? v=k. Uu. DG 6 VJYg. A

The errata has been accepted by Michael Gottlieb of Caltech and the corrections will appear in future editions Website www. feynmanlectures. info

QUESTIONS?

Miller Indices 1 Miller Indices of directions and planes William Hallowes Miller (1801 – 1880) University of Cambridge

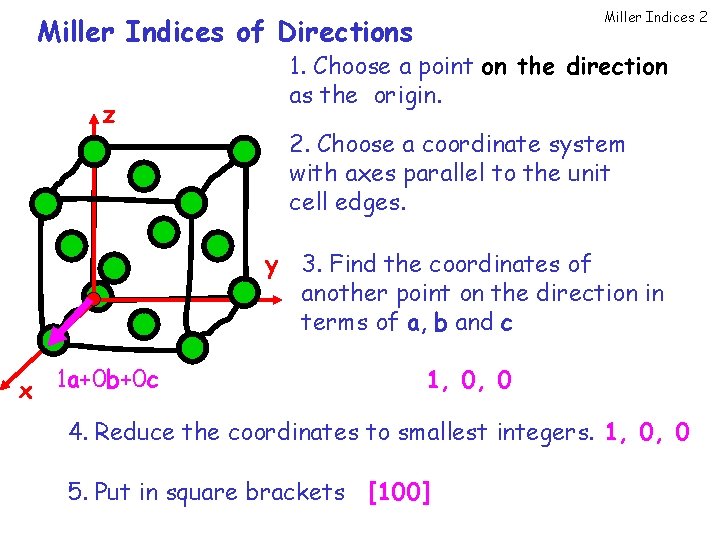
Miller Indices 2 Miller Indices of Directions z 1. Choose a point on the direction as the origin. 2. Choose a coordinate system with axes parallel to the unit cell edges. y 3. Find the coordinates of another point on the direction in terms of a, b and c x 1 a+0 b+0 c 1, 0, 0 4. Reduce the coordinates to smallest integers. 1, 0, 0 5. Put in square brackets [100]

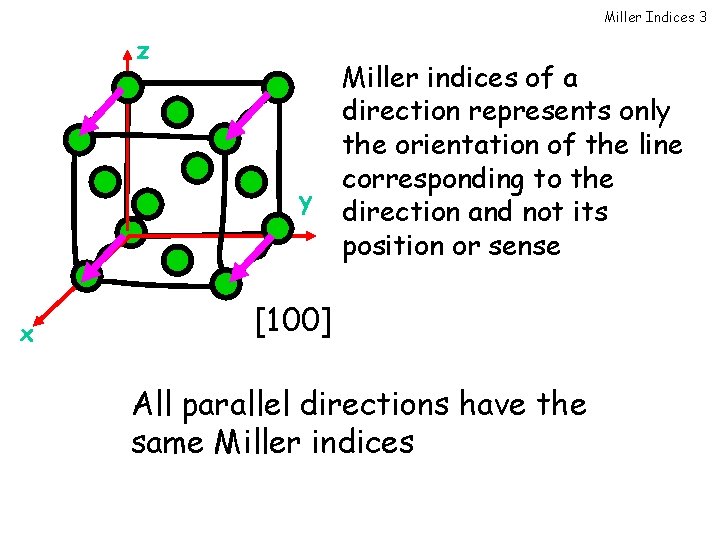
Miller Indices 3 z y x Miller indices of a direction represents only the orientation of the line corresponding to the direction and not its position or sense [100] All parallel directions have the same Miller indices

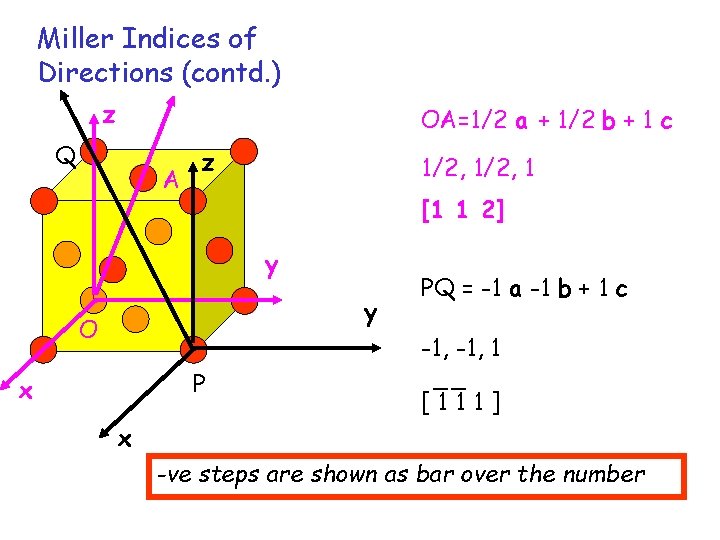
Miller Indices of Directions (contd. ) z OA=1/2 a + 1/2 b + 1 c Q A z 1/2, 1 [1 1 2] y y O P x PQ = -1 a -1 b + 1 c -1, 1 __ [111] x -ve steps are shown as bar over the number

Miller Indices 4 Miller indices of a family of symmetry related directions = [uvw] and all other directions related to [uvw] by the symmetry of the crystal [001] Tetragonal Cubic [010] [100] = [100], [010], [001] [100] = [100], [010]

End of Lec 05 31/07/2013 Lec 3 on crystallography

Lec 6 Lec 4 on crystallography Miller Indices Continues

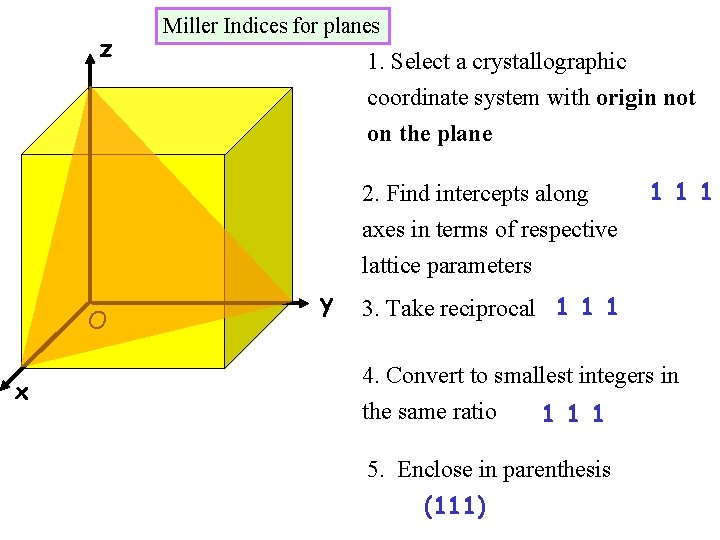
z Miller Indices for planes 1. Select a crystallographic coordinate system with origin not on the plane 2. Find intercepts along 1 1 1 axes in terms of respective lattice parameters O x y 3. Take reciprocal 1 1 1 4. Convert to smallest integers in the same ratio 1 1 1 5. Enclose in parenthesis (111)

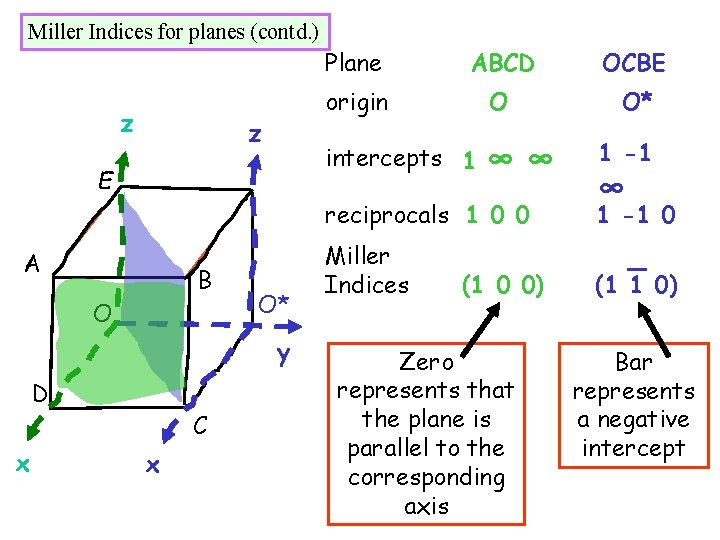
Miller Indices for planes (contd. ) z z E Plane ABCD OCBE origin O O* intercepts 1 ∞ ∞ reciprocals 1 0 0 A B O O* y D x C x Miller Indices (1 0 0) Zero represents that the plane is parallel to the corresponding axis 1 -1 ∞ 1 -1 0 _ (1 1 0) Bar represents a negative intercept

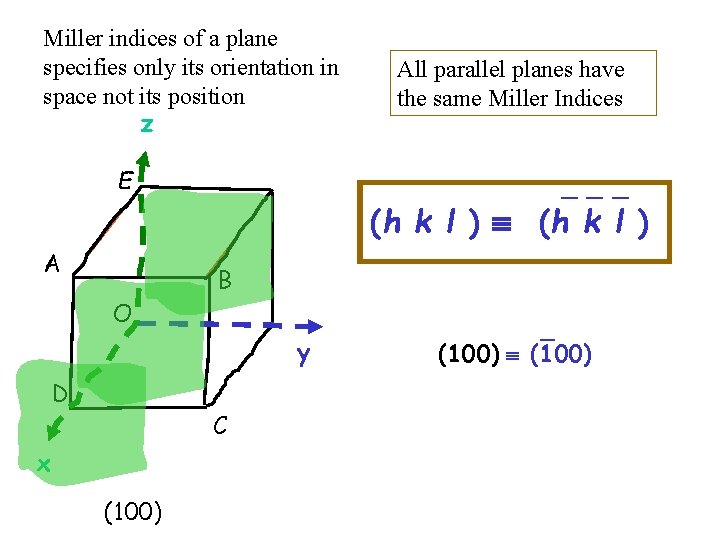
Miller indices of a plane specifies only its orientation in space not its position z E All parallel planes have the same Miller Indices _ _ _ (h k l ) A B O y D C x (100) _ (100)

Z Y X

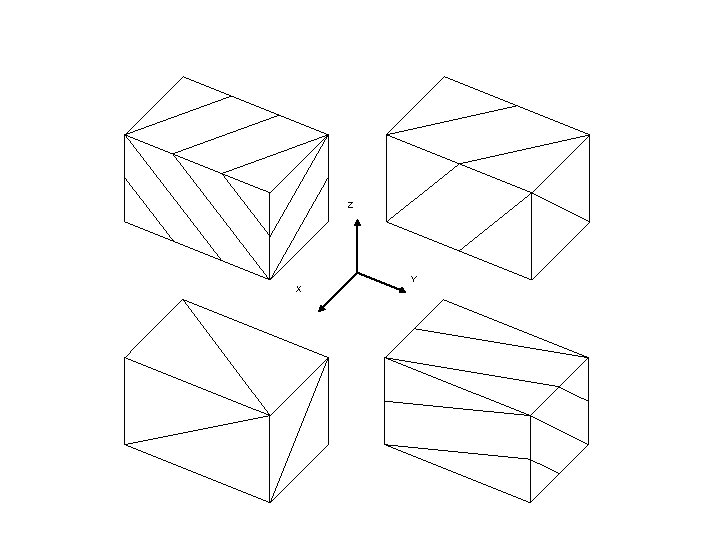
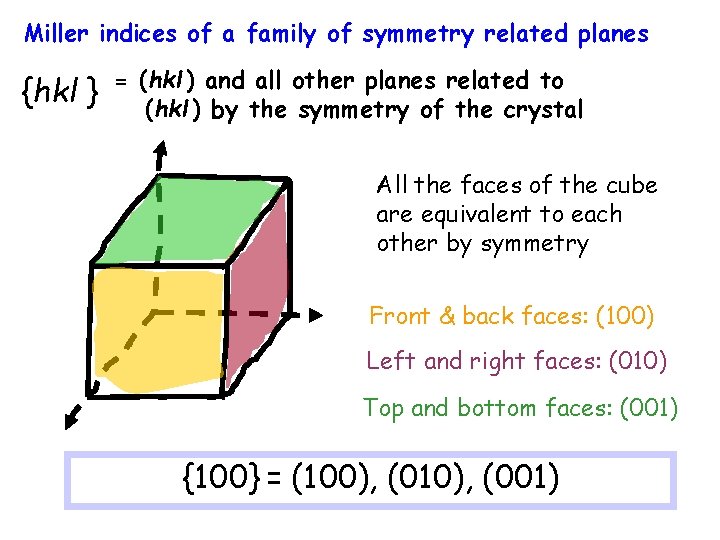
Miller indices of a family of symmetry related planes {hkl } = (hkl ) and all other planes related to (hkl ) by the symmetry of the crystal All the faces of the cube are equivalent to each other by symmetry Front & back faces: (100) Left and right faces: (010) Top and bottom faces: (001) {100} = (100), (010), (001)

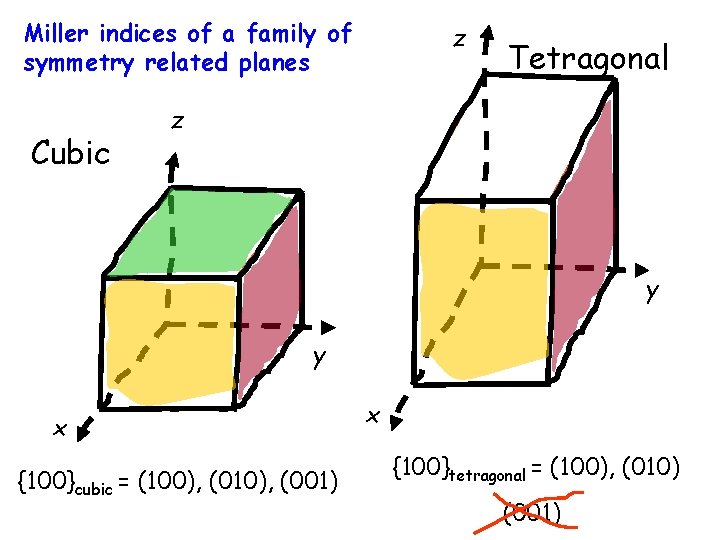
Miller indices of a family of symmetry related planes Cubic z Tetragonal z y y x {100}cubic = (100), (010), (001) x {100}tetragonal = (100), (010) (001)

Some IMPORTANT Results Weiss zone law Not in the textbook Condition for a direction [uvw] to be parallel to a plane or lie in the plane (hkl): hu+kv+lw=0 True for ALL crystal systems

CUBIC CRYSTALS [111] [hkl] (hkl) (111) Angle between two directions [h 1 k 1 l 1] and [h 2 k 2 l 2]: C

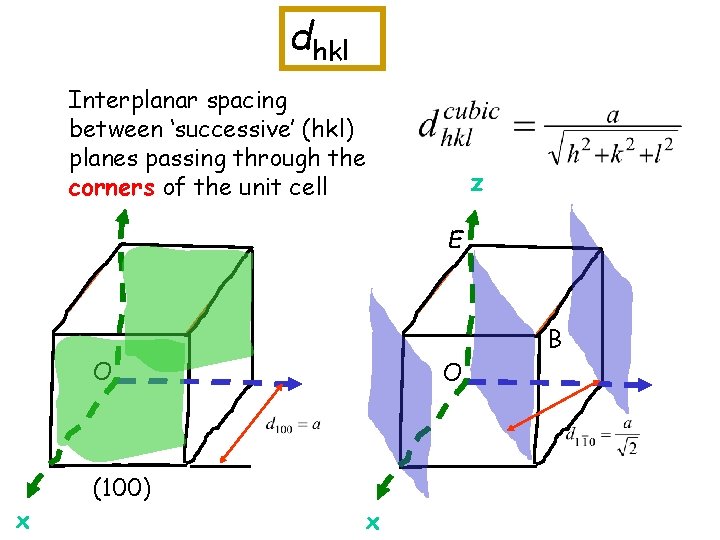
dhkl Interplanar spacing between ‘successive’ (hkl) planes passing through the corners of the unit cell z E B O x (100) O x

Summary of Notation convention for Indices [uvw] Miller indices of a direction (i. e. a set of parallel directions) (hkl) Miller Indices of a plane (i. e. a set of parallel planes) <uvw> Miller indices of a family of symmetry related directions {hkl} Miller indices of a family of symmetry related planes

In the fell clutch of circumstance I have not winced nor cried aloud. Under the bludgeonings of chance My head is bloody, but unbowed. From "Invictus" by William Ernest Henley (1849– 1903).

End of Lecture 6 Lec 4 on crystallography

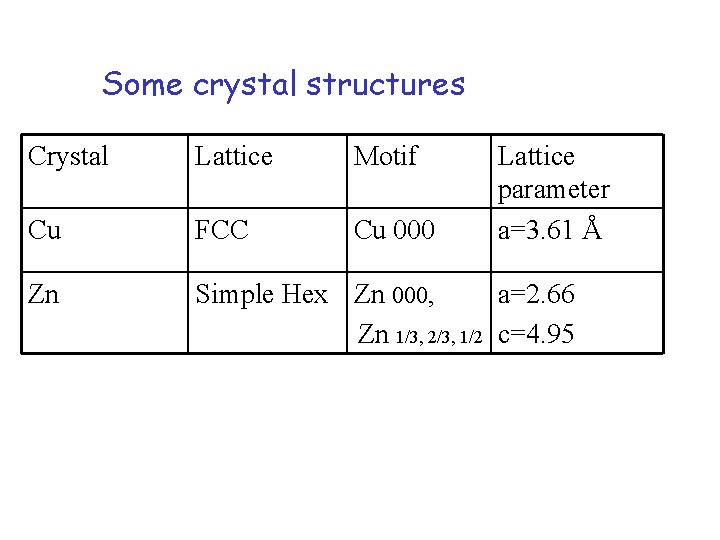
Some crystal structures Crystal Lattice Motif Lattice parameter a=3. 61 Å Cu FCC Cu 000 Zn Simple Hex Zn 000, a=2. 66 Zn 1/3, 2/3, 1/2 c=4. 95

Q 1: How do we determine the crystal structure?

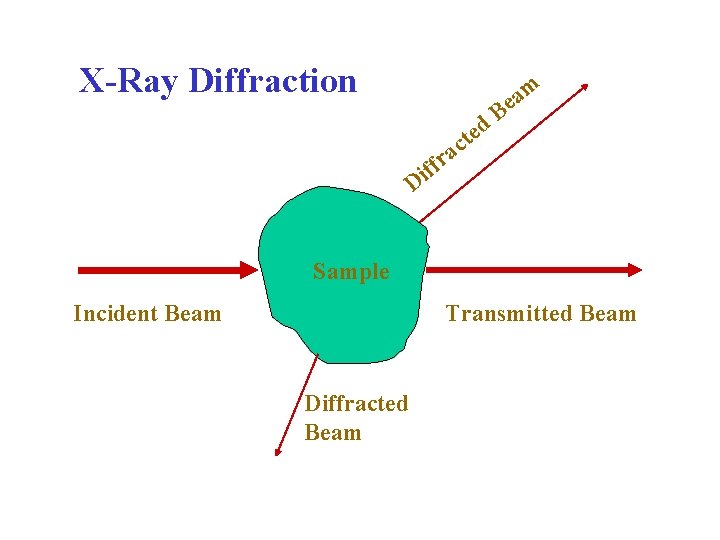
X-Ray Diffraction d e t c am e B a r f if D Sample Incident Beam Transmitted Beam Diffracted Beam

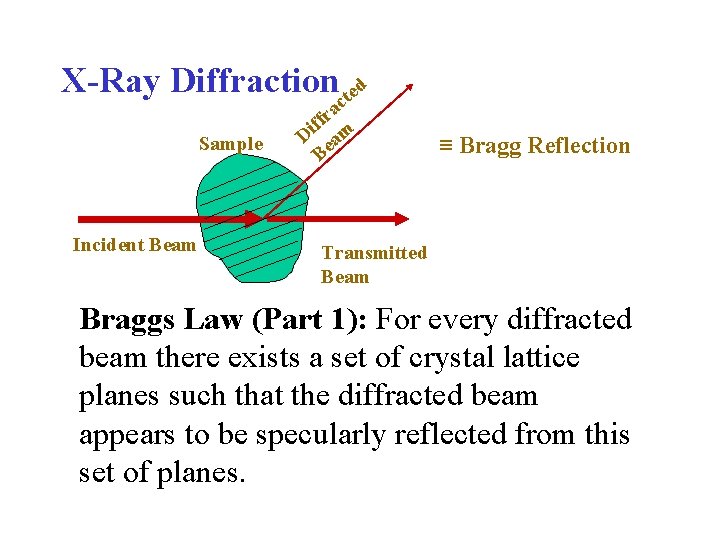
X-Ray Diffraction cted Sample Incident Beam a r f f m i D ea B ≡ Bragg Reflection Transmitted Beam Braggs Law (Part 1): For every diffracted beam there exists a set of crystal lattice planes such that the diffracted beam appears to be specularly reflected from this set of planes.

X-Ray Diffraction Braggs’ recipe for Nobel prize? Call the diffraction a reflection!!! “The important thing in science is not so much to obtain new facts as to discover new ways of thinking about them”. W. L. Bragg

X-Ray Diffraction Braggs Law (Part 1): the diffracted beam appears to be specularly reflected from a set of crystal lattice planes. Specular reflection: Angle of incidence i =Angle of reflection (both measured from the plane and not from the normal) r The incident beam, the reflected beam and the plane normal lie in one plane

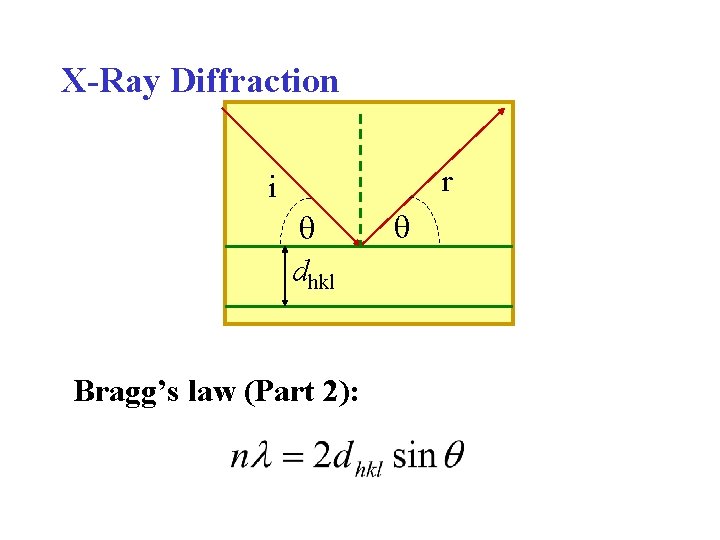
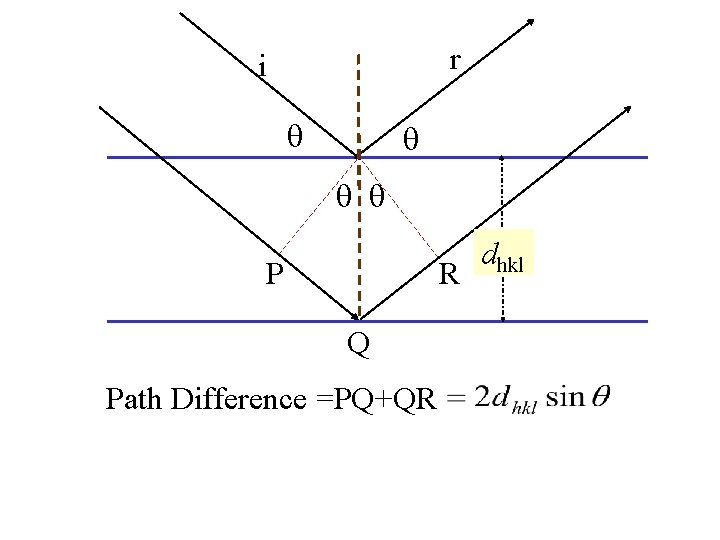
X-Ray Diffraction r i dhkl Bragg’s law (Part 2):

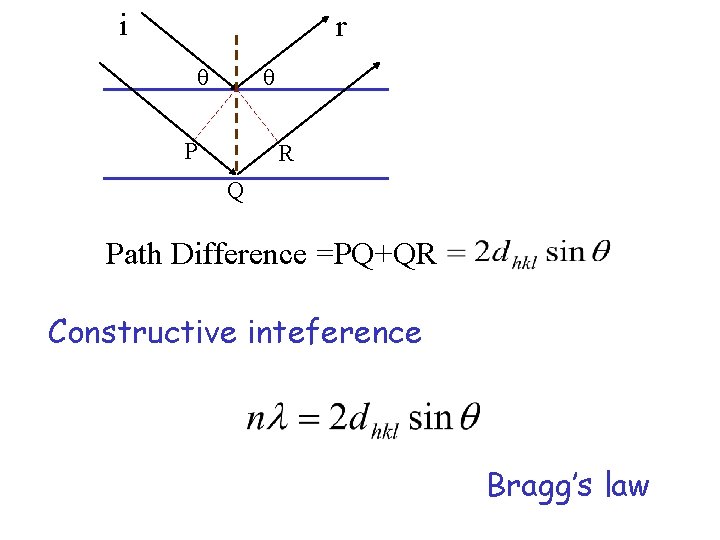
r i P R Q Path Difference =PQ+QR dhkl

i r P R Q Path Difference =PQ+QR Constructive inteference Bragg’s law

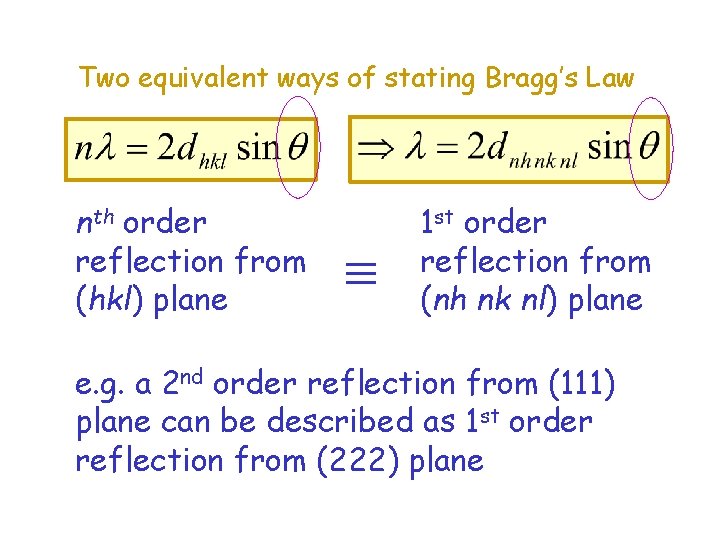
Two equivalent ways of stating Bragg’s Law 1 st Form 2 nd Form

Two equivalent ways of stating Bragg’s Law nth order reflection from (hkl) plane 1 st order reflection from (nh nk nl) plane e. g. a 2 nd order reflection from (111) plane can be described as 1 st order reflection from (222) plane

X-rays Characteristic Radiation, K Target Mo Cu Co Fe Cr Wavelength, Å 0. 71 1. 54 1. 79 1. 94 2. 29

Powder Method is fixed (K radiation) is variable – specimen consists of millions of powder particles – each being a crystallite and these are randomly oriented in space – amounting to the rotation of a crystal about all possible axes

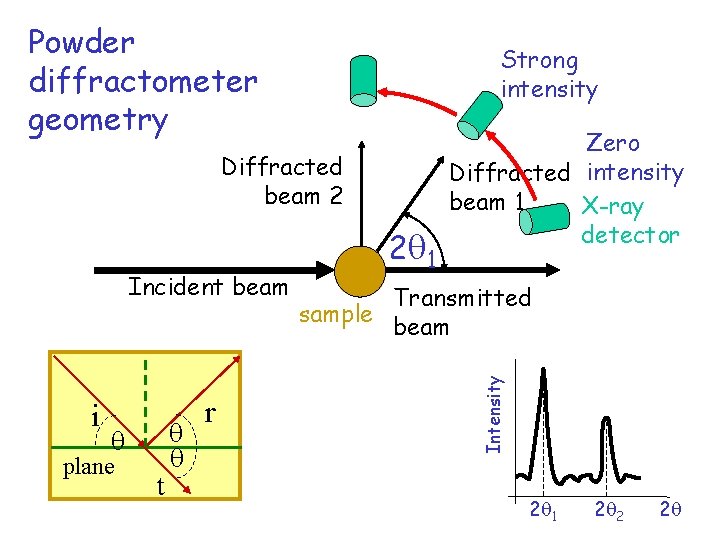
Powder diffractometer geometry Strong intensity Diffracted beam 2 i plane t r Transmitted sample beam Intensity Incident beam 2 1 Zero Diffracted intensity beam 1 X-ray detector 2 1 2 2 2

Crystal monochromator detector X-ray tube X-ray powder diffractometer

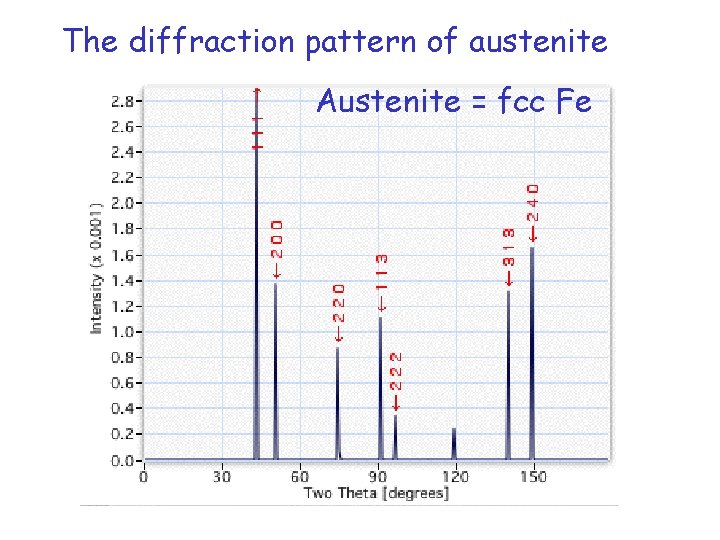
The diffraction pattern of austenite Austenite = fcc Fe

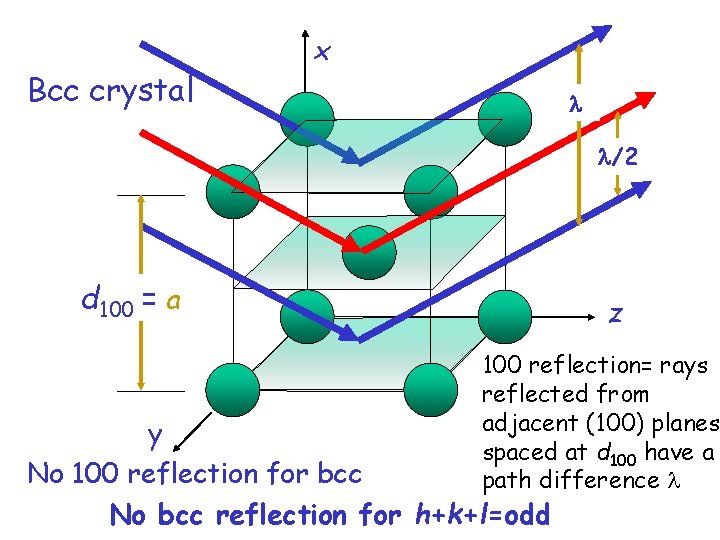
Bcc crystal x /2 d 100 = a z 100 reflection= rays reflected from adjacent (100) planes spaced at d 100 have a path difference y No 100 reflection for bcc No bcc reflection for h+k+l=odd

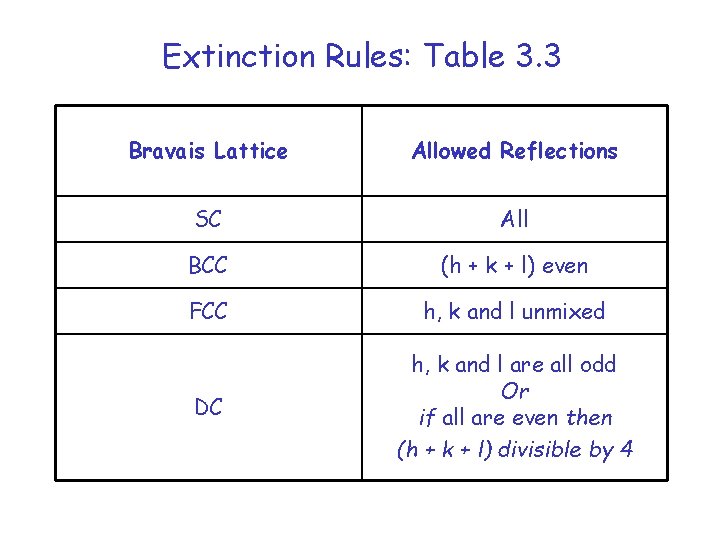
Extinction Rules: Table 3. 3 Bravais Lattice Allowed Reflections SC All BCC (h + k + l) even FCC h, k and l unmixed DC h, k and l are all odd Or if all are even then (h + k + l) divisible by 4

End of Lec 7 06/08/13 Lec 5 on crystallography (Last lecture)

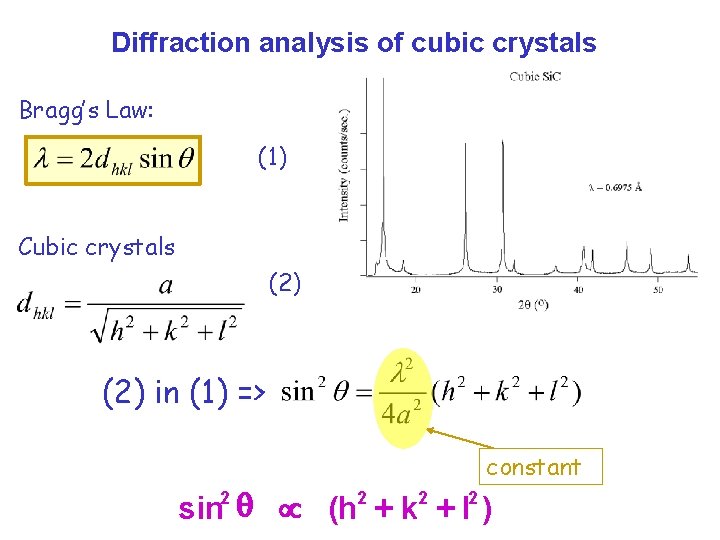
Diffraction analysis of cubic crystals Bragg’s Law: (1) Cubic crystals (2) in (1) => constant sin q µ (h + k + l ) 2 2

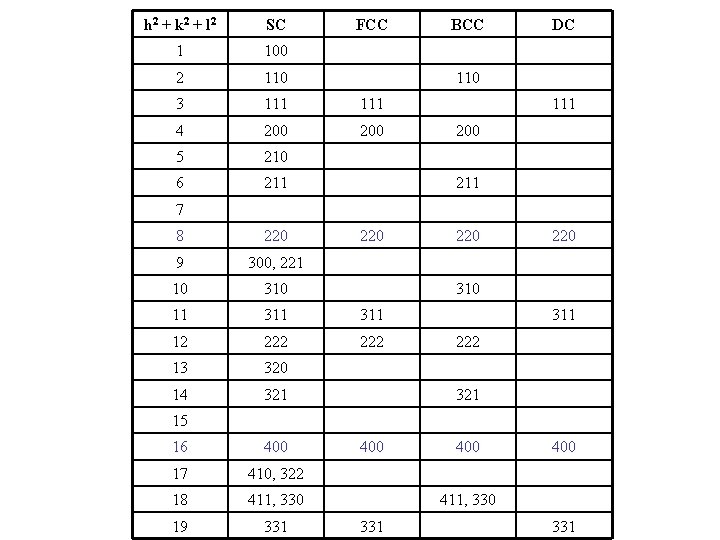
h 2 + k 2 + l 2 SC FCC 1 100 2 110 3 111 4 200 5 210 6 211 BCC DC 110 111 200 211 7 8 220 9 300, 221 10 310 11 311 12 222 13 320 14 321 220 310 311 222 321 15 16 400 17 410, 322 18 411, 330 19 331 400 400 411, 330 331

Crystal Structure Allowed ratios of Sin 2 (theta) SC 1: 2: 3: 4: 5: 6: 8: 9… BCC 1: 2: 3: 4: 5: 6: 7: 8… FCC 3: 4: 8: 11: 12… DC 3: 8: 11: 16…

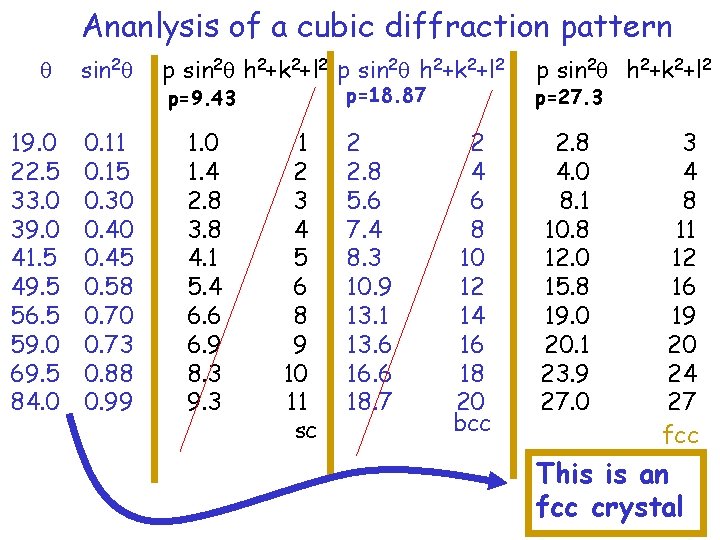
Ananlysis of a cubic diffraction pattern 19. 0 22. 5 33. 0 39. 0 41. 5 49. 5 56. 5 59. 0 69. 5 84. 0 sin 2 0. 11 0. 15 0. 30 0. 45 0. 58 0. 70 0. 73 0. 88 0. 99 p sin 2 h 2+k 2+l 2 p=18. 87 p=9. 43 1. 0 1. 4 2. 8 3. 8 4. 1 5. 4 6. 6 6. 9 8. 3 9. 3 1 2 3 4 5 6 8 9 10 11 sc 2 2. 8 5. 6 7. 4 8. 3 10. 9 13. 1 13. 6 16. 6 18. 7 2 4 6 8 10 12 14 16 18 20 bcc p sin 2 h 2+k 2+l 2 p=27. 3 2. 8 4. 0 8. 1 10. 8 12. 0 15. 8 19. 0 20. 1 23. 9 27. 0 3 4 8 11 12 16 19 20 24 27 fcc This is an fcc crystal

Ananlysis of a cubic diffraction pattern contd. 19. 0 22. 5 33. 0 39. 0 41. 5 49. 5 56. 5 59. 0 69. 5 84. 0 h 2+k 2+l 2 3 4 8 11 12 16 19 20 24 27 hkl a 111 200 220 311 222 400 331 420 422 511 4. 05 4. 02 4. 04 4. 03 4. 04 4. 01 4. 03 Indexing of diffraction patterns 2 4 a (h + k + l ) = 2 sin 2 2 The diffraction pattern is from an fcc crystal of lattice parameter 4. 03 Å

Education is an admirable thing, but it is well to remember from time to time that nothing that is worth knowing can be taught. -Oscar Wilde

A father-son team that shared a Nobel Prize William Henry Bragg (1862– 1942), William Lawrence Bragg (1890– 1971) Nobel Prize (1915)

One of the greatest scientific discoveries of twentieth century

Max von Laue, 1879 -1960 Nobel 1914

Two Questions Q 1: X-rays waves or particles? Father Bragg: Particles Son Bragg: Waves “Even after they shared a Nobel Prize in 1915, … this tension persisted…” – Ioan James in Remarkable Physicists Q 2: Crystals: Perodic arrangement of atoms? X-RAY DIFFRACTION: X-rays are waves and crystals are periodic arrangement of atoms

If it is permissible to evaluate a human discovery according to the fruits which it bears then there are not many discoveries ranking on par with that made by von Laue. -from Nobel Presentation Talk

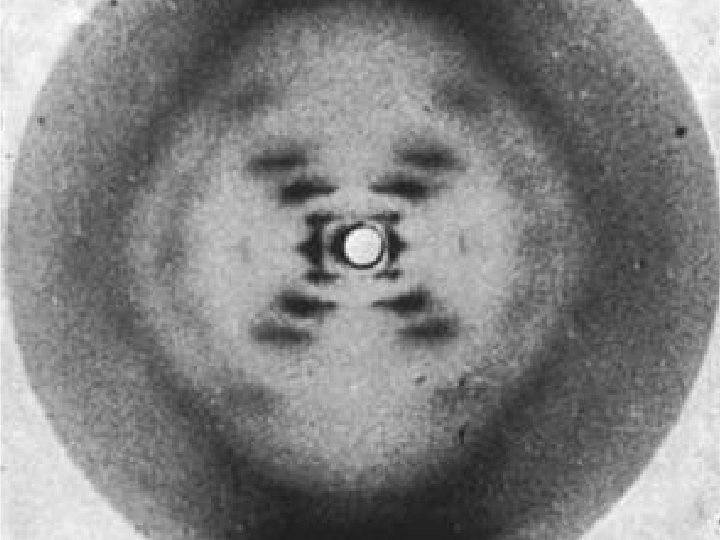
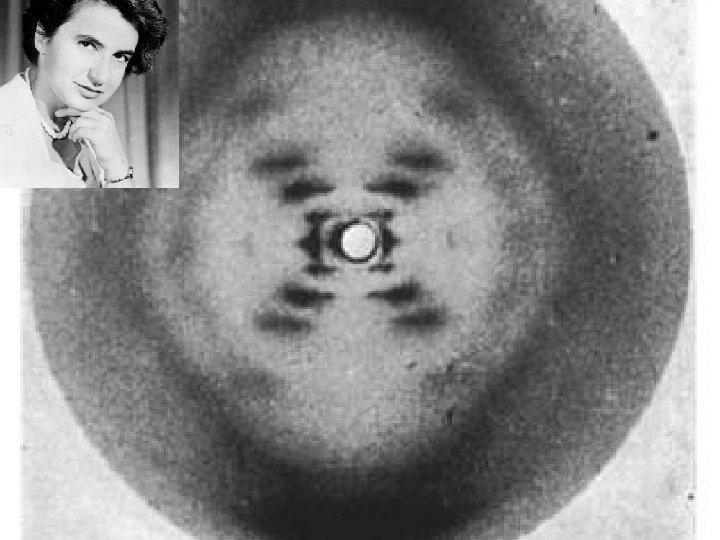
Watson, Crick and Wilkins Nobel Prize, 1962

Rosalind Elsie Franklin

Rosy, of course, did not directly give us her data. For that matter, no one at King's realized they were in our hands. J. D. Watson "However, the data which really helped us to obtain the structure was mainly obtained by Rosalind Franklin". -Francis Crick

Google Doodle on 25 th July, 2013 Franklins birth centenary 25 July 2020

Rosalind Elsie Franklin 25 July 1920 – 16 April 1958