Teoria wzgldnoci Szczeglna teoria wzgldnoci Transformacje Galileusza Przyspieszenie












































- Slides: 62

Teoria względności Szczególna teoria względności

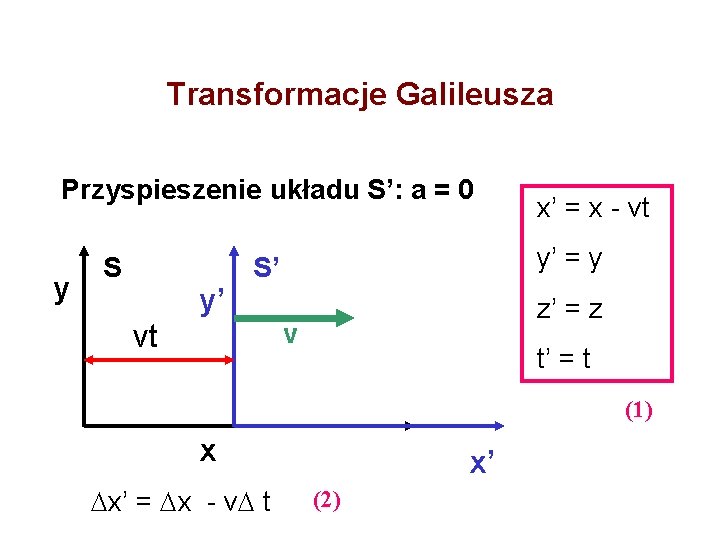
Transformacje Galileusza Przyspieszenie układu S’: a = 0 y S y’ y’ = y S’ z’ = z v vt x’ = x - vt t’ = t (1) x x’ = x - v t x’ (2)

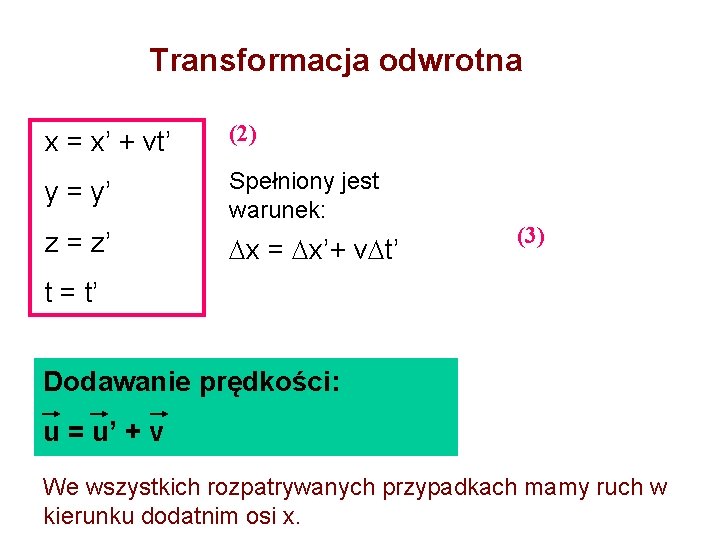
Transformacja odwrotna x = x’ + vt’ (2) y = y’ Spełniony jest warunek: z = z’ x = x’+ v t’ (3) t = t’ Dodawanie prędkości: u = u’ + v We wszystkich rozpatrywanych przypadkach mamy ruch w kierunku dodatnim osi x.

Einstein oparł swoją teorię na dwóch postulatach: 1) zwany zasadą względności, 2) dotyczący stałości prędkości światła we wszystkich układach inercjalnych. Ad 1) Od czasów Galileusza wiedziano, że prawa mechaniki (fizyki) są takie same we wszystkich układach inercjalnych. Einstein rozszerzył ten pogląd na obszar całej fizyki, a w szczególności elektromagnetyzmu. Ad 2) Drugi postulat natomiast oznaczał, że hipotetyczny eter nie jest potrzebny do propagacji fal elektromagnetycznych. Wszystkie wnioski dotyczące szczególnej teorii

1. Zasada względności We wszystkich układach inercjalnych prawa fizyki są jednakowe. Układ odniesienia, w którym ciało nie poddane działaniu sił pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym nazywamy układem inercjalnym. Każdy układ poruszający się względem układu inercjalnego ruchem jednostajnym jest też układem inercjalnym.

Ziemia widziana z Księżyca

2. Postulat szczególnej teorii względności Prędkość światła nie zależy od układu odniesienia. Przed ogłoszeniem przez Einsteina teorii względności Michelson i Morley wykonali pomiary prędkości światła polegające na porównaniu rozchodzenia się prędkości dwóch wiązek świetlnych w próżni, z których jedna poruszała się w kierunku północ południe, druga w kierunku wschód - zachód. Należało oczekiwać, że prędkości tych wiązek będą różne. Doświadczenie pokazało, że w próżni światło porusza się z prędkością c, niezależnie od ruchu źródła lub obserwatora.

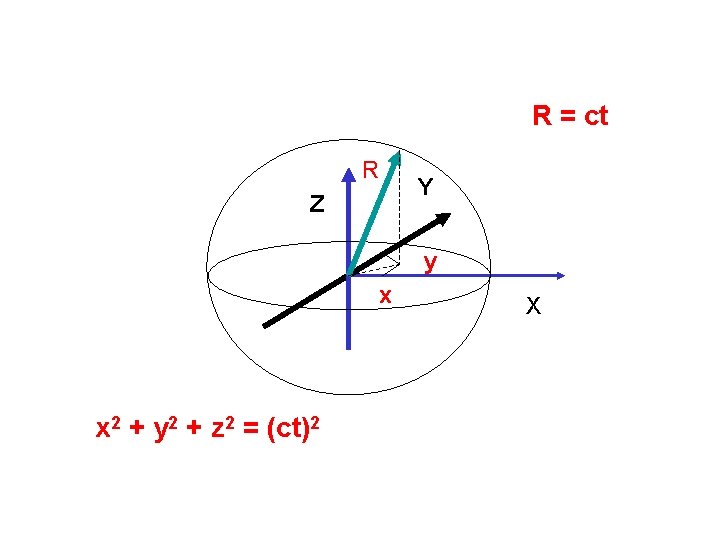
Transformacja relatywistyczna Dodawanie prędkości: c=c+v c=c-v W przypadku kulistej fali światła w układzie S: w układzie S’: x 2 + y 2 + z 2 = c 2 t 2 (4) x’ 2 + y’ 2 + z’ 2 = c 2 t’ 2 (5) W kinematyce nierelatywistycznej obowiązywało: x’ = x - vt t = t’

R = ct R Z Y y x x 2 + y 2 + z 2 = (ct)2 X

Natomiast w przypadku kinematyki relatywistycznej wprowadzono współczynnik x’ = (x - vt) x = ’(x’ + vt’) (6) Skoro nie istnieje wyróżniony układ współrzędnych inercjalnych, to ’ = (6 a) Szukamy transformacji czasu x = (x’ + vt’) x - x’ = vt’ ale x’ = (x - vt) czyli (7)

Z (1) wynika, że y’ = y z’ = z (8) (9) Po uporządkowaniu (10) Szukamy takiego , aby (10) było identyczne z (4) x 2 + y 2 + z 2 = c 2 t 2

Zatem musi być c 2 2 - v 2 2 = c 2 z tego warunku wynika, że (11)

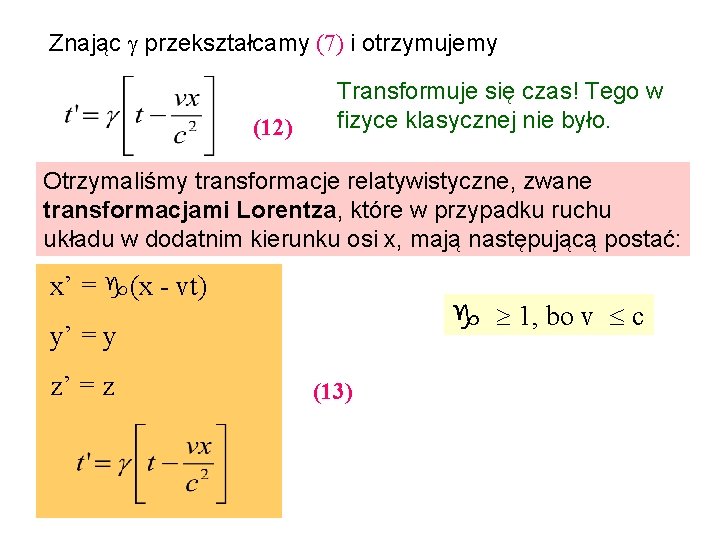
Znając przekształcamy (7) i otrzymujemy (12) Transformuje się czas! Tego w fizyce klasycznej nie było. Otrzymaliśmy transformacje relatywistyczne, zwane transformacjami Lorentza, które w przypadku ruchu układu w dodatnim kierunku osi x, mają następującą postać: x’ = (x - vt) 1, bo v c y’ = y z’ = z (13)

(14) Transformacje odwrotne mają postać następującą: x = (x’ + vt’) y = y’ z = z’ (15)

Równoczesność zdarzeń • • • A 0 B Punkt 0 leży w połowie odległości między punktami A i B. Z punktu 0 emitowana jest kulista fala świetlna. Zdarzenia polegające na tym, że do punktów A i B dociera światło jednocześnie są równoczesne, ponieważ jest taka sama droga światła.

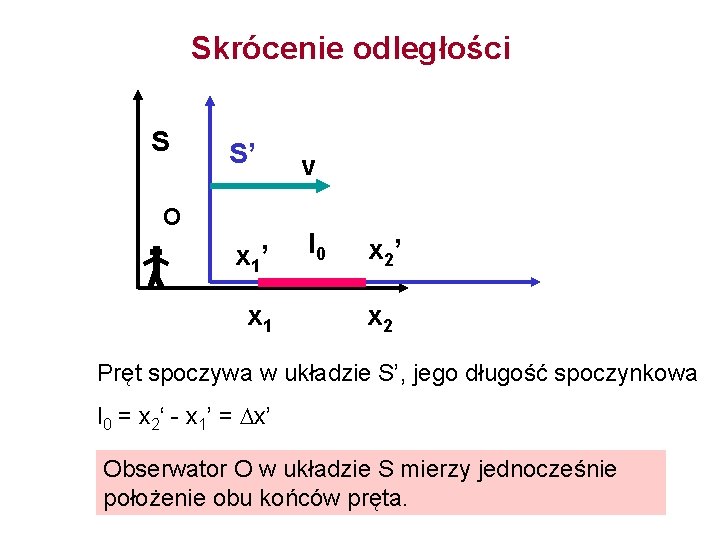
Skrócenie odległości S S’ v x 1’ l 0 O x 1 x 2’ x 2 Pręt spoczywa w układzie S’, jego długość spoczynkowa l 0 = x 2‘ - x 1’ = x’ Obserwator O w układzie S mierzy jednocześnie położenie obu końców pręta.

x 2‘ - x 1’ = (x 2 - vt) - (x 1 - vt) = (x 2 - x 1) x’ = x 1 x < x’ Długość L mierzona przez obserwatora O w układzie S jest mniejsza niż zmierzona w układzie S’. (16) Skróceniu ulegają tylko wymiary równoległe do wektora prędkości v.

Stanfordt (w pobliżu San Francisco). Akcelerator liniowy LINAC o długości 3 km, dwie wiązki przeciwbieżne elektronów i pozytonów, uzyskuje się energię rzędu Ge. V. pl. wikipedia. org/wiki/

Dylatacja czasu. Paradoks bliźniąt. Zegar spoczywa w początku układu S. Mierzy odstęp czasu t między zjawiskami, które zaszły w tym samym punkcie układu S’ np. x’, (t 1’, t 2’). (17) Wskazania zegara w układzie S są większe od wskazań w układzie S’.

Dwa obiekty mijają się w chwili jednakowych wskazań zegarów

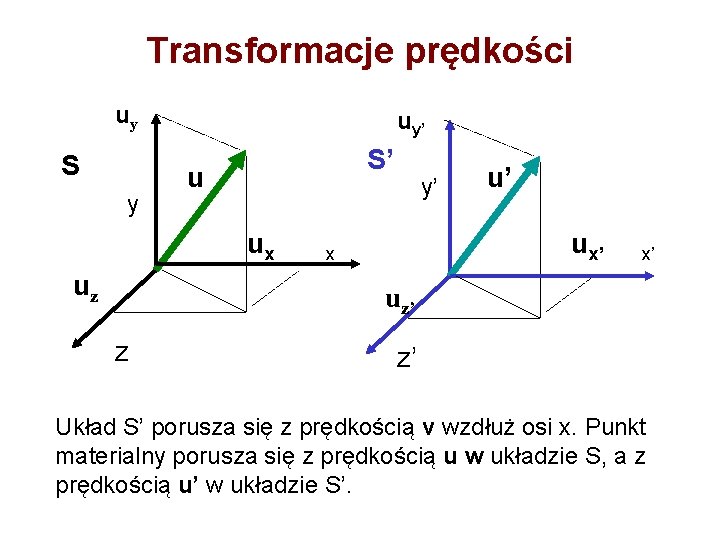
Transformacje prędkości uy S y uy’ S’ u ux uz y’ u’ ux’ x x’ uz’ z z’ Układ S’ porusza się z prędkością v wzdłuż osi x. Punkt materialny porusza się z prędkością u w układzie S, a z prędkością u’ w układzie S’.

x’ = (x - vt) dx’ = (dx – vdt) y’ = y dy’ = dy z’ = z dz’ = dz Obliczamy składowe prędkości w układzie S’. (18)

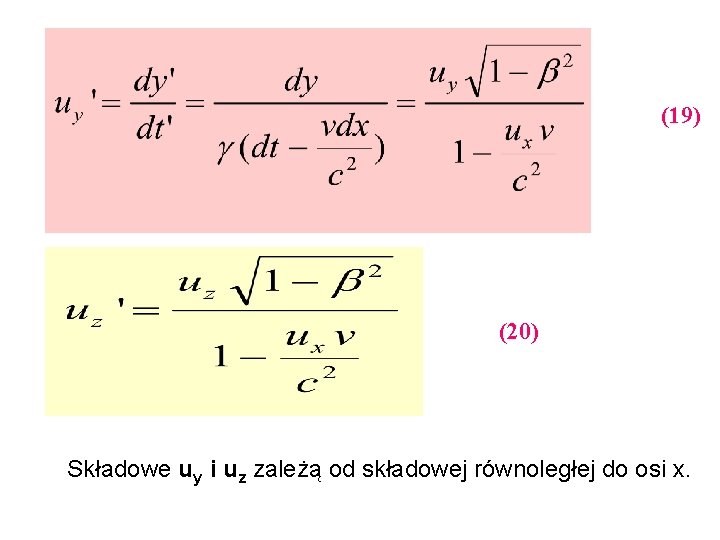
(19) (20) Składowe uy i uz zależą od składowej równoległej do osi x.

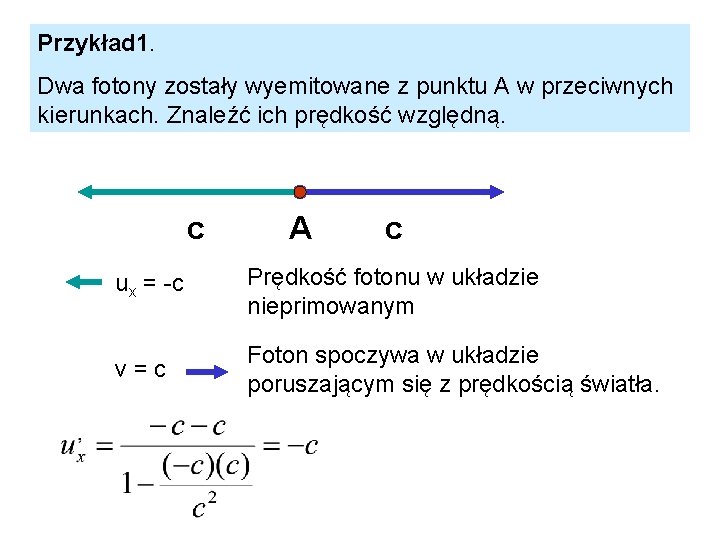
Przykład 1. Dwa fotony zostały wyemitowane z punktu A w przeciwnych kierunkach. Znaleźć ich prędkość względną. c A c ux = -c Prędkość fotonu w układzie nieprimowanym v=c Foton spoczywa w układzie poruszającym się z prędkością światła.

Interwał czasoprzestrzenny S 2 = c 2(t 2 - t 1)2 - (x 2 -x 1)2 - (y 2 - y 1)2 -(z 2 - z 1)2 (21) S’ 2 = c 2(t’ 2 - t’ 1)2 - (x’ 2 -x’ 1)2 - (y’ 2 - y’ 1)2 -(z’ 2 - z’ 1)2 S’ 2 = S 2 (23) (22) Interwał między zdarzeniami 1 i 2 jest niezmienniczy względem transformacji Lorentza. W zakresie szczególnej teorii względności x = x’ i y = y’, więc słuszny jest związek: ( s)2 = (c t)2 - ( x)2 = (c t’)2 - ( x’)2 (24)

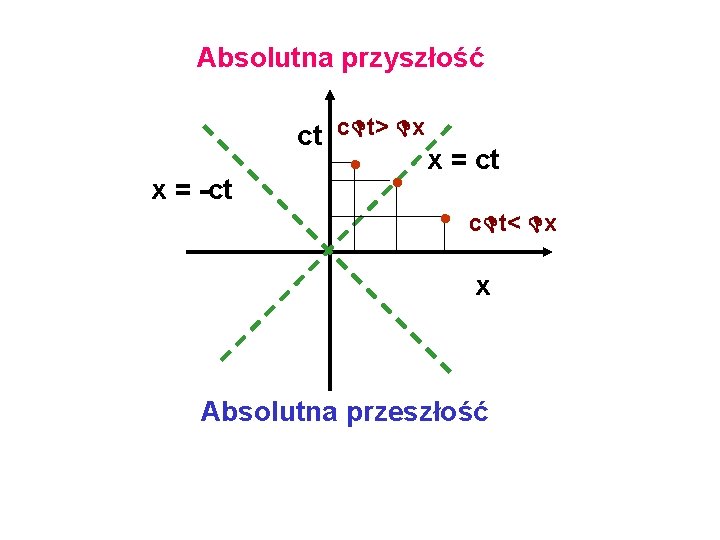
Absolutna przyszłość ct c t> x x = -ct • x = ct • c t< x x Absolutna przeszłość

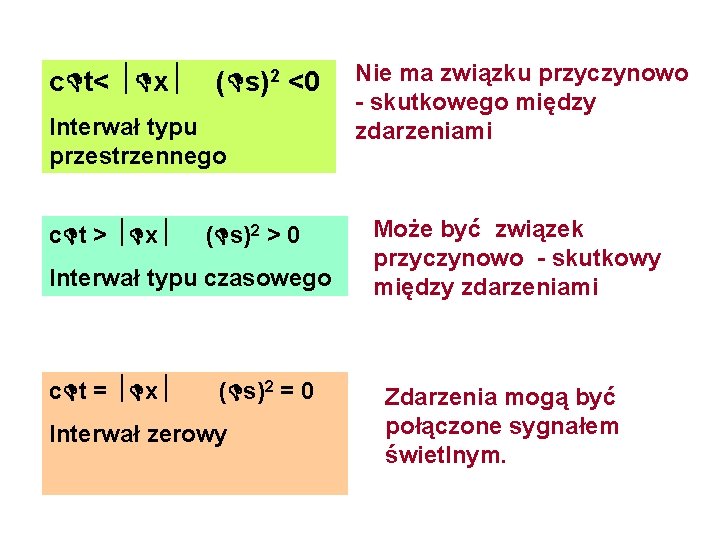
c t< x ( s)2 <0 Interwał typu przestrzennego c t > x ( s)2 > 0 Interwał typu czasowego c t = x ( s)2 = 0 Interwał zerowy Nie ma związku przyczynowo - skutkowego między zdarzeniami Może być związek przyczynowo - skutkowy między zdarzeniami Zdarzenia mogą być połączone sygnałem świetlnym.

Dynamika relatywistyczna Pęd i energia p = M 0 v (25) E = M 0 c 2 (26)

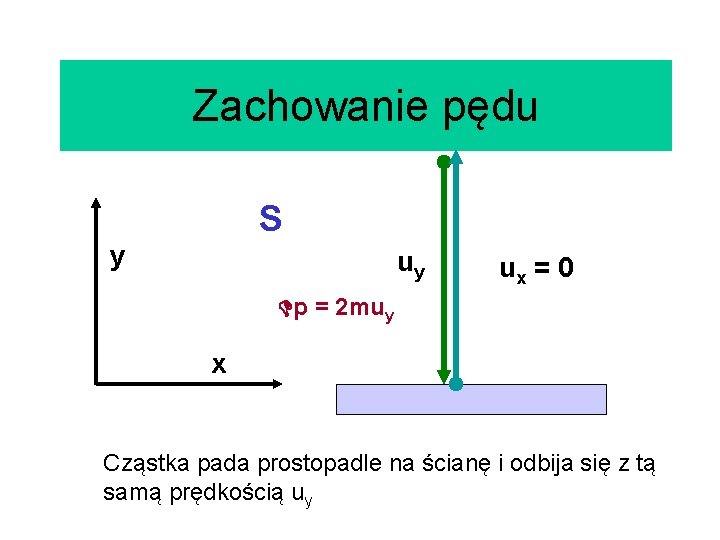
Zachowanie pędu S y uy ux = 0 p = 2 muy x Cząstka pada prostopadle na ścianę i odbija się z tą samą prędkością uy

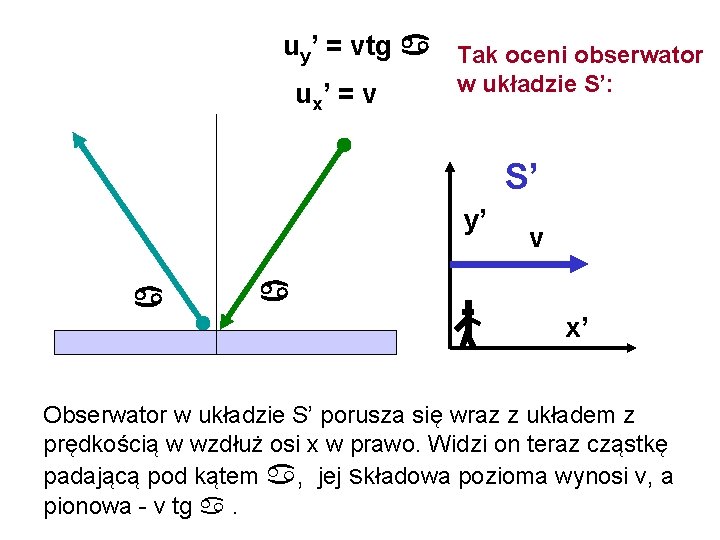
uy’ = vtg Tak oceni obserwator w układzie S’: u x’ = v S’ y’ v x’ Obserwator w układzie S’ porusza się wraz z układem z prędkością w wzdłuż osi x w prawo. Widzi on teraz cząstkę padającą pod kątem , jej składowa pozioma wynosi v, a pionowa - v tg .

Wstawiając ux = 0 otrzymujemy ux’ = - v uy’ = v tg py’= 2 muy’ Wartości składowych prędkości w układach S i S’ nie są sobie równe, jak również nie są równe składowe pędu cząstki. Widzimy, że określenie pędu jako wielkości proporcjonalnej do prędkości nie wystarcza do utrzymania zasady zachowania pędu we wszystkich układach odniesienia.

Jeżeli zdefiniujemy pęd relatywistyczny cząstki o masie spoczynkowej M 0 jako (25 a) to zasada zachowania pędu jest słuszna w każdym innym układzie inercjalnym, który różni się od układu pozostającego w spoczynku stałą prędkością v poruszania się w kierunku osi x. Na tej podstawie wyrażenie: (27) . (

(27 a) M(v) interpretujemy jako relatywistyczną masę Masa spoczynkowa M 0 jest to masa M(v) dla v 0. Gdy v c M(v) .

Relatywistyczna II zasada dynamiki Newtona Siłę F działającą na ciało o masie spoczynkowej Mo obliczamy na podstawie pędu relatywistycznego, ponieważ druga zasada zdefiniowana jest tym samym wzorem co w mechanice klasycznej: (28) Stąd dla przypadku ruchu w jednym kierunku (29)

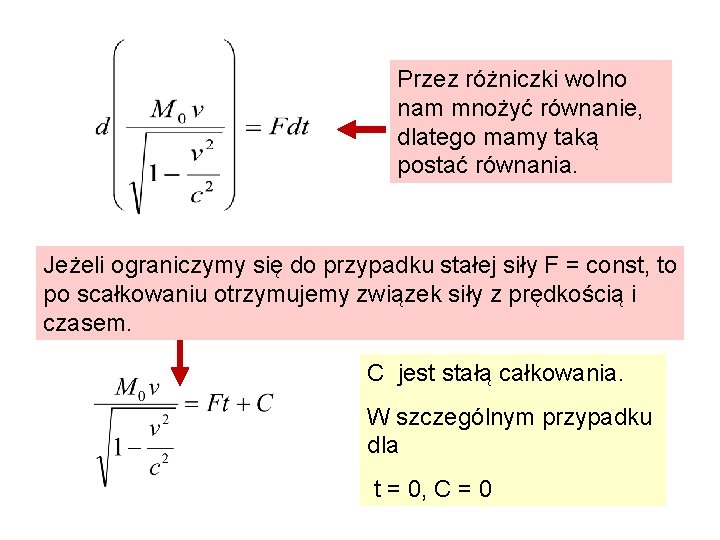
Przez różniczki wolno nam mnożyć równanie, dlatego mamy taką postać równania. Jeżeli ograniczymy się do przypadku stałej siły F = const, to po scałkowaniu otrzymujemy związek siły z prędkością i czasem. C jest stałą całkowania. W szczególnym przypadku dla t = 0, C = 0

Klasyczny związek energii z pędem Pęd : gdzie: m – masa, v – prędkość cząstki materialnej Energia kinetyczna: Związek energii kinetycznej z pędem:

Energia relatywistyczna, związek energii z pędem Zgodnie z wzorem (25), kwadrat pędu można zapisać w postaci: (30) Tożsamość (31) lub (31 a) jest niezmiennikiem Lorentza, bo 1 jest stałą. Mnożąc obie strony równania (31 a) przez

otrzymamy (32) lub (33) Wyrażenie to jest stałe, ponieważ masa spoczynkowa jest stała i tym samym jest niezmiennicze wobec transformacji Lorentza. Wszystkie wyrazy wzoru (33) mają wymiar kwadratu energii, stąd następująca definicja całkowitej energii cząstki (26 a)

Przy tak zdefiniowanej energii otrzymujemy relatywistyczny związek pędu z energią całkowitą E i energią spoczynkową M 0 c 2 o postaci: (34) Wyrażenie Ek = 1/2 Mv 2 opisujące klasyczną energię kinetyczną jest niesłuszne w zakresie prędkości bliskich prędkości światła c. Energię kinetyczną obliczamy teraz jako Ek = E - E 0 = E - M 0 c 2 (35) gdzie E jest zdefiniowana przez (26).

Można jednak pokazać, że przy małych wartościach prędkościach v wzór relatywistyczny (33) jest zgodny z klasycznym wyrażeniem na energię kinetyczną Ek = 1/2 Mv 2. W tym celu skorzystamy z rozwinięcia w szereg dwumianu. W naszym przypadku n = -1/2, x = - (v/c)2. Zatem Jeżeli v << c, to można opuścić wyrazy o wyższych potęgach i otrzymamy klasyczny wzór na energię kinetyczną.

Równoważność masy i energii Możliwość przemiany masy spoczynkowej na energię i związek ilościowy między tymi wielkościami była według Einsteina najważniejszym wynikiem uzyskanym w teorii względności. Z wzoru (26) wynika, że można napisać: E = M(v)c 2 (26 b) oraz że zmiana energii E = 2 Mc (36)

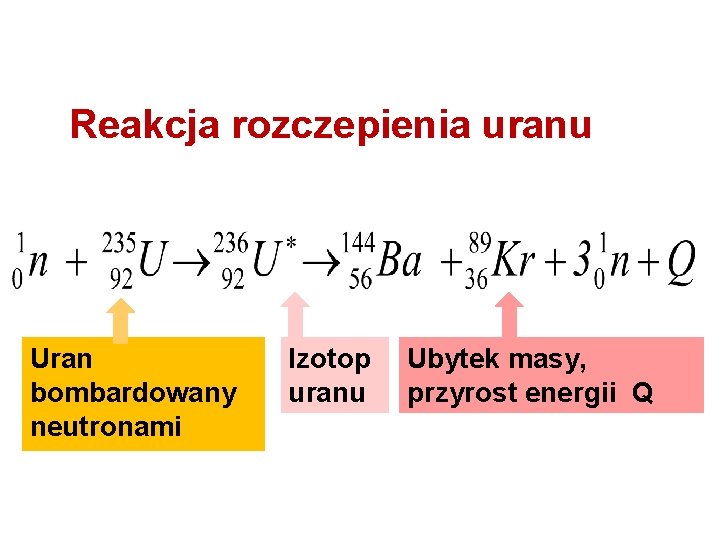
Reakcja rozczepienia uranu Uran bombardowany neutronami Izotop uranu Ubytek masy, przyrost energii Q

Przykład 2. Jakiej masie równoważna jest energia wysyłana przez antenę radiową o mocy 1 k. W w ciągu doby? 1 doba = 86400 s E = 86400000 J = 8. 64 • 107 J

Pęd kwantu Jeżeli do wzoru wstawimy M 0 = 0, otrzymamy E = pc p pęd cząstki o zerowej masie spoczynkowej (kwant) (37)

Foton ma zerową masę spoczynkową, warunkiem istnienia fotonu jest energia i pęd. Dzięki równoważności masy i energii można mu przypisać masę relatywistyczną. Masa relatywistyczna oddziałuje grawitacyjnie tak jak „zwykła” masa. Przykład 3. Znaleźć względną zmianę energii i częstotliwości fotonu wysłanego z Ziemi, który znalazł się na wysokości H =100 m nad Ziemią. Energia kwantu E = h (38), porównujemy ją z równoważną energią relatywistyczną. (39) (40)

Różnica potencjałów - Vg Różnica energii potencjalnej m Vg = mg. H = - częstotliwość kwantu na powierzchni Ziemi, ’ - częstotliwość na wysokości H Wyrażenie to dzielimy przez h Względna zmiana częstotliwości i energii kwantu

Dla różnicy odległości 100 m Jest to efekt mierzalny (Paund, Rebke 1960). Wykorzystano promieniowanie , emitowane przez Fe 57. Efekt ten, jak również ugięcie promienia świetlnego w pobliżu Słońca o 1. 75’’ potwierdzają ogólną teorię względności. stała Plancka h = 6. 626 • 10 -34 J • s

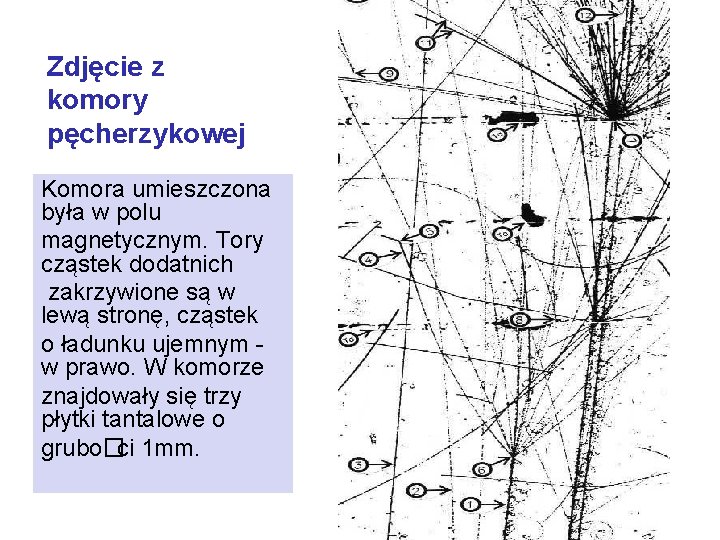
Komora pęcherzykowa Fotografia, stanowiąca tło pierwszej strony prof. Jana Pluty, przedstawia tory cząstek elementarnych i fragmentów jądrowych zarejestrowanych w komorze pęcherzykowej wypełnionej ciekłym propanem, C 3 H 8. Komora naświetlona była wiązką jąder węgla o pędzie 4. 2 Ge. V/c na nukleon. Zdjęcie pochodzi z Laboratorium Wysokich Energii Zjednoczonego Instytutu Badań Jądrowych w Dubnej koło Moskwy, gdzie przebywał prof. Jan Pluta, przez parę lat zajmując się także analizą podobnych temu zdjęć.

Zdjęcie z komory pęcherzykowej Komora umieszczona była w polu magnetycznym. Tory cząstek dodatnich zakrzywione są w lewą stronę, cząstek o ładunku ujemnym w prawo. W komorze znajdowały się trzy płytki tantalowe o grubo�ci 1 mm.

(12) - Punkt oddziaływania neutronu, tzw "gwiazda neutralna". (11) - Tory cząstek: szybkiej - prosty i jasny; powolnej - zakrzywiony i ciemny. (9) - Punkt konwersji fotonu na parę (elektron-pozyton). (Ta) - Płytka tantalowa (7) - Punkt oddziaływania jądra Węgla z jądrem Tantalu (C+Ta). W wyniku rozbicia ciężkiego jądra tantalu następuje emisja wielu cząstek i fragmentów jądrowych.

(8) - Piękny przykład konwersji fotonu w płytce tantalowej. Tor zakrzywiony w lewą stronę należy do pozytonu - cząstki antymaterii (4), (5) - Tor mezonu π (pi) o ładunku ujemnym. Gęstość jonizacji zwiększa się przy końcu toru, potem następuje wychwyt mezonu i jego pochłonięcie połączone z emisją protonu.

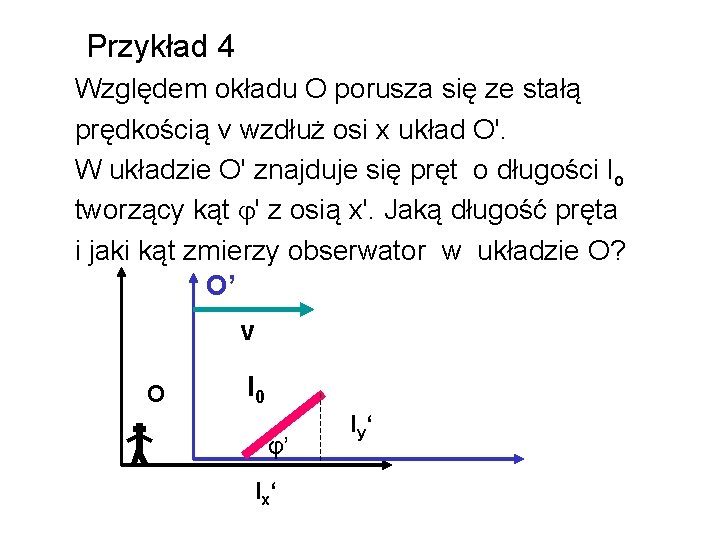
Przykład 4 Względem okładu O porusza się ze stałą prędkością v wzdłuż osi x układ O'. W układzie O' znajduje się pręt o długości lo tworzący kąt ' z osią x'. Jaką długość pręta i jaki kąt zmierzy obserwator w układzie O? O’ v O l 0 φ’ l x‘ l y‘

W układzie O’ rzuty długości na osie wynoszą: W układzie O:

Kąt nachylenia pręta zmierzony w układzie O:

Przykład 5 Czas życia mezonu + mierzony w układzie, w którym on spoczywa, wynosi 2, 5 10 -8 s. Jak wyjaśnić, że w odległości 100 m od miejsca ich powstania detektor wskazywał ich obecność? �� = 2, 5 10 -8 s czas w układzie własnym L = 100 m c = 3 · 108 m/s t – czas w układzie obserwatora zewnętrznego t = L/c = 100 m/ 3 · 108 m/s =0. 33 · 10 -6 m/s t > ��

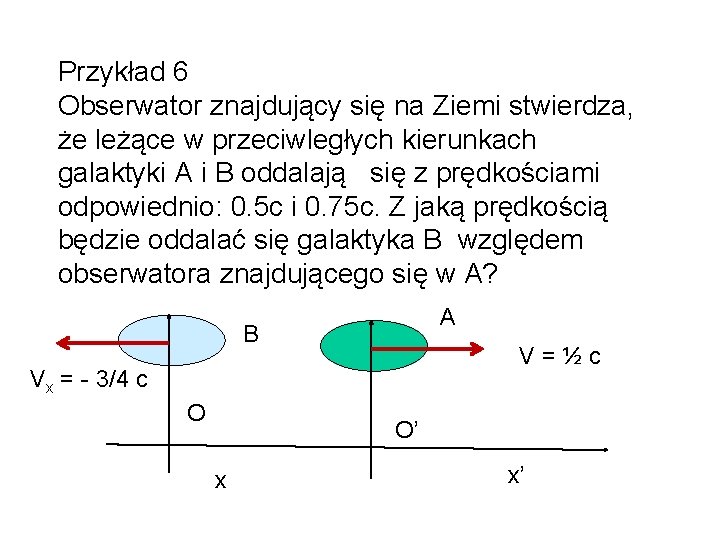
Przykład 6 Obserwator znajdujący się na Ziemi stwierdza, że leżące w przeciwległych kierunkach galaktyki A i B oddalają się z prędkościami odpowiednio: 0. 5 c i 0. 75 c. Z jaką prędkością będzie oddalać się galaktyka B względem obserwatora znajdującego się w A? A B V=½c Vx = - 3/4 c O O’ x x’

Galaktyka A związana z układem O’, B z - układem O Prędkość względna oddalania się Galaktyk:

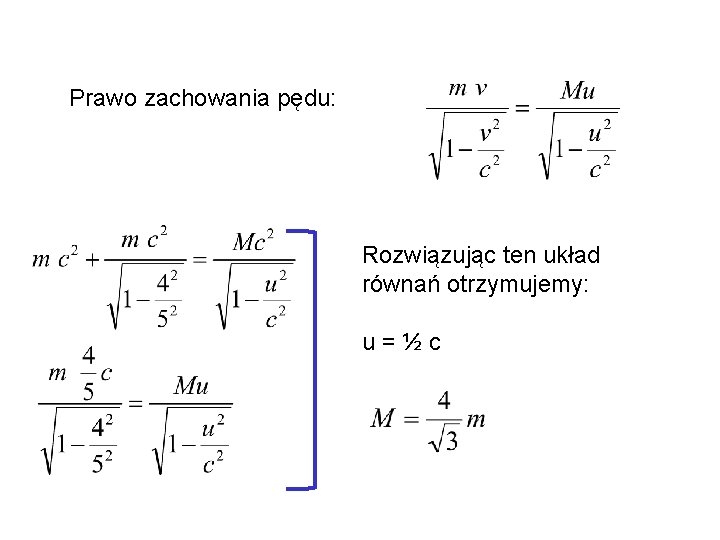
Przykład 7 Cząstka o masie spoczynkowej m, poruszająca się z prędkością 4/5 c, zderza się niesprężyście z inną, taką samą, będącą w spoczynku. W wyniku zderzenia powstaje jedna cząstka. Obliczyć jej masę spoczynkową i prędkość. v = 4/5 c M – masa powstałej w wyniku zderzenia cząstki u – prędkość powstałej w wyniku zderzenia cząstki Prawo zachowania energii:

Prawo zachowania pędu: Rozwiązując ten układ równań otrzymujemy: u=½c

Przykład 4 Czy Chrzest Polski i Bitwa pod Grunwaldem mogą w innym układzie odniesienia zaistnieć a) w tym samym miejscu, b) w tym samym czasie? Interwał czasoprzestrzenny: ( s)2 = (c t)2 - ( x)2 = (c t’)2 - ( x’)2 W naszym układzie odniesienia odległość miejsc chrztu i Bitwy x 500 km róznica w czasie t = 444 lata

W innym układzie odniesienia ( s’)2 = (c t’)2 - ( x’)2 a) x’ = 0 ( s’)2 = (c t’)2 - ( x’)2 ( s’)2 > 0 możliwe

b) t’ = 0 ( s’)2 = (c t’)2 - ( x’)2 ( s’)2 < 0 sprzeczność bo ( s)2 > 0 W innym układzie odniesienia nie może zajść w tym samym czasie Chrzest Polski i Bitwa pod Grunwaldem.
 Transformacje galileusza
Transformacje galileusza Odkrycia galileusza
Odkrycia galileusza Zasada względności galileusza
Zasada względności galileusza Przyspieszenie
Przyspieszenie Jak obliczyć przyspieszenie ziemskie za pomocą wahadła
Jak obliczyć przyspieszenie ziemskie za pomocą wahadła Przyspieszenie styczne i normalne
Przyspieszenie styczne i normalne Prędkość kątowa
Prędkość kątowa Prawo powszechnej grawitacji
Prawo powszechnej grawitacji Wzór na przyspieszenie
Wzór na przyspieszenie Legea atractiei universale a lui newton
Legea atractiei universale a lui newton Teoria endosymbiozy zakłada że mitochondria i plastydy
Teoria endosymbiozy zakłada że mitochondria i plastydy Taylor gilbreth
Taylor gilbreth Chester barnard teoria
Chester barnard teoria Teoria del ciclo vitale modigliani grafico
Teoria del ciclo vitale modigliani grafico Cs2no
Cs2no Desarrollo cognoscitivo en la adultez temprana
Desarrollo cognoscitivo en la adultez temprana Teoria topografica freud
Teoria topografica freud Big chill teoria
Big chill teoria Teoria de coesão e tensão
Teoria de coesão e tensão Compresion imagenes
Compresion imagenes Gra zeus
Gra zeus Frases de vigotsky sobre el aprendizaje
Frases de vigotsky sobre el aprendizaje Enfoque clasico expansionismo
Enfoque clasico expansionismo Photo
Photo Teoria de vigotsky
Teoria de vigotsky Teoria biogenetica
Teoria biogenetica La teoria celular
La teoria celular Devicia
Devicia Teoria del precedente
Teoria del precedente Gordon allport biography
Gordon allport biography Finanzas de corto plazo
Finanzas de corto plazo Teoria z
Teoria z Conclusión de la teoría del desarrollo moral de kohlberg
Conclusión de la teoría del desarrollo moral de kohlberg 14 bisogni henderson
14 bisogni henderson Descontinuidade de mohorovicic
Descontinuidade de mohorovicic Mecanismo de la evolución
Mecanismo de la evolución Materia
Materia Generacion espontanea
Generacion espontanea Teoria del condicionamiento sin reforzamiento
Teoria del condicionamiento sin reforzamiento Teoria de aristóteles
Teoria de aristóteles Teoria de juegos estrategias mixtas
Teoria de juegos estrategias mixtas Teoria etologica
Teoria etologica Linea de tiempo de la batalla de carabobo
Linea de tiempo de la batalla de carabobo Portata e sensibilità del termometro clinico
Portata e sensibilità del termometro clinico Zrazkova teoria
Zrazkova teoria Mario enrique guzman vega
Mario enrique guzman vega Teoria de charles dow
Teoria de charles dow Bandura teoria
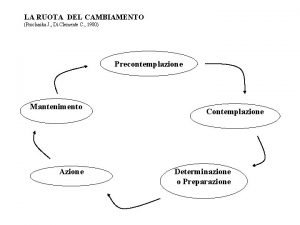
Bandura teoria Teoria della ruota del cambiamento
Teoria della ruota del cambiamento Teoria del rimbalzo elastico
Teoria del rimbalzo elastico Multietiologinen teoria
Multietiologinen teoria Teoria del jukebox emotivo
Teoria del jukebox emotivo Precursor del cognitivismo
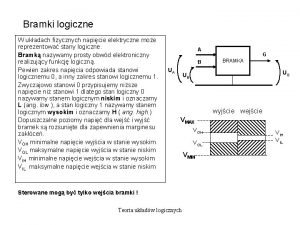
Precursor del cognitivismo Stany logiczne
Stany logiczne John stuart mill teoría
John stuart mill teoría Teoria cognitivista de piaget
Teoria cognitivista de piaget Teoria dowa
Teoria dowa Teoria coheso tenso transpiratoria
Teoria coheso tenso transpiratoria Teoria cuantitativa del dinero
Teoria cuantitativa del dinero Motivacin
Motivacin Bom senso
Bom senso Chester barnard teoria
Chester barnard teoria Kineticka teoria latok
Kineticka teoria latok