Estrategias Mixtas En teora de juegos una estrategia


























- Slides: 33

Estrategias Mixtas En teoría de juegos una estrategia mixta, a veces también llamada estrategia mezclada (del nombre en inglés mixed strategy), es una generalización de las estrategias puras, usada para describir la selección aleatoria de entre varias posibles estrategias puras, lo que determina siempre una distribución de probabilidad sobre el vector de estrategias de cada jugador. Una estrategia totalmente mixta es aquella en la que el jugador asigna una probabilidad estrictamente positiva a cada estrategia pura. Las estrategias totalmente mixtas son importantes para el refinamiento del equilibrio.

Ejemplo 1 – Estrategias Mixtas

Solución Ej. 1 (q) (1 -q) (p) (1 -p) En estrategias mixtas hay que hallar la función de pagos de cada jugador: Sacando factor común con la variable de decisión del jugador no. 1, tenemos:

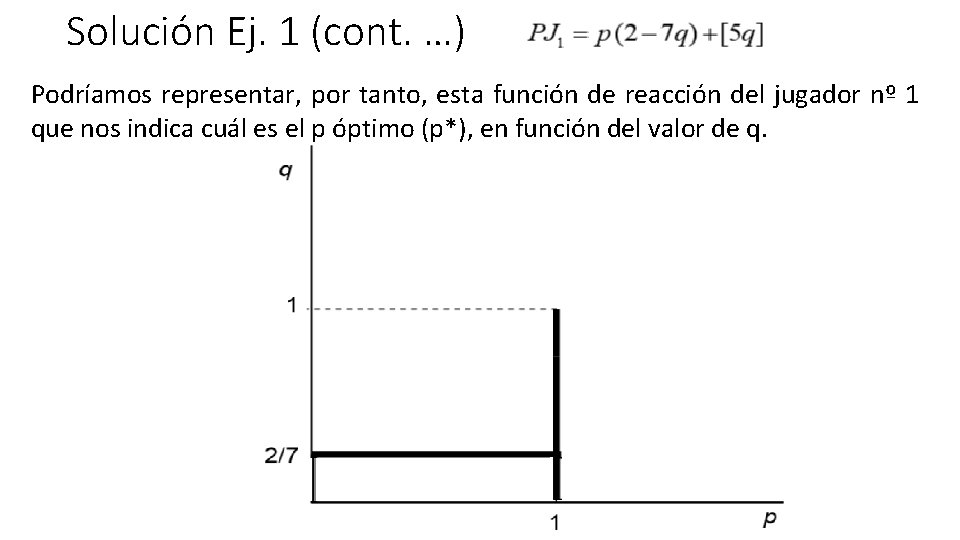
Solución Ej. 1 (cont. …) Lo representado entre corchetes va a obtenerlo el jugador nº 1 independientemente de cuál sea su elección – pues no depende de p –. El otro sumando es el que nos va a interesar para conocer cuál será su decisión óptima en función de lo que haga el otro. Fácilmente se puede apreciar que si q=2/7, el valor del paréntesis es cero, por lo que el jugador nº 1 será indiferente ante cualquier valor de p, pues eso no influirá en el pago que va a recibir. En otras palabras, si el jugador nº 2 opta por la estrategia X con probabilidad 2/7 y por la estrategia Y con probabilidad 5/7, el jugador nº 1 obtendrá el mismo pago utilizando la estrategia A o la estrategia B, o cualquier combinación lineal de ambas.

Solución Ej. 1 (cont. …) Por otro lado, si q tiene un valor inferior a 2/7, el valor del paréntesis será positivo, por lo que si el jugador nº 1 pretende maximizar su pago habrá de dar a p el valor más alto posible, es decir, tratándose como ocurre en este caso de una probabilidad, p debe valer 1. Finalmente, si q tiene un valor superior a 2/7, el valor del paréntesis será negativo, por lo que si el jugador nº 1 pretende maximizar su pago habrá de dar a p el valor más bajo posible, es decir, tratándose como ocurre en este caso de una probabilidad, p debe valer 0.

Solución Ej. 1 (cont. …) Podríamos representar, por tanto, esta función de reacción del jugador nº 1 que nos indica cuál es el p óptimo (p*), en función del valor de q.

Solución Ej. 1 (q) (1 -q) (p) (1 -p) Análogamente, la función de pagos del jugador nº 2 será: Sacando factor común la variable de decisión del jugador nº 2, tenemos:

Solución Ej. 1 Del mismo modo que ocurría con el jugador nº 1, lo representado entre corchetes va a obtenerlo el jugador nº 2 independientemente de cuál sea su elección – pues no depende de q –. El otro sumando es el que nos va a interesar para conocer cuál será su decisión óptima en función de lo que haga el otro jugador. Fácilmente se puede apreciar que, sea cual sea el valor de p, el valor del paréntesis es positivo – dado que p es una probabilidad y por tanto su valor está comprendido entre cero y uno –, por lo que el jugador nº 2, si pretende maximizar su pago, habrá de dar a q el valor más alto posible, es decir, tratándose como en este caso de una probabilidad, q debe valer 1.

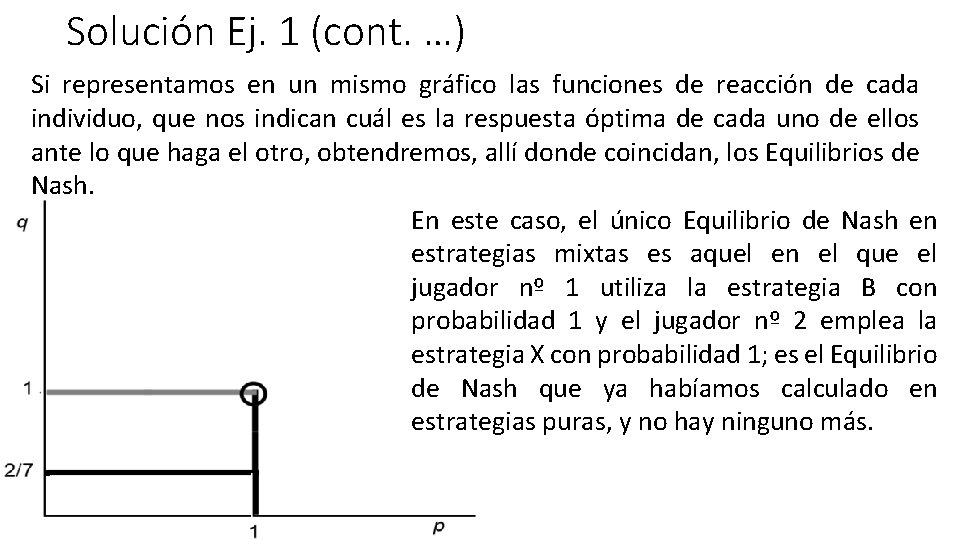
Solución Ej. 1 (cont. …) Podríamos representar, por tanto, esta función de reacción del jugador nº 2 que nos indica cuál es el q óptimo (q*), en función del valor de p.

Solución Ej. 1 (cont. …) Si representamos en un mismo gráfico las funciones de reacción de cada individuo, que nos indican cuál es la respuesta óptima de cada uno de ellos ante lo que haga el otro, obtendremos, allí donde coincidan, los Equilibrios de Nash. En este caso, el único Equilibrio de Nash en estrategias mixtas es aquel en el que el jugador nº 1 utiliza la estrategia B con probabilidad 1 y el jugador nº 2 emplea la estrategia X con probabilidad 1; es el Equilibrio de Nash que ya habíamos calculado en estrategias puras, y no hay ninguno más.

Ejemplo 2 – Estrategias Mixtas

Solución Ej. 2 (q) (1 -q) (p) (1 -p) Puede ocurrir, no obstante, que exista algún otro Equilibrio de Nash en estrategias mixtas. Sacando factor común la variable de decisión del jugador nº 1, tenemos:

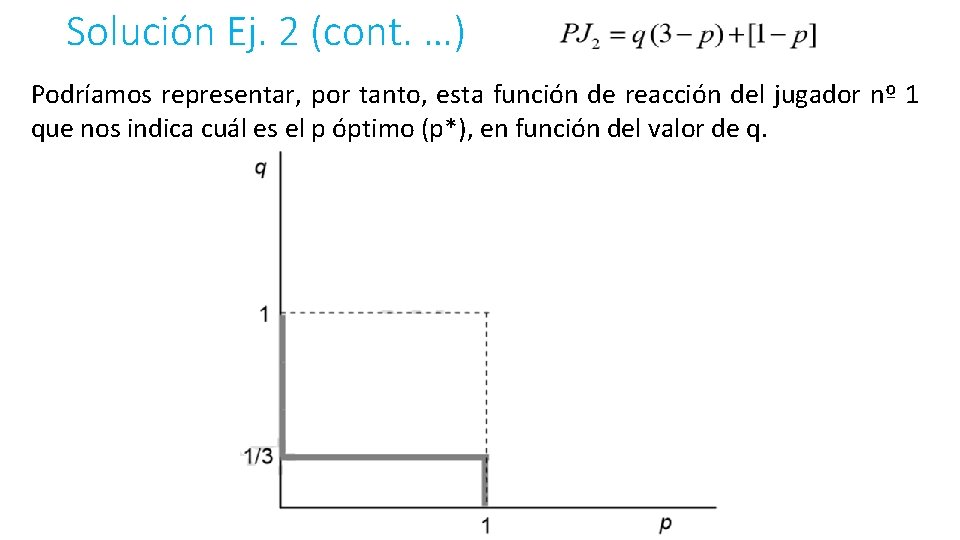
Solución Ej. 2 (cont. …) Como se puede apreciar, si q = 1/3, el valor del paréntesis es cero, por lo que el jugador nº 1 será indiferente ante cualquier valor de p, pues eso no influirá en el pago que va a recibir. Dicho de otro modo, si el jugador nº 2 opta por la estrategia X con probabilidad 1/3 y por la estrategia Y con probabilidad 2/3, el jugador nº 1 obtendrá el mismo pago utilizando la estrategia A o la estrategia B, o cualquier combinación lineal de ambas. Por otro lado, si q tiene un valor inferior a 1/3, el valor del paréntesis será positivo, por lo que si el jugador nº 1 pretende maximizar su pago habrá de dar a p el valor más alto posible, es decir, tratándose de una probabilidad, p debe valer 1. Finalmente, si q tiene un valor superior a 1/3, el valor del paréntesis será negativo, por lo que si el jugador nº 1 pretende maximizar su pago habrá de dar a p el valor más bajo posible, es decir, tratándose de una probabilidad, p deberá valer 0.

Solución Ej. 2 (cont. …) Podríamos representar, por tanto, esta función de reacción del jugador nº 1 que nos indica cuál es el p óptimo (p*), en función del valor de q.

Solución Ej. 2 (q) (1 -q) (p) (1 -p) Análogamente, la función de pagos del jugador nº 2 será: Sacando factor común la variable de decisión del jugador nº 2, tenemos:

Solución Ej. 2 Del mismo modo que ocurría con el jugador nº 1, lo representado entre corchetes va a obtenerlo el jugador nº 2 independientemente de cuál sea su elección – pues no depende de q –. El otro sumando es el que, por tanto, nos va a interesar para conocer cuál será su decisión óptima en función de lo que haga el otro jugador. Fácilmente se puede apreciar que si p es 2/3, el valor del paréntesis será cero, por lo que el jugador nº 2 estará indiferente por el valor de q, dado que siempre obtendrá el mismo pago sea cual sea éste. Si p es menor de 2/3 el valor del paréntesis será positivo, por lo que lo óptimo para el jugador nº 2 será otorgar a q el valor 1 (es decir, utilizar la estrategia X), mientras que si p es mayor de 2/3, dado que el valor del paréntesis será negativo, debería utilizar la estrategia Y (o lo que es lo mismo, dar a q el valor cero).

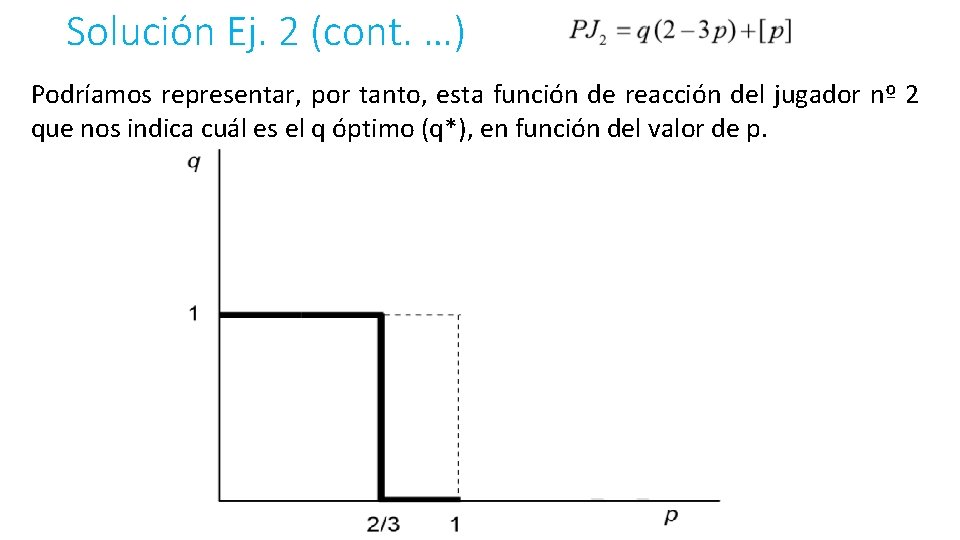
Solución Ej. 2 (cont. …) Podríamos representar, por tanto, esta función de reacción del jugador nº 2 que nos indica cuál es el q óptimo (q*), en función del valor de p.

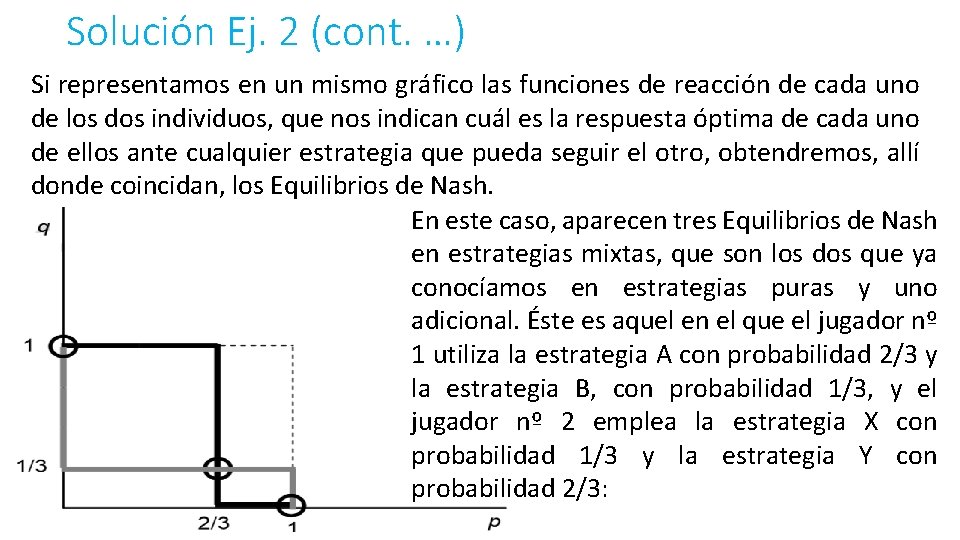
Solución Ej. 2 (cont. …) Si representamos en un mismo gráfico las funciones de reacción de cada uno de los dos individuos, que nos indican cuál es la respuesta óptima de cada uno de ellos ante cualquier estrategia que pueda seguir el otro, obtendremos, allí donde coincidan, los Equilibrios de Nash. En este caso, aparecen tres Equilibrios de Nash en estrategias mixtas, que son los dos que ya conocíamos en estrategias puras y uno adicional. Éste es aquel en el que el jugador nº 1 utiliza la estrategia A con probabilidad 2/3 y la estrategia B, con probabilidad 1/3, y el jugador nº 2 emplea la estrategia X con probabilidad 1/3 y la estrategia Y con probabilidad 2/3:

Solución Ej. 2 (cont. …) El E. N. que figura en la parte superior izquierda del gráfico es en el que p vale cero y el valor de q es 1; es decir, (B, X). El de la parte inferior derecha se produce para los valores de uno y cero p y de q, respectivamente, por lo que se trata del E. N. ( A, Y).

Jugador No. 1 Jugador No. 2 L R T 2, 1 0, 2 B 1, 2 3, 0

Estrategias Mixtas u(T/q) = 2 q + 0(1 -q) = 2 q u(B/q) = 1 q + 3(1 -q) = q+3 -3 q = -2 q+3 2 q >-2 q+3, 4 q>3, q>3/4 Si la probabilidad de que J 2 elija L es >3/4 entonces, el J 1 eligirá T Si la probabilidad de que J 2 elija L es <3/4 entonces, el J 1 eligirá B u(L/p) = 1 p + 2(1 -p) = p+2 – 2 p = -p + 2 u(R/p) = 2 p + 0(1 -p) = 2 p P+2>2 p, 2>3 p, 3 p<2, p<2/3 Si la probabilidad de que J 1 elija T es <2/3 entonces, el J 2 eligirá L Si la probabilidad de que J 1 elija B es >2/3 entonces, el J 2 eligirá R ENEM = 2/3 T+1/3 B, 3/4 L+1/4 R


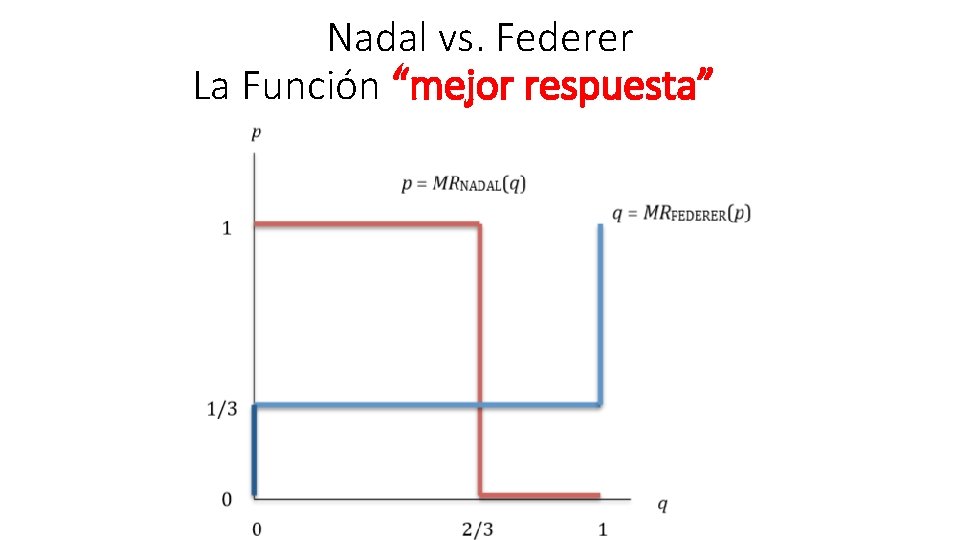
Nadal vs. Federer Cálculo del EN 1. - Sea q la probabilidad con la que Federer juega I (izquierda), veamos qué prefiere Nadal: u. NADAL(I/q) = 0. 5 q + 0. 9(1−q) = 0. 9 − 0. 4 q u. NADAL(D/q) = 0. 7 q + 0. 5(1−q) = 0. 5 + 0. 2 q Para que Nadal esté indeciso, debemos tener: 0. 9 − 0. 4 q > 0. 5 + 0. 2 q q = 2/3

Nadal vs. Federer Cálculo del EN Sea p la probabilidad con la que Nadal juega I, veamos qué prefiere Federer: u. FEDERER(I/p) = 0. 5 p + 0. 3(1−p) = 0. 3 + 0. 2 q u. FEDERER(D/p) = 0. 1 p + 0. 5(1−p) = 0. 5 − 0. 4 p Para que Federer esté indeciso, debemos tener: 0. 3 + 0. 2 p > 0. 5 − 0. 4 p p = 1/3 Escribiremos así el equilibrio: E. N. E. M:

Nadal vs. Federer La Función “mejor respuesta” La función mejor respuesta de Nadal nos debe decir cuál es su mejor estrategia para cada posible estrategia mixta de Federer: De igual manera calculamos la MR para Federer:

Nadal vs. Federer La Función “mejor respuesta”

Juego del Gallina En la película ‘Rebelde sin causa’, James Dean participa en el ‘juego del gallina’ con otro adolescente: Cada uno conduce a toda velocidad un coche hacia un acantilado; el primero que salta de su coche es un ‘gallina’. Suponga que los dos prefieren ser el último en saltar, pero también saltar primero a no saltar, para así evitar despeñarse. En tal caso, podemos representar el juego en forma estratégica como (nota: Que los dos salten ‘los últimos’ se interpreta como que ninguno salta; que los dos salten ‘los primeros’ significa que los dos saltan al mismo tiempo):

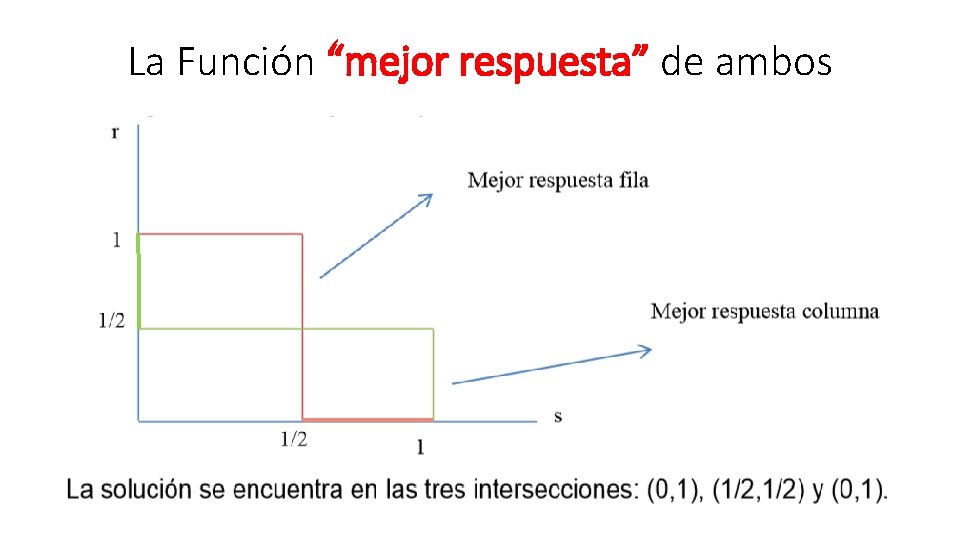
Halle los equilibrios de Nash en estrategias mixtas La utilidad esperada del jugador 1 (fila) es:

Halle los equilibrios de Nash en estrategias mixtas La utilidad esperada del jugador 2 (columna) es:

La Función “mejor respuesta” de ambos

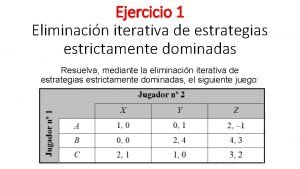
Ejercicios Estrategias Mixtas 1 Jugador No. 2

Ejercicios Estrategias Mixtas 2 Jugador No. 1 Jugador No. 2

Jugador No. 1 Solución Ej. 1 Jugador No. 2 En estrategias mixtas hay que hallar la función de pagos de cada jugador, y desarrollar el ejercicio de la manera siguiente:
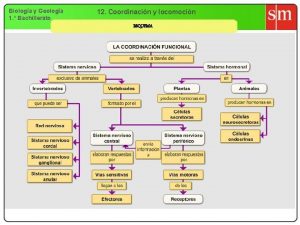
 Juegos con estrategias mixtas
Juegos con estrategias mixtas La teora
La teora Rayo es una palabra aguda grave o esdrujula
Rayo es una palabra aguda grave o esdrujula Actividad generadora de información previa
Actividad generadora de información previa Estrategias metacognitivas
Estrategias metacognitivas Ejercicio
Ejercicio Plan de marketing de chocolates
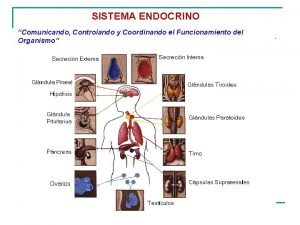
Plan de marketing de chocolates Mecanismo de accion de las hormonas
Mecanismo de accion de las hormonas Glandulas mixtas
Glandulas mixtas Fraciones mixtas
Fraciones mixtas Ejemplos de preguntas mixtas
Ejemplos de preguntas mixtas Losas mixtas
Losas mixtas Trampas mixtas o combinadas
Trampas mixtas o combinadas Defensas combinadas baloncesto
Defensas combinadas baloncesto Fracciones propias, impropias y mixtas
Fracciones propias, impropias y mixtas Placas continentales oceanicas y mixtas
Placas continentales oceanicas y mixtas Sistema solar
Sistema solar Periodicas puras y mixtas
Periodicas puras y mixtas Convertir número mixto a fracción impropia y viceversa
Convertir número mixto a fracción impropia y viceversa Preguntas mixtas
Preguntas mixtas Silabas mixtas
Silabas mixtas Benzomorfan
Benzomorfan Fracciones mixtas
Fracciones mixtas Integrales con limites infinitos
Integrales con limites infinitos Clasificación de las ondas
Clasificación de las ondas Estrategia de encogimiento
Estrategia de encogimiento Productos en etapa de introducción
Productos en etapa de introducción Pico ebm
Pico ebm Las 5 ps de la estrategia
Las 5 ps de la estrategia Estratégia dominante teoria dos jogos
Estratégia dominante teoria dos jogos Cobranza efectiva
Cobranza efectiva Estrategia flanqueo
Estrategia flanqueo Estrategia de enseñanza-aprendizaje
Estrategia de enseñanza-aprendizaje Componentes de la estrategia multimodal
Componentes de la estrategia multimodal