Szczeglny limak Paskala szczeglna epicykloida Kardioida w optyce

Szczególny ślimak Paskala, szczególna epicykloida Kardioida w optyce 1/9 Krzywe o równaniu {y–a·|x|2/3}2 = b–x 2 mają dla pewnych wartości parametrów a, b (np. dla a= ½, ¾ i 1, gdy b= ¾) kształt serca. Jednak to nie im przysługuje, wywiedziona z greckiego słowa kardi = serce, nazwa kardioida. Słowo kardioida po raz pierwszy użył, w r. 1741, Johann Castillon w odniesieniu do krzywej, która jest zarówno pewną konchoidą okręgu jak i pewną epicykloidą (mianowicie zakreślaną przez punkt okręgu toczącego się po zewnętrznej stronie okręgu mającego taki sam promień). Konchoidy okręgu to krzywe, które badał Étienne Pascal (1588 -1651), ojciec Błażeja. Gilles Roberval nazwał je ślimakami Paskala. Cykloidy - krzywe powstające w wyniku toczenia okręgu po prostej - budziły zainteresowanie już Arystotelesa (384 -322 p. n. e. ). Cykloidami i ich uogólnieniami zajmowali się potem m. in. . Johann Kepler (1571 -1630), Bonaventura Cavalieri (1598 -1647) i Christopher Wren, który - w r. 1658 - pierwszy wyliczył długość łuku cykloidy. W r. 1674 kardioidę badał – poszukując optymalnego profilu dla przekładni zębowych – duński astronom Ole Christensen Roemer, nota bene autor terminu epicykloida W r. 1708 jej długość wyliczył Phillippe de la Hire. My przyjrzymy się, jak kardioida pojawia się w pewnym zadaniu z optyki.

Kardioida sfotografowana w kubku z kawą z mlekiem Kardioida w optyce 2/9 fot. Piotr Kuświk Tak jak to widać na fotografii obok, odpowiednie oświetlnie zarysowało na powierzchni płynu nietuzinkowy kształt. Pokażemy, że (pomijając tu dość już słabe efekty wyższego stopnia, tj. odbicia rzędu 2 i wyższe, oraz przymykając oko na silną ingerencję lampy błyskowej i dalekie od idealnego umieszczenie źródła odbijanych promienie) ów kształt to kardioida. p 1. Z początku układu współrzędnych zatoczmy okrąg o dowolnym promieniu a. Ma on równanie x 2 + y 2 = a 2. p 2. Z punktu A = (– a, 0) wysyłamy promień nachylony do osi Ox pod kątem α. p 3. Promień dociera do okręgu w punkcie, który oznaczamy przez B. Tu się odbija i podąża w kierunku punktu C. Napiszemy równania promieni padającego i odbitego oraz wykażemy, że obwiednią rodziny promieni odbitych jest właśnie kardioida.

Równanie promieni padającego Kardioida w optyce 3/9 p 4. Promień padający ma równanie y = tg(α)·(x+a). p 5. Zatem współrzędne punktu B wyznaczymy z układu równań y = tg(α)·(x+a), x 2 + y 2 = a 2. Otrzymujemy x 2 +{tgα·(x+a)}2 = r 2 , tj. {1+tg 2α}·x 2 + 2 a·tg 2α·x + {1–tg 2α}·a 2 = 0. p 6. Równanie to ma dwa zera: x = –a oraz x = a·{tg 2α– 1}/{tg 2α+1} = a·cos(2α). Pierwsze (tzn. x = – a) wyznacza punkt A, drugie jest odciętą punktu B. p 7. Wstawiając tę odciętą do równania okręgu natychmiast otrzymujemy rzędną punktu B. I w ten sposób wiemy już, że B = (a·cos(2α), a·sin(2α)). Znamy już równanie promienia wysyłanego z punkty A i współrzędne punktu B, w którym dobiega on do półokręgu. Teraz czas na równanie promienia odbitego.

Równanie promieni odbitego Kardioida w optyce 4/9 p 8. Połączmy punkt B ze środkiem O okręgu. Ponieważ |AO| = |OB. |, więc otrzymany trójkąt AOB jest równoramienny i dlatego kąt przy wierzchołku B jest równy α. p 9. Trzeci kąt w AOB jest równy 180°– , w konsekwencji czego odcinek OB jest nachylony do osi Ox pod kątem 2. p 10. CBO = OBA = (wszak kąt odbicia jest równy kątowi padania), więc odcinek BC jest nachylony do osi Ox pod kątem 180°–{180°–(2 + )} = 3. p 11. Leży zatem odcinek BC na prostej o równaniu y = a·sin(2α)+tg(3 )·(x–a·cos(2α)}. p 12. Powyższe równanie obejmuje jednego przypadku – gdy α = 60º (wtedy promień BC biegnie równolegle do osi Ox). Nie jest on wykluczony przedstawieniu wektorowym prostej BC: x(t) = a·cos(2α) + cos(3α)·t, y(t) = a ·sin(2α) + sin(3α)·t. Powyższe równanie opisuje rodzinę promieni odbitych. Aby przejrzyście wyrysować przedstawicieli tej rodziny (uzyskujemy ich dla konkretnych wartości kąta α (-90º, 90º)), należy wyznaczyć współrzędne punktów C (tutaj promień odbity dobiega do okręgu) i D (tutaj przecina oś poziomą Ox).

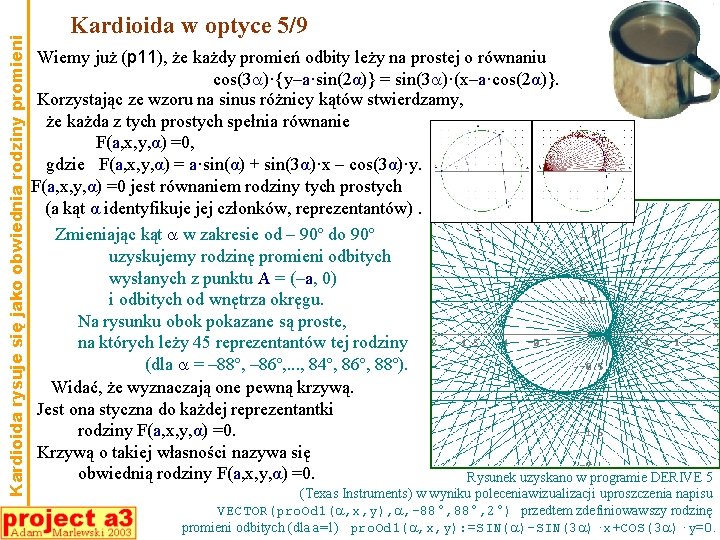
Kardioida rysuje się jako obwiednia rodziny promieni Kardioida w optyce 5/9 Wiemy już (p 11), że każdy promień odbity leży na prostej o równaniu cos(3 )·{y–a·sin(2α)} = sin(3 )·(x–a·cos(2α)}. Korzystając ze wzoru na sinus różnicy kątów stwierdzamy, że każda z tych prostych spełnia równanie F(a, x, y, α) =0, gdzie F(a, x, y, α) = a·sin(α) + sin(3α)·x – cos(3α)·y. F(a, x, y, α) =0 jest równaniem rodziny tych prostych (a kąt α identyfikuje jej członków, reprezentantów). Zmieniając kąt w zakresie od – 90º do 90º uzyskujemy rodzinę promieni odbitych wysłanych z punktu A = (–a, 0) i odbitych od wnętrza okręgu. Na rysunku obok pokazane są proste, na których leży 45 reprezentantów tej rodziny (dla = – 88º, – 86º, . . . , 84º, 86º, 88º). Widać, że wyznaczają one pewną krzywą. Jest ona styczna do każdej reprezentantki rodziny F(a, x, y, α) =0. Krzywą o takiej własności nazywa się obwiednią rodziny F(a, x, y, α) =0. Rysunek uzyskano w programie DERIVE 5 (Texas Instruments) w wyniku poleceniawizualizacji uproszczenia napisu VECTOR(pro. Od 1( , x, y), , -88°, 2°) przedtem zdefiniowawszy rodzinę promieni odbitych (dla a=1) pro. Od 1( , x, y): =SIN( )-SIN(3 )·x+COS(3 )·y=0.

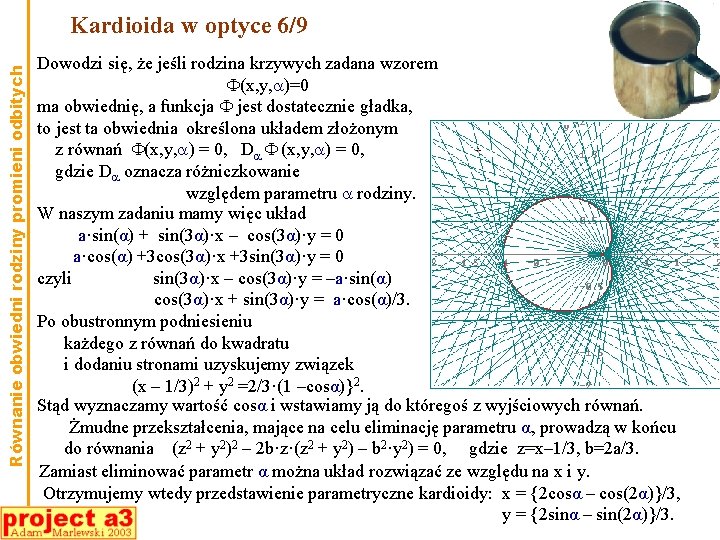
Równanie obwiedni rodziny promieni odbitych Kardioida w optyce 6/9 Dowodzi się, że jeśli rodzina krzywych zadana wzorem (x, y, )=0 ma obwiednię, a funkcja jest dostatecznie gładka, to jest ta obwiednia określona układem złożonym z równań (x, y, ) = 0, D (x, y, ) = 0, gdzie D oznacza różniczkowanie względem parametru rodziny. W naszym zadaniu mamy więc układ a·sin(α) + sin(3α)·x – cos(3α)·y = 0 a·cos(α) +3 cos(3α)·x +3 sin(3α)·y = 0 czyli sin(3α)·x – cos(3α)·y = –a·sin(α) cos(3α)·x + sin(3α)·y = a·cos(α)/3. Po obustronnym podniesieniu każdego z równań do kwadratu i dodaniu stronami uzyskujemy związek (x – 1/3)2 + y 2 =2/3·(1 –cosα)}2. Stąd wyznaczamy wartość cosα i wstawiamy ją do któregoś z wyjściowych równań. Żmudne przekształcenia, mające na celu eliminację parametru α, prowadzą w końcu do równania (z 2 + y 2)2 – 2 b·z·(z 2 + y 2) – b 2·y 2) = 0, gdzie z=x– 1/3, b=2 a/3. Zamiast eliminować parametr α można układ rozwiązać ze względu na x i y. Otrzymujemy wtedy przedstawienie parametryczne kardioidy: x = {2 cosα – cos(2α)}/3, y = {2 sinα – sin(2α)}/3.

Współrzędne punktów C i D Kardioida w optyce 7/9 p 13. Współrzędne punktu C uzyskujemy tworząc układ x 2 + y 2 = a 2 x = a·cos(2α) + cos(3α)·t, y = a·sin(2α) + sin(3α)·t złożony z równania okręgu i pary równań opisujących wektorowo prostą BC (przy tym kąta α = 60º nie rozpatrujemy, gdyż dlań BC jest równoległe do osi Ox). Pierwsze z trzech powyższych równań przyjmuje postać {r·cos(2α) + cos(3α)·t}2 +{r·sin(2α) + sin(3α)·t}2 = r 2. Jego rozwiązaniami są t = 0 i t = – 2 r·cos. Pierwsze z nich daje punkt B, drugie – poszukiwane współrzędne punktu C: x = r·cos(2α) + cos(3α)·{– 2 r·cos )} = –r·cos(4α), y = r·sin(2α) + sin(3α)·{– 2 r·cos )} = –r·sin(4α). p 14. Odciętą punkt D uzyskujemy wstawiając do równania prostej BC, tzn. do równania y = a·sin(2α)+tg(3 )·(x–a·cos(2α)}, wartość y = 0 (jako że D leży na osi Ox). Stąd, nadal przy założeniu, iż α 60 , otrzymujemy D = ( r·cos(2α)·{1–tg(2α)·tg(3α)}, 0).

Uzyskanie ilustracji w systemie DERIVE 5 (Texas Instrs) Kardioida w optyce 8/9 "_kardi. Op. MTH kardioida jako obwiednia promieni odbitych (A. Marlewski 14. 11. 2002)" [Case. Mode: =Sensitive, Input. Mode: =Word] promien. Padajacy(r, alpha, t): =[-r, 0]+[COS(alpha), SIN(alpha)]*t punkt. B(r, alpha): =r*[COS(2*alpha), SIN(2*alpha)] promien. Odbity(r, alpha, t): =punkt. B(r, alpha)+[COS(3*alpha), SIN(3*alpha)]*t punkt. D(r, alpha): =IF(alpha/=pi/3, promien. Odbity(r, alpha, r*SIN(2*alpha)/SIN(3*alpha)), r/2*[1, SQRT(3)]) punkt. C(r, alpha): =promien. Odbity(r, alpha, -2*r*COS(alpha)) punkt. D(r, alpha): =promien. Odbity(r, alpha, r*SIN(2*alpha)/SIN(3*alpha)) wez. Wedlug. Wiekszej. Rzednej(P, Q): =IF(P SUB 2>Q SUB 2, P, Q) punkt. E(r, alpha): =wez. Wedlug. Wiekszej. Rzednej (punkt. C(r, alpha), punkt. D(r, alpha)) "Definicja promienia padajacego i odbitego (konczacego sie na okregu lub osi Ox): " od. Ado. E(r, alpha): =[[-r, 0], punkt. B(r, alpha), punkt. E(r, alpha)] "Rownanie okregu o srodku w [0, 0] i promieniu 3, nastepnie Plot: " x^2+y^2=3^2 "Simplify Approximate, otrzymana macierz Plot: " VECTOR(od. Ado. E(3, alpha), alpha, 2*deg, 89*deg, 3*deg) "Definicja wektorowa kardioidy: " para_kardioida(C, a, t): =C+2*a*[COS(t), SIN(t)] -a*[COS(2*t), SIN(2*t)] "Simplify Basic, nastepnie Plot (od -Pi do Pi): " para_kardioida([0, 0], 1, t)

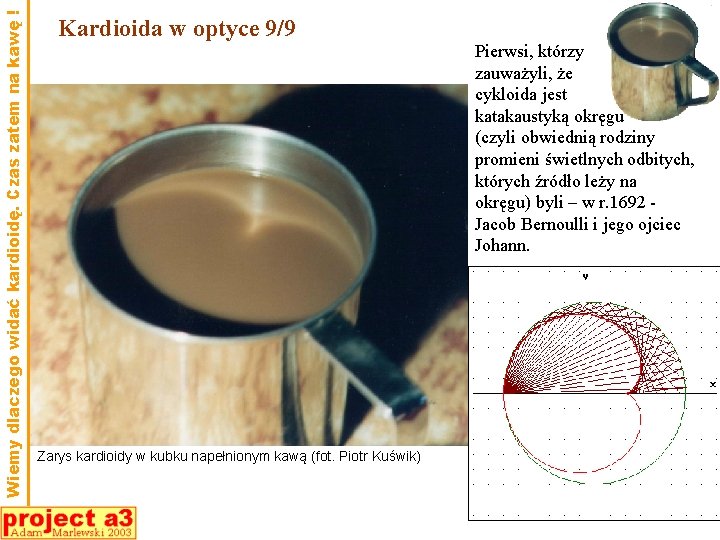
Wiemy dlaczego widać kardioidę. Czas zatem na kawę ! Kardioida w optyce 9/9 Zarys kardioidy w kubku napełnionym kawą (fot. Piotr Kuświk) Pierwsi, którzy zauważyli, że cykloida jest katakaustyką okręgu (czyli obwiednią rodziny promieni świetlnych odbitych, których źródło leży na okręgu) byli – w r. 1692 Jacob Bernoulli i jego ojciec Johann.