Kompilatory optymalizujce Wykad 7 2 godz Podstawowe transformacje




![Lokalność kodu Przechowywanie tablicy A kolumnami: A[1, 1] A[2, 1] … A[1, 2] A[2, Lokalność kodu Przechowywanie tablicy A kolumnami: A[1, 1] A[2, 1] … A[1, 2] A[2,](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-5.jpg)
![Wymiana pętli Przechowywanie tablicy A kolumnami: A[1, 1] A[2, 1] … A[1, 2] A[2, Wymiana pętli Przechowywanie tablicy A kolumnami: A[1, 1] A[2, 1] … A[1, 2] A[2,](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-6.jpg)



![Połączenie pętli(fusion) for i = 1, 1000 A[i] = B[i] + 3 end_for j Połączenie pętli(fusion) for i = 1, 1000 A[i] = B[i] + 3 end_for j](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-10.jpg)
![Podział pętli(fission) for i = 1, 1000 A[i] = A[i-1] + 3 C[i] = Podział pętli(fission) for i = 1, 1000 A[i] = A[i-1] + 3 C[i] =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-11.jpg)


![Zastosowanie zmiennej skalarnej do i = 2, N+1 B[i] = A[i-1]+1 enddo do i=2, Zastosowanie zmiennej skalarnej do i = 2, N+1 B[i] = A[i-1]+1 enddo do i=2,](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-14.jpg)





![Rozwijanie pętli(loop un-roll) for i = 1, 10 a[i] = b[i]; *p =. . Rozwijanie pętli(loop un-roll) for i = 1, 10 a[i] = b[i]; *p =. .](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-20.jpg)





![Partycjonowanie przestrzeni Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] = Partycjonowanie przestrzeni Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-26.jpg)
![Partycjonowanie czasu Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] = Partycjonowanie czasu Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-27.jpg)
![Transformacja przestrzeni Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] = Transformacja przestrzeni Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-28.jpg)
![Wymiana pętli for i = 1, 100 for j = 1, 200 A[i, j] Wymiana pętli for i = 1, 100 for j = 1, 200 A[i, j]](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-31.jpg)











![Scalenie Pętli Przykład: for (i=0; B[i] = for (j=0; C[j] = i<N; i++) f(A[i]); Scalenie Pętli Przykład: for (i=0; B[i] = for (j=0; C[j] = i<N; i++) f(A[i]);](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-46.jpg)






![Odwrócenie iteracji pętli (Loop Reversal) Ø p=N-i for (i=0; i<N; i++){ a[i]=b[i]+1; c[i]=a[i]/2; } Odwrócenie iteracji pętli (Loop Reversal) Ø p=N-i for (i=0; i<N; i++){ a[i]=b[i]+1; c[i]=a[i]/2; }](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-54.jpg)
![Odwrócenie iteracji pętli może zwiększyć lokalność for (i=0; i<=N; i++) for. B[i] I = Odwrócenie iteracji pętli może zwiększyć lokalność for (i=0; i<=N; i++) for. B[i] I =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-55.jpg)

![for (i=0; i<N; i++) for (j=0; j<M; j++) A[i+1][j] = f(A[i][j+1]); i Prz eko for (i=0; i<N; i++) for (j=0; j<M; j++) A[i+1][j] = f(A[i][j+1]); i Prz eko](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-58.jpg)
![Blokowanie(1 -D ) i Blokowanie 1 -D j i for(i=0; i<9; i++) A[i] =. Blokowanie(1 -D ) i Blokowanie 1 -D j i for(i=0; i<9; i++) A[i] =.](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-59.jpg)

![Blokowanie 2 -D for(i=0; i<N; i++) for(j=0; j<N; j++) A[i][j] = B[j][i]; for(TI=0; TI<N; Blokowanie 2 -D for(i=0; i<N; i++) for(j=0; j<N; j++) A[i][j] = B[j][i]; for(TI=0; TI<N;](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-61.jpg)


- Slides: 65

Kompilatory optymalizujące Wykład 7, 2 godz. Podstawowe transformacje pętli © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 1

Plan 1. 2. 3. 4. 5. 6. Hierarchia pamięci Przechowywanie tablicy (kolumnami lub wierszami) a lokalność kodu Funkcja afiniczna indeksów tablicy, postać matematyczna Partycjonowania afiniczne : odwzorowanie iteracji na procesor/wątek, czas logiczny wykonywania iteracji, iteracje w innej przestrzeni Rola eliminacji Fouriera-Motzkina w transformacjach afinicznych Stare i nowe wektory dystansu, obliczenie nowego wektora dystansu, jego zastosowanie celem sprawdzenia legalności transformacji © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 2

Plan, cd 7. Najważniejsze transformacje oraz ich przydatność w kompilatorach optymalizujących Podział Pętli Scalenie Pętli Wymiana Pętli Odwrócenie iteracji Przekoszenie iteracji pętli Blokowanie Rozszerzenie skalara © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 3

Hierarchia pamięci CPU Cache L 1 Cache L 2 Cache L 3 Memory 4
![Lokalność kodu Przechowywanie tablicy A kolumnami A1 1 A2 1 A1 2 A2 Lokalność kodu Przechowywanie tablicy A kolumnami: A[1, 1] A[2, 1] … A[1, 2] A[2,](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-5.jpg)
Lokalność kodu Przechowywanie tablicy A kolumnami: A[1, 1] A[2, 1] … A[1, 2] A[2, 2] … A[1, 3] … for i = 1, 100 for j = 1, 200 A[i, j] = A[i, j] + 3 end_for Pętla ma niską lokalność przestrzenną ponieważ każda nowa iteracja odwołuje sie do innej linijki cache. 5
![Wymiana pętli Przechowywanie tablicy A kolumnami A1 1 A2 1 A1 2 A2 Wymiana pętli Przechowywanie tablicy A kolumnami: A[1, 1] A[2, 1] … A[1, 2] A[2,](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-6.jpg)
Wymiana pętli Przechowywanie tablicy A kolumnami: A[1, 1] A[2, 1] … A[1, 2] A[2, 2] … for i = 1, 100 for j = 1, 200 A[i, j] = A[i, j] + 3 end_for A[1, 3] … for j = 1, 200 for i = 1, 100 A[i, j] = A[i, j] + 3 end_for Druga pętla ma lepszą lokalność przestrzenną ponieważ kolejne odwołania mamy do tej samej linijki cache. 6

Kiedy można wymieniać pętle? for i = 2, 100 for j = 1, 200 A[i, j] = A[i-1, j+1]+3 end_for j i Istnieje zależność (3, 3) -> (4, 2) 7

Kiedy można wymieniać pętle? Wymieniać pętle można wtedy i tylko wtedy, gdy wszystkie elementy wektora dystansu są nieujemne j i Istnieje zależność (3, 3) -> (4, 2) 8

Wymiana pętli Wektor dystansu: (1, -1) = (4, 2)-(3, 3) n Wymiana pętli nie jest możliwa n j i 9
![Połączenie pętlifusion for i 1 1000 Ai Bi 3 endfor j Połączenie pętli(fusion) for i = 1, 1000 A[i] = B[i] + 3 end_for j](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-10.jpg)
Połączenie pętli(fusion) for i = 1, 1000 A[i] = B[i] + 3 end_for j = 1, 1000 C[j] = A[j] + 5 end_for i = 1, 1000 A[i] = B[i] + 3 C[i] = A[i] + 5 end_for Lepsza lokalność czasowa względem tablicy A[i]: produkowana wartość natychmiast jest konsumowana. 10
![Podział pętlifission for i 1 1000 Ai Ai1 3 Ci Podział pętli(fission) for i = 1, 1000 A[i] = A[i-1] + 3 C[i] =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-11.jpg)
Podział pętli(fission) for i = 1, 1000 A[i] = A[i-1] + 3 C[i] = B[i] + 5 end_for i = 1, 1000 A[i] = A[i-1] + 3 end_for i = 1, 1000 C[i] = B[i] + 5 end_for Drugą pętlę można zrównoleglić 11

Blokowanie rejestru(register blocking) for j = 1, 2*m for i = 1, 2*n A[i, j] = A[i-1, j] + A[i-1, j-1] end_for for j = 1, 2*m, 2 for i = 1, 2*n, 2 A[i, j] = A[i-1, j] + A[i-1, j-1] A[i, j+1] = A[i-1, j+1] + A[i-1, j] A[i+1, j] = A[i, j] + A[i, j-1] A[i+1, j+1] = A[i, j+1] + A[i, j] end_for Ciało drugiej pętli składa się z czterech iteracji: dwóch pierwszej pętli i dwóch drugiej pętli 12 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT

Blokowanie rejestru(register blocking) for j = 1, 2*m for i = 1, 2*n A[i, j] = A[i-1, j] + A[i-1, j-1] end_for 13 for j = 1, 2*m, 2 for i = 1, 2*n, 2 A[i, j] = A[i-1, j] + A[i-1, j-1] A[i, j+1] = A[i-1, j+1] + A[i-1, j] A[i+1, j] = A[i, j] + A[i, j-1] A[i+1, j+1] = A[i, j+1] + A[i, j] end_for Zwiększa lokalność tablicy A: produkowane wartości mogą być przechowywane w rejestrach i natychmiast© Włodzimierz konsumowane Bielecki, Piotr Błaszyński WI ZUT
![Zastosowanie zmiennej skalarnej do i 2 N1 Bi Ai11 enddo do i2 Zastosowanie zmiennej skalarnej do i = 2, N+1 B[i] = A[i-1]+1 enddo do i=2,](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-14.jpg)
Zastosowanie zmiennej skalarnej do i = 2, N+1 B[i] = A[i-1]+1 enddo do i=2, N+1 C[i] =B[i] enddo do i = 2, N+1 t= A[i-1]+1 C[i] = t enddo Redukuje liczbę zapisów i odczytów elementów tablicy w pamięci operacyjnej, wartość zmiennej t może być przechowywana w rejestrze 14 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT

Rozwiń i zaciśnij (Unroll-and-Jam) for j = 1, 2*M for i = 1, N A[i, j] = A[i-1, j] + A[i-1, j-1] end_for for j = 1, 2*M, 2 for i = 1, N A[i, j]=A[i-1, j]+A[i-1, j-1] A[i, j+1]=A[i-1, j+1]+A[i-1, j] end_for Ciało drugiej pętli składa się z dwóch iteracji pierwszej pętli 15 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT

Rozwiń i zaciśnij (Unroll-and-Jam) for j = 1, 2*M for i = 1, N A[i, j] = A[i-1, j] + A[i-1, j-1] end_for for j = 1, 2*M, 2 for i = 1, N A[i, j]=A[i-1, j]+A[i-1, j-1] A[i, j+1]=A[i-1, j+1]+A[i-1, j] end_for Zwiększa lokalność przestrzenną: odwołanie do tego samego elementu 16 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT

Duże tablice Załóżmy, że tablice A i B są przechowywane kolumnami for i = 1, 1000 for j = 1, 1000 A[i, j] = A[i, j] + B[j, i] end_for Tablica A ma niską lokalność przestrzenną. Wymiana pętli nie zwiększy lokalności. Dlaczego? © Włodzimierz Bielecki, Piotr Błaszyński WI 17 ZUT

Duże tablice Załóżmy, że tablice A i B są przechowywane kolumnami for i = 1, 1000 for j = 1, 1000 A[i, j] = A[i, j] + B[j, i] end_for Wymiana pętli nie zwiększy lokalności dlatego, że nastąpi pogorszenie lokalności względem tablicy B. © Włodzimierz Bielecki, Piotr Błaszyński WI 18 ZUT

Blokowanie for v = 1, 1000, 20 for u = 1, 1000, 20 for j = v, v+19 for i = u, u+19 A[i, j] = A[i, j] + B[j, i] end_for 19 Dostęp do małych bloków macierzy zwiększa lokalność. © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT
![Rozwijanie pętliloop unroll for i 1 10 ai bi p Rozwijanie pętli(loop un-roll) for i = 1, 10 a[i] = b[i]; *p =. .](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-20.jpg)
Rozwijanie pętli(loop un-roll) for i = 1, 10 a[i] = b[i]; *p =. . . end_for i = 1, 10, 2 a[i] = b[i]; *p = … a[i+1] = b[i+1]; *p = … end_for Zwiększenie lokalności przestrzennej: odwołanie do kolejnych elementów wektorów a i b. 20 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT

Jedna metoda dla wielu transformacji Pytanie: czy istnieje metoda ujednolicenia wielu transformacji programu? 21

Jedna metoda dla wielu transformacji Pytanie: czy istnieje metoda ujednolicenia wielu transformacji programu? 22

Jedna metoda dla wielu transformacji Pytanie: czy istnieje metoda ujednolicenia wielu transformacji programu? Tak, jest to metoda transformacji afinicznych. 23

Partycjonowania afiniczne Odwzorowują w sposób jednoznaczny każdą iterację na 1. procesor/wątek lub 2. czas logiczny wykonywania iteracji lub 3. iterację w innej przestrzeni 24

Partycjonowania afiniczne Postać matematyczna: P/T/J =C*I +c, gdzie C jest macierzą, c jest wektorem; C i c określają transformacje afiniczne; P, T, J określają numer procesora, czas logiczny oraz Iterację w nowej przestrzeni. 25
![Partycjonowanie przestrzeni Ø Dla pętli niżej float Z100 for i 0 9 Zi10 Partycjonowanie przestrzeni Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-26.jpg)
Partycjonowanie przestrzeni Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] = Z[i]; end_for 1. Odwzorowanie iteracji na procesor: Procesor p wykonuje p = i iterację i, C=1, c=0 26
![Partycjonowanie czasu Ø Dla pętli niżej float Z100 for i 0 9 Zi10 Partycjonowanie czasu Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-27.jpg)
Partycjonowanie czasu Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] = Z[i]; end_for 1. Odwzorowanie iteracji na czas: t = i. Iteracja i jest wykonywana w czasie t, C=1, c=0 27
![Transformacja przestrzeni Ø Dla pętli niżej float Z100 for i 0 9 Zi10 Transformacja przestrzeni Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-28.jpg)
Transformacja przestrzeni Ø Dla pętli niżej float Z[100] for i =0, 9 Z[i+10] = Z[i]; end_for 1. Odwzorowanie iteracji na iterację w innej przestrzeni: Iteracja i jest mapowana na iterację j=2 i+1 w nowej j = 2 i+1 przestrzeni, C=2, c=1 28

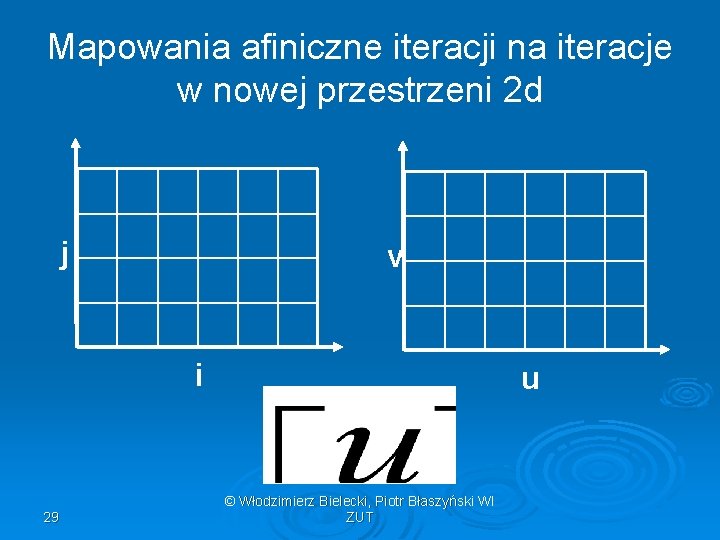
Mapowania afiniczne iteracji na iteracje w nowej przestrzeni 2 d j v i 29 u © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT

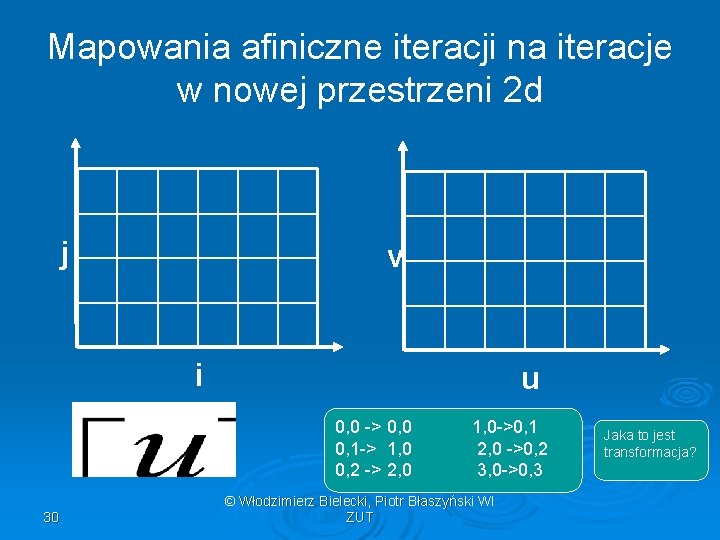
Mapowania afiniczne iteracji na iteracje w nowej przestrzeni 2 d j v i u 0, 0 -> 0, 0 0, 1 -> 1, 0 0, 2 -> 2, 0 30 1, 0 ->0, 1 2, 0 ->0, 2 3, 0 ->0, 3 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT Jaka to jest transformacja?
![Wymiana pętli for i 1 100 for j 1 200 Ai j Wymiana pętli for i = 1, 100 for j = 1, 200 A[i, j]](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-31.jpg)
Wymiana pętli for i = 1, 100 for j = 1, 200 A[i, j] = A[i, j] + 3 end_for 31 for u = 1, 200 for v = 1, 100 A[v, u] = A[v, u]+ 3 end_for © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT

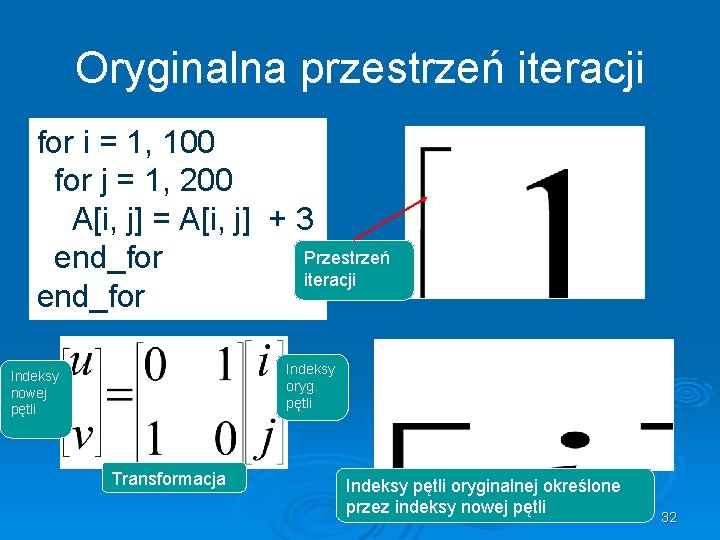
Oryginalna przestrzeń iteracji for i = 1, 100 for j = 1, 200 A[i, j] = A[i, j] + 3 Przestrzeń end_for iteracji end_for Indeksy oryg. pętli Indeksy nowej pętli Transformacja Indeksy pętli oryginalnej określone przez indeksy nowej pętli 32

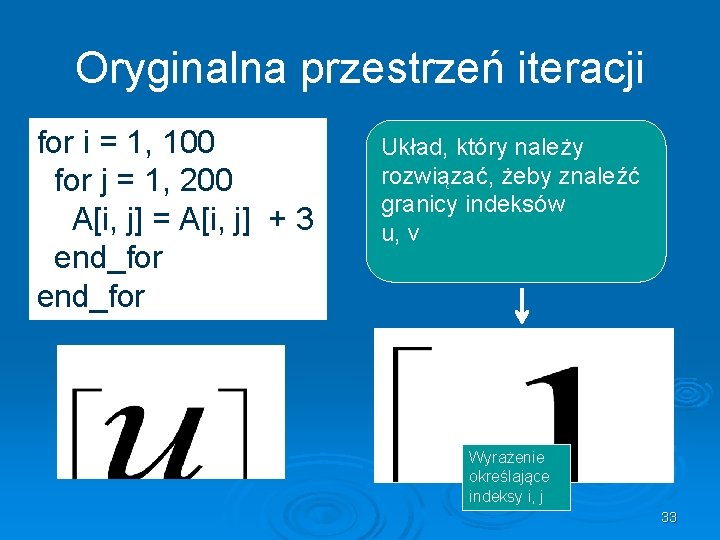
Oryginalna przestrzeń iteracji for i = 1, 100 for j = 1, 200 A[i, j] = A[i, j] + 3 end_for Układ, który należy rozwiązać, żeby znaleźć granicy indeksów u, v Wyrażenie określające indeksy i, j 33

Docelowa przestrzeń iteracji for u = 1, 200 for v = 1, 100 A[v, u] = A[v, u]+ 3 end_for Pętla docelowa end_for Rozwiązanie układu dla u, v 34

Oryginalna przestrzeń iteracji for i = 1, 100 for j = 1, 200 A[i, j] = A[i, j] + 3 end_for 35

Dostęp do A w nowej przestrzeni for u = 1, 200 for v = 1, 100 A[v, u] = A[v, u]+ 3 end_for 36 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT

Eliminacja Fouriera-Motzkina Do rozwiązania układów nierówności korzystamy z eliminacji Fouriera-Motzkina: http: //en. wikipedia. org/wiki/Fourier%E 2%80%93 Motzkin_ elimination Jean Baptiste Joseph Fourier, 1768 -1830 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 37

Eliminacja Fouriera-Motzkina THEODORE SAMUEL MOTZKIN , 1908 -1970 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 38

Eliminacja Fouriera-Motzkina JEST ZAIMPLEMENTOWANA W BIBLIOTECE : HTTP: //WEB. CSE. OHIO-STATE. EDU/~POUCHET//SOFTWARE/FM/ © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 39

Najważniejsze transformacje Podział Pętli (Loop Distribution or Loop Fission) s 1: i=p, s 2: j=p . for (p=1; p<100; p++) { s 1: a[p]= b[p]; s 2: c[p] = c[p-1] + 1; } for (i=1; i<100; i++) a[i]= b[i]; for (j=1; j<100; j++) c[j] = c[j-1] + 1; © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 40

Podział Pętli Ø Transformacja ta jest przydatna do l Zastosowania innych transformacji takich jak wymiana pętli (loop interchanging) l Zwiększenia lokalności pętli przez zmniejszenie całkowitej ilości danych, do których odwołuje każda pętla. !! Zwiększenie lokalności za pomocą tej transformacji ma miejsce, kiedy wynik produkowany przez jedną instrukcję nie jest konsumowany przez inne w tej samej iteracji. © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 41

Podział(Fission) S 1 DO I = 1, 10 S 2 DO J = 1, 10 S 3 A(I, J) = B(I, J) + C(I, J) S 4 D(I, J) = A(I, J-1) * 2. 0 S 5 ENDDO S 6 ENDDO S S 3 Loop fission (or loop distribution) dzieli pojedynczą pętle na kilka mniejszych. Ø Umożliwia wektoryzację i zrównoleglenie pod warunkiem honorowania zależności. Ø 4 S 1 DO I = 1, 10 S 2 DO J = 1, 10 S 3 A(I, J) = B(I, J) + C(I, J) Sx ENDDO Sy DO J = 1, 10 S 4 D(I, J) = A(I, J-1) * 2. 0 S 5 ENDDO S 6 ENDDO S 3 S 4 S 1 PARALLEL DO I = 1, 10 S 3 A(I, 1: 10)=B(I, 1: 10)+C(I, 1: 10) S 4 D(I, 1: 10)=A(I, 0: 9) * 2. 0 S 6 ENDDO S 3 S 4 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 42

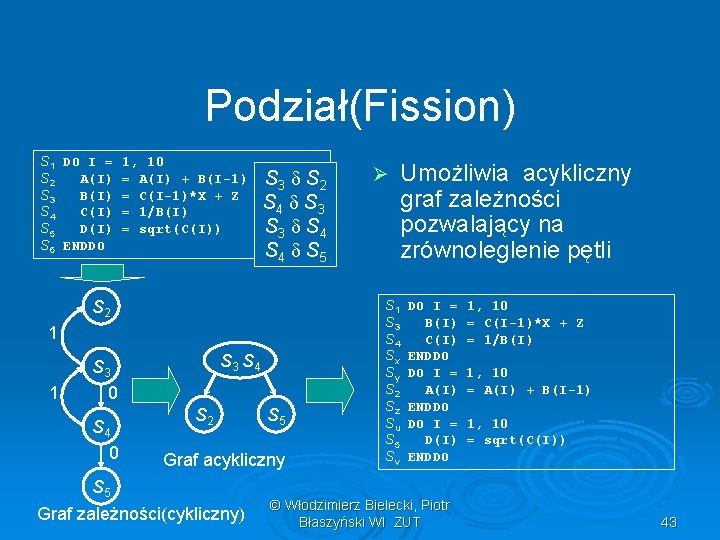
Podział(Fission) S 1 DO I = S 2 A(I) S 3 B(I) S 4 C(I) S 5 D(I) S 6 ENDDO 1, 10 = A(I) + B(I-1) = C(I-1)*X + Z = 1/B(I) = sqrt(C(I)) S 3 S 2 S 4 S 3 S 4 S 5 S 2 1 1 S 3 S 4 S 3 0 S 4 0 S 2 S 5 Graf acykliczny S 5 Graf zależności(cykliczny) Ø S 1 S 3 S 4 Sx Sy S 2 Sz Su S 5 Sv Umożliwia acykliczny graf zależności pozwalający na zrównoleglenie pętli DO I = B(I) C(I) ENDDO DO I = A(I) ENDDO DO I = D(I) ENDDO © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 1, 10 = C(I-1)*X + Z = 1/B(I) 1, 10 = A(I) + B(I-1) 1, 10 = sqrt(C(I)) 43

Scalenie Pętli (Loop Fusion) Transformacja ta scala kolejne pętle o identycznych indeksach i granicach w jedną pętlę. s 1: p=i s 2: p=j for (i=0; i<N; i++) a[i]=0; for (i=0; i<N; i++) b[i]=0; for (p=0; p<N; p++) { a[p]=0; b[p]=0; } © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 44

Scalenie Pętli Ø Transformacja l l l ta jest przydatna do Zmniejszenia czasu wykonania pętli –redukcja czasu obsługi wykonywania pętli. Zwiększenia granulacji obliczeń pętli. Poprawy lokalności poprzez odwołanie się do tej samej tablicy. © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 45
![Scalenie Pętli Przykład for i0 Bi for j0 Cj iN i fAi Scalenie Pętli Przykład: for (i=0; B[i] = for (j=0; C[j] = i<N; i++) f(A[i]);](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-46.jpg)
Scalenie Pętli Przykład: for (i=0; B[i] = for (j=0; C[j] = i<N; i++) f(A[i]); j<N; j++) f(B[j], A[j]); for (i=0; i<N; i++) B[i] = f(A[i]); C[i] = f(B[i], A[i]); lokalizacja Produkcja/Konsumpcja Lokalizacja Czas Produkcja/Konsumpcja Czas © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 46

Scalenie Pętli S 1 S 2 S 3 S 4 S 5 S 6 S 7 B(1) = DO I = B(I) ENDDO DO I = A(I) ENDDO T(1)*X(1) 2, N = T(I)*X(I) S 1 Sx S 3 S 6 Sy B(1) = DO I = B(I) A(I) ENDDO T(1)*X(1) 2, N = T(I)*X(I) S = B(I) - B(I-1) 1 Łączy dwie kolejne pętle z tymi samymi granicami w jedną pętlę. Ø Nowa pętla musi zachować wszystkie zależności pętli oryginalnej. Ø Umożliwia optymalizacje skalarne pętli. Ø Ale: może zmniejszyć lokalność czasową. Ø 2, N = B(I) - B(I-1) S 1 S 6 S 3 S 6 Zależności pętli oryginalnej S 1 S 6 , S 3 S 6 Zależności pętli po transformacji S 1 S 6 and S 3 S 6 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 47

Przykład S 1 S 2 S 3 S 4 S 5 S 6 S 7 S 8 S 9 DO I = A(I) ENDDO DO I = C(I) ENDDO DO I = D(I) ENDDO a) S 1 S 2 S 3 Sx S 5 S 8 Sy DO I = A(I) ENDDO DO I = C(I) D(I) ENDDO Sx S 2 S 5 Sy S 7 S 8 S 9 DO I = A(I) C(I) ENDDO DO I = D(I) ENDDO 1, N = B(I) + 1 = A(I)/2 Sx S 2 S 5 S 8 © Włodzimierz Bielecki, Piotr Błaszyński WI Sy ZUT DO I = A(I) C(I) D(I) ENDDO 1, N = B(I) + 1 = A(I)/2 = 1/C(I) 1, N = B(I) + 1 1, N = A(I)/2 1, N = 1/C(I) b) Które z tych trzech scalonych pętli są legalne? c) 1, N = B(I) + 1 1, N = A(I)/2 = 1/C(I) 1, N = 1/C(I) 48

Przykład S 1 S 2 S 3 S 4 S 5 S 6 S 7 S 8 S 9 DO I = A(I) ENDDO DO I = C(I) ENDDO DO I = D(I) ENDDO 1, N = B(I) + 1 a) 1, N = A(I)/2 1, N = 1/C(I) Każda z tych trzech scalonych pętli jest legalna ponieważ wszystkie zależności są honorowane b) S 1 S 2 S 3 Sx S 5 S 8 Sy DO I = A(I) ENDDO DO I = C(I) D(I) ENDDO Sx S 2 S 5 Sy S 7 S 8 S 9 DO I = A(I) C(I) ENDDO DO I = D(I) ENDDO 1, N = B(I) + 1 1, N = A(I)/2 = 1/C(I) 1, N = B(I) + 1 = A(I)/2 1, N = 1/C(I) c) Sx DO I = 1, N S 2 A(I) = B(I) + 1 S 5 C(I) = A(I)/2 S 8 D(I) = 1/C(I) © Włodzimierz Bielecki, Piotr Błaszyński WI Sy ENDDO ZUT 49

Wymiana Pętli (Loop Interchanging) Ø Transformacja ta wymienia pętle miejscami i’=j j’=i for (i=0; i<M; i++) for (j=0; j<N; j++) A[i, j]=0. 0; for (j=0; j<M; j++) for (i=0; i<N; i++) A[i, j]=0. 0; © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 50

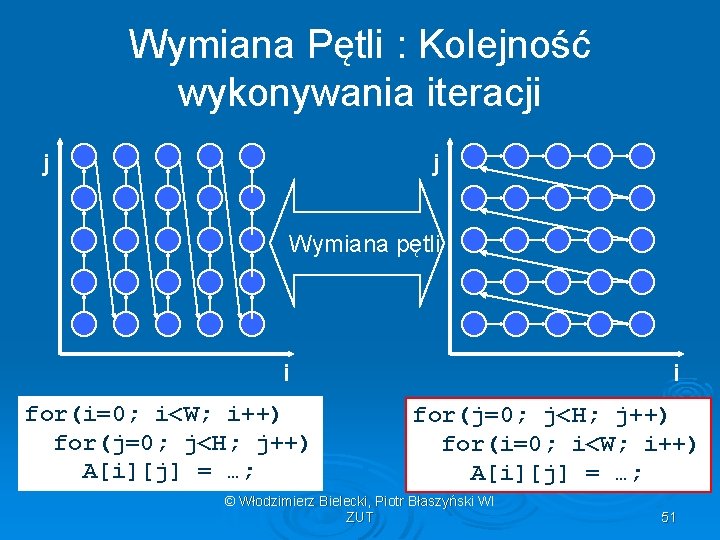
Wymiana Pętli : Kolejność wykonywania iteracji j j Wymiana pętli i for(i=0; i<W; i++) for(j=0; j<H; j++) A[i][j] = …; i for(j=0; j<H; j++) for(i=0; i<W; i++) A[i][j] = …; © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 51

Wymiana Pętli Często stosowana jest w celu zwiększenia lokalności przestrzennej – dopasowanie do sposobu przechowywania elementów tablic(wierszami lub kolumnami). Może zmniejszyć czas wykonania pętli nawet do 10 razy. © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 52

Przykład S 1 DO I = 1, N S 2 DO J = 1, M S 3 A(I, J) = A(I, J-1) + B(I, J) S 4 ENDDO S 5 ENDDO S S 3 3 S 2 DO J = 1, M S 1 DO I = 1, N S 3 A(I, J) = A(I, J-1) + B(I, J) S 4 ENDDO S 5 ENDDO S S 3 Ø 3 Transformacja wymiany pętli musi zachować wszystkie zależności oryginalnej pętli. Pozwala zwiększyć lokalność Ø Umożliwia wektoryzację Ø S 2 DO J = 1, M S 3 A(1: N, J)=A(1: N, J-1)+B(1: N, J) S 5 ENDDO S 3 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 53
![Odwrócenie iteracji pętli Loop Reversal Ø pNi for i0 iN i aibi1 ciai2 Odwrócenie iteracji pętli (Loop Reversal) Ø p=N-i for (i=0; i<N; i++){ a[i]=b[i]+1; c[i]=a[i]/2; }](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-54.jpg)
Odwrócenie iteracji pętli (Loop Reversal) Ø p=N-i for (i=0; i<N; i++){ a[i]=b[i]+1; c[i]=a[i]/2; } for (i=N-1; i<=0; i--){ a[i]=b[i]+1; c[i]=a[i]/2; } © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 54
![Odwrócenie iteracji pętli może zwiększyć lokalność for i0 iN i for Bi I Odwrócenie iteracji pętli może zwiększyć lokalność for (i=0; i<=N; i++) for. B[i] I =](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-55.jpg)
Odwrócenie iteracji pętli może zwiększyć lokalność for (i=0; i<=N; i++) for. B[i] I = exp 1 to exp 2 = f(A[i]); for (i=0; A(I)i<=N; i++) C[i] = g(B[N-i]); Produkcja konsumpcja czas for (i=0; i<=N; i++) for. B[i] I = exp 2 downto exp 1 = f(A[i]); for (i=N; A(I)i<=0; i--) C[N-i] = g(B[(N-i)]); Iteracje są wykonywane w odwrotnej kolejności © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT czas 55

Przekoszenie iteracji pętli (Loop Skew) Transformacja: p 1=i-j p 2=j+1 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 56

Przekoszenie iteracji pętli j j Przekoszenie i i for(j=0; j<H; j++) for(i=0; i<W; i++) A[i][j] =. . . ; for(j=0; j<H; j++) for(i=0+j; i<W+j; i++) A[i-j][j] =. . . ; © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 57
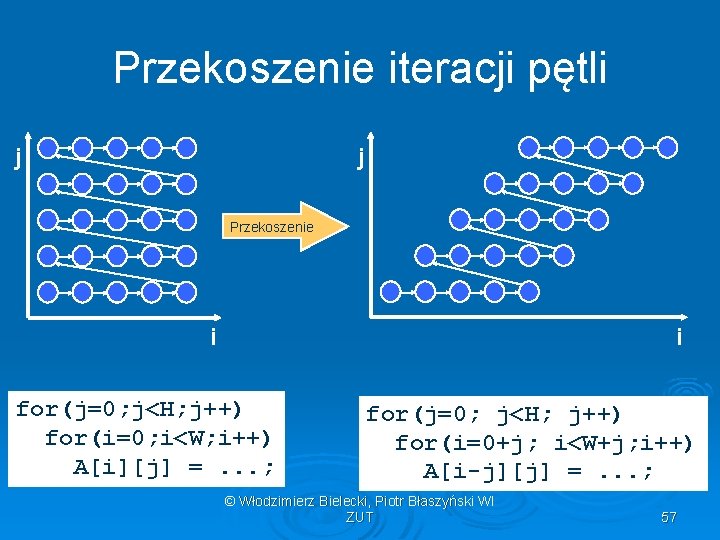
![for i0 iN i for j0 jM j Ai1j fAij1 i Prz eko for (i=0; i<N; i++) for (j=0; j<M; j++) A[i+1][j] = f(A[i][j+1]); i Prz eko](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-58.jpg)
for (i=0; i<N; i++) for (j=0; j<M; j++) A[i+1][j] = f(A[i][j+1]); i Prz eko sze nie i j ętli m Wy p ana i j j Loop skewing pozwala na wymianę pętli i 58
![Blokowanie1 D i Blokowanie 1 D j i fori0 i9 i Ai Blokowanie(1 -D ) i Blokowanie 1 -D j i for(i=0; i<9; i++) A[i] =.](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-59.jpg)
Blokowanie(1 -D ) i Blokowanie 1 -D j i for(i=0; i<9; i++) A[i] =. . . ; for(j=0; j<3; j++) for(i=4*j; i<4*j+4; i++) if (i<9) A[i] =. . . ; © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 59

Blokowanie (Loop Blocking or Tiling) Ø Poprawia lokalność kodu Ø Użyteczne tylko gdy rozmiar wszystkich danych programu jest większy od rozmiaru pamięci podręcznej. © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 60
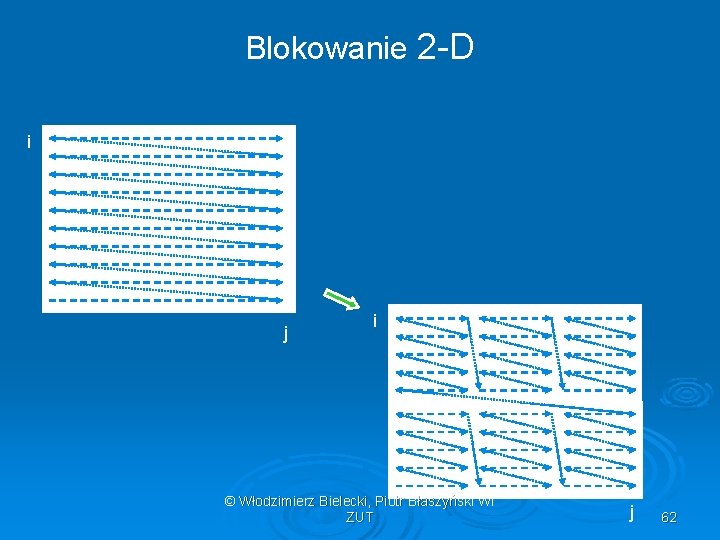
![Blokowanie 2 D fori0 iN i forj0 jN j Aij Bji forTI0 TIN Blokowanie 2 -D for(i=0; i<N; i++) for(j=0; j<N; j++) A[i][j] = B[j][i]; for(TI=0; TI<N;](https://slidetodoc.com/presentation_image_h2/1b65e5cf3806f05400c89069aa95f2b7/image-61.jpg)
Blokowanie 2 -D for(i=0; i<N; i++) for(j=0; j<N; j++) A[i][j] = B[j][i]; for(TI=0; TI<N; TI+=16) for(TJ=0; TJ<N; TJ+=16) for(i=TI; i<min(TI+16, N); i++) Inside for(j=TJ; j<min(TJ+16, N); j++) a tile = B[j][i]; © Włodzimierz. A[i][j] Bielecki, Piotr Błaszyński WI ZUT 61

Blokowanie 2 -D i j i © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT j 62

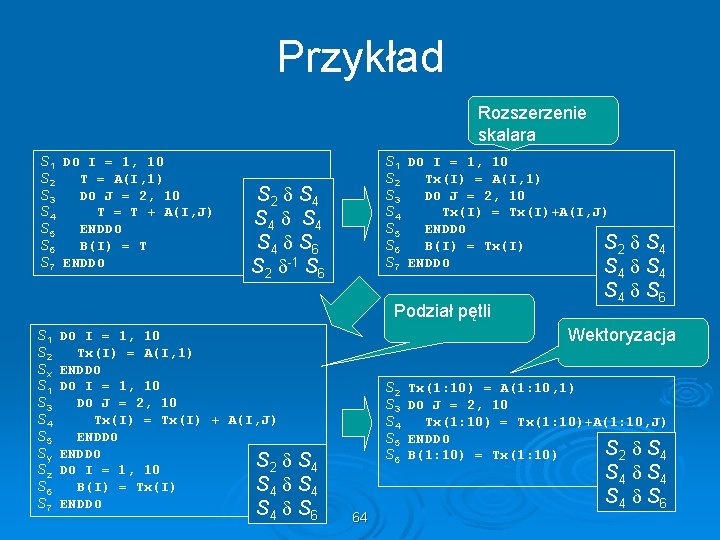
Rozszerzenie skalara S 1 DO I = 1, N S 2 T = A(I) + B(I) S 3 C(I) = T + 1/T S 4 ENDDO S 2 S 3 S 2 -1 S 3 Sx IF N > 0 THEN Sy ALLOC Tx(1: N) S 1 DO I = 1, N S 2 Tx(I) = A(I) + B(I) Sx C(I) = Tx(I) + 1/Tx(I) S 4 ENDDO Sz T = Tx(N) Su ENDIF S 2 S 3 Usuwa zależności odwrotne poprzez rozszerzenie zmiennej skalarnej do tablicy. Ø Zależności odwrotne uniemożliwiają niektóre transformacje pętli takie jak podział pętli i wymiany pętli. Ø © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 63

Przykład Rozszerzenie skalara S 1 DO I = 1, 10 S 2 T = A(I, 1) S 3 DO J = 2, 10 S 4 T = T + A(I, J) S 5 ENDDO S 6 B(I) = T S 7 ENDDO S 1 DO I = 1, 10 S 2 Tx(I) = A(I, 1) S 3 DO J = 2, 10 S 4 Tx(I) = Tx(I)+A(I, J) S 5 ENDDO S 2 S 6 B(I) = Tx(I) S 7 ENDDO S S 2 S 4 S 4 S 6 S 2 -1 S 6 Podział pętli S 1 S 2 Sx S 1 S 3 S 4 S 5 Sy Sz S 6 S 7 DO I = 1, 10 Tx(I) = A(I, 1) ENDDO DO I = 1, 10 DO J = 2, 10 Tx(I) = Tx(I) + A(I, J) ENDDO S 2 DO I = 1, 10 S 4 B(I) = Tx(I) ENDDO S 4 S 4 S 6 S 4 4 S 6 Wektoryzacja S 2 S 3 S 4 S 5 S 6 64 Tx(1: 10) = A(1: 10, 1) DO J = 2, 10 Tx(1: 10) = Tx(1: 10)+A(1: 10, J) ENDDO S 2 S 4 B(1: 10) = Tx(1: 10) S 4 S 4 S 6

Dziękuję za uwagę © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 65
 Transformacje galileusza
Transformacje galileusza Podstawowe instrukcje
Podstawowe instrukcje Elementy zestawu komputerowego
Elementy zestawu komputerowego Podstawowe manewry na drodze prezentacja
Podstawowe manewry na drodze prezentacja Podstawowe zwroty po ukraińsku
Podstawowe zwroty po ukraińsku Największe państwa
Największe państwa Dopisz wyrazy podstawowe i pochodne według wzoru
Dopisz wyrazy podstawowe i pochodne według wzoru Transformacja encji
Transformacja encji Podstawowe figury geometryczne
Podstawowe figury geometryczne Jak zastawić stół
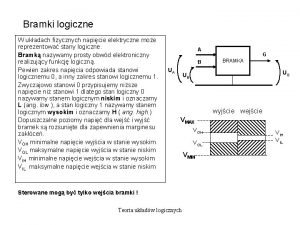
Jak zastawić stół Symbole bramek logicznych
Symbole bramek logicznych Pojęcia światła oraz barwy. podstawowe modele barw.
Pojęcia światła oraz barwy. podstawowe modele barw. Komunikacja jednokierunkowa
Komunikacja jednokierunkowa Kroki fitness choreografia
Kroki fitness choreografia Colormap matlab
Colormap matlab Druk minibaru
Druk minibaru Www.platforma.wint.pl
Www.platforma.wint.pl ściąganie plików
ściąganie plików Podstawowe gałęzie transportu
Podstawowe gałęzie transportu Podstawowe usługi internetowe
Podstawowe usługi internetowe Podstawowe informacje o biblii
Podstawowe informacje o biblii Ceramiczna zastawa stołowa przykłady
Ceramiczna zastawa stołowa przykłady Substancje wzorcowe w alkacymetrii
Substancje wzorcowe w alkacymetrii Elementy podstawowego zestawu komputerowego
Elementy podstawowego zestawu komputerowego Wielkość fizyczna jednostki i pomiary
Wielkość fizyczna jednostki i pomiary Zasady netykiety
Zasady netykiety Platforma edukacyjna osp odpowiedzi
Platforma edukacyjna osp odpowiedzi Figura wklęsła
Figura wklęsła Emocje podstawowe
Emocje podstawowe Usos pśk
Usos pśk Podstawowe tożsamości trygonometryczne
Podstawowe tożsamości trygonometryczne