Kompilatory Optymalizujce Wykad 6 1 godz Tranzytywne domknicie

Kompilatory Optymalizujące Wykład 6, 1 godz. Tranzytywne domknięcie, pojęcie, algorytmy obliczania © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 1

Plan Definicja tranzytywnego domknięcia 2. Sposoby obliczenia tranzytywnego domknięcia 1. © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 2

Potęga relacji Przykład: R={[i, j]->[i, j+1]: 0<=i<=3 && 0<=j<=2}; R 1 = R = {[i, j]->[i, j+1]: 0<=i<=3 && 0<=j<=2}; R 2 = R R = {[i, j] -> [i, j+2] : 0 <= i <= 3 && 0 <= j <= 1}; R 3 = R R R= {[i, 0] -> [i, 3] : 0 <= i <= 3}; R 4= R R= zbór pusty ………. Rn+1 = Rn R = zbór pusty 3

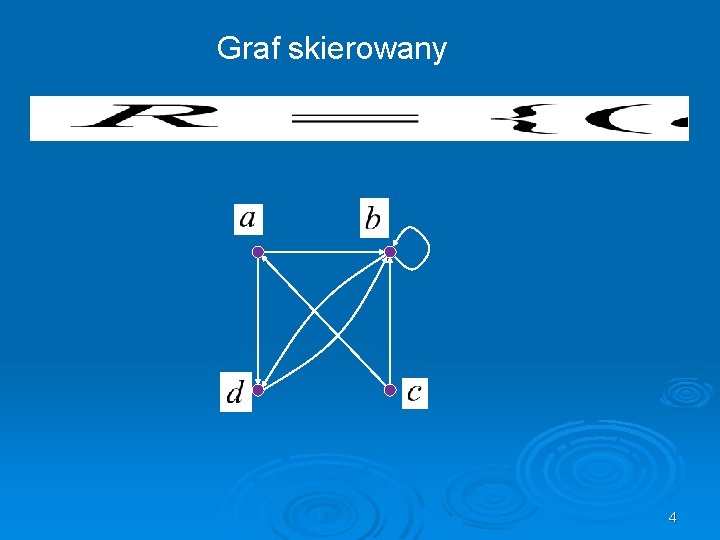
Graf skierowany 4

Relacja jako reprezentacja grafu zależności Przykład: R : = {[i, j] -> [i, j+1] : 1 <= i <= 4 && 1 <= j <= 3} j 4 3 2 1 j 1 2 3 Graf zależności jest skierowany: ruch po grafie możliwy jest tylko w kierunkach wskazywanych przez krawędzie. 4 © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 5

Tranzytywne domkniecie Niech G = (V, A) będzie grafem skierowanym, gdzie V jest to zbiór węzłów, A jest to zbiór krawędzi. Graf skierowany G+ = (V, A+) nazywany jest domknięciem przechodnim (tranzytywnym) grafu G, gdy A+ jest zbiorem wszystkich takich par (a, b) wierzchołków ze zbioru V, że w grafie G istnieje droga z a do b. © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 6

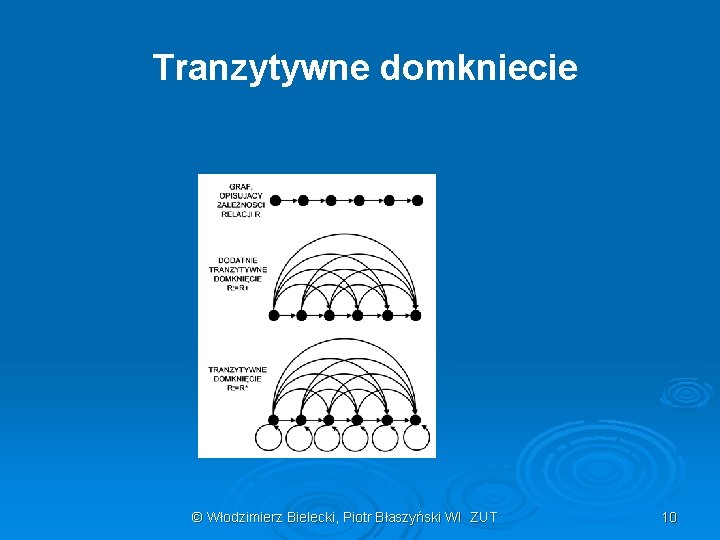
Tranzytywne domkniecie Prościej mówiąc, tranzytywne domkniecie określa dla każdego węzła grafu wszystkie węzły, połączone z danym węzłem pośrednią lub bezpośrednią ścieżką skierowaną. Bezpośrednia ścieżka ma długość 1, natomiast długość ścieżki pośredniej jest większa od 1. © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 7

Pozytywne tranzytywne domkniecie Pozytywne tranzytywne domknięcie relacji R, R+, obliczamy jako: R+= R R 2 R 3 . . .

Tranzytywne domkniecie Tranzytywne domknięcie relacji R, R*, obliczamy jako: R *= I R + gdzie I jest relacją tożsamości, która mapuje każdy element krotki wejściowej na ten sam element krotki wyjściowej: {[i, j]->[i, j]: brak ograniczeń}.

Tranzytywne domkniecie © Włodzimierz Bielecki, Piotr Błaszyński WI ZUT 10

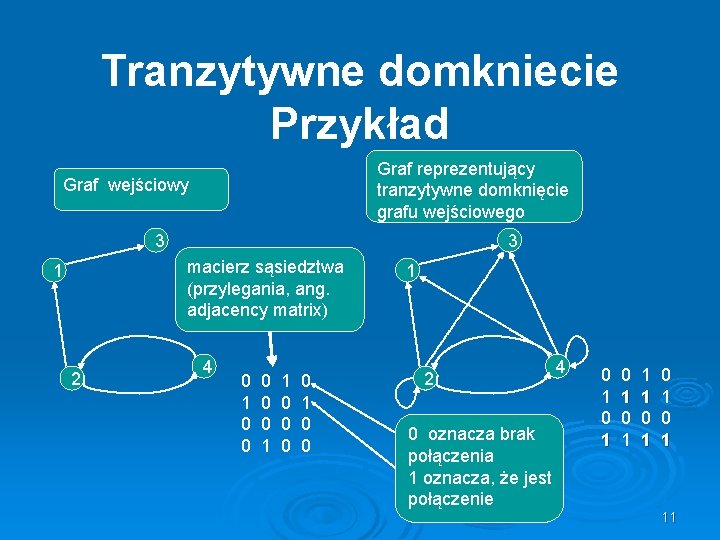
Tranzytywne domkniecie Przykład Graf reprezentujący tranzytywne domknięcie grafu wejściowego Graf wejściowy 3 3 macierz sąsiedztwa (przylegania, ang. adjacency matrix) 1 2 4 0 1 0 0 0 1 1 0 0 1 2 0 oznacza brak połączenia 1 oznacza, że jest połączenie 4 0 1 0 1 1 1 0 1 0 1 11

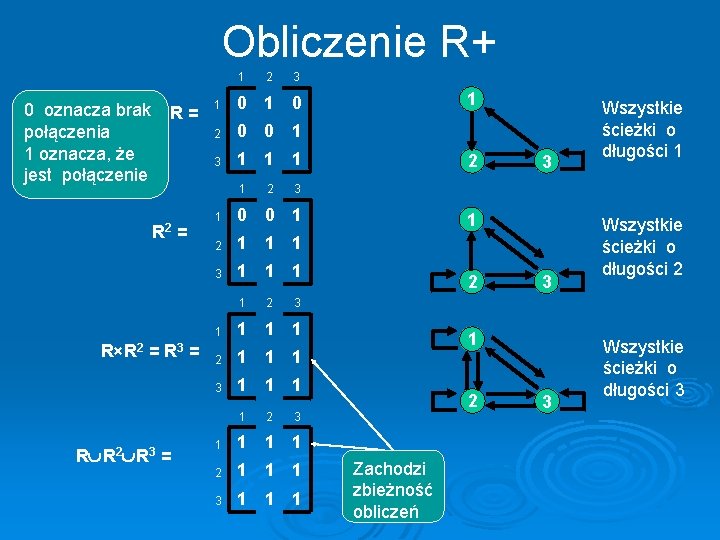
Obliczenie R+ 1 0 oznacza brak połączenia 1 oznacza, że jest połączenie R= = 0 1 0 2 0 0 1 3 1 1 1 2 1 1 1 3 1 1 1 2 2 3 Wszystkie ścieżki o długości 1 1 2 3 Wszystkie ścieżki o długości 2 3 1 1 2 1 1 1 3 1 1 1 2 1 3 0 0 1 1 R R 2 R 3 = 2 1 1 R×R 2 = R 3 = 3 1 1 R 2 2 1 2 3 1 1 2 1 1 1 3 1 1 1 Zachodzi zbieżność obliczeń 3 Wszystkie ścieżki o długości 3

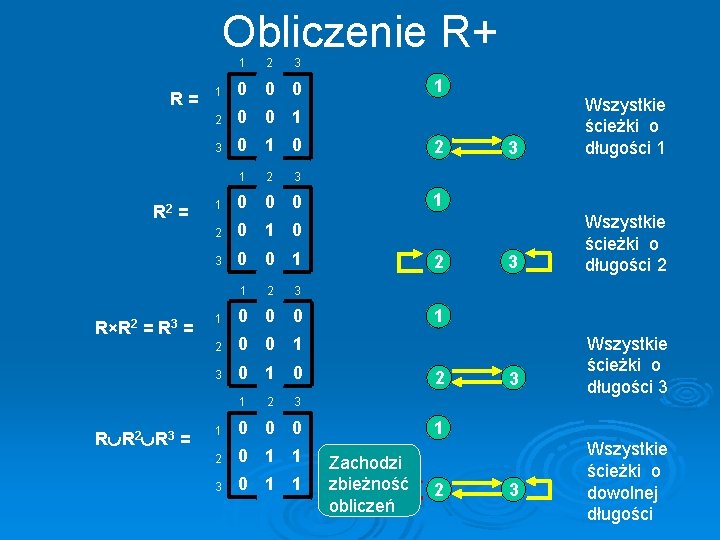
Obliczenie R+ 1 R= 0 0 0 2 0 0 1 3 0 1 0 2 0 1 0 3 0 0 1 2 2 3 Wszystkie ścieżki o długości 1 3 Wszystkie ścieżki o długości 2 3 Wszystkie ścieżki o długości 3 1 2 3 1 0 0 0 2 0 0 1 3 0 1 0 2 1 3 0 0 0 1 R R 2 R 3 = 2 1 1 R×R 2 = R 3 = 3 1 1 R 2 = 2 1 2 3 1 0 0 0 2 0 1 1 3 0 1 1 1 Zachodzi zbieżność obliczeń 2 3 Wszystkie ścieżki o dowolnej długości

Obliczenie R+ Zbieżność obliczeń R+ jest gwarantowana tylko dla grafów, których liczba węzłów jest skończona. Dla pętli sparametryzowanych, liczba węzłów w grafie zależności jest nieokreślona (sparametryzowana). Dla takich grafów w celu obliczenia R+ można zastosować algorytm Floyda-Warshalla. 14

Algorytm Floyda-Warshalla Idea: ścieżka istnieje między węzłami i, j wtedy gdy Istnieje krawędź od i do j lub Istnieje ścieżka od i do j, przechodząca przez węzeł 1; lub Istnieje ścieżka od i do j, przechodząca przez węzeł 1 i/lub 2; lub • … Istnieje ścieżka od i do j, przechodząca przez węzeł • 1, 2, … i/lub k; lub • . . . Istnieje ścieżka od i do j, przechodząca przez każdy z pozostałych węzłów. 15 15

Algorytm Floyda-Warshalla Transitive-Closure(W[1. . n]) W jest macierzą sąsiedztwa 01 T ¬ W // T(0) 02 for k ¬ 1 to n do // compute T(k) 03 for i ¬ 1 to n do 04 for j ¬ 1 to n do 05 T[i][j] ¬ T[i][j] Ú (T[i][k] Ù T[k][j]) 06 return T Każda iteracja względem k buduje ścieżki uwzględniając wyniki poprzednich rund. Po iteracjach dotyczących wszystkich wierzchołków pośrednich k, dostajemy połączenia wszystkich par wierzchołków i oraz j przez wszystkie wierzchołki pośrednie k.

Algorytm Floyda-Warshalla Transitive-Closure(W[1. . n]) W jest macierzą sąsiedztwa 01 T ¬ W // T(0) 02 for k ¬ 1 to n do // compute T(k) 03 for i ¬ 1 to n do 04 for j ¬ 1 to n do 05 T[i][j] ¬ T[i][j] Ú (T[i][k] Ù T[k][j]) 06 return T Jest możliwy do zastosowania tylko dla grafów, których liczba węzłów jest skończona.

Modyfikacja Algorytmu Floyda -Warshalla Algorytm jest modyfikowany ponieważ nie tylko decyduje o istnieniu krawędzi ale również charakteryzuje ją. Na wejściu dostaje graf, którego węzły reprezentują instrukcje pętli. W iteracji k, aktualizuje wszystkie zależności, żeby uwzględnić wszystkie zależności tranzytywne powodowane instrukcjami pętli od 1 do k. Podstawowym wyrażeniem algorytmu jest Ono zawiera wyrażenie ponieważ chcemy uwzględnić następujące zależności: 18 18

Algorytm Floyda-Warshalla Jeśli istnieje: 1) zależność od iteracji i 1 instrukcji Sp do iteracji i 2 instrukcji Sr oraz 2) łańcuch samo zależności od iteracji i 2 do iteracji i 3 instrukcji Sr oraz 3) zależność od iteracji 3 instrukcji Sr do iteracji i 4 instrukcji Sq, to istnieje samo zależność tranzytywna od iteracji i 1 do iteracji i 4. 19 19

Algorytm Floyda-Warshalla Samo zależność (self dependence) oznacza, że zależności są powodowane różnymi instancjami tej samej instrukcji. i 1 Sp 20 i 3 i 2 Sr i 4 Sq 1) zależność od iteracji i 1 instrukcji Sp do iteracji i 2 instrukcji Sr oraz 2) łańcuch samo zależności od iteracji i 2 do iteracji i 3 instrukcji Sr oraz 3) zależność od iteracji 3 instrukcji Sr do iteracji i 4 instrukcji Sq, 20

Algorytm Floyda-Warshalla Powinniśmy skorzystać z jakiegoś algorytmu do obliczenia D*kk 21 Szczegóły są w artykule: Bielecki, W. , et. al. : Using basis dependence distance vectors to calculate the transitive closure of dependence relations by means of the Floyd-Warshall algorithm. In: Journal of Combinatorial Optimization (2014). 21

Bibliografia Kelly, W. , Pugh, W. , Rosser, E. , & Shpeisman, T. (1996). Transitive closure of infinite graphs and its applications. International Journal of Parallel Programming, 24(6), 579 -598. 22

Bibliografia BIELECKI, Wlodzimierz; KLIMEK, Tomasz; TRIFUNOVIC, Konrad. Calculating exact transitive closure for a normalized affine integer tuple relation. Electronic Notes in Discrete Mathematics, 2009, 33: 7 -14. Beletska, A. , Barthou, D. , Bielecki, W. , & Cohen, A. (2009, June). Computing the transitive closure of a union of affine integer tuple relations. In International Conference on Combinatorial Optimization and Applications (pp. 98 -109). Springer, Berlin, Heidelberg. WLODZIMIERZ, Bielecki, et al. An iterative algorithm of computing the transitive closure of a union of parameterized affine integer tuple relations. In: International Conference on Combinatorial Optimization and Applications. Springer, Berlin, Heidelberg, 2010. p. 104 -113. 23

Bibliografia Bielecki, W. , Kraska, K. , & Klimek, T. (2013, September). Transitive closure of a union of dependence relations for parameterized perfectly-nested loops. In International Conference on Parallel Computing Technologies (pp. 37 -50). Springer, Berlin, Heidelberg. Bielecki, W. , Klimek, T. , & Pietrasik, M. (2009). Obliczenie tranzytywnego domknięcia sparametryzowanych relacji zależności nie należących do klasy d-form. Metody Informatyki Stosowanej, (2 (19)), 5 -15. Bielecki, W. , Klimek, T. , Palkowski, M. , & Beletska, A. (2012). An Iterative Algorithm of Computing the Transitive Closure of a Union of Parametrized Affine Integer Tuple Relations. Discrete Mathematics, Algorithms and Applications, 4(01), 1250011. 24

Bibliografia BIELECKI, Włodzimierz; KLIMEK, Tomasz. Zwiększenie zbieżności iteracyjnego algorytmu obliczania tranzytywnego domknięcia unii sparametryzowanych relacji zależności. Metody Informatyki Stosowanej, 2010, 2 (23): 3747. VERDOOLAEGE, Sven; COHEN, Albert; BELETSKA, Anna. Transitive closures of affine integer tuple relations and their overapproximations. In: International Static Analysis Symposium. Springer, Berlin, Heidelberg, 2011. p. 216 -232. 25

Dziękuję za uwagę 26