Teora de Nmeros Dra Noem L Ruiz Limardo




































- Slides: 37

Teoría de Números Dra. Noemí L. Ruiz Limardo Revisado 2011 © Derechos de Autor Reservados

Objetivos 1. Conocer las definiciones básicas relacionadas con factorización 2. Hallar la factorización prima de un número 3. Conocer el significado de MCM y MFC 4. Usar la factorización prima para hallar el MCM y MFC 5. Hallar el MCM y MFC de números dados.

Factores Números que se multiplican para obtener un producto Ejemplos de factores de 12: 12 y 1 ya que 12. 1 = 12 3 y 4 ya que 3. 4 = 12 6 y 2 ya que 6. 2 = 12 Factores de 12: 12, 1, 6, 2, 4, 3

Número Primo Número natural mayor que 1 cuyos únicos factores son él mismo y 1. Ejemplo de números primos: 2 , 3, 5 Menciona otros

Conjunto de los Números Primos { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …} Observa que: • El conjunto es infinito. • El número primo menor es 2. • El único número primo que es par es 2, los demás son impares. • No todos los impares son primos, por ejemplo, el 9 es impar pero no es primo. • Ver lista de números primos hasta el 100

Número Compuesto Número natural que no es primo, o sea, tiene otros factores además de él mismo y uno. Ejemplo de números compuestos: 4 , 9, 15, 64 Menciona otros

Exponentes y Potencias Una potencia es cuando tenemos un número (base) elevado a un exponente. Ejemplo: 32 Significa que se multiplica la base tantas veces 43 como diga el exponente.

Exponentes y Potencias Una potencia es cuando tenemos un número llamado base) elevado a un exponente. Significa que se multiplica la base tantas veces como diga el exponente Ejemplo: 32 = 3 x 3 = 9 43 = 4 x 4 = 64

Factorización. . . Proceso mediante el cual se descompone un número como el producto (multiplicación) de dos o más números. Ejemplo: 10 = 5. 2 12 = 4. 3

Factorización prima. . . Proceso mediante el cual se descompone un número como el producto (multiplicación) de dos o más números primos. Ejemplo: 7 = 7. 1 6 = 2. 3

Teorema Fundamental de la Aritmética. . . Todo número natural compuesto puede expresarse de una forma única, como un producto de factores primos.

Divisibilidad. . . Un número a es divisible por b, si al dividir a por b se obtiene un número entero. Ejemplo: 10 es divisible por 2 ya que al dividir 10 por 2 se obtiene el entero 5.

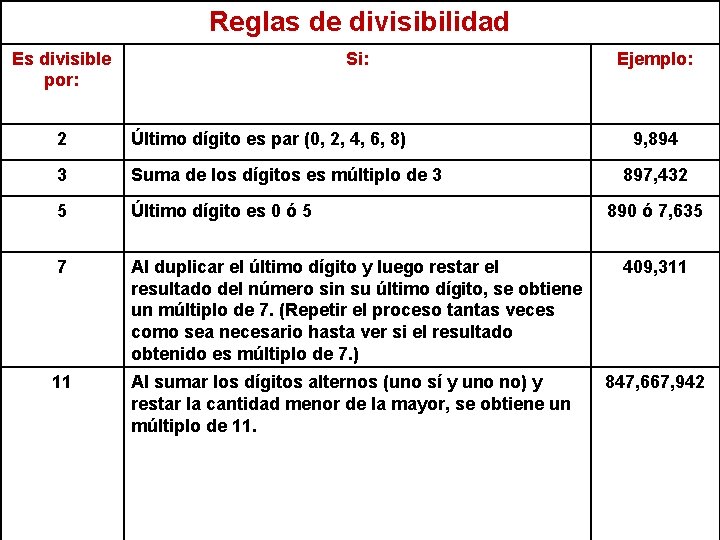
Reglas de divisibilidad Es divisible por: Si: 2 Último dígito es par (0, 2, 4, 6, 8) 3 Suma de los dígitos es múltiplo de 3 5 Último dígito es 0 ó 5 7 Al duplicar el último dígito y luego restar el resultado del número sin su último dígito, se obtiene un múltiplo de 7. (Repetir el proceso tantas veces como sea necesario hasta ver si el resultado obtenido es múltiplo de 7. ) 11 Al sumar los dígitos alternos (uno sí y uno no) y restar la cantidad menor de la mayor, se obtiene un múltiplo de 11. Ejemplo: 9, 894 897, 432 890 ó 7, 635 409, 311 847, 667, 942

Ejercicios de práctica para determinar cuando un número es divisible por 2, 3, 5, 7, y 11.

Determina si los números son divisibles por 2, 3, 5, 7, 11 315 Más ejemplos en 630 próxima pantalla. 45, 815 123, 456, 789 987, 654, 321 142, 891 409, 311

Determina si los números son divisibles por 2, 3, 5, 7, 11 409, 311 458, 485 287, 824 8, 493, 969 847, 667, 942 453, 896, 248 552, 749, 913

Factorización Prima de un Número

Método del árbol para hallar la factorización prima de un número • Se buscan dos factores cualesquiera del número que se va a factorizar y se colocan como dos ramas del árbol. • Si el factor es un número primo, la rama del árbol termina. Continúa en próxima pantalla.

Método del árbol para hallar la factorización prima de un número • Si el factor no es primo, se buscan dos factores cualesquiera y se colocan como dos ramas del árbol bajo la ramificación anterior. • El proceso continúa hasta que se obtienen números primos en todas las ramas del árbol. • Ver proceso en las próximas pantallas.

Método del árbol de factorización • Halla la factorización prima de 63 63 3 3 y 21 son dos factores cualesquiera de 63 21 3 7 Como el 3 es primo, termina la rama, como el 21 no es primo continúa ramificándose el árbol Termina el proceso cuando se obtienen ramas que tiene solo números primos La factorización prima de 63 es: 32. 7 Los factores primos que están repetidos se expresan en potencias

Método del árbol de factorización • Hallar la factorización prima de 504 2 252 2 126 2 63 3 21 3 7 La factorización prima de 504 es: 2 3. 32. 7

Ejercicios de práctica

Halla la factorización prima de los siguientes números 240 300 360 425 663 885

MCD y MCM

Proceso para hallar el Máximo Factor Común (MFC) (o Máximo Común Divisor-MCD) de dos o más números • Halla la factorización prima de cada número. • Expresa los factores que se repiten como una potencia. • Determina los factores que son comunes a todos los números. • Selecciona, de los factores comunes, las potencias menores. • Multiplica todos los factores obtenidos en el paso anterior.

Ejemplo: Hallar el MFC de 360 y 2700 • La factorización prima de cada uno, expresado como potencias de factores es: 360 = 23. 32. 5 2700 = 22. 33. 52 • Los factores comunes son: 2, 3, 5 • Selecciona las potencias menores de cada uno: 2 2. 32. 5 • Multiplicando todo tenemos que MFC = 22. 32. 5 = 180

Proceso para hallar el Mínimo Común Múltiplo (MCM) de dos o más números • Halla la factorización prima de cada número. • Expresa los factores que se repiten como una potencia. • Determina los factores que son comunes a todos los números. • Selecciona, de los factores comunes, las potencias mayores. • Selecciona todos los demás factores (los que no fueron comunes) • Multiplica todos los factores obtenidos en los dos últimos pasos.

Ejemplo: Hallar el MCM de 135, 280, y 300 • La factorización prima de cada uno, expresado como potencias de factores es: 135 = 33. 5 280 = 23. 5. 7 300 = 22. 3. 52 • De los factores comunes selecciona las potencias mayores: 2 3. 33. 52 • Los factores no comunes son: 7 • Multiplicando todo tenemos que MFC = 23. 33. 52. 7 = 37, 800

Ejercicios de práctica

Halla el MFC de los números a continuación 70 y 120 Más ejemplos en 180 y 300 próxima pantalla. 480 y 1800 168 y 504 28, 35 y 56 252, 308 y 504

Halla el MCM de los números a continuación 24 y 32 35 y 56 45 y 75 48, 54 y 60 16, 120 y 216

¿Para qué o cuándo se usa el MFC?

Se usa el MFC. . . § Uno de los usos más importantes es cuando se simplifica una fracción § En este caso se halla el MFC del numerador y el denominador y se divide ambos por esta cantidad.

¿Para qué o cuándo se usa el MCM?

Se usa el MCM. . . § Uno de los usos más importantes es cuando se suman fracciones con denominadores diferentes. § Cuando se busca un denominador común a dos o más fracciones lo que se busca es el MCM de los denominadores.

Fin de la Lección

Números Primos hasta 100 { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, . . . }
 Dra. lucila esmeralda ruiz jáuregui
Dra. lucila esmeralda ruiz jáuregui La teora
La teora Camina con noem
Camina con noem 1noem drie voorbeelden van assimilatieproducten.
1noem drie voorbeelden van assimilatieproducten. Zoolganger
Zoolganger Thermolyse van suiker
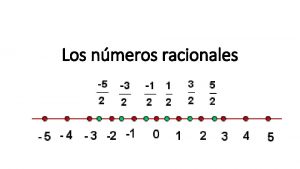
Thermolyse van suiker Nmeros reales
Nmeros reales Nmeros romanos
Nmeros romanos Nmeros ordinales
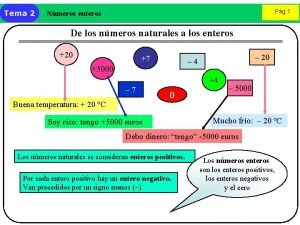
Nmeros ordinales Nmeros enteros
Nmeros enteros Nmeros naturales
Nmeros naturales Los nmeros
Los nmeros Primero, segundo, tercero, cuarto
Primero, segundo, tercero, cuarto Nmeros enteros
Nmeros enteros Ivx número romano
Ivx número romano Número divisivel por 7
Número divisivel por 7 Nmeros naturales
Nmeros naturales 142 en numeros romanos
142 en numeros romanos Temporalidad de los romanos
Temporalidad de los romanos Nmeros enteros
Nmeros enteros Nmeros naturales
Nmeros naturales Yu chi ho
Yu chi ho Number line
Number line Nmeros ordinales
Nmeros ordinales Nmeros reales
Nmeros reales Nyuexternal
Nyuexternal Numeral cardinal ordinal
Numeral cardinal ordinal Nmeros ordinales
Nmeros ordinales Jose ruiz blasco
Jose ruiz blasco Florentino ulibarri
Florentino ulibarri Aportaciones de adolfo ruiz cortines
Aportaciones de adolfo ruiz cortines Eumenorreica
Eumenorreica Carolina ruiz wpi
Carolina ruiz wpi Ceip manuel ruiz zorrilla
Ceip manuel ruiz zorrilla La evaluación por competencias valora
La evaluación por competencias valora Ceip manuel ruiz zorrilla
Ceip manuel ruiz zorrilla Book de preguntas chilecompra 2020 con respuestas
Book de preguntas chilecompra 2020 con respuestas Fernanda valle desnuda
Fernanda valle desnuda