Rutgers University School of Engineering Spring 2015 14





![Concatenating Strings s = ['Albert', 'Einstein'] s = Albert. Einstein >> s = ['Albert', Concatenating Strings s = ['Albert', 'Einstein'] s = Albert. Einstein >> s = ['Albert',](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-7.jpg)

![Concatenating Vertically s = ['Apple'; 'IBM'; 'Microsoft']; ? ? ? Error using ==> vertcat Concatenating Vertically s = ['Apple'; 'IBM'; 'Microsoft']; ? ? ? Error using ==> vertcat](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-9.jpg)

![a = [143. 87, -0. 0000325, -7545]'; num 2 str >> s = num a = [143. 87, -0. 0000325, -7545]'; num 2 str >> s = num](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-11.jpg)
![a = [143. 87, -0. 0000325, -7545]'; >> s = num 2 str(a, '%10. a = [143. 87, -0. 0000325, -7545]'; >> s = num 2 str(a, '%10.](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-12.jpg)
![t = linspace(0, 5, 101); w = [2, 5, 8, 10]; Y = sin(w'*t); t = linspace(0, 5, 101); w = [2, 5, 8, 10]; Y = sin(w'*t);](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-13.jpg)






![s. a = [1 2; 3 4]; s. b = {'a', 'bb'; 'ccc', 'dddd'}; s. a = [1 2; 3 4]; s. b = {'a', 'bb'; 'ccc', 'dddd'};](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-22.jpg)


![A B C D = = {'Apple'; 'IBM'; 'Microsoft'}; [1 2; 3 4]; @(x) A B C D = = {'Apple'; 'IBM'; 'Microsoft'}; [1 2; 3 4]; @(x)](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-26.jpg)


![A B C D = = {'Apple'; 'IBM'; 'Microsoft'}; [1 2; 3 4]; @(x) A B C D = = {'Apple'; 'IBM'; 'Microsoft'}; [1 2; 3 4]; @(x)](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-29.jpg)




![>> d = c; >> % d(1, 3) = {[4 5 6]'}; >> d{1, >> d = c; >> % d(1, 3) = {[4 5 6]'}; >> d{1,](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-34.jpg)


![>> A = [1, 2; 3, 4]; % 2 x 2 matrix >> S >> A = [1, 2; 3, 4]; % 2 x 2 matrix >> S](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-38.jpg)

![M = {'January'; 'April'; 'July'; 'October'}; T 1 = [30; 60; 80; 70]; column M = {'January'; 'April'; 'July'; 'October'}; T 1 = [30; 60; 80; 70]; column](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-40.jpg)



![>> >> a = [1 2; 3 4]; A(: , 1) = a; A(: >> >> a = [1 2; 3 4]; A(: , 1) = a; A(:](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-44.jpg)





![>> a = [0, pi/6, pi/4, pi/2, pi]; >> cos(a) ans = 1 0. >> a = [0, pi/6, pi/4, pi/2, pi]; >> cos(a) ans = 1 0.](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-51.jpg)




![>> A = [sin(2*x), sin(3*x) cos(2*x), cos(3*x)] A = [ sin(2*x), sin(3*x)] [ cos(2*x), >> A = [sin(2*x), sin(3*x) cos(2*x), cos(3*x)] A = [ sin(2*x), sin(3*x)] [ cos(2*x),](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-56.jpg)


![numden >> [num, den] = numden(1 + 2*x + 3/(x^2+5)) num = 2*x^3 + numden >> [num, den] = numden(1 + 2*x + 3/(x^2+5)) num = 2*x^3 +](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-59.jpg)










![solving equations >> [x, y] = solve('x+y=1', 'x^2+y^2=1'); >> [x, y] ans = [ solving equations >> [x, y] = solve('x+y=1', 'x^2+y^2=1'); >> [x, y] ans = [](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-70.jpg)

![>> b = [12; -3; 11; 10]; >> x = inv(A)*b x = 1 >> b = [12; -3; 11; 10]; >> x = inv(A)*b x = 1](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-72.jpg)

![>> [q, mono] = coeffs(f) q = [ 5, -2, 1, 4, 3] mono >> [q, mono] = coeffs(f) q = [ 5, -2, 1, 4, 3] mono](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-74.jpg)










![v 0 = 0; va = 30; ta = 10; tspan = [0, 30]; v 0 = 0; va = 30; ta = 10; tspan = [0, 30];](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-86.jpg)

- Slides: 88

Rutgers University School of Engineering Spring 2015 14: 440: 127 - Introduction to Computers for Engineers Sophocles J. Orfanidis ECE Department orfanidi@ece. rutgers. edu week 13

Weekly Topics Week 1 - Basics – variables, arrays, matrices, plotting (ch. 2 & 3) Week 2 - Basics – operators, functions, strings, cells (ch. 2, 3, 11) Week 3 - Matrices (ch. 4) Week 4 - Plotting – 2 D and 3 D plots (ch. 5) Week 5 - User-defined functions (ch. 6) Week 6 - Input-output formatting – fprintf, fscanf (ch. 7) – Exam 1 Week 7 - Relational & logical operators, if, switch statements (ch. 8) Week 8 - For-loops, while-loops (ch. 9) Week 9 - Review for weeks 5 -8 Week 10 - Matrix algebra – solving linear equations (ch. 10) – Exam 2 Week 11 - Numerical methods I (ch. 13) Week 12 - Numerical methods II (ch. 13) Week 13 - Strings, structures, cell arrays, symbolic math (ch. 11, 12) Week 14 – Exam 3 References: H. Moore, MATLAB for Engineers, 4/e, Prentice Hall, 2014 G. Recktenwald, Numerical Methods with MATLAB, Prentice Hall, 2000 A. Gilat, MATLAB, An Introduction with Applications, 4/e, Wiley, 2011

Strings, Structures, Cells, Symbolic Math • • characters and strings concatenating strings using num 2 str comparing strings with strcmp • structure arrays • converting structures to cells • cell arrays • cell vs. content indexing • varargin, varargout • multi-dimensional arrays • symbolic math

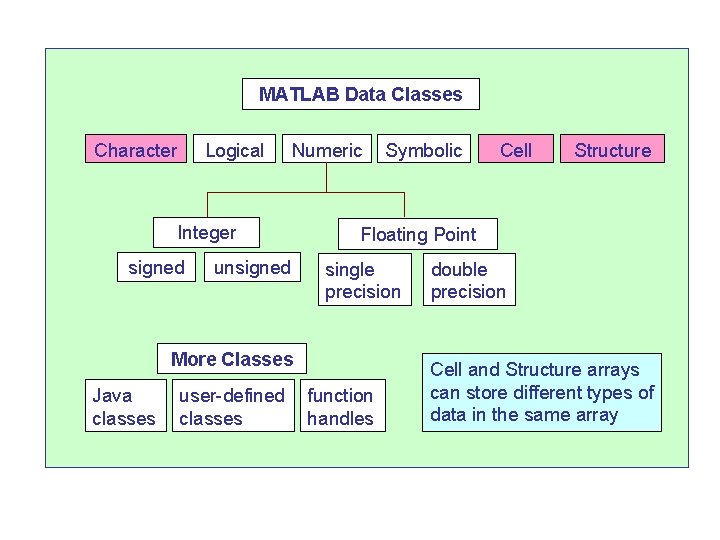
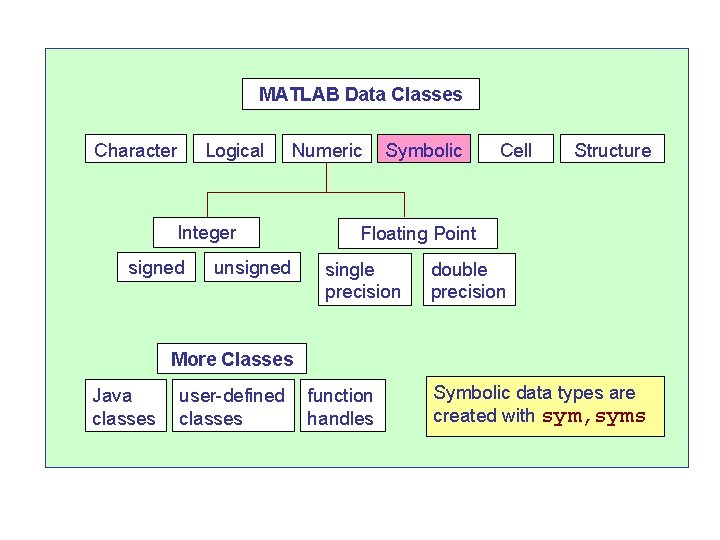
MATLAB Data Classes Character Logical Numeric Integer signed unsigned user-defined classes Cell Structure Floating Point single precision More Classes Java classes Symbolic function handles double precision Cell and Structure arrays can store different types of data in the same array

Characters and Strings >> c = 'A' c = A Strings are arrays of characters. Characters are represented internally by standardized numbers, referred to as ASCII (American Standard Code for Information Interchange) codes. see Wikipedia link: ASCII table >> x = double(c) x = 65 % ASCII code for 'A' >> char(x) ans = A >> class(c) ans = char() creates a character string >> doc char >> doc class

>> s = 'ABC DEFG' s = ABC DEFG >> x = double(s) x = 65 66 67 32 68 69 70 71 >> char(x) ans = ABC DEFG >> size(s) ans = 1 8 >> class(s) ans = char ASCII codes convert ASCII codes to characters s is a row vector of 8 characters >> s(2), s(3: 5) ans = B ans = C D
![Concatenating Strings s Albert Einstein s Albert Einstein s Albert Concatenating Strings s = ['Albert', 'Einstein'] s = Albert. Einstein >> s = ['Albert',](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-7.jpg)
Concatenating Strings s = ['Albert', 'Einstein'] s = Albert. Einstein >> s = ['Albert', ' Einstein'] s = Albert Einstein preserve leading and trailing spaces >> s = ['Albert ', 'Einstein'] s = >> doc Albert Einstein >> doc >> size(s) >> doc ans = >> doc 1 15 strcat strvcat num 2 str strcmp findstr

Concatenating Strings s = strcat('Albert ', 'Einstein') s = strcat strips trailing spaces Albert. Einstein but not leading spaces >> s = strcat('Albert', ' Einstein') s = Albert Einstein use repmat to make up long format strings for use with fprintf >> fmt = strcat(repmat('%8. 3 f ', 1, 6), 'n') fmt = %8. 3 fn
![Concatenating Vertically s Apple IBM Microsoft Error using vertcat Concatenating Vertically s = ['Apple'; 'IBM'; 'Microsoft']; ? ? ? Error using ==> vertcat](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-9.jpg)
Concatenating Vertically s = ['Apple'; 'IBM'; 'Microsoft']; ? ? ? Error using ==> vertcat CAT arguments dimensions are not consistent. s = ['Apple '; 'IBM s = Apple IBM Microsoft padded with spaces to the length of the longest string >> size(s) ans = 3 9 '; 'Microsoft']

Concatenating Vertically s = strvcat('Apple', 'IBM', 'Microsoft'); s = char('Apple', 'IBM', 'Microsoft'); s = Apple IBM Microsoft >> size(s) ans = 3 9 strvcat, char both pad spaces as necessary Recommendation: use char to concatenate vertically, and [] to concatenate horizontally
![a 143 87 0 0000325 7545 num 2 str s num a = [143. 87, -0. 0000325, -7545]'; num 2 str >> s = num](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-11.jpg)
a = [143. 87, -0. 0000325, -7545]'; num 2 str >> s = num 2 str(a) s = num 2 str(A) 143. 87 s = num 2 str(A, precision) -3. 25 e-005 s = num 2 str(A, format) -7545 >> s = num 2 str(a, 4) s = 143. 9 max number of digits -3. 25 e-005 -7545 >> s = num 2 str(a, '%12. 6 f') s = 143. 870000 format spec -0. 000032 -7545. 000000
![a 143 87 0 0000325 7545 s num 2 stra 10 a = [143. 87, -0. 0000325, -7545]'; >> s = num 2 str(a, '%10.](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-12.jpg)
a = [143. 87, -0. 0000325, -7545]'; >> s = num 2 str(a, '%10. 5 E') s = 1. 43870 E+002 -3. 25000 E-005 -7. 54500 E+003 b = char('A', 'BB', 'CCC'); >> disp([b, repmat(' A 1. 43870 E+002 BB -3. 25000 E-005 CCC -7. 54500 E+003 ', 3, 1), s]) num 2 str
![t linspace0 5 101 w 2 5 8 10 Y sinwt t = linspace(0, 5, 101); w = [2, 5, 8, 10]; Y = sin(w'*t);](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-13.jpg)
t = linspace(0, 5, 101); w = [2, 5, 8, 10]; Y = sin(w'*t); % 4 x 101 matrix s = char('b-', 'r-', 'm-', 'g-'); for i=1: 4, figure; plot(t, Y(i, : ), s(i, : )); title(['sin(', num 2 str(w(i)), 't)']); print('-depsc', ['file', num 2 str(i), '. eps']); end Labeling and saving multiple plots with num 2 str saved as file 1. eps, file 2. eps file 3. eps, file 4. eps

Comparing Strings are arrays of characters, so the condition s 1==s 2 requires both s 1 and s 2 to have the same length >> s 1 = 'short'; s 2 = 'shore'; >> s 1==s 1 ans = 1 1 1 >> s 1==s 2 ans = 1 1 0 >> s 1 = 'short'; s 2 = 'long'; >> s 1==s 2 ? ? ? Error using ==> eq Matrix dimensions must agree.

Comparing Strings Use strcmp to compare strings of unequal length, and get a binary decision >> s 1 = 'short'; s 2 = 'shore'; >> strcmp(s 1, s 1) ans = >> doc strcmp 1 >> doc strcmpi >> strcmp(s 1, s 2) ans = 0 >> s 1 = 'short'; s 2 = 'long'; >> strcmp(s 1, s 2) ans = 0 case-insensitive

Useful String Functions sprintf sscanf deblank strcmpi strmatch upper lower blanks strjust strtrim strrep findstr - write formatted string - read formatted string - remove trailing blanks - compare strings - find possible matches - convert to upper case - convert to lower case - string of blanks - left/right/center justify string - remove leading/trailing spaces - replace strings - find one string within another

Structures name. field Structures have named ‘fields’ that can store all kinds of data: vectors, matrices, strings, cell arrays, other structures student. name = 'Apple, A. '; student. id = 12345; student. exams = [85, 87, 90]; student. grades = {'B+', 'A'}; >> student = name: id: exams: grades: 'Apple, A. ' 12345 [85 87 90] {'B+' 'A'} % % string number vector cell >> class(student) ans = structures can also be created with struct()

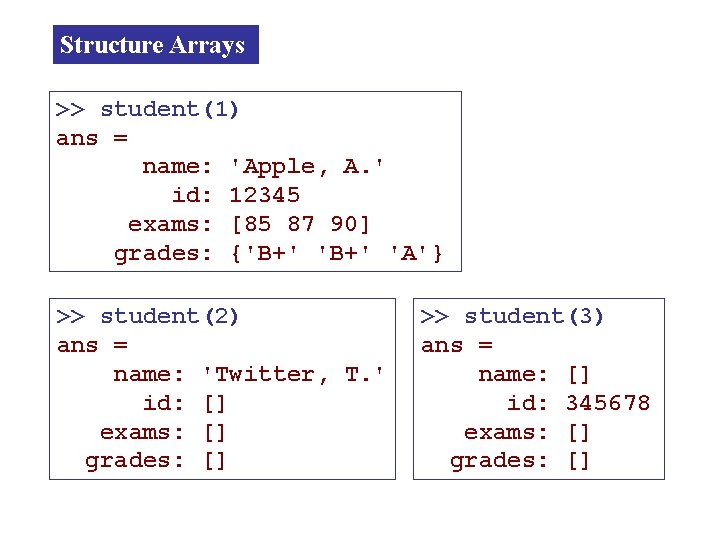
Structure Arrays structure array index add two more students with partially defined fields, rest of fields are still empty student(2). name = 'Twitter, T. '; student(3). id = 345678; >> student = 1 x 3 struct array with fields: name id exams grades

Structure Arrays >> student(1) ans = name: 'Apple, A. ' id: 12345 exams: [85 87 90] grades: {'B+' 'A'} >> student(2) ans = name: 'Twitter, T. ' id: [] exams: [] grades: [] >> student(3) ans = name: [] id: 345678 exams: [] grades: []

Structure Arrays the missing field values can be defined later and don’t have to be of the same type or length as those of the other entries >> student(3). exams = [70 80]; >> student(3) ans = name: [] id: 345678 exams: [70 80] grades: []

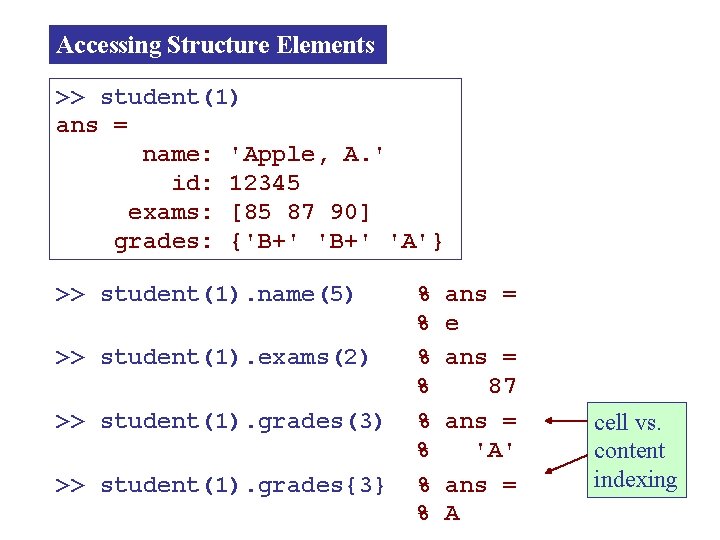
Accessing Structure Elements >> student(1) ans = name: 'Apple, A. ' id: 12345 exams: [85 87 90] grades: {'B+' 'A'} >> student(1). name(5) >> student(1). exams(2) >> student(1). grades(3) >> student(1). grades{3} % % % % ans = e ans = 87 ans = 'A' ans = A cell vs. content indexing
![s a 1 2 3 4 s b a bb ccc dddd s. a = [1 2; 3 4]; s. b = {'a', 'bb'; 'ccc', 'dddd'};](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-22.jpg)
s. a = [1 2; 3 4]; s. b = {'a', 'bb'; 'ccc', 'dddd'}; >> s s = a: [2 x 2 double] b: {2 x 2 cell} >> s. a ans = 1 3 >> s. a(2, 2) ans = 4 2 4 >> s. b ans = 'a' 'ccc' 'bb' 'dddd' >> s. b(2, 1), s. b{2, 1} ans = cell vs. 'ccc' content ans = indexing ccc

Nested Structures student. name = 'Apple, A. '; student. id = 12345; student. work. exams = [85, 87, 90]; student. work. grades = {'B+', 'A'}; >> student = name: 'Apple, A. ' id: 12345 work: [1 x 1 struct] >> student. work % sub-structure ans = exams: [85 87 90] grades: {'B+' 'A'}

Stucture Functions struct fieldnames isstruct isfield rmfield struct 2 cell - create structure get structure field names test if a structure test if a field remove a structure field convert structure to cell array >> C = struct 2 cell(student) C = 'Apple, A. ' [ 12345] [1 x 1 struct] >> C{3} content indexing ans = exams: [85 87 90] grades: {'B+' 'A'}

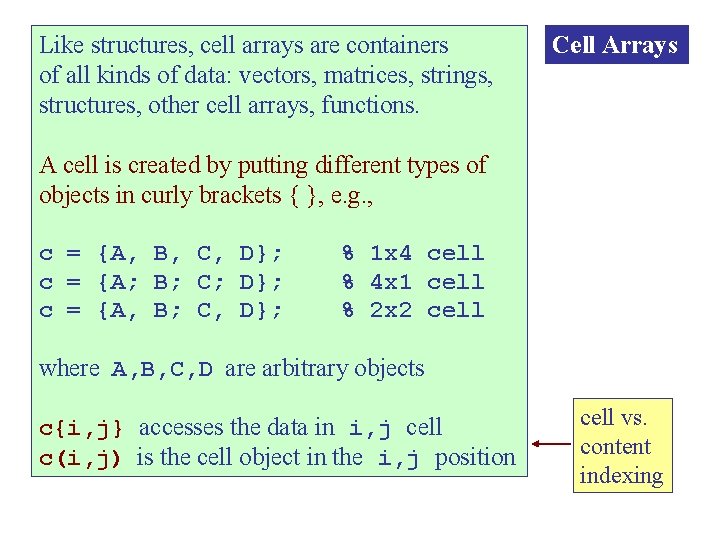
Like structures, cell arrays are containers of all kinds of data: vectors, matrices, strings, structures, other cell arrays, functions. Cell Arrays A cell is created by putting different types of objects in curly brackets { }, e. g. , c = {A, B, C, D}; c = {A; B; C; D}; c = {A, B; C, D}; % 1 x 4 cell % 4 x 1 cell % 2 x 2 cell where A, B, C, D are arbitrary objects c{i, j} accesses the data in i, j cell c(i, j) is the cell object in the i, j position cell vs. content indexing
![A B C D Apple IBM Microsoft 1 2 3 4 x A B C D = = {'Apple'; 'IBM'; 'Microsoft'}; [1 2; 3 4]; @(x)](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-26.jpg)
A B C D = = {'Apple'; 'IBM'; 'Microsoft'}; [1 2; 3 4]; @(x) x. ^2 + 1; [10 20 30 40 50]; c = {A, B; C, D} c = {3 x 1 cell} @(x)x. ^2+1 % % cells matrix function row % define 2 x 2 cell array [2 x 2 double] [1 x 5 double] >> cellplot(c);

A = {'Apple'; 'IBM'; 'Microsoft'} A = 'Apple' 'IBM' 'Microsoft' comparing cell arrays of strings vs. strings >> size(A), class(A) ans = 3 1 ans = cell S = char('Apple', 'IBM', 'Microsoft') S = Apple IBM Microsoft >> size(S), class(S) ans = 3 9 ans = char

>> A(2), class(A(2)) ans = 'IBM' ans = cell vs. content >> A{2}, class(A{2}) indexing ans = IBM ans = char >> A' ans = 'Apple' 'IBM' 'Microsoft' >> S Apple IBM Microsoft >> S' AIM p. Bi p. Mc l r e o s o f t
![A B C D Apple IBM Microsoft 1 2 3 4 x A B C D = = {'Apple'; 'IBM'; 'Microsoft'}; [1 2; 3 4]; @(x)](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-29.jpg)
A B C D = = {'Apple'; 'IBM'; 'Microsoft'}; [1 2; 3 4]; @(x) x. ^2 + 1; [10 20 30 40 50]; c = {A, B; C, D} c = {3 x 1 cell} @(x)x. ^2+1 % % cells matrix function row % define 2 x 2 cell array [2 x 2 double] [1 x 5 double] >> cellplot(c);

content indexing with { } >> celldisp(c) c{1, 1}{1} = Apple c{1, 1}{2} = IBM c{1, 1}{3} = Microsoft >> c{1, 1} ans = 'Apple' 'IBM' 'Microsoft' c{2, 1} = @(x)x. ^2+1 c{1, 2} = 1 3 2 4 c{2, 2} = 10 20 >> c{2, 1} ans = @(x)x. ^2+1 30 40 50

>> c{1, 1}{3} ans = Microsoft >> c{1, 1}{3}(6) ans = s content indexing with { } >> c{1, 2}(2, : ) ans = 3 4 >> x = [1 2 3]; >> c{2, 1}(x) ans = 2 5 10 >> c{1, 2}(1, 2) ans = 2 >> fplot(c{2, 1}, [0, 3]); >> c{2, 2}(3) ans = 30

cell indexing ( ) content indexing { } >> c(2, 2) cell ans = [1 x 5 double] >> class(c(2, 2)) ans = cell >> c{2, 2} ans = 10 20 cell contents 30 >> class(c{2, 2}) ans = double 40 50

>> c{1, 1}(2) ans = 'IBM' cell >> class(c{1, 1}(2)) ans = cell >> c{1, 1}{2} ans = IBM cell contents >> class(c{1, 1}{2}) ans = char cell indexing ( ) content indexing { }
![d c d1 3 4 5 6 d1 >> d = c; >> % d(1, 3) = {[4 5 6]'}; >> d{1,](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-34.jpg)
>> d = c; >> % d(1, 3) = {[4 5 6]'}; >> d{1, 3} = [4, 5, 6]' % define as cell % define content d = {3 x 1 cell} @(x)x. ^2+1 [3 x 1 double] [] [2 x 2 double] [1 x 5 double] >> d(2, 3) ans = {[]} >> d{2, 3} ans = [] >> cellplot(d);

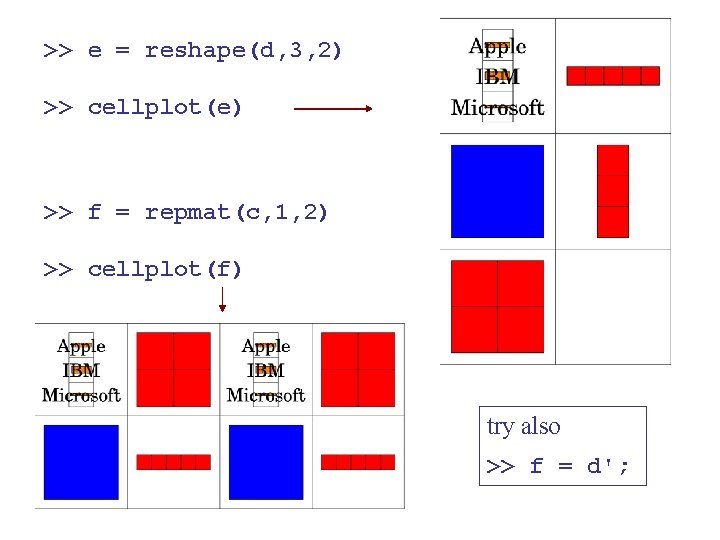
>> e = reshape(d, 3, 2) >> cellplot(e) >> f = repmat(c, 1, 2) >> cellplot(f) try also >> f = d';

>> c{1, 1}{2} = 'Google'; changing cell >> c{1, 2} = 10*c{1, 2}; array contents >> c{2, 2}(3) = 300; >> celldisp(c) c{1, 1}{1} = could have used: Apple c{1, 1}(2) = {'Google'}; c{1, 1}{2} = Google c{1, 1}{3} = why not ? Microsoft c(1, 2) = 10*c(1, 2); c{2, 1} = @(x)x. ^2+1 why not ? c{1, 2} = c{2, 2}{3} = 300; 10 20 30 40 c{2, 2} = 10 20 300 40 50

num 2 cell 2 mat converts numerical cell arrays to numbers num 2 cell converts numerical array to cell array >> A = [1 2; 3 4]; >> C = num 2 cell(A) C = [1] [3] [2] [4] >> B = cell 2 mat(C) B = 1 3 2 4
![A 1 2 3 4 2 x 2 matrix S >> A = [1, 2; 3, 4]; % 2 x 2 matrix >> S](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-38.jpg)
>> A = [1, 2; 3, 4]; % 2 x 2 matrix >> S = {'a', 'bb'; 'ccc', 'dddd'}; num 2 cell 2 mat % 2 x 2 cell S = 'a' 'ccc' 'bb' 'dddd' >> [A, S] % can’t mix numbers and cells ? ? ? Error using ==> horzcat CAT arguments dimensions are not consistent. >> [num 2 cell(A), S] ans = [1] [3] [2] [4] % construct 2 x 4 cell 'a' 'ccc' 'bb' 'dddd'

using num 2 cell with fprintf S = {'January', 'April', 'July', 'October'}; T = [30, 60, 80, 70]; C = ? ? ? CAT are [S; T] % can’t mix numbers and cells Error using ==> vertcat arguments dimensions not consistent. C = [S; num 2 cell(T)] % make all into cells C = 'January' [ 30] fprintf(' January April July October 'April' [ 60] %-7 s 30. 00 60. 00 80. 00 70. 00 'July' [ 80] 'October' [ 70] %5. 2 fn', C{: }); read content column-wise print it row-wise >> class(C) ans = cell >> C(: ) ans = 'January' [30] 'April' [60] 'July' [80] 'October' [70]
![M January April July October T 1 30 60 80 70 column M = {'January'; 'April'; 'July'; 'October'}; T 1 = [30; 60; 80; 70]; column](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-40.jpg)
M = {'January'; 'April'; 'July'; 'October'}; T 1 = [30; 60; 80; 70]; column vectors T 2 = [-10; 40; 60; 50]; transposed C = [M, num 2 cell([T 1, T 2])]' % C = % 'January' % [ 30] % [ -10] num 2 cell fprintf >> C(: ) 'April' [ 60] [ 40] 'July' [ 80] [ 60] 'October' [ 70] [ 50] fprintf(' T 1 T 2n') fprintf('-------------n') fprintf('%-7 s %6. 2 fn', C{: }) % fprintf('%-7 s %6. 2 fn', C{: , : }) T 1 T 2 ------------January 30. 00 -10. 00 April 60. 00 40. 00 July 80. 00 60. 00 October 70. 00 50. 00 content indexing ans = 'January' [ 30] [-10] 'April' [ 60] [ 40] 'July' [ 80] [ 60] 'October' [ 70] [ 50]

varargin varargout varargin, varargout are cell arrays that allow the passing a variable number of function inputs & outputs % [x, y, vx, vy] = trajectory(t, v 0, th 0, g) function [varargout] = trajectory(t, v 0, varargin) Nin = nargin-2; % number of varargin inputs if Nin==0, th 0=90; h 0=0; g=9. 81; end if Nin==1, th 0=varargin{1}; h 0=0; g=9. 81; end if Nin==2, th 0=varargin{1}; . . . h 0=varargin{2}; g=9. 81; end if Nin==3, th 0=varargin{1}; . . . h 0=varargin{2}; g=varargin{3}; end continues

th 0 = th 0 * pi/180; % convert to radians x = v 0 * cos(th 0) * t; y = h 0 + v 0 * sin(th 0) * t - 1/2 * g * t. ^2; vx = v 0 * cos(th 0); vy = v 0 * sin(th 0) - g * t; if nargout==1; varargout{1} if nargout==2; varargout{1} varargout{2} if nargout==3; varargout{1} varargout{2} varargout{3} if nargout==4; varargout{1} varargout{2} varargout{3} varargout{4} = = = = = x; end x; . . . y; end x; y; . . . vx; end x; . . . y; . . . vx; . . . vy; end

Multidimensional Arrays A three-dimensional array is a collection of two-dimensional matrices of the same size, and are characterized by triple indexing, e. g. , A(i, j, p) is the (i, j) matrix element of the p-th matrix. Higher-dimensional arrays can also be defined, e. g. , a 4 D array is a collection of 3 D arrays of the same size. applications in video processing
![a 1 2 3 4 A 1 a A >> >> a = [1 2; 3 4]; A(: , 1) = a; A(:](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-44.jpg)
>> >> a = [1 2; 3 4]; A(: , 1) = a; A(: , 2) = 10*a; A(: , 3) = 100*a; >> A A(: , 1) = 1 2 3 4 A(: , 2) = 10 20 30 40 A(: , 3) = 100 200 300 400 pages sum, min, max can operate along the i, j, p dimensions

A(: , 1) = 1 2 3 4 A(: , 2) = 10 20 30 40 A(: , 3) = 100 200 300 400 >> sum(A, 3) ans = 111 222 333 444 >> sum(A, 1) ans(: , 1) = 4 6 ans(: , 2) = 40 60 ans(: , 3) = 400 600 >> sum(A, 2) ans(: , 1) = 3 7 ans(: , 2) = 30 70 ans(: , 3) = 300 700

A(: , 1) = 1 2 3 4 A(: , 2) = 10 20 30 40 A(: , 3) = 100 200 300 400 >> min(A, [], 3) ans = 1 2 3 4 >> min(A, [], 1) ans(: , 1) = 1 2 ans(: , 2) = 10 20 ans(: , 3) = 100 200 >> min(A, [], 2) ans(: , 1) = 1 3 ans(: , 2) = 10 30 ans(: , 3) = 100 300

A(: , 1) = 1 2 3 4 A(: , 2) = 10 20 30 40 A(: , 3) = 100 200 300 400 column-order across pages >> A>20 & A<300 ans(: , 1) = 0 0 ans(: , 2) = 0 0 1 1 ans(: , 3) = 1 1 0 0 >> k = find(A>20 & A<300) k = 6 8 9 11

Symbolic Math Toolbox • • • Creating and manipulating symbolic variables Factoring and simplifying algebraic expressions Solving symbolic equations Linear algebra operations Performing summation of infinite series Taylor series expansions, limits Differentiation and integration Solving differential equations Fourier, Laplace, Z-transforms and inverses Variable precision arithmetic

MATLAB Data Classes Character Logical Numeric Integer signed unsigned Symbolic Cell Structure Floating Point single precision double precision More Classes Java classes user-defined classes function handles Symbolic data types are created with sym, syms

>> syms x y z real >> syms x y z positive >> x = sym('x'); >> f = x^6 -1 f = x^6 - 1 >> g = x^3 +1 g = x^3 + 1 >> >> help symbolic doc syms >> sym(sqrt(2)) ans = 2^(1/2) >> sqrt(sym(2)) ans = 2^(1/2) >> double(ans) ans = 1. 4142
![a 0 pi6 pi4 pi2 pi cosa ans 1 0 >> a = [0, pi/6, pi/4, pi/2, pi]; >> cos(a) ans = 1 0.](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-51.jpg)
>> a = [0, pi/6, pi/4, pi/2, pi]; >> cos(a) ans = 1 0. 8660 0. 7071 >> c = cos(sym(a)) c = [ 1, 3^(1/2)/2, 2^(1/2)/2, >> symdisp(c) display symbolic expression using La. Te. X – on sakai 0 -1 0, -1] >> pretty(c) +-+ | 1/2 | | 3 2 | | 1, ----, 0, -1 | | 2 2 | +-+

>> f = x^6 -1; >> g = x^3 +1; >> r = f/g % x^6 -1 = (x^3 -1)*(x^3+1) r = (x^6 - 1)/(x^3 + 1) >> pretty(r) 6 x - 1 ------3 x + 1 >> symdisp(r) % pretty print

Functions for factoring and simplification of algebraic expressions: simplify expand factor collect simple numden subs - Simplify Expand Factor Collect Search for shortest form Numerator and denominator Symbolic substitution

factor >> simplify(r) ans = x^3 - 1 >> factor(simplify(r)) ans = (x - 1)*(x^2 + x + 1) % x^3 - 1 >> factor(g) ans = (x + 1)*(x^2 - x + 1) % x^3 + 1 >> factor(f) % x^6 - 1 ans = (x - 1)*(x + 1)*(x^2 + x + 1)*(x^2 - x + 1)

>> syms x a b; >> expand((x+1)*(x+2)) ans = x^2 + 3*x + 2 >> expand(exp(a+b)) ans = exp(a)*exp(b) >> expand(cos(a+b)) ans = cos(a)*cos(b) - sin(a)*sin(b) >> expand(cosh(a+b)) ans = sinh(a)*sinh(b) + cosh(a)*cosh(b) expand
![A sin2x sin3x cos2x cos3x A sin2x sin3x cos2x >> A = [sin(2*x), sin(3*x) cos(2*x), cos(3*x)] A = [ sin(2*x), sin(3*x)] [ cos(2*x),](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-56.jpg)
>> A = [sin(2*x), sin(3*x) cos(2*x), cos(3*x)] A = [ sin(2*x), sin(3*x)] [ cos(2*x), cos(3*x)] expand >> B = expand(A) B = [2*cos(x)*sin(x), 3*cos(x)^2*sin(x)-sin(x)^3] [cos(x)^2 -sin(x)^2, cos(x)^3 -3*cos(x)*sin(x)^2] >> expand((a+b)*(a^2+2*a*b+b^2)) ans = a^3 + 3*a^2*b + 3*a*b^2 + b^3

>> collect((x+1)*(x+2)) ans = x^2 + 3*x + 2 collect >> collect((a+b)*(a^2 + 2*a*b + b^2), a) ans = a^3 + (3*b)*a^2 + (3*b^2)*a + b^3 >> collect((a+b)*(a^2 + 2*a*b + b^2), b) ans = b^3 + (3*a)*b^2 + (3*a^2)*b + a^3 >> factor(a^3 + 3*a^2*b + 3*a*b^2 + b^3) ans = (a + b)^3

simplify >> simplify(a^3 + 3*a^2*b + 3*a*b^2 + b^3) ans = (a + b)^3 >> simplify(cos(b)*sin(a) - cos(a)*sin(b)) ans = sin(a - b) B = [2*cos(x)*sin(x), 3*cos(x)^2*sin(x)-sin(x)^3] [cos(x)^2 -sin(x)^2, cos(x)^3 -3*cos(x)*sin(x)^2] >> simplify(B) ans = [ sin(2*x), sin(3*x)] [ cos(2*x), cos(3*x)]
![numden num den numden1 2x 3x25 num 2x3 numden >> [num, den] = numden(1 + 2*x + 3/(x^2+5)) num = 2*x^3 +](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-59.jpg)
numden >> [num, den] = numden(1 + 2*x + 3/(x^2+5)) num = 2*x^3 + x^2 + 10*x + 8 den = x^2 + 5 >> symdisp(1 + 2*x + 3/(x^2+5)) >> symdisp(num/den)

>> syms x a b >> y = a*x+b y = b + a*x x, a, b class sym subs >> y 1 = subs(y, a, 3) y 1 = b + 3*x >> y 2 = subs(y, b, 5) y 2 = a*x + 5 >> y 3 = subs(y, {a, b}, {3, 5}) y 3 = a, b taken from workspace 3*x + 5 >> a=2; b=4; y 4 = subs(y) y 4 = a, b class double 2*x + 4

Functions for solving algebraic and differential equations: solve dsolve finverse compose - solve algebraic equations. solve differential equations. Functional inverse. Functional composition.

Solving symbolic equations >> syms x a b c; >> f = a*x^2 + b*x + c; >> xsol = solve(f) xsol = -(b + (b^2 - 4*a*c)^(1/2))/(2*a) -(b - (b^2 - 4*a*c)^(1/2))/(2*a) >> xsol(1), xsol(2) ans = -(b + (b^2 - 4*a*c)^(1/2))/(2*a) ans = -(b - (b^2 - 4*a*c)^(1/2))/(2*a) symdisp(xsol(1));

>> g = a*(x-xsol(1))*(x-xsol(2)) g = a*(x + (b^2 - 4*a*c)^(1/2))/(2*a))*(x + (b - (b^2 - 4*a*c)^(1/2))/(2*a)) >> simplify(g) ans = a*x^2 + b*x + c >> a*xsol(1)^2 + b*xsol(1) + c ans = c + (b^2 - 4*a*c)^(1/2))^2/(4*a) (b*(b + (b^2 - 4*a*c)^(1/2)))/(2*a) >> simplify(a*xsol(1)^2 + b*xsol(1) + c) ans = 0

some variations >> >> xsol = = solving equations solve('a*x^2 + b*x + c'); solve('a*x^2 + b*x + c=0'); solve('a*x^2 + b*x + c', 'x'); solve(a*x^2 + b*x + c, x); >> syms z; >> xsol = solve(a*z^2 + b*z + c) xsol = -(b + (b^2 - 4*a*c)^(1/2))/(2*a) -(b - (b^2 - 4*a*c)^(1/2))/(2*a) >> bsol = solve(a*x^2 + b*x + c, b) bsol = -(a*x^2 + c)/x

>> syms a b p u w y z >> solve(a+b+p), solve(a+b+w) ans = - a - b how does it know >> solve(u+w+z) which variable ans = to solve for? - u - z alphabetically >> solve(w+y+z) closest to ‘x’ ans = - w - z >> syms x a b c; >> f = a*x^2 + b*x + c; >> xsol = solve(f) xsol = -(b + (b^2 - 4*a*c)^(1/2))/(2*a) -(b - (b^2 - 4*a*c)^(1/2))/(2*a) solving equations

>> f 1 = subs(f, {a, b, c}, {1, 1, -1}) f 1 = x^2 + x – 1 solving equations >> x 1 = solve(f 1) x 1 = 5^(1/2)/2 - 1/2 - 5^(1/2)/2 – 1/2 x 1 class sym >> subs(xsol, {a, b, c}, {1, 1, -1}) ans = -1. 6180 class double 0. 6180 >> phi = simplify(1. /x 1) phi = golden ratio 5^(1/2)/2 + 1/2 - 5^(1/2)/2

Fibonacci numbers, F(n) = F(n-1)+F(n-2) = [0, 1, 1, 2, 3, 5, 8, 13, …] >> syms n >> F = (phi(1)^n – phi(2)^n)/(phi(1)-phi(2)); >> simplify(F - subs(F, n, n-1) - subs(F, n, n-2)) ans = 0 >> limit(F/subs(F, n, n-1), n, inf) ans = 2/(5^(1/2) - 1) >> simplify(limit(F/subs(F, n, n-1), n, inf)) ans = 5^(1/2)/2 + 1/2 golden ratio

solving equations >> eq 1 = 'x^2 + x -1=0'; >> solve(eq 1) ans = 5^(1/2)/2 - 1/2 - 5^(1/2)/2 - 1/2 >> eq 2 = '1/x = x/(1 -x)'; >> solve(eq 2) ans = 5^(1/2)/2 - 1/2 - 5^(1/2)/2 - 1/2 >> solve('1/x = x/(1 -x)');

solving equations >> eq 1 = 'x^2 + y - 1=0'; >> eq 2 = 'x+y=0'; >> [x, y] = solve(eq 1, eq 2) x = 5^(1/2)/2 + 1/2 - 5^(1/2)/2 y = - 5^(1/2)/2 - 1/2 5^(1/2)/2 – 1/2 >> eval(x) ans = 1. 6180 -0. 6180 % or, double(x)
![solving equations x y solvexy1 x2y21 x y ans solving equations >> [x, y] = solve('x+y=1', 'x^2+y^2=1'); >> [x, y] ans = [](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-70.jpg)
solving equations >> [x, y] = solve('x+y=1', 'x^2+y^2=1'); >> [x, y] ans = [ 1, 0] [ 0, 1] >> S = solve('x+y=1', 'x^2+y^2=1') S = x: [2 x 1 sym] returned as a y: [2 x 1 sym] structure of syms >> [S. x, S. y] ans = [ 1, 0] [ 0, 1]

>> A = [ 5 1 3 0 1 4 1 1 -1 2 6 -2 1 -1 1 4]; >> A = sym(A) A = [ 5, 1, 3, 0] [ 1, 4, 1, 1] [ -1, 2, 6, -2] [ 1, -1, 1, 4] >> inv(A) ans = [ 53/274, [ -21/548, [ 13/548, [ -35/548, linear equations from homework-9 -2/137, -11/274] 34/137, -3/274, -37/548] -8/137, 41/274, 49/548] 11/137, -5/274, 121/548]
![b 12 3 11 10 x invAb x 1 >> b = [12; -3; 11; 10]; >> x = inv(A)*b x = 1](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-72.jpg)
>> b = [12; -3; 11; 10]; >> x = inv(A)*b x = 1 -2 3 1 >> class(x) ans = sym % or, Ab linear equations

>> f = 5*x^4 - 2*x^3 + x^2 + 4*x + 3 polynomials >> p = sym 2 poly(f) p = 5 -2 1 4 >> poly 2 sym(p) ans = 5*x^4 - 2*x^3 + x^2 + 4*x + 3 3 >> poly 2 sym(p, 't') ans = 5*t^4 - 2*t^3 + t^2 + 4*t + 3 poly 2 sym 2 poly coeffs quorem roots poly
![q mono coeffsf q 5 2 1 4 3 mono >> [q, mono] = coeffs(f) q = [ 5, -2, 1, 4, 3] mono](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-74.jpg)
>> [q, mono] = coeffs(f) q = [ 5, -2, 1, 4, 3] mono = [ x^4, x^3, x^2, x, 1] >> p = sym 2 poly(f) p = 5 -2 1 >> z = roots(p) z = 0. 7393 + 0. 8967 i 0. 7393 - 0. 8967 i -0. 5393 + 0. 3916 i -0. 5393 - 0. 3916 i polynomials 4 3 poly 2 sym 2 poly coeffs quorem roots poly

>> p = sym 2 poly(f) p = 5 -2 1 4 3 polynomials >> z = roots(p) z = 0. 7393 + 0. 8967 i 0. 7393 - 0. 8967 i -0. 5393 + 0. 3916 i -0. 5393 - 0. 3916 i >> P = poly(z) P = 1. 0 -0. 4 >> 5*P ans = 5 -2 poly 2 sym 2 poly coeffs quorem roots poly 0. 2 1 0. 8 4 0. 6 3

>> f = 5*x^4 - 2*x^3 + x^2 + 4*x + 3; >> x 1 = linspace(-1, 1, 201); >> f 1 = subs(f, x 1); >> plot(x 1, f 1, 'b'); >> xlabel('x'); >> ylabel('f(x)'); % or, f 1 = subs(f, x, x 1);

symsum >> syms n >> symsum(1/n^2, n, 1, inf) ans = pi^2/6 >> symsum(1/n^4, n, 1, inf) ans = pi^4/90

>> syms x n N symsum >> symsum(x^n, n, 0, N-1) piecewise([x = 1, N], [x <> 1, . . . (x^N - 1)/(x - 1)]) finite & infinite geometric series >> symsum(x^n, n, 0, inf) piecewise([1 <= x, Inf], . . . [abs(x) < 1, -1/(x - 1)]) >> symsum(x^n/sym('n!'), n, 0, inf) ans = exp(x) >> symsum(n^2, n, 1, N) ans = (N*(2*N + 1)*(N + 1))/6

>> syms x Taylor series >> taylor(exp(x)) ans = x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1 >> taylor(exp(x), 4) ans = x^3/6 + x^2/2 + x + 1 >> taylor(sin(x), 4) ans = x - x^3/6 >> taylor(sin(x)/x) ans = x^4/120 - x^2/6 + 1

>> syms x limits >> limit(exp(-x), x, inf) ans = 0 >> limit(sin(x)/x, x, 0) ans = 1 >> limit(cos(pi*cos(x)/2)/x, x, 0) ans = 0 >> taylor(cos(pi*cos(x)/2)/x, 2) ans = (pi*x)/4

>> syms x simple calculus >> diff(x^2) ans = 2*x >> int(x^2) ans = x^3/3 differentiation integration >> diff(x^3) ans = 3*x^2 >> int(cos(x)) ans = sin(x) >> diff(cos(x)) ans -sin(x) >> int(cos(x)^2, 0, pi) ans = pi/2

acceleration with air drag dsolve terminal velocity and time constant solve with initial velocity v(0) = v 0 exact solution

>> syms v t va ta v 0 D = derivative dsolve >> diffeq = 'Dv=va/ta*(1 -v^2/va^2)'; >> v = dsolve(diffeq, 'v(0)=v 0') v = -va*tan(-va*(- t/(ta*va) + (atan((v 0*i)/va)*i)*i >> v = simplify(v) v = va^2/v 0 + (va*(v 0^2 - va^2))/(v 0*(va + v 0*tanh(t/ta))) >> [num, den] = numden(v);

dsolve >> v = num/den v = (tanh(t/ta)*va^2 + v 0*va)/(va + v 0*tanh(t/ta)) >> symdisp(v); >> u = va*tanh(t/ta + atanh(v 0/va)); >> simplify(v-u) ans = 0

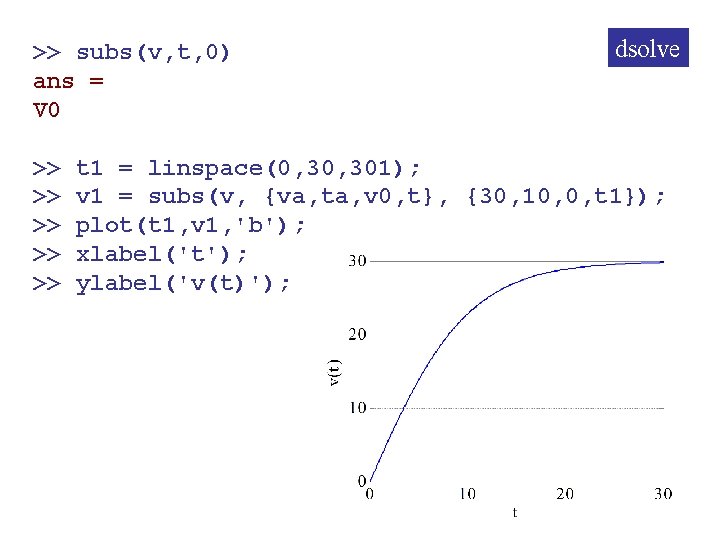
>> subs(v, t, 0) ans = V 0 >> >> >> dsolve t 1 = linspace(0, 301); v 1 = subs(v, {va, ta, v 0, t}, {30, 10, 0, t 1}); plot(t 1, v 1, 'b'); xlabel('t'); ylabel('v(t)');
![v 0 0 va 30 ta 10 tspan 0 30 v 0 = 0; va = 30; ta = 10; tspan = [0, 30];](https://slidetodoc.com/presentation_image/d3d7fc57f820e26c404e9a0b234fcb1d/image-86.jpg)
v 0 = 0; va = 30; ta = 10; tspan = [0, 30]; vdot = @(t, v) va/ta * (1 - v. ^2/va^2); [t 2, v 2] = ode 45(vdot, tspan, v 0); plot(t 2, v 2, 'r-') xlabel('t'); ylabel('v(t)'); compare exact and numerical solutions using ode 45 dsolve

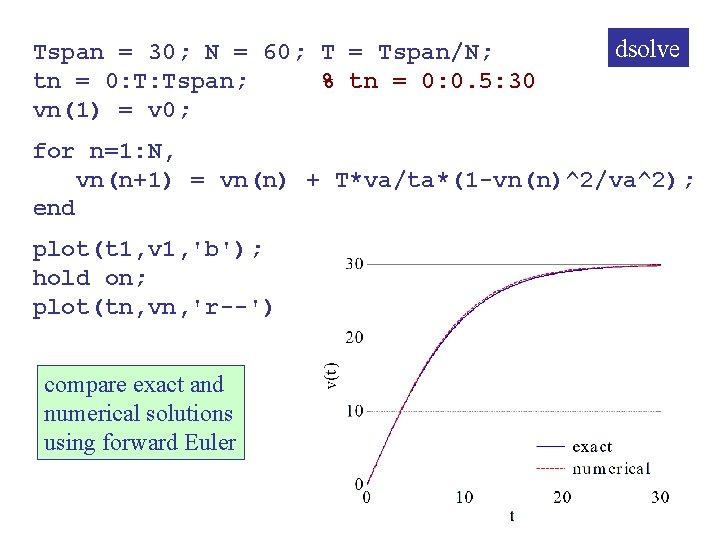
compare exact and numerical solutions using forward Euler method, which replaces derivatives by forward differences dsolve

Tspan = 30; N = 60; T = Tspan/N; tn = 0: T: Tspan; % tn = 0: 0. 5: 30 vn(1) = v 0; dsolve for n=1: N, vn(n+1) = vn(n) + T*va/ta*(1 -vn(n)^2/va^2); end plot(t 1, v 1, 'b'); hold on; plot(tn, vn, 'r--') compare exact and numerical solutions using forward Euler
 Spring break 2015
Spring break 2015 Spring summer fall winter and spring cast
Spring summer fall winter and spring cast Winter spring autumn summer
Winter spring autumn summer Rutgers dental interview
Rutgers dental interview Aalto university school of engineering
Aalto university school of engineering University of belgrade school of electrical engineering
University of belgrade school of electrical engineering Glennan building cwru
Glennan building cwru Graduate school of engineering science osaka university
Graduate school of engineering science osaka university Thomas j watson school of engineering
Thomas j watson school of engineering Oxford university press answer
Oxford university press answer Http://space-facts.com/the-moon/
Http://space-facts.com/the-moon/ Big spring school district
Big spring school district North spring primary school
North spring primary school West spring secondary school
West spring secondary school Big spring school district
Big spring school district Capri spring school
Capri spring school Coral springs middle school attendance line
Coral springs middle school attendance line Rutgers center for cognitive science
Rutgers center for cognitive science Webreh
Webreh Rutgers law symplicity
Rutgers law symplicity Marian
Marian Rutgers pharmaceutical industry fellowship
Rutgers pharmaceutical industry fellowship Rutgers gsbs
Rutgers gsbs Sona systems uci
Sona systems uci Rutgers library database
Rutgers library database Eden.rutgers.edu
Eden.rutgers.edu Bill welsh rutgers
Bill welsh rutgers Michael bordo rutgers
Michael bordo rutgers Computer science department rutgers
Computer science department rutgers Imielinski rutgers
Imielinski rutgers Rutgers cs 314
Rutgers cs 314 Rutgers cait
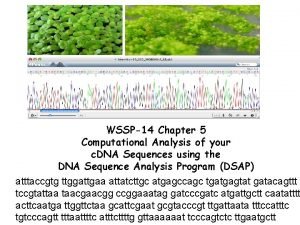
Rutgers cait Wssp rutgers
Wssp rutgers Dsap rutgers
Dsap rutgers Rutgers ocean temperatures
Rutgers ocean temperatures Rutgers ecrt
Rutgers ecrt Rutgers enrollment pathway
Rutgers enrollment pathway Joe markert
Joe markert Krzyzanowski rutgers
Krzyzanowski rutgers Data mining for business intelligence rutgers
Data mining for business intelligence rutgers Micromedex rutgers
Micromedex rutgers Rutgers ethernet
Rutgers ethernet Hksa240
Hksa240 Tina pappas
Tina pappas Rutgers micromedex
Rutgers micromedex Nbdn rutgers
Nbdn rutgers Bill welsh rutgers
Bill welsh rutgers Jolien rutgers
Jolien rutgers Tefko saracevic
Tefko saracevic Sas core classes
Sas core classes Scott glenn rutgers
Scott glenn rutgers Matthew stone rutgers
Matthew stone rutgers Vodacom zimbra email login
Vodacom zimbra email login Rutgers handshake
Rutgers handshake Boggs center rutgers
Boggs center rutgers Linata rutgers
Linata rutgers Rutgers osha verification
Rutgers osha verification Ivan marsic rutgers
Ivan marsic rutgers Njsams rutgers
Njsams rutgers Zimbra sfu
Zimbra sfu System architecture example
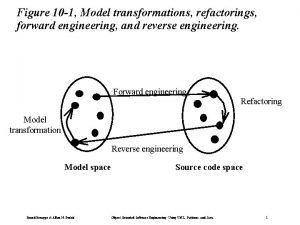
System architecture example Forward engineering in software engineering
Forward engineering in software engineering Engineering elegant systems: theory of systems engineering
Engineering elegant systems: theory of systems engineering Engineering elegant systems: theory of systems engineering
Engineering elegant systems: theory of systems engineering Forward and reverse engineering
Forward and reverse engineering Yildiz technical university mechanical engineering
Yildiz technical university mechanical engineering University of bridgeport computer science faculty
University of bridgeport computer science faculty Tel aviv university electrical engineering
Tel aviv university electrical engineering Louisiana tech university engineering
Louisiana tech university engineering Oakland university engineering center
Oakland university engineering center Temple university environmental engineering
Temple university environmental engineering Chemical engineering wisconsin
Chemical engineering wisconsin University of twente biomedical engineering
University of twente biomedical engineering Utah state university engineering
Utah state university engineering University of bridgeport computer science
University of bridgeport computer science Gwu electrical engineering
Gwu electrical engineering Sjsu mechanical engineering
Sjsu mechanical engineering Engineering statistics philadelphia university
Engineering statistics philadelphia university King saud university mechanical engineering
King saud university mechanical engineering Feup university of porto
Feup university of porto Air university software engineering
Air university software engineering Czech technical university mechanical engineering
Czech technical university mechanical engineering Clemson university electrical engineering
Clemson university electrical engineering University of wisconsin-madison biomedical engineering
University of wisconsin-madison biomedical engineering American university mechanical engineering
American university mechanical engineering American university mechanical engineering
American university mechanical engineering Electrical engineering northwestern
Electrical engineering northwestern Yale university mechanical engineering
Yale university mechanical engineering Faculty of civil engineering ctu prague
Faculty of civil engineering ctu prague