Quantum Communication Complexity Richard Cleve Institute for Quantum

Quantum Communication Complexity Richard Cleve Institute for Quantum Computing University of Waterloo Aug 2, 2005 1

1. Preliminaries 2

How does quantum information affect the communication costs of information processing tasks? • Potential applications • Context in which to explore interesting properties of quantum information • Interplay with quantum algorithms, nonlocality, and information theory 3

How much classical information in n qubits? 2 n 1 complex numbers are needed to describe an arbitrary n-qubit pure quantum state: 000 + 001 + 010 + + 111 Does this mean that an exponential amount of classical information is somehow stored in n qubits? No … Holevo’s Theorem [1973] implies: cannot extract more than n bits from n qubits 4

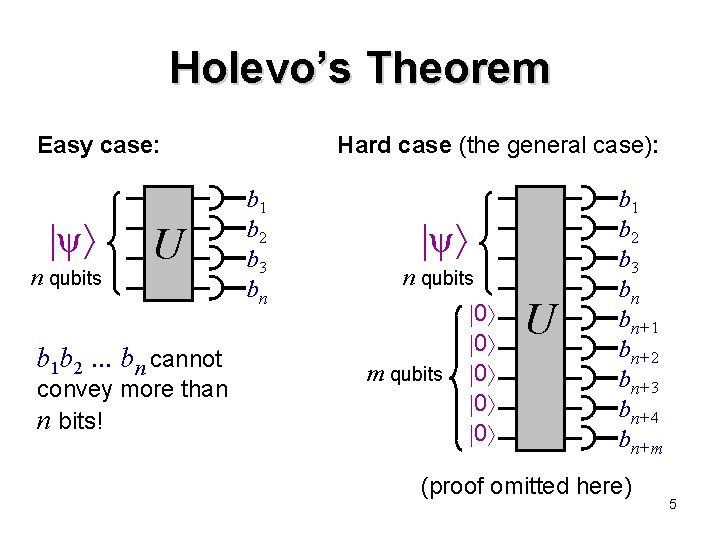
Holevo’s Theorem Easy case: ψ n qubits U b 1 b 2. . . bn cannot convey more than n bits! Hard case (the general case): b 1 b 2 b 3 bn ψ n qubits m qubits 0 0 0 U b 1 b 2 b 3 bn bn+1 bn+2 bn+3 bn+4 bn+m (proof omitted here) 5

Entanglement & signaling Example of an entangled state: qubit Can be used to perform some intriguing feats, such as teleportation, superdense coding, and “pseudo-telepathy” Can entangled states be used to “signal instantaneously”? No … any operation performed on one qubit has no affect on the state of the other qubit 6

Basic communication scenario Goal: convey n bits from Alice to Bob x 1 x 2 xn Alice Resources Bob x 1 x 2 xn 7

Basic communication scenario Bit communication: Cost: n Bit communication & prior entanglement: Cost: n [H ’ 73] [BW ’ 92] Qubit communication: Cost: n Qubit communication & prior entanglement: Cost: n/2 superdense coding 8

2. Communication complexity 9

Classical communication complexity x 1 x 2 xn y 1 y 2 yn f (x, y) E. g. equality function: f (x, y) = 1 if x = y, and 0 if x y Any deterministic protocol requires n bits communication Probabilistic protocols can solve with only O(log(n/ )) bits communication (error probability ) [Yao ’ 79] 10

Classical communication complexity x 1 x 2 xn y 1 y 2 yn x = y? Probabilistic protocol for Equality ( = 1/n): px(T) = x 0 + x 1 T + x 2 T 2 + … + xn 1 T n 1 py(T) = y 0 + y 1 T + y 2 T 2 + … + yn 1 T n 1 Arithmetic modulo m, for a prime m between n 2 and 2 n 2 Alice: pick random t {0, 1, …, m 1} send (t, px(t ) mod m) to Bob (this is only 4 log (n) bits) Bob: accept iff px(t) = py(t) mod m (err prob < n/n 2 = 1/n) 11

Quantum communication complexity x 1 x 2 xn y 1 y 2 yn Qubit communication qubits Prior entanglement entangled qubits x 1 x 2 xn y 1 y 2 yn bits [Y ’ 93] [CB ’ 97] f (x, y) 12

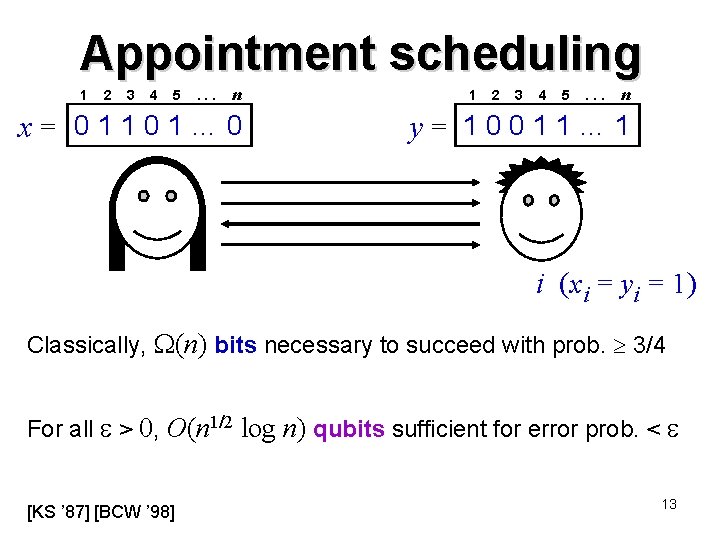
Appointment scheduling 1 2 3 4 5 . . . n x= 01101… 0 1 2 3 4 5 . . . n y= 10011… 1 i (xi = yi = 1) Classically, (n) bits necessary to succeed with prob. 3/4 For all > 0, O(n 1/2 log n) qubits sufficient for error prob. < [KS ’ 87] [BCW ’ 98] 13

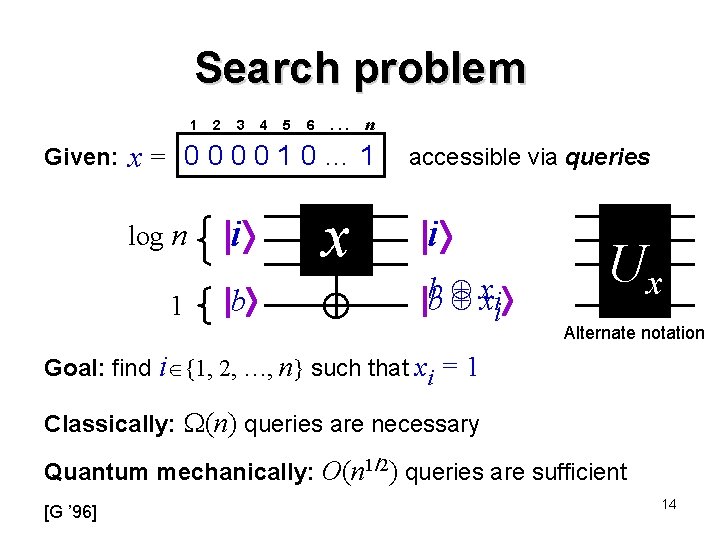
Search problem 1 Given: 2 3 4 5 6 . . . n x= 000010… 1 log n i 1 b b x accessible via queries i b b xxii Ux Alternate notation Goal: find i {1, 2, …, n} such that xi = 1 Classically: (n) queries are necessary Quantum mechanically: O(n 1/2) queries are sufficient [G ’ 96] 14

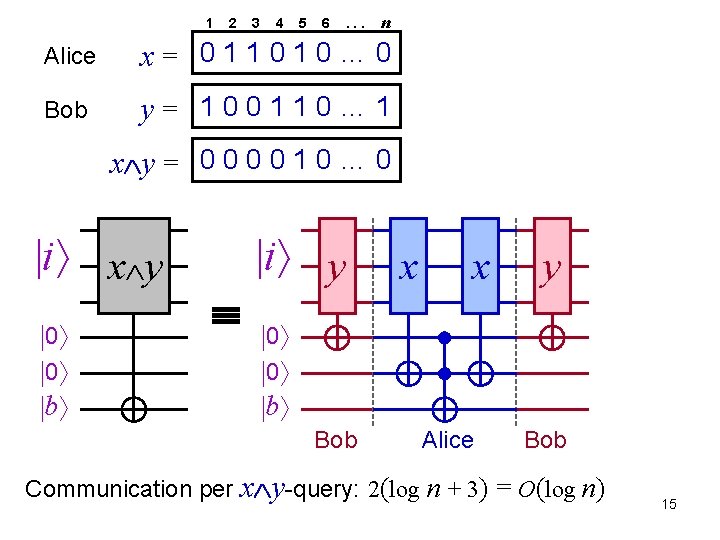
1 2 3 4 5 6 . . . n Alice x= 011010… 0 Bob y= 100110… 1 x y = 0 0 1 0 … 0 i x y 0 0 b i y x x y 0 0 b Bob Alice Bob Communication per x y-query: 2(log n + 3) = O(log n) 15

Appointment scheduling: epilogue Bit communication: Cost: θ( n) Bit communication & prior entanglement: Cost: θ( n 1/2) [R ’ 02] [AA ’ 03] Qubit communication: nn 1/21/2)log(n)) Cost: θ( O( Qubit communication & prior entanglement: Cost: θ( n 1/2) 16

Restricted version of equality Precondition (i. e. promise): either x = y or (x, y) = n/2 Hamming distance Classically, (n) bits communication are still necessary for an exact solution Quantum mechanically, O(log n) qubits communication are sufficient for an exact solution (It’s a distributed variant of the Deutsch-Jozsa problem … a “constant” vs. “balanced” distinguishing problem) [BCW ’ 98] 17

Classical lower bound (*skipped) Theorem: If S {0, 1}n has the property that, for all x, x′ S, their intersection size is not n/4 then S < 1. 99 n Let some protocol solve restricted equality with k bits comm. ● 2 k conversations of length k ● approximately 2 n/ n input pairs (x, x), where Δ(x) = n/2 Therefore, 2 n/2 k n input pairs (x, x) that yield same conv. C Define S = {x : Δ(x) = n/2 and (x, x) yields conv. C } For any x, x′ S, input pair (x, x′ ) also yields conversation C Therefore, Δ(x, x′) n/2, implying intersection size is not n/4 Theorem implies 2 n/2 k n < 1. 99 n , so k > 0. 007 n [Frankl and Rödl, 1987] 18

Quantum protocol For each x {0, 1}n, define Protocol: 1. Alice sends x to Bob (log(n) qubits) 2. Bob measures state in a basis that includes y Correctness of protocol: If x = y then Bob’s result is definitely y If (x, y) = n/2 then x y = 0, so result is definitely not y Question: How much communication if error prob. ¼ is ok? Answer: just 2 bits are sufficient! 19

Exponential quantum vs. classical separation in bounded-error models : a log(n)-qubit state U: unitary operation (described classically) on log(n) qubits M: two-outcome measurement Output: result of applying M to U O(log n) quantum vs. (n 1/4 / log n) classical communication [R ’ 99] 20

3. Quantum speed-up is not always possible 21

Inner product IP(x, y) = x 1 y 1 + x 2 y 2 + + xn yn mod 2 Classically, (n) bits of communication are required, even for bounded-error protocols Quantum protocols also require (n) communication [KY ’ 95] [CNDT ’ 98] [NS ’ 02] 22

Recall Deutsch’s problem Let f : {0, 1} be of the form f(x) = a 1 x + a 0 mod 2 Given: black box for f Goal: determine a 1 (a 1 = 0 implies “constant”; a 1 = 1 implies “balanced”) Classically, 2 queries are necessary Quantum mechanically, 1 query is sufficient 23

Bernstein-Vazirani problem (multidimensional Deutsch problem) Let f(x 1, x 2, …, xn) = a 1 x 1 + a 2 x 2 + + an xn + a 0 mod 2 Given: 0 x 1 H 0 x 2 H H 0 xn. H 1 b H f H x 1 a 1 H x 2 a 2 H H xn an H b 1 f( x 1, x 2, …, xn) Goal: determine a 1, a 2 , …, an Classically, n +1 queries are necessary Quantum mechanically, 1 query is sufficient 24

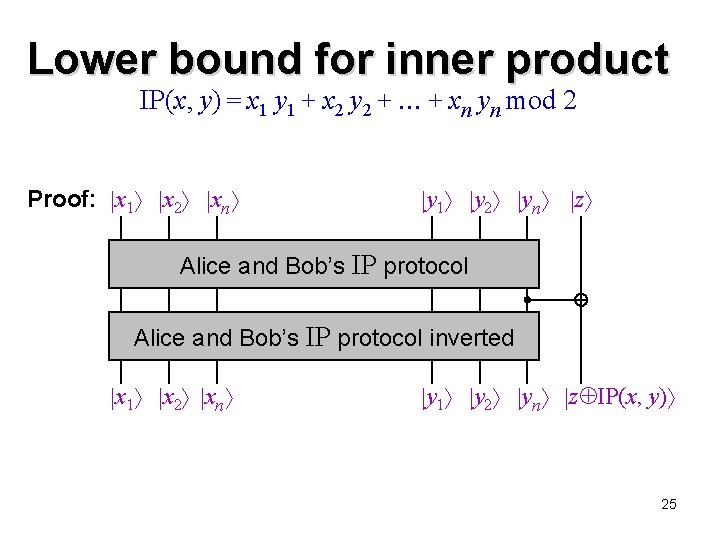
Lower bound for inner product IP(x, y) = x 1 y 1 + x 2 y 2 + + xn yn mod 2 Proof: x 1 x 2 xn y 1 y 2 yn z Alice and Bob’s IP protocol inverted x 1 x 2 xn y 1 y 2 yn z IP(x, y) 25

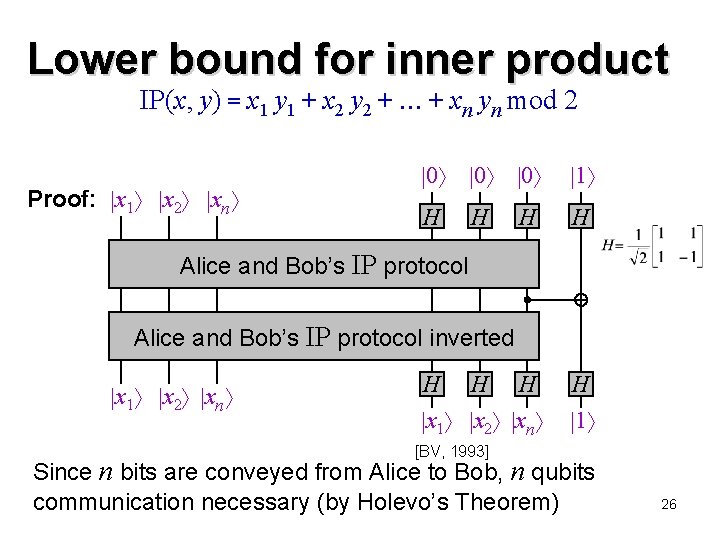
Lower bound for inner product IP(x, y) = x 1 y 1 + x 2 y 2 + + xn yn mod 2 Proof: x 1 x 2 xn 0 0 0 1 H H H x 1 x 2 xn H 1 H Alice and Bob’s IP protocol inverted x 1 x 2 xn [BV, 1993] Since n bits are conveyed from Alice to Bob, n qubits communication necessary (by Holevo’s Theorem) 26

4. Simultaneous messages to a third party 27

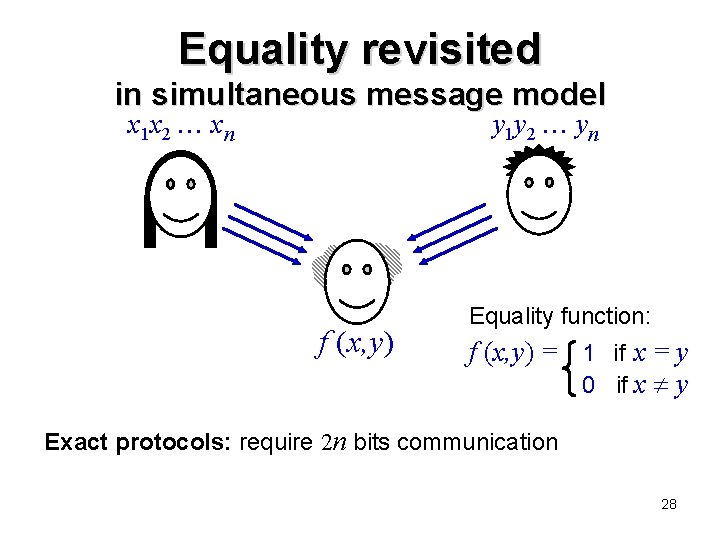
Equality revisited in simultaneous message model x 1 x 2 xn y 1 y 2 yn f (x, y) Equality function: f (x, y) = 1 if x = y 0 if x y Exact protocols: require 2 n bits communication 28

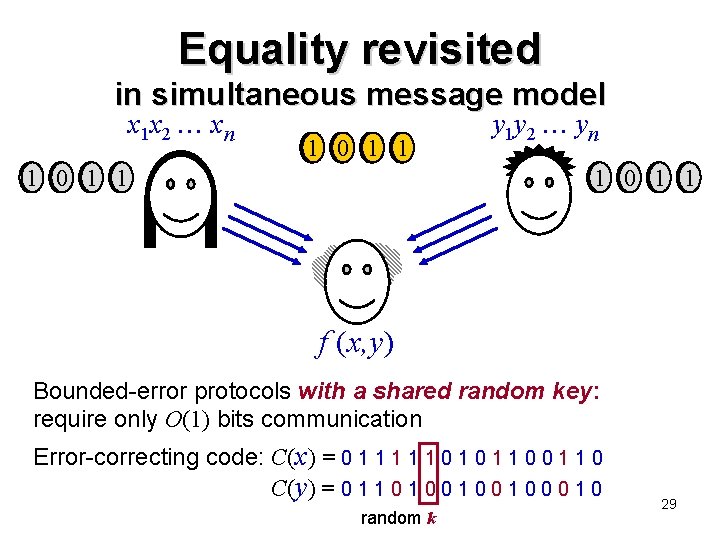
Equality revisited in simultaneous message model x 1 x 2 xn 1 0 1 1 y 1 y 2 yn 1 0 1 1 f (x, y) Bounded-error protocols with a shared random key: require only O(1) bits communication Error-correcting code: C(x) = 0 1 1 1 0 0 1 1 0 C(y) = 0 1 1 0 0 0 1 0 random k 29

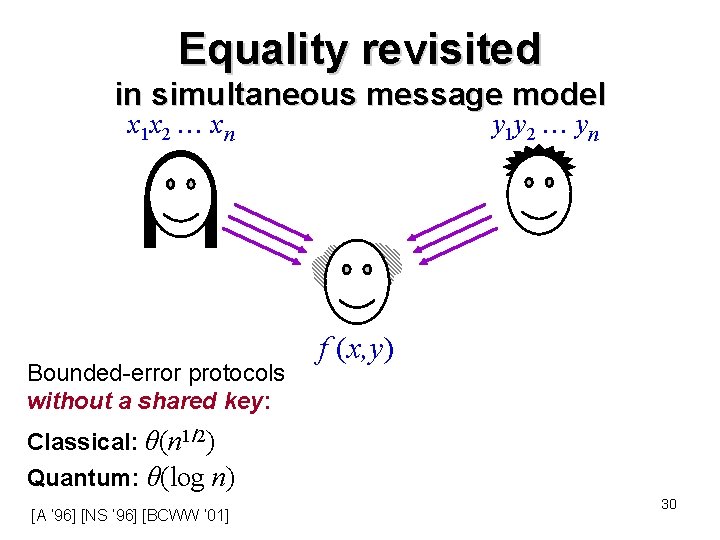
Equality revisited in simultaneous message model x 1 x 2 xn Bounded-error protocols without a shared key: y 1 y 2 yn f (x, y) Classical: θ(n 1/2) Quantum: θ(log n) [A ’ 96] [NS ’ 96] [BCWW ’ 01] 30

Quantum fingerprints Question 1: how many orthogonal states in k qubits? Answer: 2 k Question 2: how many almost orthogonal* states in k qubits? (* where | x y | ≤ ) k Answer: 2 c 2 , for some constant c > 0 Question 3: does this enable k qubits to store c 2 k bits? (In other words, log n + O(1) qubits to store n bits? ) Answer: no … recall Holevo’s Theorem However, it does enable one to check if x = y or x ≠ y by only examining x and y 31

Quantum fingerprints Let 000 , 001 , …, 111 be 2 n states on log n + O(1) qubits such that | x y | ≤ for all x ≠ y Given x y , one can check if x = y or x ≠ y as follows: 0 x y H H if x = y, Pr[output = 0] = 1 ≠ y, Pr[output = 0] = (1+ 2)/2 S W A P Intuition: 0 x y + 1 y x 32

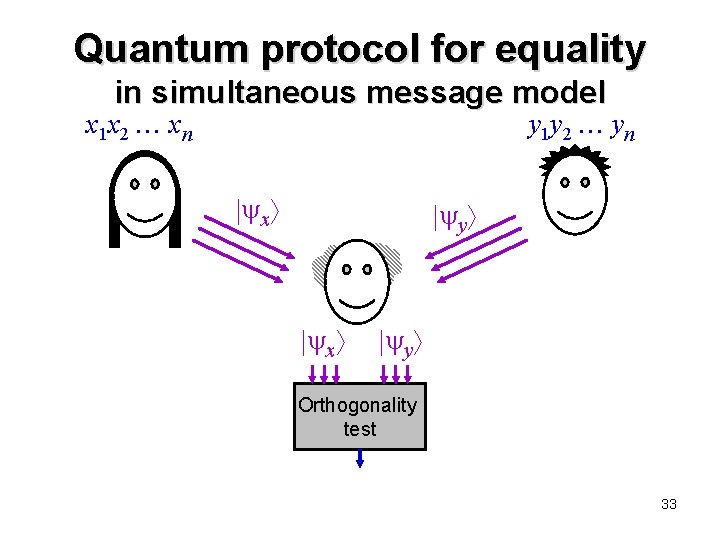
Quantum protocol for equality in simultaneous message model x 1 x 2 xn y 1 y 2 yn x y Orthogonality test 33

5. One-way communication 34

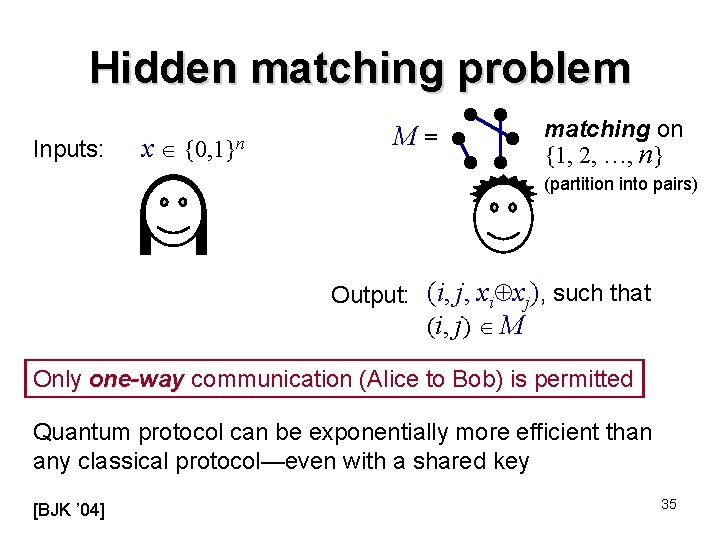
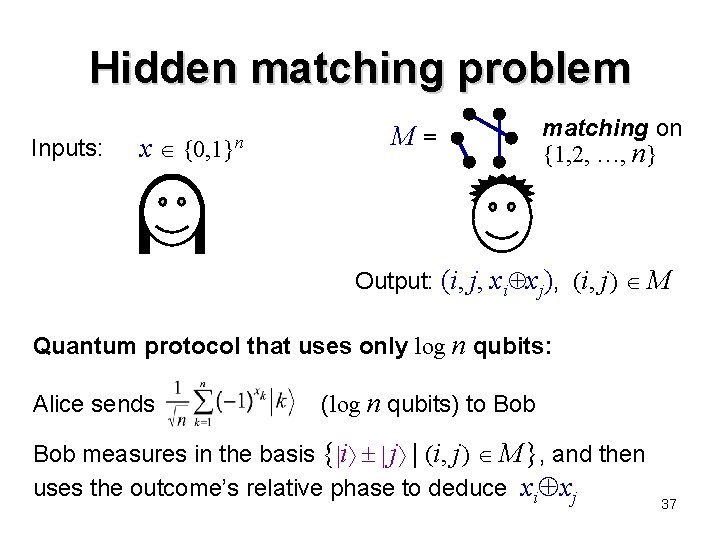
Hidden matching problem Inputs: x {0, 1}n M= matching on {1, 2, …, n} (partition into pairs) Output: (i, j, xi xj), such that (i , j ) M Only one-way communication (Alice to Bob) is permitted Quantum protocol can be exponentially more efficient than any classical protocol—even with a shared key [BJK ’ 04] 35

Hidden matching problem Inputs: x {0, 1}n M= matching on {1, 2, …, n} Output: (i, j, xi xj), (i, j) M Classically, one-way communication is ( n) for bounded-error even with a shared classical key (the proof is omitted here) Intuition: With Alice’s message Bob can repeat his side of the protocol using several edge-disjoint matchings, which yields information about several xi xj bits … 36

Hidden matching problem Inputs: x {0, 1}n M= matching on {1, 2, …, n} Output: (i, j, xi xj), (i, j ) M Quantum protocol that uses only log n qubits: Alice sends (log n qubits) to Bob measures in the basis { i j | (i, j ) M }, and then uses the outcome’s relative phase to deduce xi xj 37

6. Nonlocality revisited 38

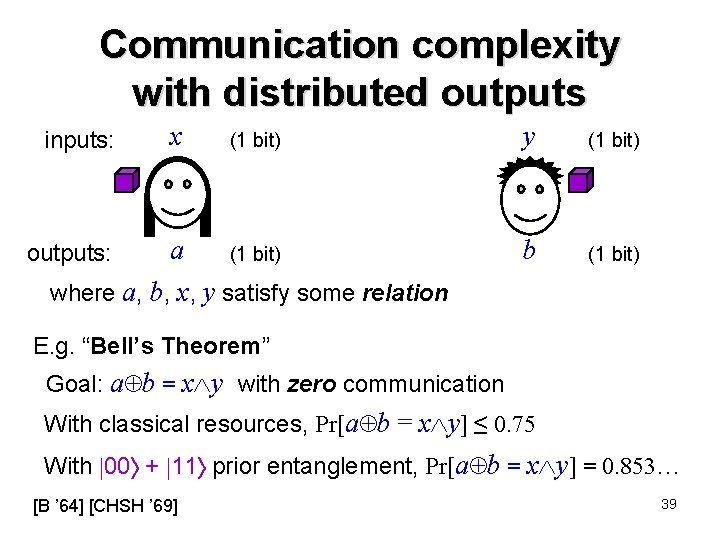
Communication complexity with distributed outputs (1 bit) y (1 bit) a (1 bit) where a, b, x, y satisfy some relation b (1 bit) inputs: x outputs: E. g. “Bell’s Theorem” Goal: a b = x y with zero communication With classical resources, Pr[a b = x y] ≤ 0. 75 With 00 + 11 prior entanglement, Pr[a b = x y] = 0. 853… [B ’ 64] [CHSH ’ 69] 39

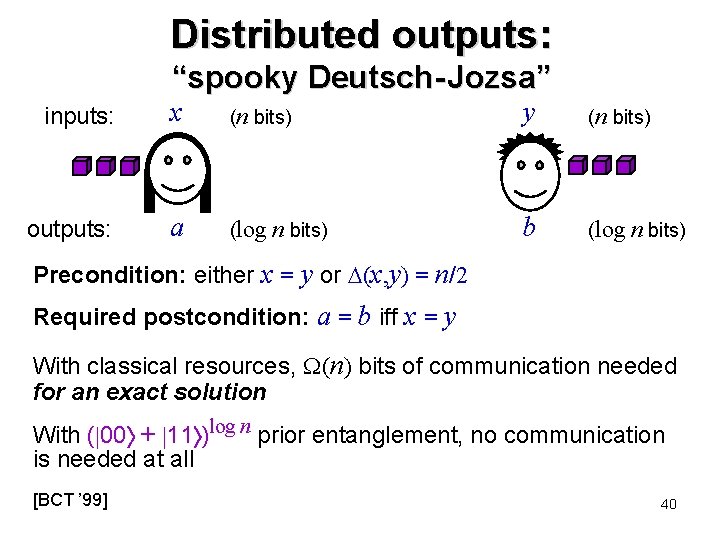
Distributed outputs: “spooky Deutsch- Jozsa” inputs: x (n bits) y (n bits) outputs: a (log n bits) b (log n bits) Precondition: either x = y or (x, y) = n/2 Required postcondition: a = b iff x = y With classical resources, (n) bits of communication needed for an exact solution With ( 00 + 11 )log n prior entanglement, no communication is needed at all [BCT ’ 99] 40

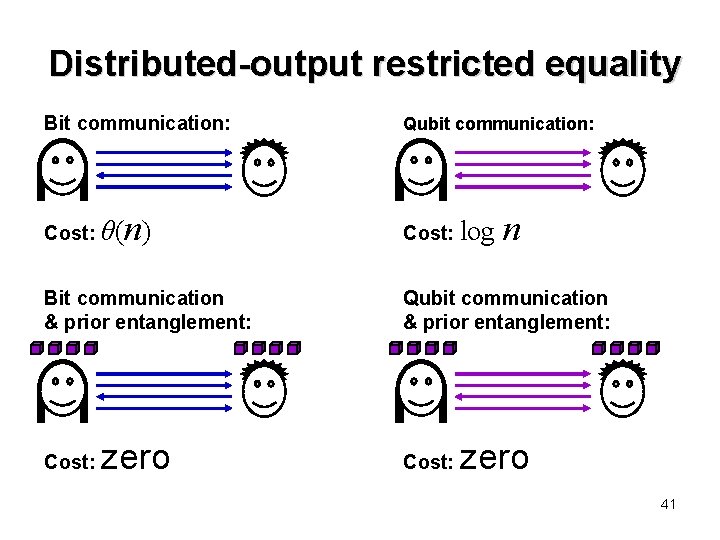
Distributed-output restricted equality Bit communication: Cost: θ( n) Bit communication & prior entanglement: Cost: zero Qubit communication: Cost: log n Qubit communication & prior entanglement: Cost: zero 41

Distributed-output hidden matching Inputs: x {0, 1}n M= matching on {1, 2, …, n} (partition into pairs) Outputs: a {0, 1}log n (b, i, j), such that 1. (i, j) M 2. (a b)·(i j) = xi xj With prior entanglement, no communication necessary; without prior entanglement, one-way communication is ( n), even to achieve success probability ¾ [B ’ 04] 42

Some open problems • Develop some “Killer Apps” • Exponential separation between one-round quantum and multi-round classical? • Are the qubit communication and the prior entanglement models equivalent? • The distributed-output scenario can be viewed as a two-prover interactive proof system, raising questions about their expressive power in a quantum world (may come up on Thursday …) 43

Selected references I • Z. Bar-Yossef, T. S. Jayram, I. Kerenidis, “Exponential separation of quantum and classical one-way communication complexity”, Proceedings of 36 th Annual ACM Symposium on Theory of Computing, pages 128 -137, 2004. • G. Brassard, “Quantum communication complexity”, Foundations of Physics, 33(11): 15931616, 2003. • R. de Wolf, “Quantum communication and complexity”, Theoretical Computer Science, 287(1): 337 -353, 2002. Available at http: //homepages. cwi. nl/~rdewolf/ • G. Brassard, R. Cleve, A. Tapp, “Cost of exactly simulating quantum entanglement with classical communication”, Physical Review Letters, 83(9): 1874 -1877, 1999. • H. Buhrman, R. Cleve, W. van Dam, “Quantum entanglement and communication complexity”, SIAM Journal on Computing, 2000. • H. Buhrman, R. Cleve, A. Wigderson, “Quantum vs. classical communication and computation”, Proceedings of the 30 th Annual ACM Symposium on Theory of Computing, pages 63 -68, 1998. • R. Cleve, H. Buhrman, “Substituting quantum entanglement for communication”, Physical Review A, 56(2): 1201 -1204, 1997. 44

Selected references II • R. Cleve, W. van Dam, P. Høyer, A. Tapp, “Quantum entanglement and the communication complexity of the inner product function”, Lecture Notes in Computer Science, 1509: 61 -74, 1999. • A. Holevo, “Bounds on the quantity of information transmitted by a quantum communication channel”, Problems of Information Transmission, 9: 177 -183, 1973. • B. Kalyanasundaram, G. Schnitger, “The probabilistic communication complexity of set intersection”, Proceedings of 2 nd Annual IEEE Conference on Structure in Complexity Theory, pages 41 -47, 1987. • I. Kremer, Quantum Communication, Master’s thesis, Hebrew University, Computer Science Department, 1995. • R. Raz, “Exponential separation of quantum and classical communication complexity”, Proceedings of 31 st Annual ACM Symposium on Theory of Computing, pages 358 -367, 1999. • A. C. -C. Yao, “Some questions related to distributed computing”, Proceedings of 11 th Annual ACM Symposium on Theory of Computing, pages 209 -213, 1979. • A. C. -C. Yao, “Quantum circuit complexity”, Proceedings of 34 th Annual IEEE Symposium on Foundations of Computer Science, pages 352 -361, 1993. 45

46