Communication Complexity Information Complexity and Applications to Privacy

Communication Complexity, Information Complexity and Applications to Privacy Toniann Pitassi University of Toronto

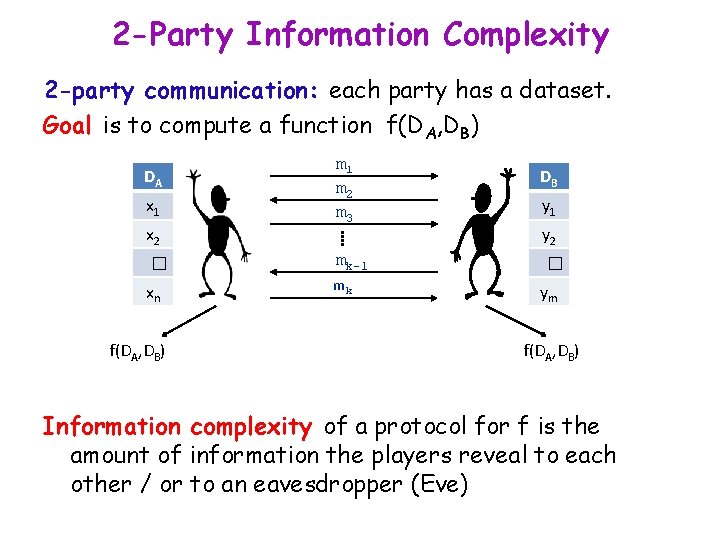
2 -Party Communication Complexity [Yao] 2 -party communication: each party has a dataset. Goal is to compute a function f(DA, DB) DA x 1 x 2 m 1 m 2 m 3 � mk-1 xn mk f(DA, DB) DB y 1 y 2 � ym f(DA, DB) Communication complexity of a protocol for f is the number of bits exchanged between A and B. In this talk, all protocols are assumed to be randomized.

Deterministic Protocols • A deterministic protocol Π specifies: – Function of board contents: • if the protocol is over • if YES, the output • if NO, which player writes next – Function of board contents and input available to player P: • what P writes • Cost of Π = max number of bits written on the board over all inputs

Randomized Protocols • In a randomized protocol Π, what player P writes is also a function of the (private and/or public) random string available to P • Protocol allowed to err with probability ε over choice of random strings • The cost of Π = max number of bits written on the board, over inputs and random strings

Communication Complexity • Focus on randomized communication complexity: CC(F, ε) = the communication cost of computing F with error ε. • A distributional flavor of randomized communication complexity: CC(F, μ, ε) = the communication cost of computing F with error ε with respect to μ. • Yao’s minimax: CC(F, ε)=maxμ CC(F, μ, ε). 5

Stunning variety of applications of CC Lower Bounds 1. 2. 3. 4. 5. 6. 7. 8. Lower Bounds for Streaming Algorithms Data Structure Lower Bounds Proof Complexity Lower Bounds Game Theory Circuit Complexity Lower Bounds Quantum Computation Differential Privacy ……

2 -Party Information Complexity 2 -party communication: each party has a dataset. Goal is to compute a function f(DA, DB) DA x 1 x 2 m 1 m 2 m 3 � mk-1 xn mk f(DA, DB) DB y 1 y 2 � ym f(DA, DB) Information complexity of a protocol for f is the amount of information the players reveal to each other / or to an eavesdropper (Eve)

Information Complexity [Chakrabarti, Shi, Wirth, Yao ‘ 01], [Bar-Yossef, Jayram, Kumar, Sivakumar ‘ 04] Entropy: H(X) = Σx p(x) log (1/p(x) Conditional entropy: H(X|Y) = Σy H(X|Y=y) p(Y=y) Mutual Information: I(X; Y) = H(X) - H(X|Y) External IC: information about XY revealed to Eve ICext (π, μ) = I(XY; π) ICext (f, μ, ε) = maxπ ICext(π, μ) Internal IC: information revealed to Alice and Bob ICint (π, μ) = I(X; π|Y) + I(Y; π|X) ICint (f, μ, ε) = maxπ ICint (π, μ)

Why study information complexity? • Intrinsically interesting quantity • Related to longstanding questions in complexity theory (direct sum conjecture) • Very useful when studying privacy, and quantum computation

Simple Facts about Information Complexity • External information cost is greater than internal: ICext(π, μ) ≥ ICint (π, μ) ICext(π) = I(XY; π) = I(X; π) + I(Y; π | X) ≥ I(X; π|Y) + I(Y; π | X) = ICint (π) • Information complexity lower bounds imply Communication Complexity lower bounds: CC(f, μ, ε) ≥ ICext(f, μ, ε) ≥ ICint (f, μ, ε)

Do CC Lower Bounds imply IC Lower Bounds? (i. e. , CC=IC? ) • For constant-round protocols, IC and CC are basically equal [CSWY, JRS] • Open for general protocols. • Significant step for general case by [BBCR]

Compressing Interactive Communication [Barak, Braverman, Chen, Rao] Theorem 1 For any distribution μ, any C-bit protocol of internal IC I can be simulated by a new protocol using O(√(CI) log. C) bits. Theorem 2 For any product distribution μ, any C-bit protocol of internal IC I can be simulated by a protocol using O(I log. C) bits.

Connection to the Direct Sum Problem Does it take m times the amount of resources to solve m instances? • Direct Sum Question for CC: CC(fm) ≥ m CC(f) for every f and every distribution? - Each copy should have error ε • For search problems, the direct sum problem is equivalent to separating NC 1 from P !

Connection to the Direct Sum Problem, 2 • The direct sum property holds for information complexity: Lemma [Direct Sum for IC]: IC(fm) ≥ m IC(f) • Best general direct sum theorem known for cc: Theorem [Barak, Braverman, Chen, Rao]: CC(fm) ≥ √m CC(f) ignoring polylog factors • The direct sum property for cc is equivalent to IC=CC! Theorem [Braverman, Rao]: IC(f, μ, ε) = limn ∞ CC(Fn, μn, ε)/n

Methods for Proving CC and IC Lower Bounds Jain and Klauck initiated the formal study of CC lower bound methods: all formalizable as solutions to (different) LPs • Discrepancy Method, Smooth Discrepancy Method • Rectangle Bound, Smooth Rectangle Bound • Partition Bound

The Partition Bound [Jain, Klauck] Min Σz, R wz, R ∀ (x, y) Σ R, (x, y) ϵ R wf(x, y), R ≥ 1 -ε ∀ (x, y) ΣR, (x, y) in R Σz wz, R = 1 ∀ z, R w z, R ≥ 0

Relationships The Partition bound is greater than or equal to all known CC lower bounds methods, including: • Discrepancy • Generalized Discrepancy • Rectangle • Smooth Rectangle

All known CC Lower Bound Methods Imply IC Lower Bounds! [Kerenidis, Laplante, Lerays, Roland Xiao ‘ 12] • [KLLR] define the relaxed partition bound. The relaxed partition bound is greater than or equal to all known CC lower bound methods (except the partition bound). • They show that the relaxed Partition bound is equivalent to designing a zero-communication protocol with error exp(-I) • Given a protocol for f with ICint = I, they construct a zero-communication protocol st (i) non-abort probability is exp(-I), and (ii) if it does not abort, it computes f correctly whp

Applications of Information Complexity • Differential Privacy • PAR

Applications of Information Complexity • Differential Privacy • PAR

Differential Privacy: The Basic Scenario [Dwork, Mc. Sherry, Nissim, Smith 06] • Database with rows x 1. . xn • Each row corresponds to an individual in the database • Columns correspond to fields, such as “name”, “zip code”; some fields contain sensitive information. Goal: Compute and release information about a sensitive database without revealing information about any individual Sanitizer Data Output

Differential Privacy [Dwork, Mc. Sherry, Nissim, Smith 2006] Q = space of queries; Y = output space; X = row space Mechanism M: Xn x Q Y is -differentially private if: for all q in Q, for all adjacent x, x’ in Xn, the distributions M(x, q), M(x’, q) are similar: ∀ y in Y, q in Q: e -�� ≤ Pr[M(x, q) =y] Pr[M(x’, q)=y] ≤ eε Note: Randomness is crucial ratio bounded Pr [response] Y

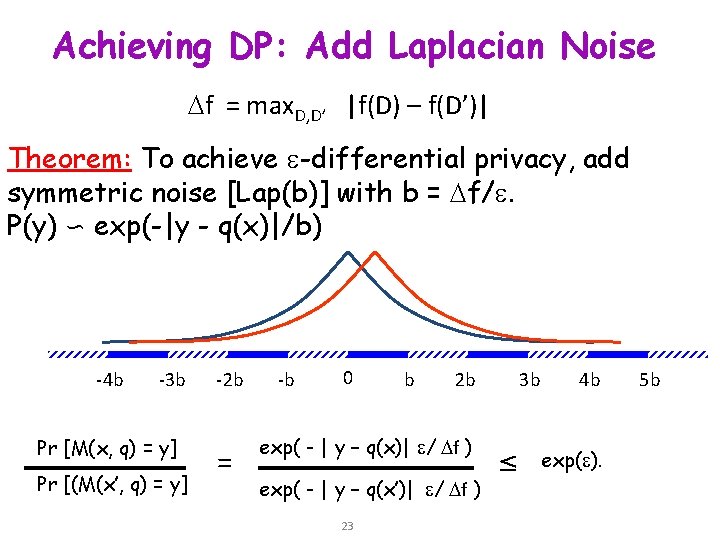
Achieving DP: Add Laplacian Noise f = max. D, D’ |f(D) – f(D’)| Theorem: To achieve -differential privacy, add symmetric noise [Lap(b)] with b = f/. P(y) ∽ exp(-|y - q(x)|/b) -4 b -3 b Pr [M(x, q) = y] Pr [(M(x’, q) = y] -2 b = -b 0 b 2 b exp( - | y – q(x)| / f ) exp( - | y – q(x’)| / f ) 23 3 b ≤ 4 b exp( ). 5 b

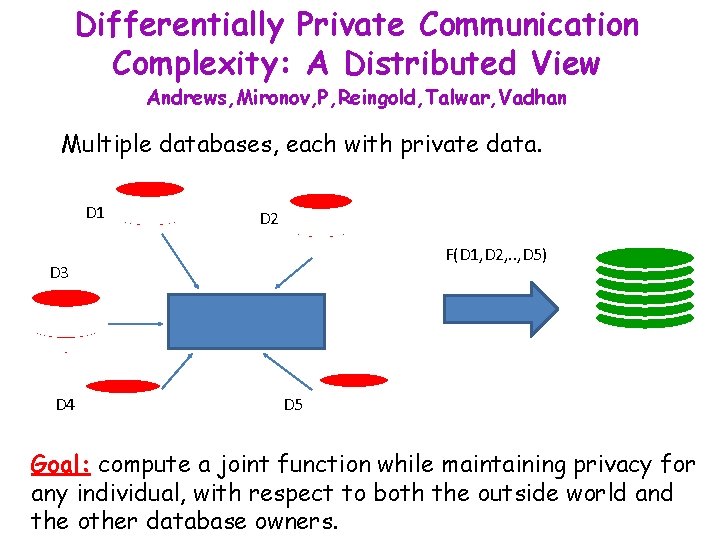
Differentially Private Communication Complexity: A Distributed View Andrews, Mironov, P, Reingold, Talwar, Vadhan Multiple databases, each with private data. D 1 D 2 F(D 1, D 2, . . , D 5) D 3 D 4 D 5 Goal: compute a joint function while maintaining privacy for any individual, with respect to both the outside world and the other database owners.

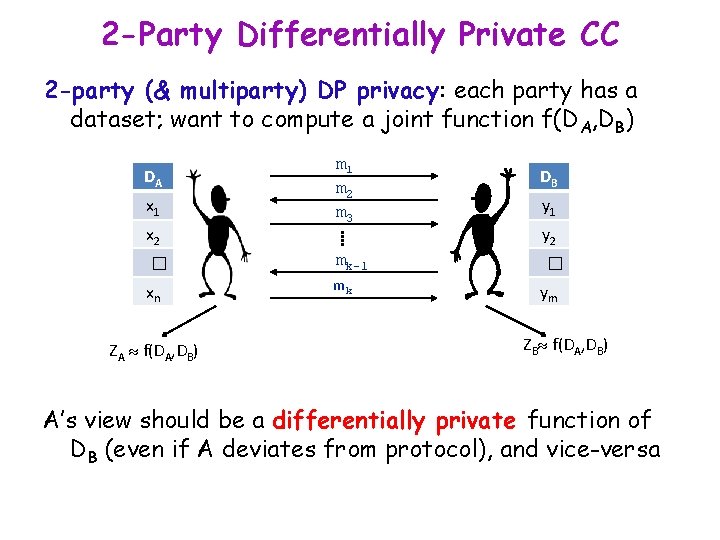
2 -Party Differentially Private CC 2 -party (& multiparty) DP privacy: each party has a dataset; want to compute a joint function f(DA, DB) DA x 1 x 2 m 1 m 2 m 3 � mk-1 xn mk ZA f(DA, DB) DB y 1 y 2 � ym ZB f(DA, DB) A’s view should be a differentially private function of DB (even if A deviates from protocol), and vice-versa

Two-Party Differential Privacy Let P(x, y) be a 2 -party protocol. P is ε-DP if: (1) for all y, for every pair x, x’ that are neighbors, and for every transcript π, Pr[P(x, y) = π ] ≤ exp(ε) Pr[P(x’, y) = π ] (2) symmetrically, for all x, for every pair of neighbors y, y’ and for every transcript π Pr[P(x, y)=π ] ≤ exp(ε) Pr[P(x, y’) = π] • Privacy and accuracy are the important parameters

Examples 1. Ones(x, y) = the number of ones in xy Ones(00001111, 1010) = 8. CC(Ones) = logn. There is a low error DP protocol. 2. Hamming Distance HD(x, y) = the number of positions i where xi ≠ yi. HD(00001111, 1010) = 4 CC(HD)=n. No low error DP protocol Is this a coincidence? Is there a connection between low cc and low-error DP protocols?

Information Cost and DP Protocols [Mc. Gregor, Mironov, P, Reingold, Talwar, Vadhan] Lemma. If π has ε-DP, then for every distribution μ on XY, IC(π, μ, ε) ≤ 3εn Proof sketch: For every z, z’, by ε-DP, exp(-2εn) ≤ Pr[π(z) = π]/Pr[π(z’)=π] ≤ exp(2εn) I(π(Z); X) = H(π(Z)) – H(π(Z) | Z) = Exp{z, π} log[ Pr[π(Z)=π | Z=z] / Pr[π(Z)=π] ] ≤ 2 (log ε) εn DP Partition Theorem. Let P be an ε-DP protocol for a partial function with error at most γ. Then log prtγ(f) ≤ 3 ε n

Lower Bound: Hamming Distance [Mc. Gregor, Mironov, P, Reingold, Talwar, Vadhan] Gap Hamming: GHD(x, y) = 1 if HD(x, y) > n/2 + √n 0 if HD(x, y) < n/2 – √n Theorem. Any ε-DP protocol for Hamming distance must incur an additive error Ω(√n). Note: This lower bound is tight. Proof sketch: [Chakrabarti-Regev 2012] prove: CC(GHD, μ, 1/3) = Ω (n). Proof shows GHD has a smooth rectangle bound of 2Ω(n). By Jain-Klauck, this implies that the partition bound for GHD is at least as large. Thus proof follows by DP Partition Theorem.

Implications of Lower bound for Hamming Distance 1. Separation between ε-DP protocols and computational ε-DP protocols [MPRV]: Hamming distance has an O(1) error computational ε-DP protocol, but any ε-DP protocol has error √n. We also exhibit another function with linear separation. (Any ε-DP protocol has error Ωn) 2. Pan Privacy: Our lower bound for Hamming Distance implies lower bounds for pan-private streaming algorithms

Pan-Private Streaming Model [Dwork, P, Rothblum, Naor, Yekhanin] • Data is a stream of items; each item belongs to a user. Sanitizer sees each item and updates internal state. Generates output at end of the stream (single pass). state Pan-Privacy: For every two adjacent streams, at any single point in time, the internal state (and final output) are differentially private.

What statistics have pan-private algorithms? We give pan-private streaming algorithms for: • Stream density / number of distinct elements • t-cropped mean: mean, over users, of min(t, #appearances) • Fraction of users appearing exactly k times • Fraction of users appearing exactly 0 times modulo k • Fraction of heavy-hitters, users appearing at least k times

Pan Privacy lower bounds via ε-DP lower bounds • Lower Bounds for ε-DP communication protocols imply pan privacy lower bounds for density estimation (via Hamming distance lower bound). • Lower bounds also hold for multi-pass panprivate models • Analogy: 2 -party communication complexity lower bounds imply lower bounds in streaming model.

DP Protocols and Compression So back to Ones(x, y) and HD(x, y). . . is DP the same as compressible? Theorem. [BBCR] (Low Icost implies compression) For every product distribution μ, and protocol P, there exists a protocol Q (β-approximating P) with comm. complexity ∼ Icostμ(P) x polylog(CC(P))/β Corollary. (DP protocols can be compressed) Let P be an ε-DP protocol P. Then there exists a protocol Q of cost 3εn polylog(CC(P))/β and error β. DP almost implies low cc, except for this annoying polylog(CC(P)) factor Moreover, the low cc protocol can often be made DP (if the number of rounds is bounded. )

Differential Privacy and Compression • We have seen that DP protocols have low information cost • By BBCR this implies they can be compressed (and thus have low comm complexity) What about the other direction? Can functions with low cc be made DP? Yes! (with some caveats. . the error is proportional not only to the cc, but also the number of rounds. ) Proof uses the exponential mechanism [MT]

Applications of Information Complexity • Differential Privacy • PAR

Approximate Privacy in Mechanism Design • Traditional goal of mechanism design: Incent agents to reveal private information that is needed to compute optimal results. • Complementary, newly important goal: Enable agents not to reveal private information that is not needed to compute optimal results. • Example (Naor-Pinkas-Sumner, EC ’ 99): It’s undesirable for the auctioneer to learn the winning bid in a 2 nd–price Vickrey auction. 37

Perfect Privacy [Kushilevitz ’ 92] • Protocol P for f is perfectly private iff for all x, x’, y, y’ f(x, y)=f(x’, y’) R(x, y)=R(x’, y’) • f is perfectly privately computable iff M(f) has no forbidden submatrix X 2 x 1 x’ 1 X’ 2 f(x 1, x 2) = f(x’ 1, x’ 2) = a, but f(x 1, x’ 2) ≠ a 38

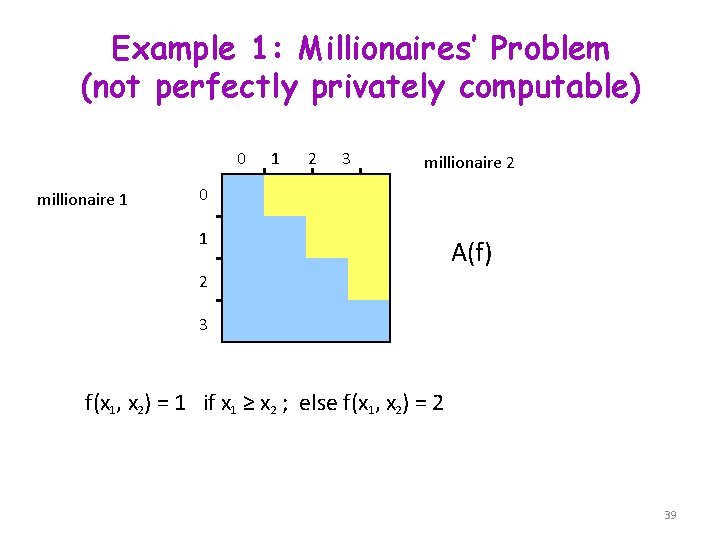
Example 1: Millionaires’ Problem (not perfectly privately computable) 0 millionaire 1 1 2 3 millionaire 2 0 1 A(f) 2 3 f(x 1, x 2) = 1 if x 1 ≥ x 2 ; else f(x 1, x 2) = 2 39

Example 2: Vickrey Auction [Brandt, Sandholm] 0 0 bidder 1 RI (2, 0) 1 1 2 3 bidder 2 2, 0 1, 1 winner price 2, 1 2 1, 2 2, 2 3 1, 3 • The ascending-price, English auction protocol is the unique perfectly private protocol • However the communication cost is exponential !! 40

Worst-case PAR [Feigenbaum, Jaggard, Schapira ‘ 10] • Worst-case privacy approximation ratio of a protocol π for f: PAR(f, π) = max x, y | P(x, y)|/ |R(x, y)|, P(x, y): set of all pairs (x’, y’) st f(x, y)=f’(x’, y’) R(x, y): rectangle containing (x, y) induced by π • Worst-case PAR of f: PAR(f) = min π PAR(f, π) 41

Average-case PAR [Feigenbaum, Jaggard, Schapira ‘ 10] (1) Average-case PAR of π: Avg. PAR 1(f, π) = log E(x, y) |P(x, y)|/|R(x, y)| Avg. PAR 1(f) = minπ Avg. PAR(f, π) (2) Alternative definition: Avg. PAR 2(f, π) = I(XY; π | f) = E(x, y) log |P(x, y)/|R(x, y)| Avg. PAR 2(f) = minπ Avg. PAR 2(f, π) • 1 is log of Expectation, 2 is Expectation of log. • For boolean functions, Avg. PAR 2(f) is basically the same as Icost(f) (differs by at most 1). 42

New Results [Ada, Chattopadhyay, Cook, Fontes, P ‘ 12] (1) Using the fact that Avg. PAR 1 ≥ Avg. PAR 2, together with known IC lower bounds: Theorem Avg. PAR 2 of set intersection is Ω(n) (2) We prove strong tradeoffs for both worst-case PAR and avg. PAR for Vickrey auctions. (3) Using compression [BBCR], it follows that any deterministic, low Avg. PAR 1 protocols can be compressed. Thus binary search protocol for millionaires implies a polylogn randomized protocol. 43

Important Open Questions • IC=CC? • IC in the multiparty NOF setting • IC lower bounds for search problems Very important for proof complexity and circuit complexity • Other applications of IC Data structures? Game Theory?

Thanks!