Principal Component Analysis Canonical Correlation Cluster Analysis Xuhua

Principal Component Analysis Canonical Correlation Cluster Analysis Xuhua Xia xxia@uottawa. ca http: //dambe. bio. uottawa. ca

Multivariate statistics • • PCA: principal component analysis Canonical correlation Cluster analysis. . . Xuhua Xia Slide 2

PCA • Given a set of variables x 1, x 2, …, xn, – find a set of coefficients a 11, a 12, …, a 1 n, so that PC 1 = a 11 x 1 + a 12 x 2 + …+ a 1 nxn has the maximum variance (v 1) subject to the constraint that a 1 is a unit vector, i. e. , sqrt(a 112+ a 122 …+ a 1 n 2) = 1 – find a 2 nd set of coefficients a 2 so that PC 2 has the maximum variance (v 2) subject to the unit vector constraint and the additional constraint that a 2 is orthogonal to a 1 – find 3 rd, 4 th, … nth set of coefficients so that PC 3, PC 4, … have the maximum variance (v 3, v 4, …) subject to the unit vector constraint and that ai is orthogonal to all ai-1 vectors. – It turns out that v 1, v 2, … are eigenvalues and a 1, a 2, … are eigenvectors of the variance-covariance matrix of x 1, x 2, …, xn (or of the correlation matrix if x 1, x 2, …, xn are standardized) • Demonstrate how to find the eigenvalues, eigenvectors, and PC_Scores manually in EXCEL Slide 3

Toy Datasets X 1 -1. 264911064 -0. 632455532 0 0. 632455532 1. 264911064 X 2 -1. 788854382 -0. 894427191 0 0. 894427191 1. 788854382 X 1 1. 31832344 2. 341993124 1. 913119064 3. 00557377 4. 183120958 X 2 1. 064630266 2. 921219905 2. 304482133 2. 691546491 3. 897404623 To demonstrate the physical principles involved in forming a rainbow, it is not necessary to create a rainbow spanning the sky – a small one is sufficient. --C. C. Li Xuhua Xia Slide 4

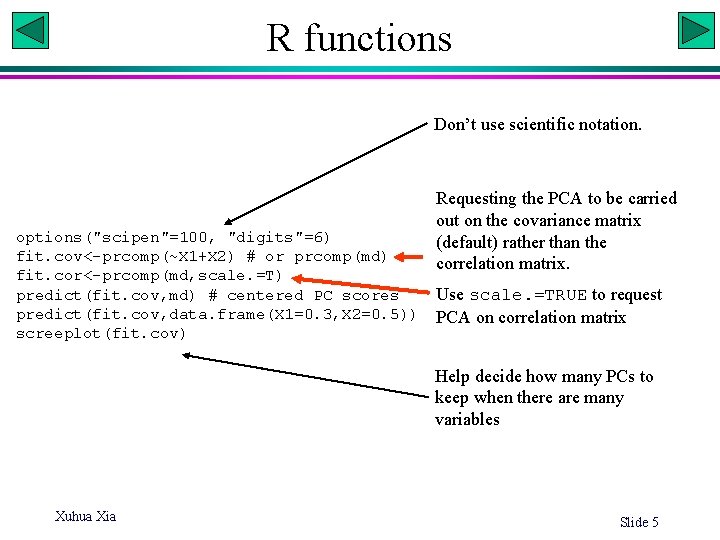
R functions Don’t use scientific notation. options("scipen"=100, "digits"=6) fit. cov<-prcomp(~X 1+X 2) # or prcomp(md) fit. cor<-prcomp(md, scale. =T) predict(fit. cov, md) # centered PC scores predict(fit. cov, data. frame(X 1=0. 3, X 2=0. 5)) screeplot(fit. cov) Requesting the PCA to be carried out on the covariance matrix (default) rather than the correlation matrix. Use scale. =TRUE to request PCA on correlation matrix Help decide how many PCs to keep when there are many variables Xuhua Xia Slide 5

prcomp Output Standard deviations: [1] 1. 7320714226 0. 0000440773 Rotation: PC 1 PC 2 X 1 0. 577347 0. 816499 X 2 0. 816499 -0. 577347 [1, ] [2, ] [3, ] [4, ] [5, ] better to output in variance (eigenvalue) accounted for by each PC eigenvectors: PC 1 = 0. 57735 X 1+0. 81650 X 2 PC 1 PC 2 -2. 19092 0. 0000278767 -1. 09545 -0. 0000557540 Principal component scores, generated by 0. 0000000000 as. matrix(md) %*% as. matrix(fit$rotation) 1. 09545 0. 0000557540 Centered ones is obtained by fit$x 2. 19092 -0. 0000278767 Xuhua Xia Slide 7

PCA on correlation matrix (scale=T) Standard deviations: [1] 1. 4142135619 0. 0000381717 Rotation: PC 1 PC 2 X 1 0. 707107 X 2 0. 707107 -0. 707107 PC 1 PC 2 [1, ] -1. 788850 0. 0000241421 [2, ] -0. 894435 -0. 0000482837 [3, ] 0. 0000000000 [4, ] 0. 894435 0. 0000482837 [5, ] 1. 788850 -0. 0000241421 Xuhua Xia Slide 8

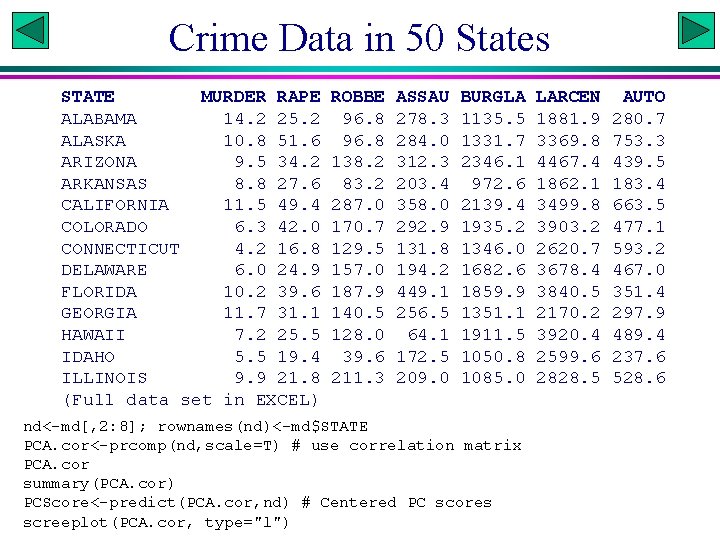
Crime Data in 50 States STATE MURDER RAPE ALABAMA 14. 2 25. 2 ALASKA 10. 8 51. 6 ARIZONA 9. 5 34. 2 ARKANSAS 8. 8 27. 6 CALIFORNIA 11. 5 49. 4 COLORADO 6. 3 42. 0 CONNECTICUT 4. 2 16. 8 DELAWARE 6. 0 24. 9 FLORIDA 10. 2 39. 6 GEORGIA 11. 7 31. 1 HAWAII 7. 2 25. 5 IDAHO 5. 5 19. 4 ILLINOIS 9. 9 21. 8 (Full data set in EXCEL) ROBBE 96. 8 138. 2 83. 2 287. 0 170. 7 129. 5 157. 0 187. 9 140. 5 128. 0 39. 6 211. 3 ASSAU 278. 3 284. 0 312. 3 203. 4 358. 0 292. 9 131. 8 194. 2 449. 1 256. 5 64. 1 172. 5 209. 0 BURGLA 1135. 5 1331. 7 2346. 1 972. 6 2139. 4 1935. 2 1346. 0 1682. 6 1859. 9 1351. 1 1911. 5 1050. 8 1085. 0 nd<-md[, 2: 8]; rownames(nd)<-md$STATE PCA. cor<-prcomp(nd, scale=T) # use correlation matrix PCA. cor summary(PCA. cor) PCScore<-predict(PCA. cor, nd) # Centered PC scores screeplot(PCA. cor, type="l") LARCEN 1881. 9 3369. 8 4467. 4 1862. 1 3499. 8 3903. 2 2620. 7 3678. 4 3840. 5 2170. 2 3920. 4 2599. 6 2828. 5 AUTO 280. 7 753. 3 439. 5 183. 4 663. 5 477. 1 593. 2 467. 0 351. 4 297. 9 489. 4 237. 6 528. 6

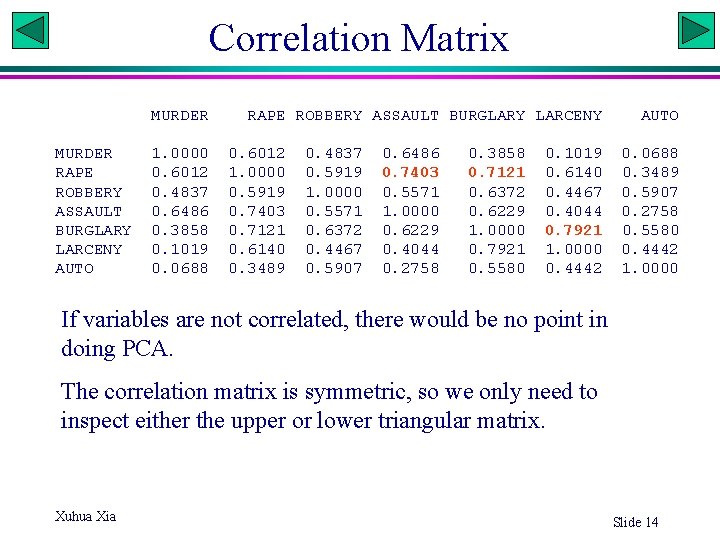
Correlation Matrix MURDER RAPE ROBBERY ASSAULT BURGLARY LARCENY AUTO 1. 0000 0. 6012 0. 4837 0. 6486 0. 3858 0. 1019 0. 0688 RAPE ROBBERY ASSAULT BURGLARY LARCENY 0. 6012 1. 0000 0. 5919 0. 7403 0. 7121 0. 6140 0. 3489 0. 4837 0. 5919 1. 0000 0. 5571 0. 6372 0. 4467 0. 5907 0. 6486 0. 7403 0. 5571 1. 0000 0. 6229 0. 4044 0. 2758 0. 3858 0. 7121 0. 6372 0. 6229 1. 0000 0. 7921 0. 5580 0. 1019 0. 6140 0. 4467 0. 4044 0. 7921 1. 0000 0. 4442 AUTO 0. 0688 0. 3489 0. 5907 0. 2758 0. 5580 0. 4442 1. 0000 If variables are not correlated, there would be no point in doing PCA. The correlation matrix is symmetric, so we only need to inspect either the upper or lower triangular matrix. Xuhua Xia Slide 14

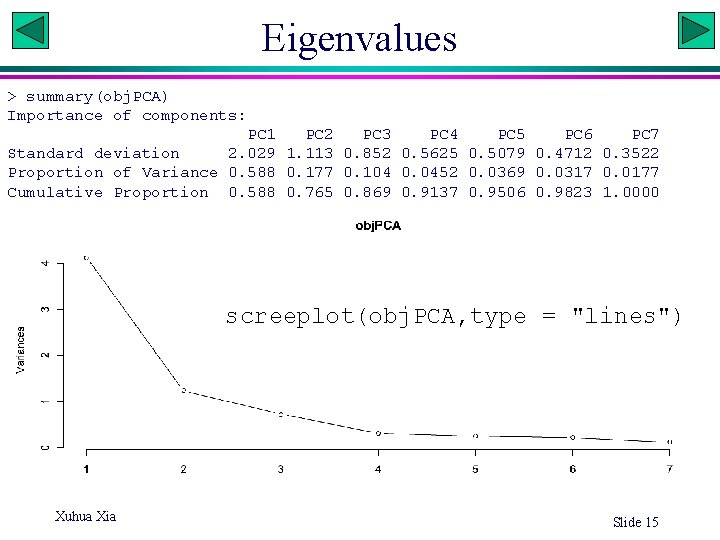
Eigenvalues > summary(obj. PCA) Importance of components: PC 1 PC 2 PC 3 PC 4 PC 5 PC 6 PC 7 Standard deviation 2. 029 1. 113 0. 852 0. 5625 0. 5079 0. 4712 0. 3522 Proportion of Variance 0. 588 0. 177 0. 104 0. 0452 0. 0369 0. 0317 0. 0177 Cumulative Proportion 0. 588 0. 765 0. 869 0. 9137 0. 9506 0. 9823 1. 0000 screeplot(obj. PCA, type = "lines") Xuhua Xia Slide 15

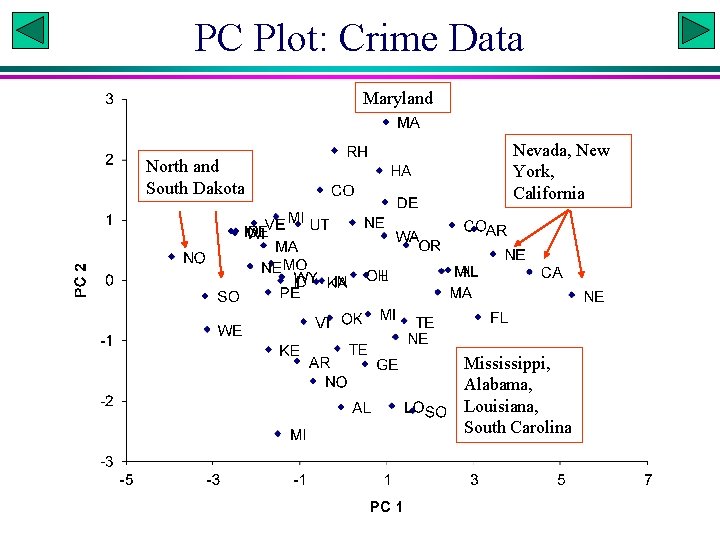
Eigenvectors PC 1 PC 2 PC 3 PC 4 PC 5 PC 6 PC 7 MURDER -0. 3003 -0. 62918 0. 17824 -0. 23216 0. 53810 0. 25912 0. 267589 RAPE -0. 4318 -0. 16944 -0. 24421 0. 06219 0. 18848 -0. 77327 -0. 296490 ROBBE -0. 3969 0. 04224 0. 49588 -0. 55793 -0. 52002 -0. 11439 -0. 003902 ASSAU -0. 3966 -0. 34353 -0. 06953 0. 62984 -0. 50660 0. 17235 0. 191751 BURGLA -0. 4402 0. 20334 -0. 20990 -0. 05757 0. 10101 0. 53599 -0. 648117 LARCEN -0. 3574 0. 40233 -0. 53922 -0. 23491 0. 03008 0. 03941 0. 601688 AUTO -0. 2952 0. 50241 0. 56837 0. 41922 0. 36980 -0. 05729 0. 147044 • Do these eigenvectors mean anything? – All crimes are negatively correlated with the first eigenvector, which is therefore interpreted as a measure of overall safety. – The 2 nd eigenvector has positive loadings on AUTO, LARCENY and ROBBERY and negative loadings on MURDER, ASSAULT and RAPE. It is interpreted to measure the preponderance of property crime over violent crime…. . . Xuhua Xia Slide 16

PC Plot: Crime Data Maryland North and South Dakota Nevada, New York, California Mississippi, Alabama, Louisiana, South Carolina

Multivariate statistics • • PCA: principal component analysis Canonical correlation Cluster analysis. . . Xuhua Xia Slide 18

Correlation • Simple correlation – between two variables • Multiple and Partial correlations – between one variable and a set of other variables • Canonical Correlation – between two sets of variables each containing more than one variable. • Simple and multiple correlations are special cases of canonical correlation. Xuhua Xia Partial: between X and Y with Z being controlled for Multiple: x 1 on x 2 and x 3 Slide 19

Review of correlation X 1 1 1 2 2 2 3 3 4 4 4 5 5 6 6 Z 4 5 6 3 4 5 6 5 3 4 5 6 3 4 5 2 3 4 5 1 2 3 4 Xuhua Xia Y 14. 0000 17. 9087 16. 3255 14. 4441 15. 2952 19. 1587 16. 0299 17. 0000 14. 7556 17. 6823 20. 5301 21. 6408 15. 0903 18. 1603 22. 2471 14. 4450 16. 5554 21. 0047 22. 0000 19. 0000 18. 1863 21. 0000 Compute Pearson correlation coefficients between X and Z, X and Y and Z and Y. Compute partial correlation coefficient between X and Y, controlling for Z (i. e. , the correlation coefficient between X and Y when Z is held constant), by using the equation in the previous slide. Run R to verify your calculation: #install. packages("ggm") library(ggm) md<-read. table("XYZ. txt", header=T) cor(md) s<-var(md) parcor(s) # or parcor(md)) # install. packages("psych") library(psych) smc(s) # squared multiple correlation Slide 20

Data for canonical correlation # First three variables: physical # Last three variables: exercise # Middle-aged men weight waist pulse chins 191 36 50 5 193 38 58 12 189 35 46 13 211 38 56 8 176 31 74 15 169 34 50 17 154 34 64 14 193 36 46 6 176 37 54 4 156 33 54 15 189 37 52 2 162 35 62 12 182 36 56 4 167 34 60 6 154 30 56 17 166 33 52 13 247 46 50 1 202 37 62 12 157 32 52 11 138 33 68 2 situps 162 101 145 151 200 120 215 170 160 215 130 145 141 155 251 210 50 120 230 150 jumps 60 101 58 38 40 38 105 31 25 73 60 37 42 40 250 115 50 120 80 43 Use EXCEL to manually calculate the first canonical correlation Slide 21

Canonical correlation (cc) install. packages("ggplot 2") install. packages("Ggally") install. packages("CCA") install. packages("CCP") require(ggplot 2) require(GGally) require(CCA) require(CCP) phys<-md[, 1: 3] exer<-md[, 4: 6] matcor(phys, exer) cc 1<-cc(phys, exer) cc 1 http: //www. ats. ucla. edu/stat/r/dae/canonical. htm

cc output [1] 0. 87857805 0. 26499182 0. 06266112 canonical correlations $xcoef [, 1] [, 2] [, 3] weight 0. 007691932 0. 08206036 -0. 01089895 waist -0. 352367502 -0. 46672576 0. 12741976 pulse -0. 016888712 0. 04500996 0. 14113157 raw canonical coefficients matrices: U and V phys*U: raw canonical variates for phys $ycoef [, 1] [, 2] [, 3] chins 0. 063996632 0. 19132168 0. 116137756 situps 0. 017876736 -0. 01743903 0. 001201433 jumps -0. 002949483 0. 00494516 -0. 022700322 exer*V: raw canonical variates for exer $scores$xscores: standardized canonical variates.

standardized canonical variates $scores$xscores [, 1] [1, ] -0. 06587452 [2, ] -0. 89033536 [3, ] 0. 33866397 [4, ] -0. 71810315 [5, ] 1. 17525491 [6, ] 0. 46963797 [7, ] 0. 11781701 [8, ] 0. 01706419 [9, ] -0. 60117586 [10, ] 0. 65445550 [11, ] -0. 46740331 [12, ] -0. 13923760 [13, ] -0. 23643419 [14, ] 0. 28536698 [15, ] 1. 66239672 [16, ] 0. 76515225 [17, ] -3. 15880133 [18, ] -0. 53629531 [19, ] 1. 04829236 [20, ] 0. 27955875 [, 2] 0. 39294336 -0. 01630780 0. 51550858 1. 37075870 2. 57590579 -0. 47893295 -1. 07969890 0. 37702424 -1. 12464792 -0. 89895199 -0. 14788320 -0. 97996173 -0. 07554011 -0. 19295410 0. 42712450 -0. 16836835 0. 32106568 1. 36900100 -0. 44018579 -1. 74589901 [, 3] -0. 90048466 0. 46160952 -1. 57063280 -0. 01683463 2. 01305832 -0. 91554740 1. 22377873 -1. 48680882 -0. 04505445 -0. 33675460 -0. 46900387 0. 98174380 0. 04439525 0. 51756617 -0. 41495287 -0. 72800719 -0. 23662794 0. 80062552 -0. 75733645 1. 83526836 $scores$yscores [, 1] [1, ] -0. 23742244 [2, ] -1. 00085572 [3, ] -0. 02345494 [4, ] -0. 17718803 [5, ] 1. 14084951 [6, ] -0. 15539717 [7, ] 1. 15328755 [8, ] 0. 05512308 [9, ] -0. 23394065 [10, ] 1. 31166763 [11, ] -1. 00146790 [12, ] -0. 02551244 [13, ] -0. 62373985 [14, ] -0. 23957331 [15, ] 1. 56116497 [16, ] 0. 97041241 [17, ] -2. 46610861 [18, ] -0. 71723790 [19, ] 1. 30318577 [20, ] -0. 59379197 [, 2] -0. 91888370 1. 68690015 0. 89826285 -0. 26188291 0. 23274696 2. 00062200 0. 10127530 -1. 01048386 -1. 24840794 0. 13435186 -0. 93479995 0. 60309281 -0. 83299874 -0. 70439205 0. 76448365 0. 04660035 0. 21954878 1. 44951672 -0. 85790412 -1. 36764817 [, 3] -0. 28185833 -0. 47289464 0. 67222000 0. 55274626 1. 37918010 1. 56074166 -0. 19445711 0. 50220023 0. 39411232 0. 64809096 -0. 66871744 1. 03278901 -0. 01462037 0. 27987584 -3. 09433899 -0. 54360525 -0. 65396658 -0. 88137354 0. 04265917 -0. 25878331

Canonical structure: Correlations $scores$corr. X. xscores [, 1] [, 2] [, 3] weight -0. 8028458 0. 53345479 -0. 2662041 waist -0. 9871691 0. 07372001 -0. 1416419 pulse 0. 2061478 0. 10981908 0. 9723389 correlation between phys variables with CVs_U $scores$corr. Y. xscores [, 1] [, 2] [, 3] chins 0. 6101751 0. 18985890 0. 004125743 situps 0. 8442193 -0. 05748754 -0. 010784582 jumps 0. 3638095 0. 09727830 -0. 052192182 correlation between exer variables with CVs_U $scores$corr. X. yscores [, 1] [, 2] [, 3] weight -0. 7053627 0. 14136116 -0. 016680651 waist -0. 8673051 0. 01953520 -0. 008875444 pulse 0. 1811170 0. 02910116 0. 060927845 correlation between phys variables with CVs_V $scores$corr. Y. yscores [, 1] [, 2] [, 3] chins 0. 6945030 0. 7164708 0. 06584216 situps 0. 9608928 -0. 2169408 -0. 17210961 jumps 0. 4140890 0. 3670993 -0. 83292764 correlation between exer variables with CVs_V

Significance: p. asym in CCP v. Cancor<-cc 1$cor # p. asym(rho, N, p, q, tstat = "Wilks|Hotelling|Pillai|Roy") res<-p. asym(v. Cancor, length(md$weight), 3, 3, tstat = "Wilks") Wilks' Lambda, using F-approximation (Rao's F): stat approx df 1 df 2 p. value At least one cancor significant? 1 to 3: 0. 2112505 3. 4003788 9 34. 22293 0. 004421278 Significant relationship after excluding 2 to 3: 0. 9261286 0. 2933756 4 30. 00000 0. 879945478 cancor 1? 3 to 3: 0. 9960736 0. 0630703 1 16. 00000 0. 804904236 Significant relationship after excluding plt. asym(res, rhostart=1) plt. asym(res, rhostart=2) plt. asym(res, rhostart=3) cancor 1 and 2?

Multivariate statistics • • PCA: principal component analysis Canonical correlation Cluster analysis. . . Xuhua Xia Slide 27

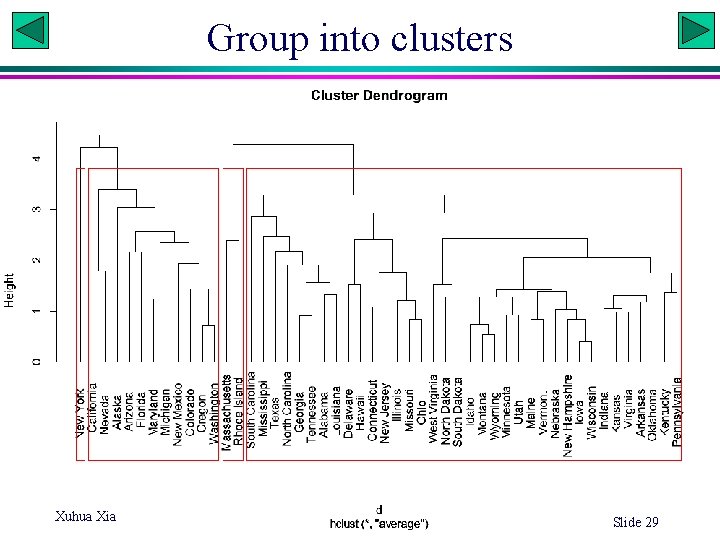
Cluster analysis # Use US crime data nd<-scale(md[, 2: 8]) # nd<-md[, -1] rownames(nd)<-md$STATE d<-dist(nd, method="euclidean") # other distances: , "maximum|manhattan|Canberra|binary|minkowski" hc<-hclust(d, method="average") # default is average linkage (UPGMA) plot(hc, hang=-1) # hang=-1: scale tree with branch length rect. hclust(hc, k=4, border="red") # export tree in Newick format library(ape) class(hc) # must be hclust class my_tree <- as. phylo(hc) write. tree(phy=my_tree, file="clipboard") Slide 28

Group into clusters Xuhua Xia Slide 29

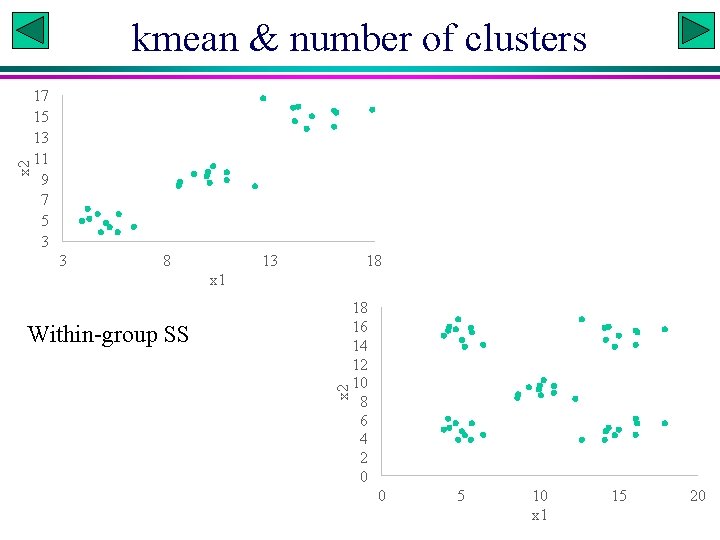
x 2 kmean & number of clusters 17 15 13 11 9 7 5 3 3 8 13 18 x 1 x 2 Within-group SS 18 16 14 12 10 8 6 4 2 0 0 5 10 x 1 15 20

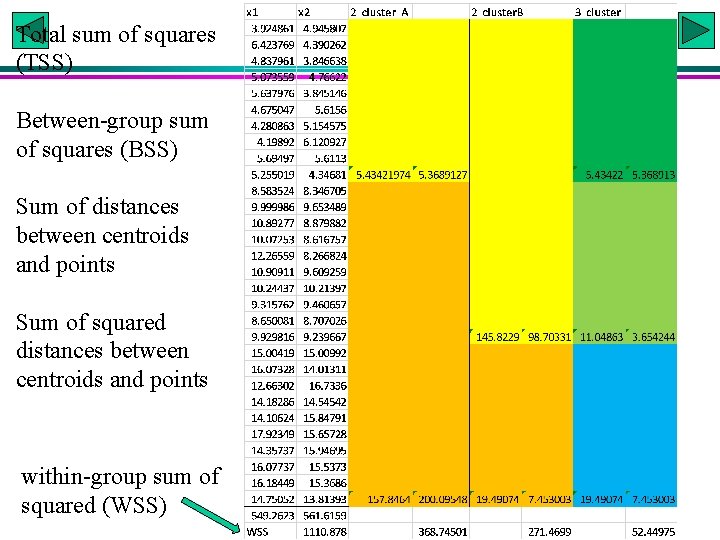
Total sum of squares (TSS) Between-group sum of squares (BSS) Sum of distances between centroids and points Sum of squared distances between centroids and points within-group sum of squared (WSS)

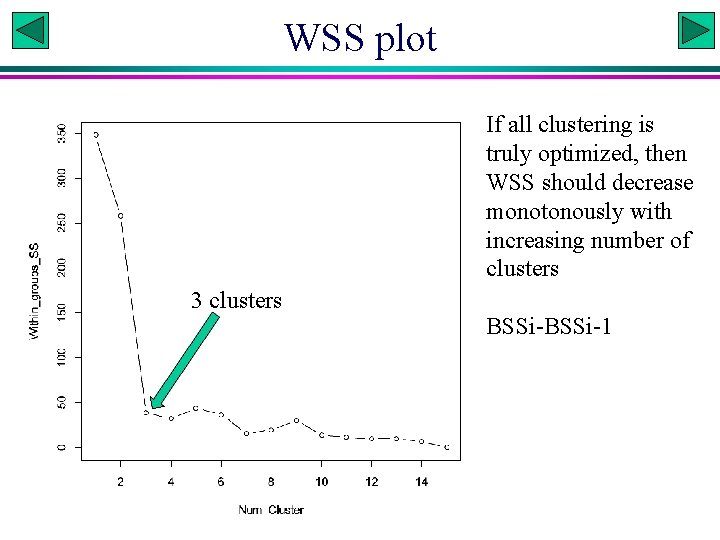
WSS plot If all clustering is truly optimized, then WSS should decrease monotonously with increasing number of clusters 3 clusters BSSi-1

Determining number of clusters (k) # Rationale: plot within-cluster sum of squares over k, with k=2: 15 # wss: within-group sum of squares # apply(md, 1|2, var) 1|2: variables in rows|column # sum(apply(md, 2, var)): sum of variance # DF*var = SS total. WSS <- (nrow(md)-1)*sum(apply(md, 2, var)) # kmeans clustering with 2, 3, …, 15 clusters and compute wss for each WSS<-rep(0, 15) for (i in 1: 15) WSS[i] <- sum(kmeans(md, centers=i)$withinss) num. Cluster<-1: 15 plot(num. Cluster, WSS, type="b", xlab="Num_Cluster", ylab="Within_groups_SS") # Necessary to do this multiple times because of the heuristic nature of the # clustering algorithms. Check WSS[i] values # K-Means Cluster Analysis fit <- kmeans(md, 5) # 5 cluster solution, $cluster, $centers, $totss, $withinss, # $betweenss fit. Array<-array(list(), 10) MSS<-rep(0, 10) for(i in 1: 10) { fit. Array[[i]]<-as. list(fit. Array[[i]]) fit. Array[[i]] <- kmeans(md, 5) # 5 cluster solution MSS[i]<-100*fit. Array[[i]]$betweenss/fit. Array[[i]]$totss } Xuhua Xia Slide 33